一种应用于超声波测量的混频检相方法*

宋 威丁喜波*刘国宏

(1.哈尔滨理工大学测控技术与仪器省高校重点实验室,黑龙江 哈尔滨 150080；2.中国石化胜利油田分公司东辛采油厂,山东 东营 257000)

随着超声波技术的不断发展,其在测量领域的应用得到广泛开发,例如超声波流量计、超声温度计、以及各种应用于气体测量的超声检测仪等。超声波测量常用的相位差法是提高精度的重要手段[1]。因此,对相位检测技术的研究具有重要意义。

文献[2]对被测信号进行奇异值分解构成汉克尔(Hankel)矩阵,利用奇异值降序排列规律进行相应处理后,使用Hilbert 变换法进行相位差计算,信号处理过程运算复杂且容易引入不必要的噪声信息。文献[3]设计了基于双中频超外差式结构的反馈系统,将信号进行变频后测量相位差,结构设计复杂,被测信号相位稳定性差。文献[4]采用PLC 控制系统,利用中断方式对高速计数器进行复位和读取操作,并通过相应的算法获取相位差值,但被测信号频率受采样频率限制。文献[5]对科氏流量计系统进行数学建模,结合最小二乘法和曲线拟合的思想改进了相位检测方法,但数据处理运算复杂,测量精度依赖数学模型。文献[6]设计了基于混频算法的数字信号处理系统,通过在固定采样频率下对经过调理电路、模/数(A/D)转换电路的信号进行混频,计算得出相位差值,但需要实时跟踪信号的频率,且信号频率与传感器的瞬时频率不同步时存在误差。文献[7]提出了基于相关原理的相位差测量改进算法,通过设计产生两路移相90°参考信号与原信号进行相关运算获得相位信息,但当信号频率未知时,对于两路参考信号的获取十分复杂,需要先通过陷波器或者离散频谱校正的方法获取信号频率,再进行波形变换。文献[8]提出了一种非半周期采样信号相位差估计的相位校正相关法,通过相位校正互相关信号和频率估计值获得采样信号的相位差估计值,但互相关信号的获取过程十分复杂,需要信号时移、互相关、误差项相消等技术进行处理,数据运算量特别大。

根据现有的相位差检测技术,提出了一种基于相关性原理的混频检相方法,利用混频原理将被测信号频率进行转换,经过滤波整形电路后由检相电路实现相位差的测量。根据系统结构原理,完成了混频检相器的硬件电路,通过仿真和电路的实测说明了采用混频原理进行频率的转换能够适应高频超声信号环境下的测量,验证了所提出的混频检相方法的可行性。

1 原理分析

混频检相器设计如图1 所示,主要由将高频信号转化为低频信号的混频电路,滤除高频保留低频的低通滤波电路,将正弦信号转换为方波信号的整形电路,获得被测信号相位差的检相电路组成。频率为f的被测信号和频率为f＋Δf的参比信号经过混频检相器调制后得到相位差信息。

根据混频器原理可知,两路被测信号通过与给定的信号进行混频操作,不会改变信号的相位特性,只是进行频谱的转换[2-11],通过特定电路进行混频,能够将高频率相位差测量转化为较低频率的相位差测量,扩大了被测信号的测量范围,增加了测量的精准度,使得应用范围更加广泛。

采用混频检相方法实现两路同频信号相位差的测量,为保证结果更具有一般性,设两路差频信号X1(t,f)和X2(t,f):

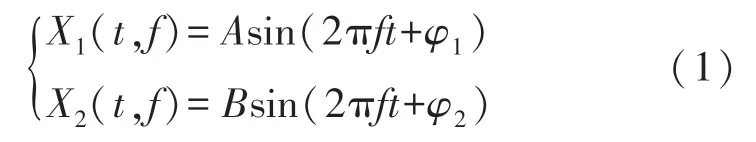
式中:A和B分别为两路被测信号的幅值,f为被测信号频率,φ1和φ2分别为被测信号初始相位。

设信号X0(t,f＋Δf):

式中:C为参与混频信号幅值,f＋Δf为参与混频信号频率。

将待比较的两路正弦信号分别与X0(t,f＋Δf)信号相乘:

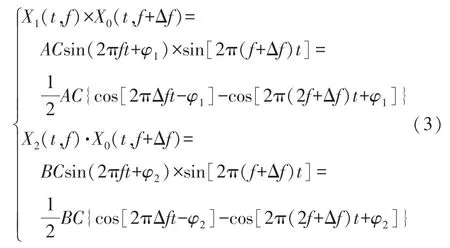
分析式(3)可知:两路信号与X0(t,f＋Δf)信号相乘,会得到幅值信号减半的差频信号与和频信号的叠加。由此可以对相乘后的两路信号进行低通滤波处理,保留差频信号:

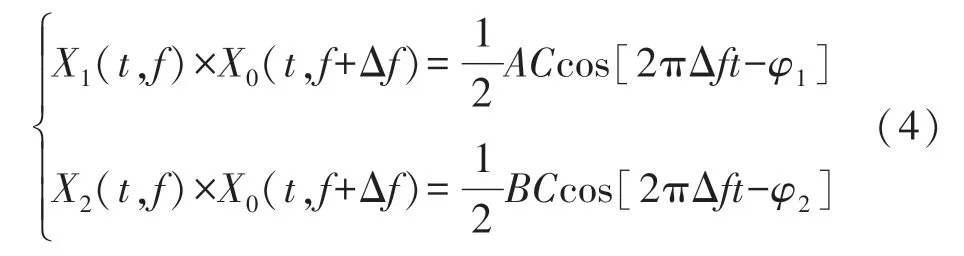
根据式(4)可知:滤波后的差频信号保留了相位差信息:

考虑到理论的一般性,将这个结论应用到方波信号中,因为方波中除了基波还存在许多高次谐波,所以对方波进行傅立叶分解。

对于周期T＝,幅值为1 的方波信号:

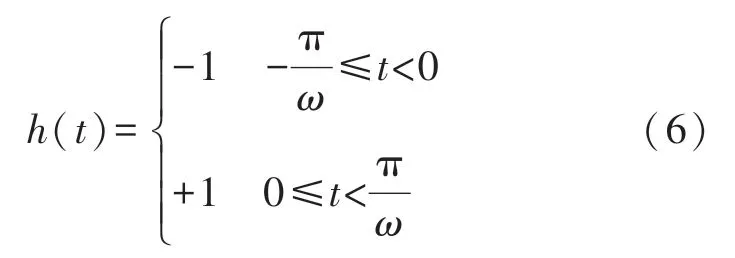
进行傅里叶分解:

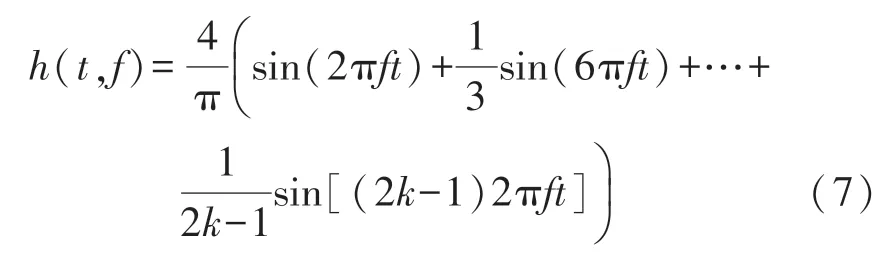
对方波信号傅里叶分解后相乘得到的情况进行分析,定义两个周期与相位不同信号h1(t,f)与h2(t,f):

对信号h1(t,f)与h2(t,f)相乘情况进行研究:

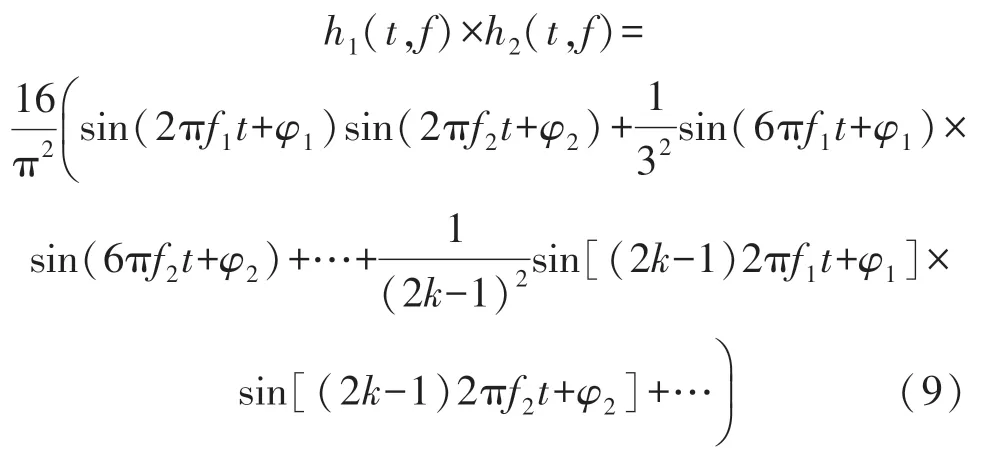
根据式(9)可知,两个信号相乘以后依然与正弦信号有着相似的特性:基波与谐波分别都有频率和的高频信号与频率差的低频信号。

对相乘的信号进行滤波,得到差频信号:

经过分析式(10)发现:该差频信号为保留被测相位差信息的三角波。

设两路方波信号B1(t,f)和B2(t,f):

设B0(t,f＋Δf)信号为:

基于上述分析,两路方波信号与B0(t,f＋Δf)信号相乘滤波后结果为:

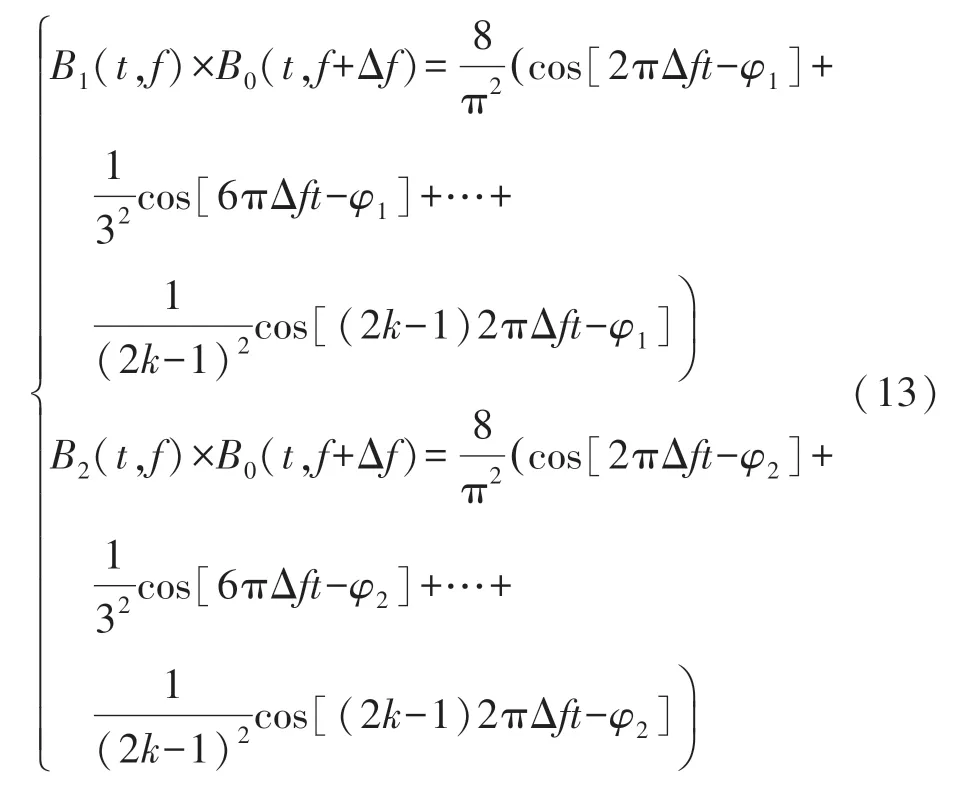
2 电路设计

系统硬件框图如图2 所示,当超声波传感器完成检测就会传出两路待测信号,混频电路可以在保留相位信息的同时进行频率的转换,方便测量；低通滤波电路可以过滤掉电路中的高频成分,保留包含相位差的低频信号；整形电路可以将波形进行转换；检相电路可以获取两路信号的相位差值,并输出相位信息。

图2 系统硬件框图

2.1 混频电路设计

混频电路如图3 所示。MC1496 芯片是根据双差分对原理设计的乘法器,具有极佳载波抑制比,实现频谱转换电路具有电路简单,调试方便的特点。应用芯片MC1496 极佳的特性设计混频电路,可以使得信号输出更加纯净,对混频信号产生的干扰小,输出增益可调。被测信号与参比信号通过混频电路,可以产生频率的偏移,将高频信号转变为低频信号,同时保留了相关的相位信息。

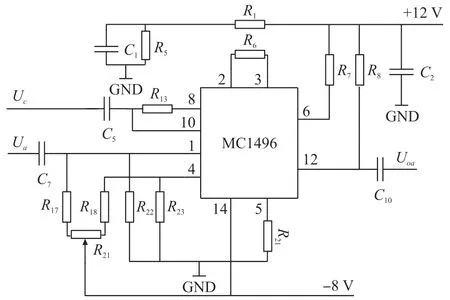
图3 混频电路

2.2 检相电路

检相电路如图4 所示,由两个D 触发器组成电路实现。D 触发器由上升沿信号触发,将两路经整形后的被测信号作为时钟端输入,两个触发器输入端始终置位高电平,D1 的输出端控制D2 的清零端,D2 的反向输出为D1 清零信号,D1 检测到上升沿信号输出高电平信号,D2 工作会将D1 清零,D1输出端信号的占空比体现了被测相位差信息。

图4 检相电路

D＝t/T,ϕ＝2πD,其中T为触发器输出信号的周期,t为高电平时间,D占空比,ϕ为被测信号的相位差。

3 仿真与试验

3.1 信号混频仿真实验

为了验证设计方案的准确性,在MATLAB 仿真软件中进行仿真验证,正弦信号实验参数如表1所示。

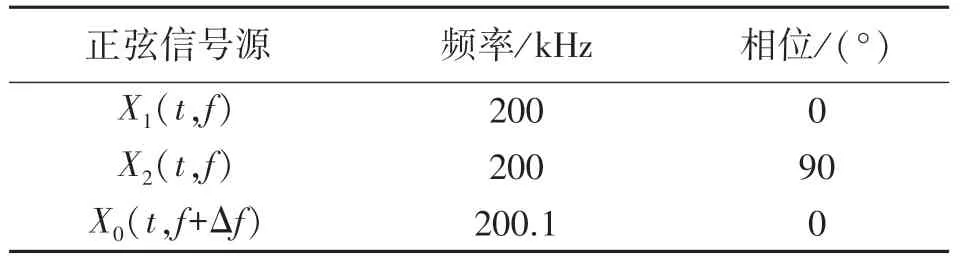
表1 正弦信号仿真实验参数

选取两路正弦信号源X1(t,f),X2(t,f),分别与给定信号X0(t,f＋Δf)利用乘法器进行混频操作,经过低通滤波电路(-3 db)后仿真波形如图5 所示,得到两路频率为100 Hz,相位差为90°,幅值减半的正弦信号。

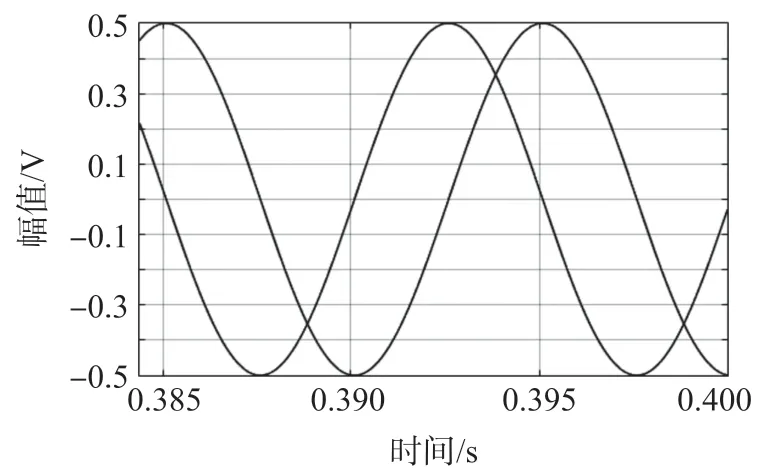
图5 正弦波实验波形图

方波实验参数如表2 所示。

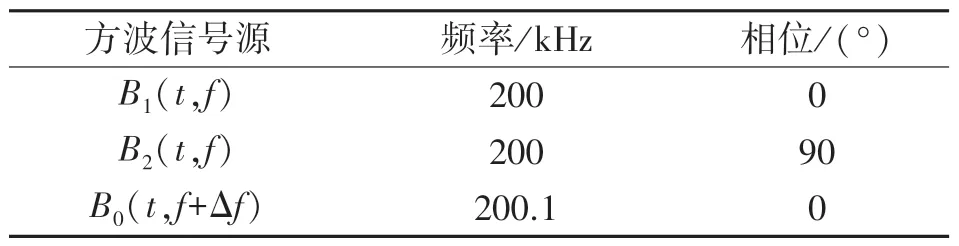
表2 方波信号实验参数

选取方波信号源B1(t,f),B2(t,f),分别与给定信号B0(t,f＋Δf)进行混频、滤波后仿真波形如图6所示,得到两路频率为100 Hz,相位差为90°,幅值减半的三角波信号。

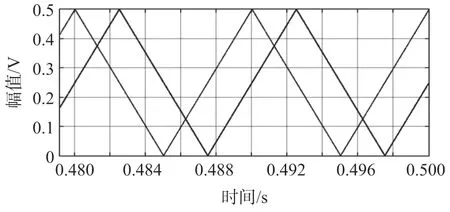
图6 方波实验波形图

3.2 检相实验及仿真结果

整形电路处理后的波形如图7 所示,得到两路频率为100 Hz,相位差为90°的方波信号,通过检相电路得到计算相位差所需信号,如图8 所示,该信号占空比D为0.25。

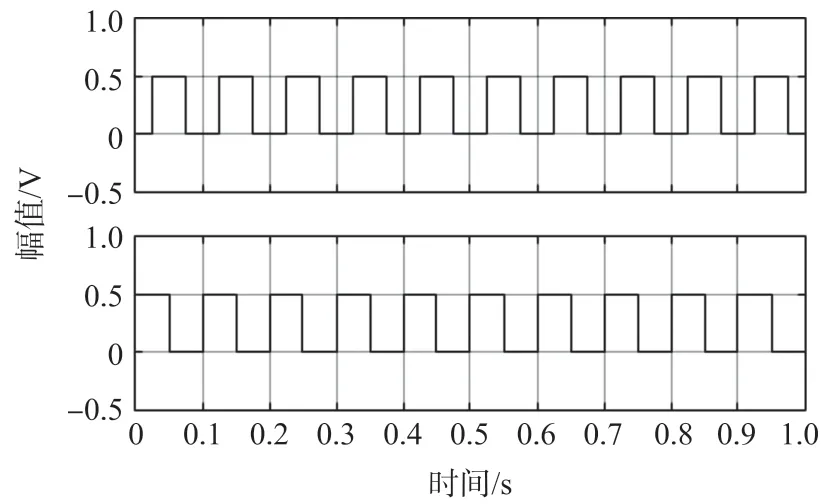
图7 差频信号波形图

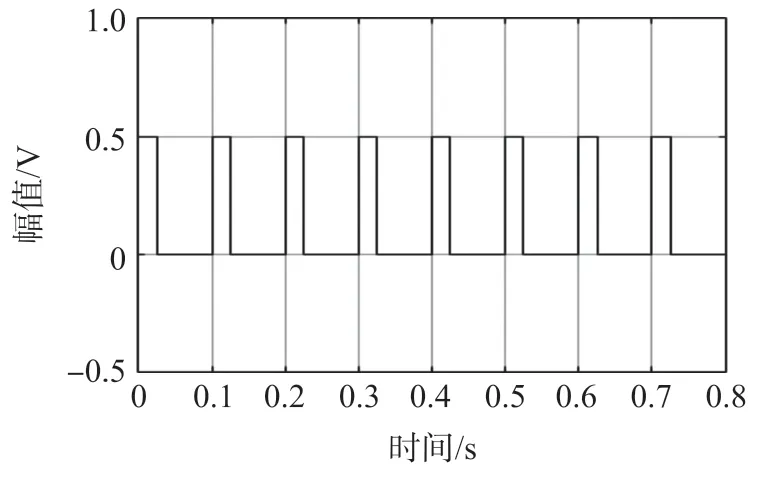
图8 仿真检相波形图

混频检相器实物如图9 所示,以单片机PIC16F883为微型控制单元,包括MC1496 混频电路、D 触发器检相电路等,可以实现对相位差的测量。取两路频率为200 kHz,相位相差为90°的正弦信号进行相位实验,如图10 所示。

图9 混频检相器实物

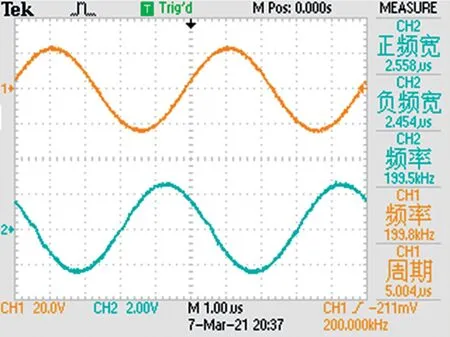
图10 被测信号波形图

经混频滤波后通过整形电路获得两路低频的保留相位差的方波信号,如图11 所示,最后由检相电路输出相位信息,如图12 所示,由此可以得出被测信号相位差为90°。

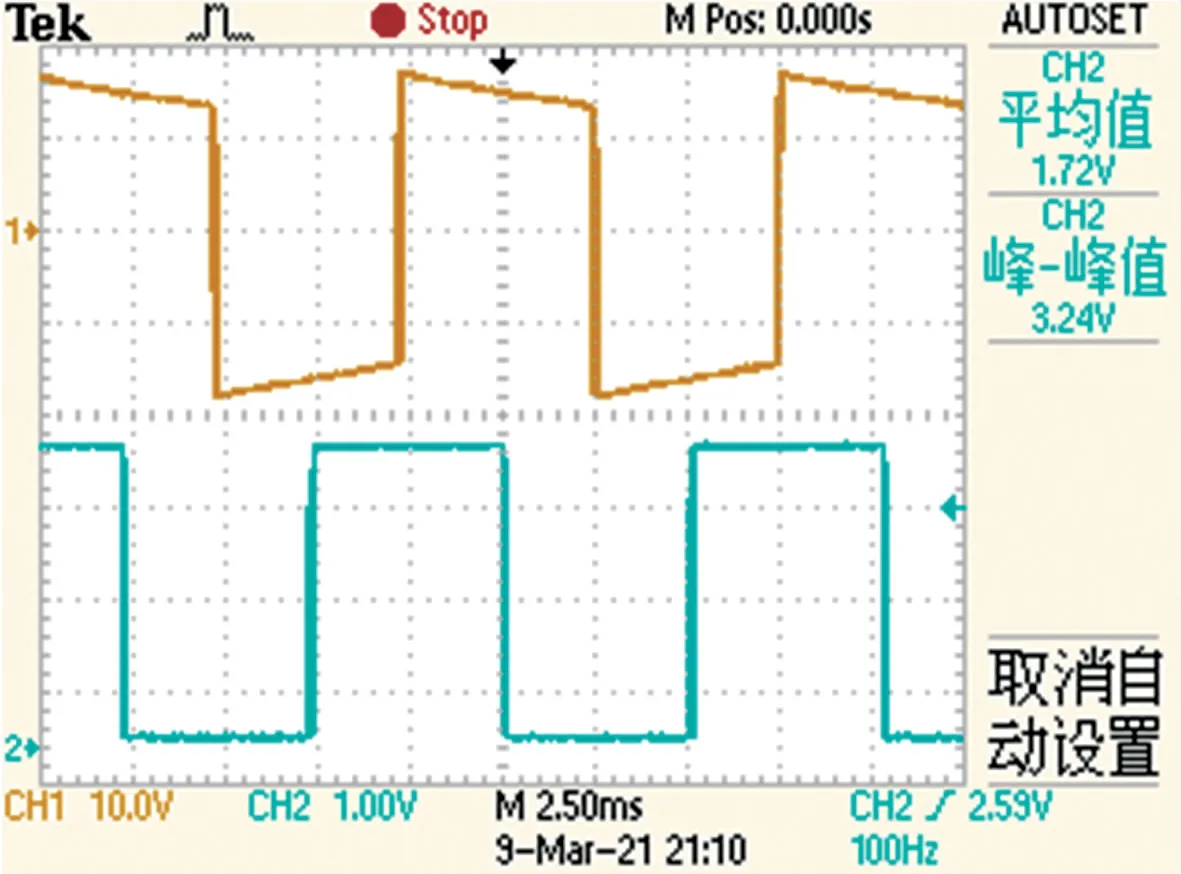
图11 差频信号实验波形图

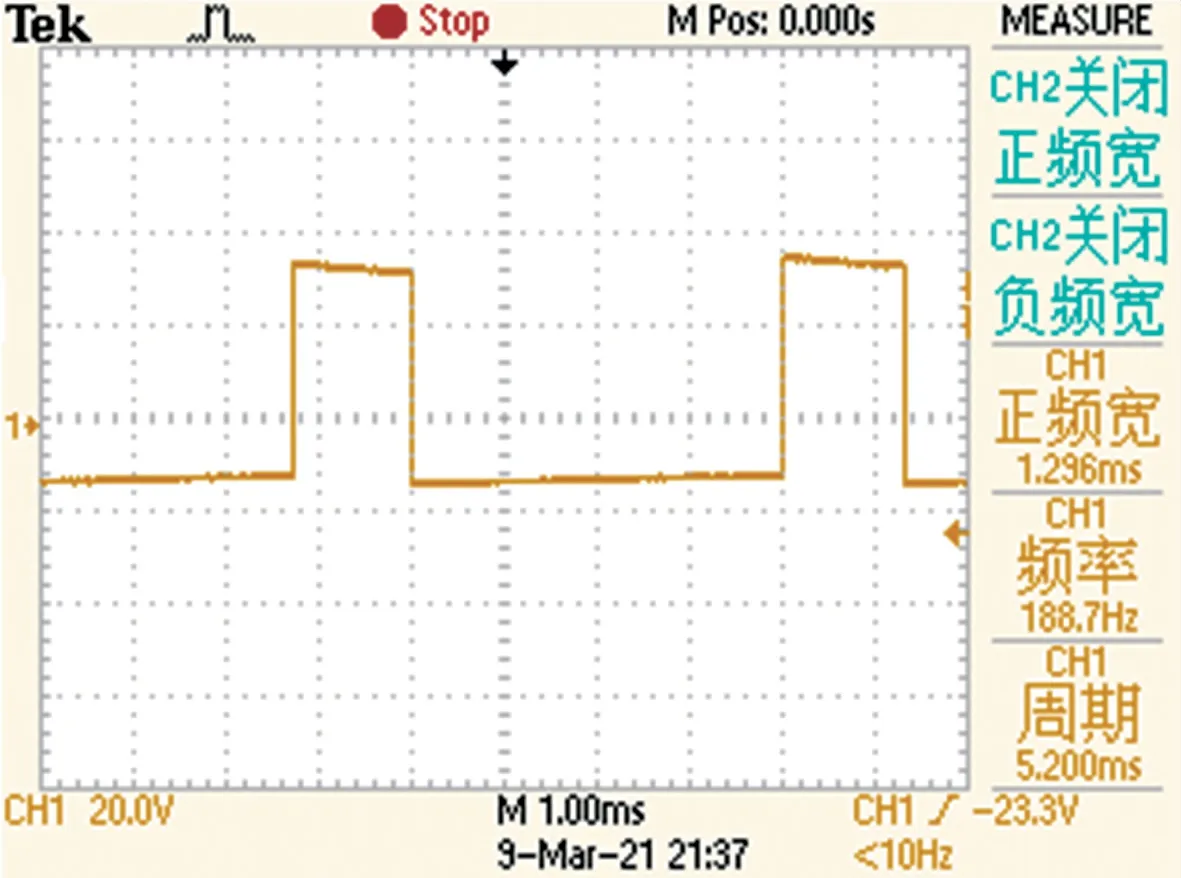
图12 实测90°占空比信号

调节待测信号的相位差值,使其分别为30°,60°和120°,通过示波器实测占空比波形如图13～图15 所示,对测试结果和实际值进行误差分析,分析结果如表3 所示。

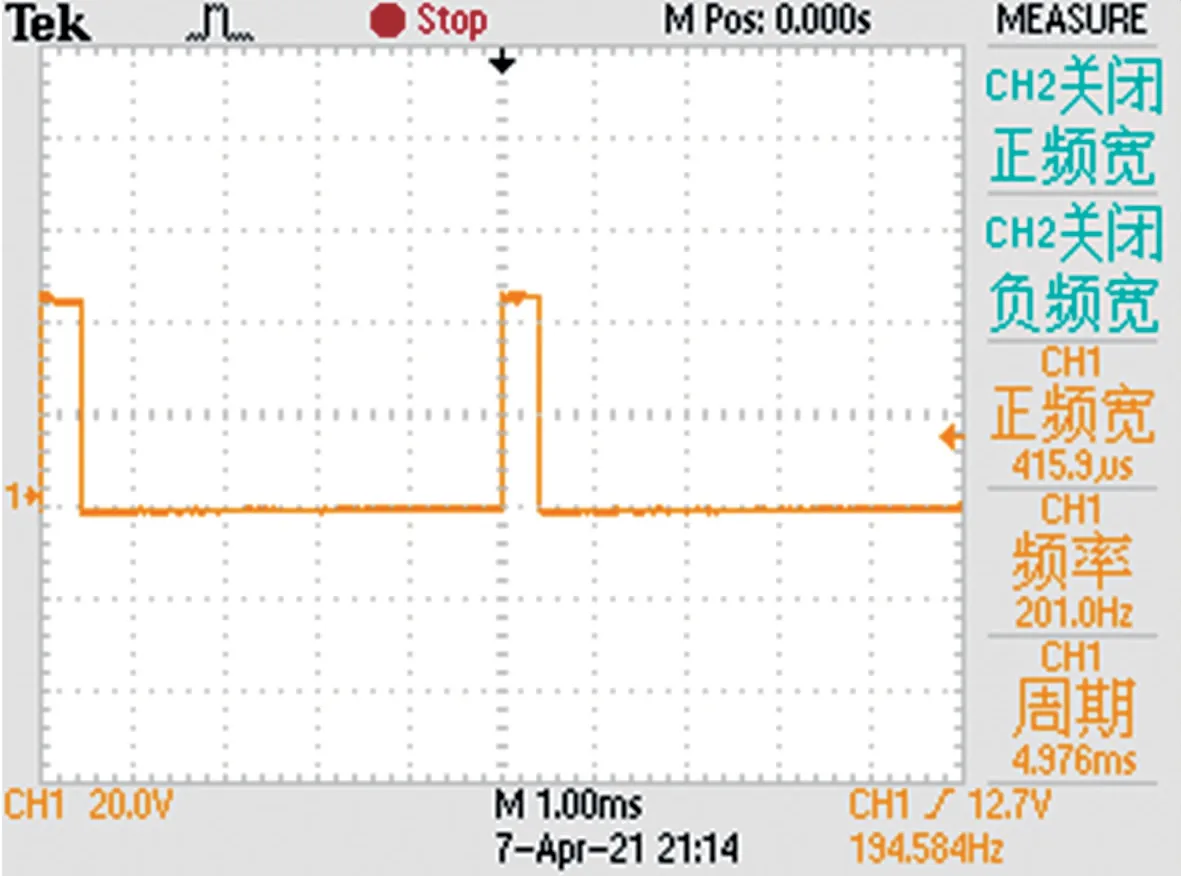
图13 实测30°占空比信号

图14 实测60°占空比信号

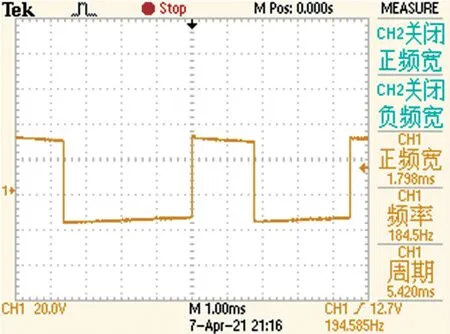
图15 实测120°占空比信号

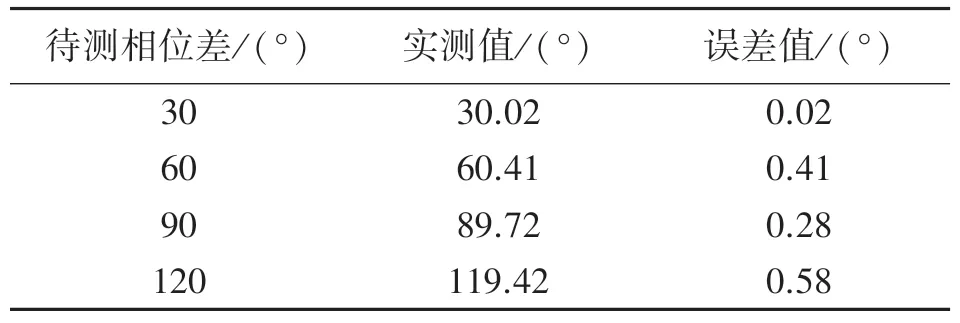
表3 实验测试结果

通过改变待测信号相位差值进行多组实验,结合表3 进行分析可得出结论:混频检相方法具有较小的测量误差,均在1°以内,验证了混频检相方法的正确性,表明该方法满足超声波相位差测量系统在工程上的应用需求。

4 结论

本文提出的应用于超声波测量的混频检相方法,能够准确地检测相位信息,扩大了被测信号的频率范围。通过频率为200 kHz,相位差为90°正弦、方波信号实验论证了混频方法,通过对相位差为30°,60°,90°和120°信号进行多组相位差实验证明了混频检相方法的可行性,实测误差均在1°以内,很好地满足了超声波测量过程中对测量精度的要求。