多孔径接收机中数字相干合成效率统计模型
向劲松,吕心浩
(重庆邮电大学 通信与信息工程学院, 重庆 400065)
0 引 言
在空间通信中,自由空间光(Free Space Optical, FSO)通信具有传输容量大、功耗低和保密性好等优点[1-2]。为了抑制大气湍流效应,在接收端可以采用自适应光学[3-4]和多孔径接收技术[5-6]。但自适应光学复杂且成本高,且该方案仅适用于整个望远镜接收,具有一定的局限性。多孔径相干光接收机使用多个小孔径望远镜接收信号光束,具有成本低、维护成本低和系统升级容易等特点。多孔径相干光接收机通过光束相干合成[7-8]或数字相干合成将多路信号合为一路。光束相干合成模拟元件的高光学复杂度和高插入损耗,很难扩展到大量信号。数字相干合成使用多个检测器将每个支路的光信号转换为电信号,然后将多个电信号进行数字相干合成[9-13]。
最大比合并和等增益合并(Equal Gain Combining, EGC)是常用的合成算法。由于EGC可以提供接近最大比合并的性能,并且具有实现复杂度较低的优点[14],在多孔径相干光接收机中被广泛使用。假设有理想的时延补偿,文献[11]给出了一种基于EGC数字信号处理的逐步相位对齐算法,实现了4路激光通信信号的无损相干合成;基于文献[11],Rao和Tu研究了计算复杂度与平均合成效率(Combining Efficiency, CE)之间的关系[15-16]。然而,载波恢复和误码率与相干合成后的合成信噪比(Signal-to-Noise Ratio, SNR)具有非线性关系[5,17]。因此,仅通过平均CE来评估多孔径相干光接收机的性能是不准确的。为了体现CE的随机性,应该给出CE的概率密度函数(Probability Den-sity Function, PDF)。
本文建立了基于EGC的CE统计模型,并推导出PDF的准确表达式。在考虑孔径选择的情况下,比较了不同合成孔径数量下基于EGC的CE。并基于该模型,提出了一种基于最大CE期望的孔径选择方案。
1 CE统计模型
图1所示为多孔径数字相干合路接收机原理图,激光束通过大气信道后,由多根接收天线独立输入到相干接收机中。并行的空间光信号共享同一个窄线宽本振激光器。在前端补偿模块中,对每组数字化的I和Q信号进行补偿,以平衡I和Q信号电平以及远程I和Q信号时序偏差。在时钟恢复模块中,时钟恢复算法确保每个信号以符号周期为模对齐,以便知道每个符号的中心位置。接下来,使用时延估计算法去除不同孔径接收到的信号之间的相对延迟。然后,各支路的相对相位由相位对齐模块对齐并相干合成。数字相干合成后,在载波恢复模块中应用载波恢复算法,估计合成信号的频偏和相偏,恢复传输的符号。
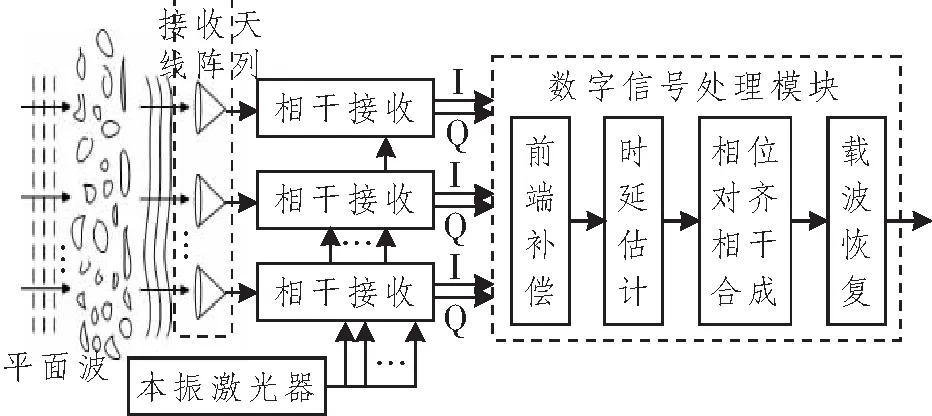
图1 多孔径数字相干合路接收机原理图Figure 1 Schematic diagram of multi-aperture digital coherent synthesis receiver
图2所示为相位对齐和相干合成算法框图。相位对齐的核心思想是以某一信号为参考,调整其他信号的相位与参考信号的相位一致,实现相位对齐。第一次合成以信号S1为基准,估计和补偿信号S1和S2之间的相位差。信号S1和S2合成后,将两个信号的和作为参考信号,并与信号S3合成。重复该过程直到所有信号都被合成。

图2 相位对齐和相干合成算法框图[11]Figure 2 Block diagram of phase alignment and coherent synthesis algorithm
理想时延对齐后,按SNR由高到低排列,第n个相移键控(Phase Shift Keying,PSK)调制信号的第k个码元Sn(k)为
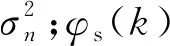
第n路PSK调制信号的SNR可表示为
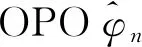
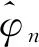
我们可以从估计两个光信号(S1和S2)之间的OPO开始。将式(1)代入式(3)可得:
式中,nC为Csum的噪声项,即

式(5)可重写为
式中,Δφ1为加性观测相位噪声(Additive Observation Phase Noise, AOPN)[20]。在高SNR条件下,Δφ1可被近似为高斯随机变量,均值为0,方差为
通常,OPO估计误差Δφ1的值远小于1,因此式(10)可近似为
因此,两个光信号的合成效率CE2可通过下式得到:
式(12)表明,CE2是具有一个自由度的卡方随机变量的线性函数,其均值E(CE2)、方差D(CE2)和PDFfCE2(x)分别为
式中,Γ(·)为伽马函数。综上所述,基于式(9)和式(13~15),我们得到了两路光信号合成的CE统计模型。由式(13~15)可知,CE是与各个支路SNR和符号数量M相关的随机变量。

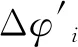
式中:XN=[Δφ1Δφ2… ΔφN-1]T;DN为XN的系数矩阵。
基于式(18),N路信号的CE可表示为
式中,XN服从多元高斯分布,即XN~NN-1(0,ΣN),ΣN为(N-1)行(N-1)列的对角矩阵。通过使用文献[20]给出的AOPN模型,ΣN中第p行q列的元素ΣN(p,q)可由下式给出:
需要注意的是,在得到特征值cN,1,…,cN,N-1之前,需要计算DN和ΣN,其中DN可直接由幅度A1,…,AN得到。然而,根据式(20)和(21),ΣN只能由ΣN-1间接获得。换句话说,ΣN需要由Σ2开始递归计算得到,其中Σ2为式(9)给出的Δφ1方差。
因此,基于式(19),N个支路的CE可近似为自由度νN的卡方随机变量YN的线性函数,即
均值E(CEN)、方差D(CEN)和PDFfCEN(x)分别为
式中,
由式(24~27)可知,CE主要受每次合成的符号数量M和各支路SNR的影响。
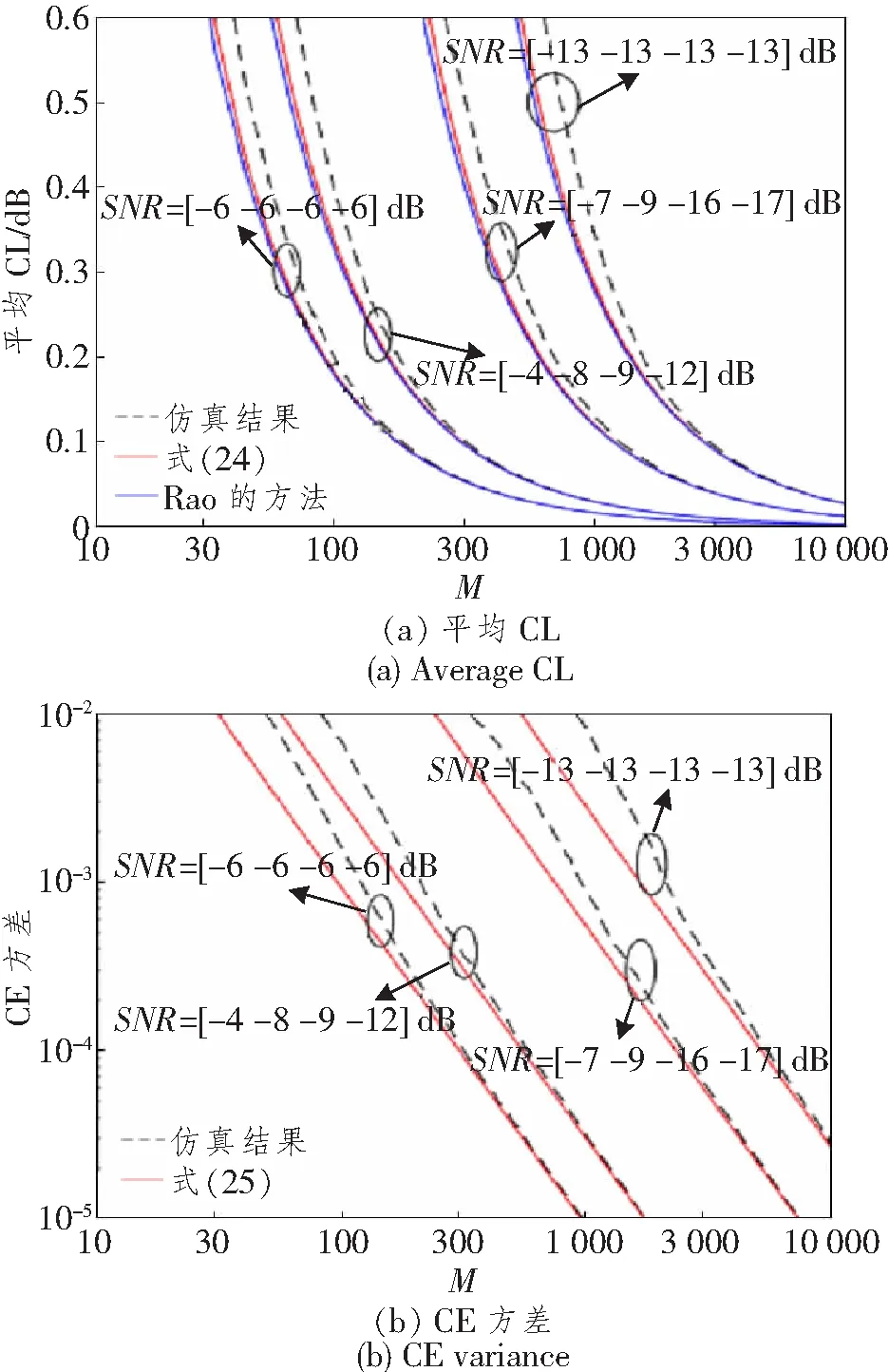
为了降低系统复杂度或提高合成SNR,我们可选择多个SNR较高的支路进行合成,而不将所有支路全部合成。孔径选择系统的SNR增益CEN,n可以定义为n(2≤n 式中, 均值E(CEN,n)、方差D(CEN,n)和PDFfCEN,n(y)分别为 在本节中,我们将给出数字相干合成与EGC的数值结果。在以下结果分析中,CL用于评估平均CE,CE用于评估CE的方差和PDF。在不同孔径数和SNR方案的情况下,对仿真结果和分析结果进行比较。每个仿真数据点的蒙特卡罗模拟运行次数设置为106。光信号为10 Gbit/s非归零二进制相移键控(Binary Phase Shift Keying, BPSK)信号。每个支路的OPO从-π到π中随机选择。激光频率偏移和激光线宽分别等于500 MHz和10 kHz。 图3所示为在不同SNR下合成4个信号的平均CL和CE方差。图中,横坐标表示第1个信号的SNR,记作SNR1;仿真结果表示数据由蒙特卡洛模拟得到;式(24)和(25)分别表示数据由式(24)和(25)计算得到;SNR方案1表示4个支路的SNR相同,SNR方案2表示两个相邻支路的SNR差值为1 dB,即SNRi(dB)=SNRi-1(dB)-1 dB;SNR方案3表示两个相邻支路的SNR差值为2 dB。如图3(a)所示,与Rao[16]的方法相比,仅在低SNR下,本文所提方法的性能略有改善。随着SNR的不断增加,预测平均CL与实际平均CL之间的误差逐渐减小。如图3(b)所示,当平均CL较低时,式(25)预测的CE方差与实际CE方差相匹配。随着SNR的不断减小,预测CE方差与实际CE方差之间的误差逐渐增大。 图3 M=70和N=4时不同SNR组合方案下的平均CL和CE方差Figure 3 Average CL and CE Variances under different SNR combination schemes when M=70 and N=4 图4所示为不同符号数量M和SNR组合方案下的平均CL和CE方差。如图4(a)所示,平均CL随着M的增加而减小。此外,对于相同的平均CL,所需的M值随着SNR的降低而增加。例如,当平均CL为0.1 dB时,与SNR=[-6 -6 -6 -6] dB的情况相比,SNR=[-13-13-13-13] dB的情况下,M值增加约20倍。此外,实际CL和规定CL之间的差异随着M的增加而减小。如图4(b)所示,CE方差随着M的增加而减小,并且所需M值随SNR的降低而增加。随着M的增加,预测的CE方差与实际CE方差之间的误差逐渐减小。 图4 N=4时不同M和SNR组合方案下的平均CL和CE方差Figure 4 Average CL and CE Variances under different M and SNR combinations when N=4 图5所示为N=4时不同SNR组合方案下CE的PDF。如图5(a)和5(b)所示,由于每个支路的SNR相差不大,2、3和4孔径的CE随着所选孔径数量的增加而增加。如图5(a)和5(b)所示,平均CL和CE方差随着M的增加而减小。因此,与图5(a)相比,当所选孔径数相同时,图5(b)中CE的PDF曲线向右移动并变窄。图5(c)和5(d)给出了不同选择孔径和M下CE的PDF曲线。由图可知,与全合成方案相比,3个孔径的合成方案使CE取较大值的概率更高。图5(c)和5(d)中,2、3和4个孔径的实际平均CL分别为[1.40 0.04 0.55] dB和[1.26 -0.11 0.26] dB。由平均CL也可看出,3孔径合成方案优于全孔径合成方案。这是因为,第4支路的SNR太小,无法为EGC提供正的SNR增益。注意到在某些情况下,3孔径的CE大于1,说明3孔径的实际合成SNR大于全孔径合成的理想合成SNR。此外,随着M的增加,合成性能都有所提高,并且理论分布与实际分布曲线非常吻合。 图5 N=4时不同SNR组合方案下CE的PDFFigure 5 CE probability density function under different SNR combinations with N=4 图6所示为16路信号在不同SNR合成下的平均CL和相应CE方差。与N=4的情况类似,横坐标表示第1路信号的SNR,SNR方案1表示16个支路的SNR相同;SNR方案2表示两个相邻支路的SNR差值为0.5 dB; SNR方案3表示两个相邻支路的SNR差值为1 dB。如图6(a)所示,随着SNR不断增加,平均CL以及预测平均CL和实际平均CL之间的误差将逐渐减小。与N=4的情况相比,相同平均CL下每个支路所需的SNR由于M的增加而降低。如图6(b)所示,随着SNR的不断增加,预测CE方差与实际CE方差之间的误差逐渐减小。 图6 M=200和N=16时不同SNR组合方案下的平均CL和CE方差Figure 6 Average CL and CE Variances under different SNR combinations at M=200 and N=16 图7所示为N=16时不同SNR组合方案下CE的PDF曲线。如图7(a)和7(c)所示,全合成的平均CL为0.5 dB;如图7(b)和7(d)所示,全合成的平均CL为0.2 dB。如图7(a)和7(b)所示,当每个分支的SNR相同时,随着选择孔径的数量增加,合成性能变得更好。全合成方案优于孔径选择方案。与图7(a)相比,图7(b)中的全合成和孔径选择的性能差异更为显著。如图7(c)和7(d)所示,PDF的峰值随着所选孔径数n的减小而向右移动。这表明,随着所选孔径数量的增加,合成性能变得更差。这是因为,相邻分支之间的SNR差值增加到1 dB,使得EGC提供负SNR增益。 图7 N=16时不同SNR组合方案下CE的PDFFigure 7 CE probability density function under different SNR combinations at N=16 EGC算法直接把全部信号合并相加。不同于EGC算法,孔径选择系统选取适当的合成孔径数,在降低系统计算复杂度的同时提高了系统性能[23]。基于CE的统计模型,本文提出了最优孔径选择方案,在将接收信号按SNR强度递减顺序排列后,由式(30)依次计算CE期望,自适应输出包含最大CE期望的孔径组合,所选孔径数量nopt为 该方法只需计算每种孔径组合的CE期望,计算复杂度低。 图8 孔径选择接收机误码率曲线Figure 8 BER curve of aperture selection receiver 基于AOPN模型,本文推导出了用于多孔径FSO接收机数字相位对齐的CE统计模型。 其可通过Satterthwaite方法近似表示为卡方分布的线性函数。仿真结果表明,在大多数情况下,该模型在不同孔径数量和SNR条件下是有效的。通过模型比较了EGC的孔径选择和全合并方案。随着各支路SNR差距的增大,孔径选择的性能会逐渐提高。这项工作可以为数字相干合并后的误码率性能评估提供有价值的指导。2 系统仿真及结果分析




3 统计模型在孔径选择系统中的应用
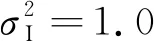

4 结束语

