大规模检测算法在光通信系统中的研究

樊峰菊，张建勇，宋义梅，胡伟国，密术超

(北京交通大学 a.光波技术研究所； b.EMC全光网络与高级电信网络重点实验室，北京 100044)

0 引 言

模分复用(Mode Division Multiplexing, MDM)被认为是增加光通信系统容量的一种潜在方式，其利用多模光纤(Multi-Mode Fiber, MMF)或耦合芯的空间自由度多芯光纤(Multi-Core Fiber, MCF)以传播模式传输数据[1]。目前，已经提出了各种类型的具有100多种空间模式的MDM光纤，并对其传输的可行性进行了研究[2-6]。 然而，模式相关损耗(Mode Dependent Loss, MDL)限制了光纤链路系统的基本容量，成为目前需要面对和克服的巨大挑战[7]。

几种多输入多输出(Multiple Input Multiple Output,MIMO)检测算法，如非线性最大似然(Maximum Likelihood,ML)检测、迫零(Zero-Forcing,ZF)检测和最小均方误差(Minimum Mean Square Error,MMSE)均衡等已经被引入来研究少模光纤(Few Mode Fiber, FMF)中对MDL的补偿性能[8-12]。随着模式数量的增加，对于具有成百上千个传播模式的MDM系统，这些算法将表现出很高的计算复杂度。在无线通信系统中，大规模MIMO是传统小规模MIMO系统的放大版本，其实际上使用数百或理论上数千个天线元件[13-14]。相应地，已经提出了几种类型的大规模MIMO检测算法，包括矩阵求逆[15]、近似矩阵求逆[16-18]和盒约束检测[19-22]等。然而，这些先进的大规模MIMO检测算法目前仅应用于无线系统[23-25]，尚未在MDL受损的MDM光纤传输中应用。

本文将把3类大规模MIMO检测算法应用到MMF传输系统中。第1类是MMSE，其在所有矩阵求逆算法中具有较低的计算复杂度和较好的性能；第2类是近似矩阵求逆检测，分别是高斯-塞德尔 (Gauss Seidel, GS) 法和共轭梯度 (Conjugate Gradient, CG) 法；最后一类是盒约束检测，包括优化的基于坐标下降的盒约束(Optimized Coordinate Descent based BOX constraint, OCDBOX)，基于无穷范数的乘子交替方向 (Alternating Direction Method of multipliers based Infinity-Norm, ADMIN) 法。上述检测算法的性能和计算复杂度将在MDL受损的MDM光通信系统中进行研究。

1 MDM系统

本文仿真基于一种端到端的MDM传输链路，如图1所示，MDM系统可以建模为K个独立光纤段的级联，每个短段建模为随机矩阵。假设其支持D个正交传播模式(包括空间和偏振自由度)，整个传输矩阵建模为[26-27]

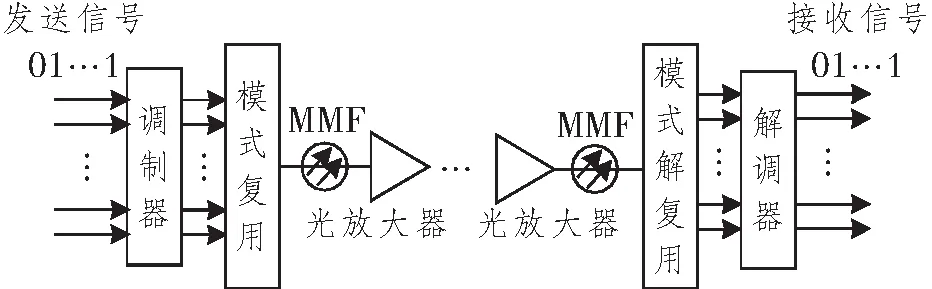
图1 基于MMF的MDM系统Figure 1 MDM system structure based on MMF

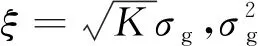
2 检测算法

将3类大规模MIMO检测算法应用到MDM光纤传输系统中：第1类是MMSE，其在所有的矩阵求逆算法中具有较低的计算复杂度和较好的性能；第2类方法是近似矩阵求逆检测，包括GS和CG；最后是盒约束检测，包括OCDBOX和ADMIN。在MDL存在的情况下，将研究上述检测算法的性能和计算复杂度。

2.1 MMSE

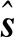
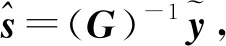
2.2 CG

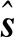
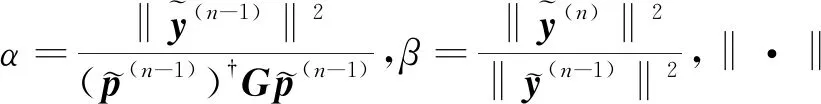
2.3 GS

GS方法也可用于求解D维线性方程Ax=b，在文献[18]中描述，GS方法要求A为厄米正定矩阵，MMSE检测算法中的G正好满足这一要求，此时G可以分解为

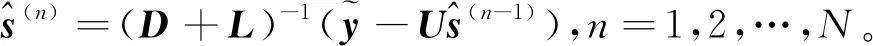
2.4 OCDBOX

BOX 约束均衡是ML检测算法的凸松弛，其将约束s∈D(为星座内的符号集合)松弛到星座集周围的凸多面体上。 这使我们能够通过有效的凸优化恢复信号。 OCDBOX是一种BOX均衡算法，其通过一系列简单的坐标更新得到大量凸优化近似解, 是求解高维线性系统逆问题的一种迭代算法。第u个模式的估计解为[21]

式中：hu为传递矩阵H的第u列；={sR+jsI∶sR,sI∈[-α,+α]}是围绕星座集合的凸多面体,sR为符号s的实部，sI为符号s的虚部，α为包围盒方形星座的最紧半径，j为复数中的虚部。

2.5 ADMIN

ADMIN是另一种BOX均衡算法，其通过交替最小化来优化无约束优化的部分，并将一个大的全局优化问题分解成多个更小的、更容易解决的局部子问题，其表达式如下：

g(z)为凸集上的指示函数：

式(6)所对应的增广拉格朗日方程为

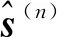
3 系统性能

本文仿真了一种32模式的32×32 MDL受损的MDM光通信传输系统，整个过程考虑了模式耦合以及MDL的影响，其中模式耦合通过随机酉矩阵来表示, 而整个累积MDL服从高斯分布[27]，文中选取MDL方差分别为ξ=5和10 dB时进行仿真。文献[29]基于MDL光纤系统，推导了链路平均MDL与传输距离之间的理论表达式并进行了验证，从文献[29]中可知ξ=5和10 dB对应的光纤链路传播距离大约分别为400和1 560 km。假设每个短段所传输的距离为13 km[30], 则ξ=5和10 dB所对应的短段K大约分别为30和120。系统分别使用正交相移键控 (Quadrature Phase Shift Keying,QPSK) 和 16 级正交幅度调制(16 Quadrature Amplitude Modulation, 16QAM)进行符号传输，并在接收端分别使用以上5种检测算法进行检测。基于以上传输系统，文中分析了5种检测算法的收敛与误码率(Bit Error Rate，BER)性能。

3.1 收敛性能

图 2(a) 所示为QPSK调制方式下不同检测算法的收敛性能。ξ=5 dB时SNR=14 dB；ξ=10 dB时，SNR=25 dB。由图可知，当ξ=5 dB时，ADMIN的收敛速度略快于其他算法；当ξ=10 dB时，其收敛速度比其他算法快得多。此外，当ξ增加时，OCDBOX、CG和GS需要更多的迭代才能收敛。图2(b)所示为16QAM方式下不同检测算法的收敛性能。由图可知，ξ=5 dB时，ADMIN的收敛速度稍慢于其他算法；ξ=10 dB时，ADMIN在所有4种迭代算法中收敛最快。此外，ξ=10 dB与ξ=5 dB的情况相比，4种算法需要更多的迭代才能收敛。根据图中的结果，选择每种算法所需的迭代次数，如表1所示。

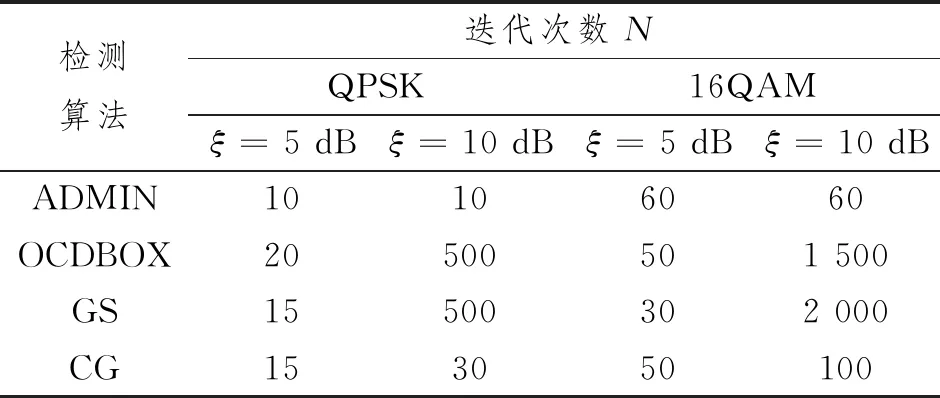
表1 各种检测算法所需的迭代次数

图2 ADMIN、OCDBOX、GS和CG在MDM系统中的收敛性能Figure 2 Convergence performance of ADMIN,OCDBOX, GS and CG in MDM system

3.2 BER性能

第3节给出5种算法的BER性能如图3所示。图3(a)调制格式为QPSK。结果表明，ξ=5 dB时, ADMIN、CG和MMSE具有相似的性能，OCDBOX在所有算法中性能最好，并且在BER=10-5时，OCDBOX的性能优于ADMIN、 CG和GS约3 dB。此外，GS检测算法性能最差，并且在SNR=22 dB之后，BER性能稳定在10-5附近。ξ=10 dB时，在BER=10-5，OCDBOX的性能比 ADMIN(MMSE)大约要好5 dB(9 dB) ，GS性能最差，并且在高SNR时，GS性能会有所下降。图3(b)所示为16QAM的BER性能。ξ=5和10 dB时，显示图中OCDBOX仍然是性能最好的，ADMIN性能次之。

图3 32×32模式下MDM系统中不同MDL值时的BER性能比较Figure 3 Comparison of BER performance in MDM systemwith different MDL values in 32×32 mode

4 计算复杂度

本文中计算复杂度定义为估计信道输入信号所需的复数乘法次数[11]。MMSE检测涉及矩阵求逆，计算公式为D3+3D2[11]。CG和GS的复杂度分别为N(D2+6D)和(N+1)D2+4D[17-18]。OCDBOX和ADMIN需要的复杂度分别为N(8D2+4D)和N(2D2+D)[21-22]。

表2 所示为MDM系统中不同检测算法的计算复杂度。对于QPSK调制，虽然OCDBOX实现了最佳性能，但当ξ=5 dB时，其复杂度约为ADMIN的8倍；当ξ=10 dB时，其复杂度约为ADMIN的200倍。对于16QAM，OCDBOX的计算复杂度最高，而MMSE的计算复杂度最低。随着模式数量的增加，ADMIN收敛所需的迭代次数会远低于模式数量，因此ADMIN对于16QAM的复杂度将低于MMSE。

表2 32×32模式下MDL光通信系统中各算法的计算复杂度比较

5 结束语

本文研究了5种大规模检测算法，并且在MDL受损的MDM光纤信道中比较了其性能和复杂度。OCDBOX检测算法具有最好的性能，但是有更高的计算复杂度。QPSK和ADMIN检测算法以较低的计算复杂度优于MMSE，但是其性能低于OCDBOX。16QAM和ADMIN检测算法计算复杂度高于MMSE，但是其性能明显优于MMSE。GS和CG的性能较差，并且在高SNR时，GS性能会有所下降。整体来看，在MDL受损的MDM光纤通信系统中，ADMIN检测算法在性能和复杂度方面具有明显优势。这为今后进一步的研究奠定了基础。在不增加ADMIN复杂度的前提下提高其性能是接下来研究的重点。