光子探测激光测距的目标跟踪建模与仿真
蒋 燕,孙志峰,周智睿,孙 通,饶 强,殷天峰
(国网湖北省电力有限公司信息通信公司, 武汉 430000)
0 引 言
由于空中各种噪声的影响,传统的激光雷达不能直接根据极其微弱的回波信号来测量目标的相对位置,因此在接收端需要有一个灵敏的探测器来接收微弱的回波信号。近年来,单光子计数方法利用弱光照射下光子探测器输出电信号自然离散的特点,采用脉冲甄别技术和数字计数技术识别并提取出极其微弱的信号[1-2]。单光子探测技术信噪比高、抗漂移性好、时间稳定性好,便于计算机模拟仿真。但是到目前为止,关于单光子计数技术的文献大多集中于单光子计数硬件系统的设计[3-4],对于数据处理部分也仅局限于测量静态目标的相对距离[5-8],目前还未查到关于光子探测激光测距跟踪运动目标的相关文献。
本文以单光子技术测量运动目标的相对距离为背景,利用实验得出的光子探测器的回波强度和噪声强度经验公式,对光子探测器接收的回波数据进行仿真并采用图像处理的方法,从大量的回波数据中提取出目标的运动轨迹。
1 回波模型
某一飞行器正以一定的速度接近一个以恒定速度运动的目标。飞行器上装有激光器来发射脉冲,同时有光子探测器来接收光子回波。在运动过程中,飞行器的运动状态在一维空间中可以随时改变(即可以加速、减速和匀速)。通过发射机接收到的光子,根据脉冲雷达测距公式可以生成时空二维回波事件的散点图。
1.1 飞行器与目标之间的相对距离
本文通过分析目标相对飞行器的运动状态建模和仿真,涉及到运动状态(距离、速度和加速度)均为目标相对飞行器的运动状态。假设Ri(i=1,2,3,…)为一个周期开始的初始距离;t1为发出的脉冲与目标相遇所用的时间;t2为脉冲遇到目标产生回波信号返回过程中被飞行器接收所用的时间;v0为初始速度;R为飞行器收到信号回波时与目标的相对距离;c为光速。
对于匀速运动,接收回波光子的时间计算表达式如下:
对于匀加速运动,a为加速度,接收回波光子的时间计算表达式如下:
计算完延迟时间后,根据测距公式即可计算出理想运动状态下飞行器根据接收的信号回波测量出与目标之间的距离。
1.2 接收信号的回波光子强度与回波噪声强度
激光测距时,影响系统性能的主要因素有:激光单脉冲的能量Et、目标反射率ρ、接收系统光学效率ηr、激光发射系统光学效率ηt、大气透过率τ、光学系统口径D、激光发散角α和探测器灵敏度等。激光测距对远距离的点目标测距时,探测器上接收到的能量[9]表达式如下:
式中:Er为探测器接收到的功率;Ar为有效接收面积;At为目标雷达的截面积;θi为太阳入射方向与目标法向夹角。
当目标处于日照区时,目标表面的反射光会降低探测器的性能,此外,探测器本身的暗计数也会在一定程度上引入噪声。上述噪声信号会产生较高的虚警数据,给后续的距离数据提取带来很大的压力。因此,在系统设计中需要最大限度地降低背景噪声对探测器的影响。假定视场角为θfov,太阳光谱照度为E,ηq为光子探测器的量子效率,滤光片带宽为Δλ,H为普朗克常量,测距系统接收到的背景光噪声功率P的表达式如下:
探测器上每秒接收到的平均光子事件次数为
式中:hν为532 nm单光子能量;ndark为探测器本身的暗计数;tgate为门控信号宽度;在激光采样次数fpulse一定的情况下,噪声事件的次数主要与滤波片带宽、探测器象元视场角、望远镜口径、探测器暗计数以及门控信号宽度有关。
1.3 回波概率
根据统计光学理论,激光测距中目标表面散射回来的激光回波信号在强度分布上是一个泊松分布[2]。因此,此处可以采用泊松分布来近似系统地探测模型中接收回波的个数。根据光子计数激光测距的原理,将探测的距离分成若干个距离栅格(每个距离栅格作为系统的观测精度,在该精度内最多只能接收一个光子回波信号),每个距离栅格对应激光探测过程中的一个时间段,该时间段内探测器能探测到光子回波信号的概率为
式中:Nsn(i)=Nn(i)+Ns(i),Nsn(i)为第i个距离单元内回波光子信号与回波噪声的总个数,Ns(i)为第i个距离单元内回波光子信号的平均个数,Nn(i)为第i个距离单元内回波噪声的平均个数;Psn(i)为第i个距离单元内光子回波出现的概率。
1.4 生产回波事件
高噪声、低信号强度是光子探测回波数据的特点。在回波事件中包含回波光子信号和回波噪声。根据统计光学可知,在基于光子计数的激光测距中,探测器接收到的光子数目满足负二项式分布[2],由于负二项式分布的曲线是由一个个小阶梯构成,因此在有限的时间段内,可以将探测器接收到的回波信号看作是均匀分布。
在一段时间间隔内,回波光子落在未知斜率的一段直线上(假定飞行器进行匀速运动),背景噪声在距离门内是随机分布的,可以假定背景噪声遵循均匀分布特征。根据式(6)分别计算出每个周期内回波光子和噪声出现的总概率,然后按照每个周期的概率生成均匀分布的随机数,满足随机数小于等于理论概率的事件记作1,不满足的记作0。然后在每个周期内提取Psn=1处的回波作为接收器接收到的事件。每个周期内的Psn=1的事件都对应有出现回波,根据每个周期内回波出现的时间点,可以计算每个周期内接收到回波事件所对应的目标与飞行器间的距离,这些回波事件是一些杂乱的散点(即为Psn=1的回波事件),如图1所示,信号被淹没在噪声中。
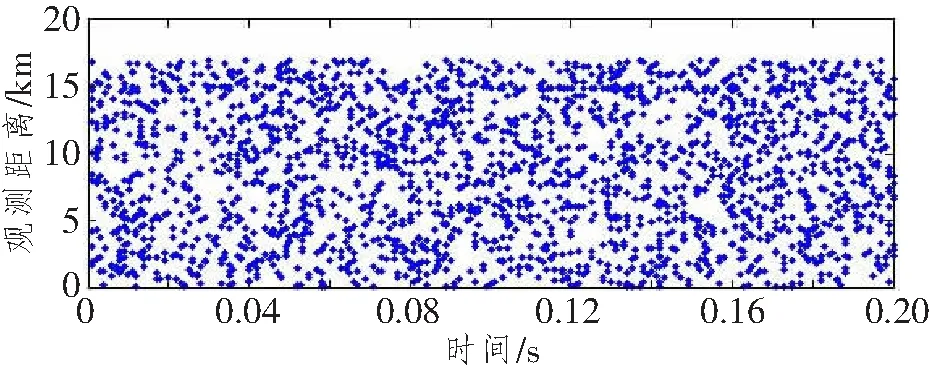
图1 200 ms内生成的回波事件Figure 1 Echo events generated within 200 ms
2 轨迹提取
在发射和接收脉冲之前,信号的接收者并不知道飞行器与目标的相对距离、速度以及加速度。因此,为了之后能够精确地跟踪目标相对于飞行器的运动轨迹,必须先积累一段时间得到飞行器初始运动状态的先验信息。
2.1 目标运动轨迹范围的确定
在接收到的回波数据中,信号一般分布在散点密集的地方,噪声则均匀分布在整个探测区域内。本文通过将N个周期内接收到的回波事件个数进行叠加找到回波数目最大的时刻(该时刻为接收机最后一次接收到回波的时刻),由此初步估计接收机接收回波光子信号的位置范围。
假设目标与飞行器的初始距离为15 km,飞行器以2 000 m/s匀速运动,积累的观测周期数目为500,每个周期为1 ms,理论上出现回波数目最多的个数在90 000 ns左右。
确定好了目标在积累时间段末的大致位置后,以数目最多的回波所在位置为基准,向前后各取一定距离的门宽(前门限到基准位置要远小于后门限到基准位置。为了不丢失信号,一般把后门限尽量设置大一些。),得到筛选出来的回波事件。
2.2 飞行器与目标相对距离的提取
由于接收到的回波事件是一群密集的散点,如图1所示,信号回波淹没在噪声[10]中,很难发现并提取出来。即使将每个周期的回波事件进行累加得到一条特征线(可以认为是随时间变化的飞行器和目标的相对距离,因为信号集中在某一个区域出现,而噪声只是均匀分布在整个区域),要想在散乱的点中直接提取这条曲线还是非常困难的。本文先用回波数据进行预处理得到目标运动的模型,在已知模型的基础上用随机抽样一致性(Random Sample Consensus,RANSAC)算法精确提取回波光子信号。
由于数据量比较大,本文首先采用常用的大数据处理方法莱特准则剔除部分无关紧要的数据。对于剩下的散点,将其分成若干个小区间后,通过统计每个区间的光子数目粗略提取目标轨迹的范围。每个周期内信号出现的概率总是大于噪声出现的概率,可以根据回波事件出现的个数提取回波光子。以横坐标为观测时间(时间间隔为一个周期),纵坐标为观测距离,建立平面坐标系。然后将这个平面分割成棋盘格类型的若干个小区间,对每个区间统计回波事件的个数Nij(i=1,2,…;j=1,2,…)。最后搜索并提取每列中Nij(j=1,2,3,…)最大的那个区间并用多项式对这些位置上的点初步拟合后得到目标与飞行器相对距离变化的轨迹方程,为下一步RANSAC算法提取回波光子提供初始的数学模型。
RANSAC[11-12]为一种稳健的模型参数估计算法。在一组包含异常数据的样本中,通过与数据相关的数学模型,给出有效的样本数据。RANSAC算法的假设是正确数据内点(inliers)可以被模型描述,而异常数据(outliers)则无法适应数学模型,可以认为是数据集中的噪声。数据预处理后,可以将轨迹方程当作先验数学模型,然后用RANSAC算法对模型进行优化并提取目标的相对运动轨迹。
在积累的时间段用RANSAC算法精确提取目标的相对运动轨迹后,就知道了飞行器相对目标的距离随着时间的变化规律,为后面的跟踪提供先验信息。具体的跟踪步骤如下:
(1) 根据积累时间段内目标的相对运动轨迹对后N(N的大小可调整)个周期预测目标的相对位置;
(2) 以每个相对位置为中心,取一定距离宽度的门构成波门;
(3) 取波门内距离波门中心最近的回波事件作为回波光子。如果波门内没有光子就将波门中心作为回波光子的位置。
(4) 将N个周期内得到的回波光子与前M(M的个数可调)个周期的回波进行最小二乘拟合,更新得到新的相对运动轨迹。重复以上过程直至跟踪完毕。
3 实验结果与分析
3.1 预测目标的先验信息
该仿真依据的实验样机的具体参数为:激光发散角α=1 mrad,空间目标雷达截面积为0.5 m2,激光波段为532 nm,Et=20 μJ,ρ=0.1,ηr=0.6,ηt=0.9,τ=1,D=60 mm。假设已知目标相对飞行器的初始距离为15 000 m,目标的相对速度为2 000 m/s,相对加速度为-10 m/s2,激光发射脉冲的周期T为1 ms,积累时间为500个周期。根据式(1)~(2)和式(6)计算出500个周期内飞行器接收回波光子的概率Psn(i)(i=1,2,3,…,500)的理论值,然后根据这500个概率按照1.4节所述的方式生成并筛选回波事件,如图1所示。
按照2.1节所述方法初步提取目标的相对运动轨迹范围后,按2.2节所述方法对回波散点数据进行预处理。将纵轴平均分成1 000份,横轴平均分成500份,生成50万个小区间Iij(i=1,2,…,1 000,j=1,2,…,500)。对每个区间内,统计该区域的回波个数为Nij(i=1,2,…,1 000;j=1,2,…,500)。提取每列Nij数目最大的区间作为回波光子所在的区域,如图2所示。

图2 均值滤波后的回波信号Figure 2 Echo signal after mean filtering
将这些点拟合得到目标运动轨迹方程,为下一步的RANSAC算法提供初始的数学模型。最后根据该初始模型,用RANSAC算法优化该模型并提取积累时间段内目标的相对运动轨迹,信号回波与目标理想运动轨迹的关系如图3所示。

图3 RANSAC算法提取目标运动轨迹Figure 3 Target trajectory extracted by RANSAC algorithm
3.2 根据先验信息跟踪运动的目标
跟踪从500 ms开始,跟踪周期500~510 ms的目标相对运动轨迹。图4所示为RANSAC算法优化回波点云后得到的目标运动轨迹。

图4 RANSAC算法预测的10个周期内目标运动轨迹Figure 4 Target trajectory predicted byRANSAC algorithm in 10 periods
图4中红圈为观测到的脉冲,由图可知,观测到的距离与预测的距离有一定差异。一般观测到的脉冲比较少,无法直接提取有用信息,需要使用部分旧脉冲作为补充重新拟合。此处取前面200周期(周期大小可以调整)即可,使用300~510周期的数据重新拟合,拟合后的结果如图5所示。
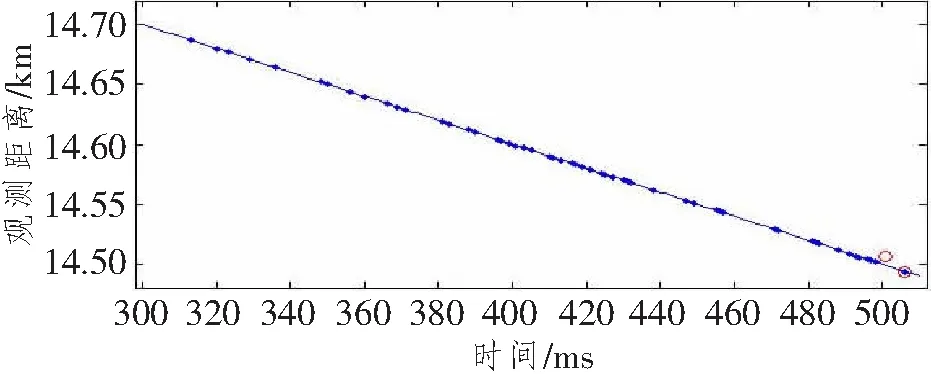
图5 300~510 ms回波点云重新更新的运动轨迹Figure 5 The trajectory within 300~510 ms after echo point cloud update
图5中蓝点是前一段时间积累的回波信息,红圈是新观测到的新回波信息。 图中倒数第2个点就是一个噪声脉冲,这时只需要将误差比较大的个别点剔除,再拟合即可。下一个大周期的跟踪按该方法执行,直到运动结束,最后得到的目标跟踪轨迹与理想目标运动轨迹的误差如图6所示。
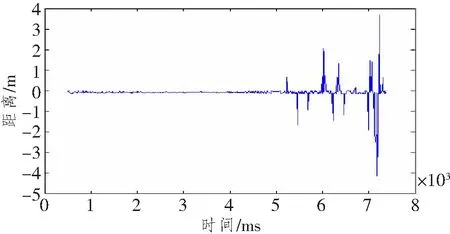
图6 目标理想相对运动轨迹与跟踪轨迹的误差图Figure 6 Error diagram of ideal relative Motion trajectory and tracking trajectory of target
由图可知,越往后跟踪误差越大。尤其是当飞行器的运动状态发生了突变,跟踪精度会大大下降。对于目标突变状况的跟踪,还需要建立特定的模型来实现。
4 结束语
本文模拟了光子探测激光测距对慢速运动(相对光速而言)目标的跟踪。根据实验所得的经验公式,用统计的方法生成了回波事件,然后将图像处理的相关算法运用到大量回波数据中提取目标的轨迹。仿真后得出目标的轨迹信息与目标理论的运动轨迹误差在5 m以内。光子探测激光测距能在较强的背景噪声条件下获得较高的定位精度,将其作为北斗导航系统的一个辅助定位模块会大大提升北斗导航系统定位的精确度。

