基于经验模态分解的发动机脉动压力数据分析

任春雷，周小陈，张炳诚，薛小龙，武艳奎，杨懿

（1.国防科技大学空天科学学院，湖南 长沙 410000；2.中国航天科工飞航技术研究院，北京 100074；3.中国航发北京航科发动机控制系统科技有限公司，北京 102200；4.北京控制与电子技术研究所，北京 100038；5.庞巴迪（天津）航空服务有限公司，天津 300300；6.北京航天试验技术研究所，北京 100074）

0 引言

在液体火箭发动机试验中，根据所测压力信号随时间的变化可分为稳态压力和脉动压力两大类。稳态压力的测量结果是压力平均值，用于研究试验台和发动机的性能。脉动压力则主要针对发动机推力室、泵、燃气发生器、推进剂管路等高压、高温、强振动测点进行脉动压力参数的测量与分析，其主要目的是研究发动机启动特性、不稳定燃烧、管路特性以及分析发动机的故障原因［1］。由于脉动压力测量与稳态压力测量在测量方法、测量系统构成和数据结构等方面有较大的差别。因此采用准确、有效的方法对脉动压力数据进行分析是非常重要的。

从时间域内压力变化趋势的角度进行分析，脉动压力与稳态压力最大的区别在于其变化时间序列具有非线性、随机性的复杂特征［2］。业内一般采用计算一段时间内的平均值或者观察某个时间点的压力值的方法对稳态压力数据进行分析。而对于高频采样下的高精度脉动压力数据，则不仅需要关注其在时域内的幅值信息，而且还需要根据信号时域和频域的特征，结合实际研究的需要，采用时频分析技术深度挖掘数据在时域和频域的特性信息。目前，在信号时频域分析技术领域，较为常用的方法有傅里叶变换、短时傅里叶变换、快速傅里叶变换和小波分析方法等等。这几种时频分析方法各具特点。

傅里叶变换和快速傅里叶变换方法建立了信号在时、频域的相互转换关系。通过绘制信号在频域内的全局图谱，可以清晰观察所分析的信号在时域内的频率-幅值特征。该方法的不足之处在于缺乏局域分析能力，即无法定位所得到的频率-幅值特性在时域内的发生时刻［3-4］。短时傅里叶变换的核心思想是将一个非线性信号看作若干个短的线性信号的集合，通过设定一个尺度不变的窗函数，将窗函数在时间轴上进行平移，以此来覆盖整个非线性信号，分析多个短信号局部的时间-频率信息。该方法的不足之处在于实际应用中需要根据信号的特征选择对应的窗函数，且分析效果取决于所选定的窗函数，分析的结果具有一定的不确定度性［5］。小波分析方法的实质是通过分析特定时间域内原始信号的特征，人为选定与之相匹配的基函数。将基函数在尺度上进行相应的伸缩，建立一个函数簇。将函数簇在指定的间域内进行多次平移，并对分解得到信息进行滤波等处理后进行重构，能够得到原始信号在时间域内局部特征信息。小波分析克服傅里叶变换不能兼顾时间和频率分辨力的缺点，具有局部自适应分析能力，在工程应用中得到了广泛的应用。其局限性体现在以下两点：首先，小波分析以傅里叶变换为基础，虽然提供了一个尺度可变的时间-频率窗，但是过度调整窗口的尺度会产生信息泄露的问题。其次，由于已经根据原始信号的特征人为选定了与之相匹配的基函数，且在后续的分析过程中无法进行更改，不同的小波基函数的分析结果往往是不同的［6-7］。

为满足精确描述频率随时间变化的需要，美籍华人科学家Norden E.Huang提出了一种新的信号处理方法：经验模态分解（empirical mode decomposition，EMD）［8］。该方法对于非平稳线性信号的分析具有非常好的效果，其核心思想是对非平稳线性信号进行平稳化处理，逐级分解信号中所包含的不同尺度下的波动或者变化趋势，将分解得到的一系列不同特征尺度的数据序列称之为本征模态函数（Intrinsic Mode Function，IMF）。对每一个IMF进行希尔伯特变换（Hilbert Transform，HT），从而得到不同特征尺度下的瞬时振幅和瞬时频率。该理论的创新之处在于定义了瞬时频率的概念，引进了EMD和IMF的概念。通过对IMF分量进行希尔伯特变换得到时频域的Hilbert能量分布频谱图，建立了谱分析与时域的对应关系，能够精确分析原始信号时频域的分布规律［9-10］。

汪伟等［11］针对跑步机用户进行行走速度估计过程中出现的加速度漂移问题，根据跑步机用户行走速度数据的特征，利用EMD方法在不同频率段内将摆动脚速度进行分解。通过选择与用户步频相近的频段，摒弃无关频段，并对本证模态函数进行重构，从而解决了加速度飘逸的问题。采用集成经验模态分解法对速度积分后得到的摆动脚位移进行分解与重构，有效解决了积分累积误差引起的模态混叠现象。徐可、李俊等［12-13］充分利用EMD方法在自适应分析方面的优势，采用将EMD分解后的本征模态函数所包含的能量特征和支持向量机（SVM）遗传算法相结合的方法对非平稳轴承振动信号处理进行分析处理，分析的结果表明该方法在识别和定位滚动轴承故障方面具有良好的效果。汪朝海等［14］利用EMD方法在主成分分析、信息提取和自适应分析方面的优势，对数据分析EMD分解。将IMF函数和残差函数组成的特征向量作为滚动轴承故障识别的主要特征。对振动数据的分析结果显示，与支持向量机、BP神经网络等算法相比，该方法在故障识别率、运行时间和操作便捷性方面更具有优势。杨建华等［15］对降噪后的滚动轴承故障数据进行EMD分解。通过对比分析轴承故障仿真信号和滚动轴承实验信号的之间的特性信息，能够对包含强噪声的滚动轴承数据进行故障分析和定位。晏红艳等［16］针对传统相干噪声压缩去噪法对含噪信号进行去噪过程中容易消除有效噪声的问题，结合多通道联合时频分析法，将含噪地震信号分解为多个频率段下的分量。利用EMD方法在特征信号提取和自适应分解方面的优势，在消除了含噪地震信号中噪声的同时也有效保存了原始信号中的有用信息。

本文针对发动机试验脉动压力数据的非平稳非线性特征，结合经验模态分解在自适应特征分析、瞬时频率的精确定位能力、局部瞬时表达能力以及提取信号分量等方面的优势，对某型号发动机试验的脉动压力数据进行分析。

1 脉动压力测量系统的基本组成

工程应用中，脉动压力测量系统具有频率响应快，采集系统采样率高的特征，能够精确测量推力室高温、高压和剧烈振动环境下的压力变化信息。测量系统一般由数采和分析系统、供电系统、脉动压力传感器、信号转换装置、循环冷却系统和信号转换装置等几个部分组成［8］，测量系统组成原理如图1所示。

图1 脉动压力测量系统组成原理图Fig.1 Schematic diagram of fluctuating pressure measurement system composition

脉动压力传感器的功能主要是完成脉动压力测点的测量，实现测点压力值到电信号的转换。传感器必须具有耐强振动、高温和高压的工作特性。脉动压力传感器的安装以及测压导管的长度等都有一定的要求［8］。

数采和分析系统主要完成数据的采集和分析，对其采样率和频响也有相应的要求，采集系统采样率一般大于等于10 kHz。

循环冷却系统主要功能是在传感器工作过程中通过水冷或者气冷的方式降低传感器内部环境的温度，保障传感器正常工作温度环境，延长工作寿命，提高系统可靠性。

2 经验模态分解的基本理论与优势

2.1 经验模态分解的基本理论

对于一个实信号x(t)，可以构建一个复信号z(t)，定义为［10］

式中：a(t)，θ(t)分别为实信号x(t)的瞬时幅值和瞬时相位。

瞬时频率等于瞬时相位的导数，即

令EMD分解得到的IMF分量为hi(t)，对其进行希尔伯特变换为

根据公式构造解析信号

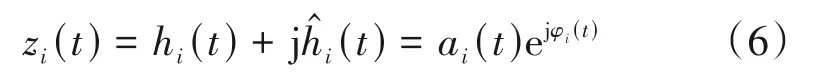
则幅值函数为

式中：ai(t)为解析信号的瞬时幅值；φi(t)为解析信号的瞬时相位。

瞬时频率为

希尔伯特谱为

希尔伯特边际谱为

式中：T为所分析原始信号的总时长。从式（9）可知，希尔伯特谱能够在时、频域内精确描述信号的幅值的变化规律。

工程应用中对EMD分解后的征模态函数（IMF）分量进行HT变换时，IMF分量在数学上需要满足时间历程中极值点个数和过零点个数相等或者相差1个和局部极大值、极小值相加的均值为0的要求［17］。虽然IMF函数能够合理地反映信号内部在每一个周期上的波动性，但是并非在所有情况下满足上述要求的IMF函数都能够计算出瞬时频率。其主要的原因在于工程应用中原始信号往往较为复杂。真实信号中包含大量不相关的噪声分量使得原始信号中包含多个振动模态分量。针对该问题，Huang和相关研究人员对IMF函数及相应原始信号的特征进行了研究和修订，提出符合对信号进行EMD分解及对IMF函数进行HT变化的原始信号需要满足以下假定条件［17］：①原始信号至少包含一个极大值点和一个极小值点；②相邻两个极值点之间的时间间隔为特征时间尺度；③对于信号中无极值点，仅有拐点的情况，采用对信号进行微分的方法获得极值点。

EMD分解的步骤主要分为：

1）定位x(t)中所有极大值点和极小值点。采用三次样条插值法绘制x(t)的上下包络线（极大值点形成上包络线，极小值点形成的下包络线）。计算上、下包络线的均值m1。x(t)与m1的差记为h1，即

将h1作为新信号x(t)，重复式（11）的步骤。直至所得到的分量hi满足IMF函数的基本条件［17］时，将满足条件的第1个一阶IMF分量称之为C1，C1包含信号中的最高频成分。

2）将一阶IMF分量C1从x(t)中分离出来，令剩余的原始信号为r1，令

将r1作为新信号，重复步骤1），直到第n阶的残余信号成为单调函数。

3）数学上x(t)可视为n个IMF分量和一个残余分量的和，即

式中：rn(t)为信号中的残量。各IMF分量Cj(t)则代表了信号中所包含的所有不同高、低频率的成分。

在实际操作过程中需利用计算机编程完成信号的EMD分解过程。分解流程一般如图2所示。

2.2 经验模态分解的优势

2.2.1 自适应时频分析

从2.1章节的基本理论可知，EMD理论建立了瞬时频率的物理意义。通过将原始信号分解为多个IMF分量，对各IMF分量进行HT变换得到原始信号在时、频域的希尔伯特谱。瞬时特征量精确定位了希尔伯特谱在时频域的特征。相较传统的时频分析方法，EMD方法的优点在于定义了一组根据原始信号特征而制定的具有自适应分解特性的基函数，从而使该方法在实际应用中具有良好的自适应分析优势。

2.2.2 信号局部瞬时特征表征

根据2.1章节的理论可知，通过给出瞬时频率的定义，即对EMD分解过程中所得到的多个IMF分量的相位进行求导，能够从物理意义层面对瞬时频率在局部瞬时特性方面的优势进行清晰、明确地说明。相较传统傅里叶变换在频率混叠、虚假谐波方面的缺陷，EMD分解中多个IMF分量从高阶到低阶的排序也有效解决了上述问题。多个IMF分量瞬时频率相位求导的方法则体现了该方法具有对原始信号的局部特征进行精确描述的能力。

2.2.3 主成分分析

在工程应用中，复杂的非线性非平稳随机信号往往包含了大量真实信号和各种不相关的噪声分量。对复杂信号进行分析的重要目的是将复杂原始信号中有价值的真实信号提取出来。从2.1章节的介绍可知，EMD方法能够将原始信号中的频率分量按照从高到低的顺序分离提取出来以满足信号分析的需要。数据分解的结果能够较好地体现各频率分量在原始信号中的比重。因此，该方法也是一种能够对复杂信号进行主成分分析、提取的重要工具。

3 实例分析

3.1 脉动压力数据特征

基于脉动压力测量系统高频响、高采样率的特性，脉动压力数据具有采样率高、数据容量大的显著特征［18］。某型号发动机试车中，按照图1组建脉动压力参数测量系统。传感器采用Kulite-CT-375水冷型脉动压力传感器。传感器的性能参数和计量机构检定结论分别如表1、表2所示。

表1 CT-375型传感器性能参数Tab.1 Performance parameters of CT-375 sensor

表2 CT-375型传感器检定结果Tab.2 Verification results of CT-375sensor

推力室脉动压力参数名为Pis1，脉动参数采集系统的采样率为10 kHz。选取试车中稳定段0.2 s（2000个样本点）的数据进行分析。试验全程脉动压力数据如图3所示。相邻测量部位稳态压力测量数据如图4所示。测点名：Pcio1，稳态参数采集系统的采样率为1 kHz。由于脉动压力测点和稳态压力测点分属不同的测量系统，所用数据采集设备不同，故二者在坐标轴上显示的时间有所区别，但发动机总工作时间是相同的。

从图3和图4可知，脉动压力测点数据和稳态压力测点数据在波形变化趋势上基本一致，印证了测量数据的合理性。相较高采样率、高精度脉动压力测量系统，稳态压力测量系统的测量数据在波形上较为光滑。而脉动压力测量系统凭借高采样率、高频响和高测量精度的优势，能够非常精确地捕捉到推力室内压力的波动变化情况。

图3 某型号发动机试验脉动压力全程数据图Fig.3 Full range data diagram of fluctuating pressure of a certain type of engine test

图4 某型号发动机试验稳态压力全程数据图Fig.4 Full range data diagram of steady-state pressure of a certain type of engine test

脉动压力数据稳定段0.2 s和0.02 s局部数据分别如图5和图6所示。图5中，在发动机试车稳定段26.10～26.30 s内，推力室压力在8.614～8.911 MPa之间震荡波动，变化范围达到0.297 MPa。图6清晰地显示了推力室内压力突变的情况，具有高采样率特征的脉动压力测量数据在精确描述推力室内脉动压力在时域内波动情况的同时，也为工程技术人员采用多种时频分析方法对其进行分析奠定了重要的基础。

图5 发动机试验脉动压力局部数据图1Fig.5 Local data diagram 1 of engine test fluctuating pressure

图6 发动机试验脉动压力局部数据图2Fig.6 Local data diagram 2 of engine test fluctuating pressure

3.2 数据分析

根据2.1章节的理论基础和方法，对稳定段26.10～26.30 s内的脉动压力数据进行经验模态分解，分解结果如图7所示。

图7 EMD分解结果图Fig.7 EMD decomposition result

从图7中EMD分解结果可知，采用EMD分解方法能够将脉动压力数据中的频率分量分离出来。IMF1～IMF4阶分量分别显示了脉动压力数据所在时域内所包含的频率成分以及幅值相对大小。其中IMF1阶分量在原始信号中所占的比重最大，频率分量最高。IMF2～IMF4阶分量在原始信号中所占比例逐渐降低。IMF2，IMF3和IMF4分量的幅值波动趋势要大于IMF1分量的幅值波动。R主要为系统中的一些其他不相关低频分量，变化过程非常缓慢且无规律，对数据的分析基本无影响。

对IMF函数进行HT变换的希尔伯特谱如图8所示。

图8 IMF1～IMF4时间频率曲线图Fig.8 IMF1～IMF4 time frequency curve

由图8可知第1层～第4层时间-频率曲线非常清晰准确地显示了全时间域内频率的变化情况。在第1，2层中，3500～5000 Hz左右的中频带是数据的主要组成成分，1500 Hz以下的低频带所占的比重较少。第2，3和4层时间-频率曲线频率值变化情况显示在该时域内0.03，0.048，0.155和0.188 s存在多个频率值突变。结合推力室上下游相应的温度、压力测点、试验时序和试验工况等信息，对于分析判断推力室内燃烧状态具有非常重要的作用。

对分解得到的IMF分量进行重构后的时间-幅值特性曲线如图9所示。脉动压力数据的FFT频谱分析图如图10所示。

结合图5、图8、图9和图10进行分析可得到以下几点结论：

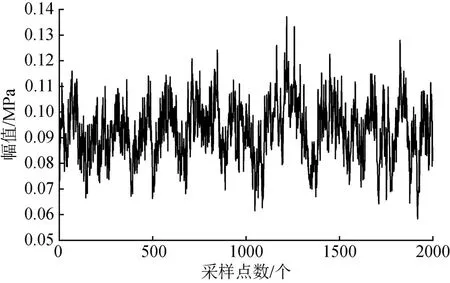
图9 EMD重构时间-幅值图Fig.9 EMD reconstruction time-amplitude diagram

图10 FFT频谱分析图Fig.10 FFT spectrum analysis diagram

1）通过对比图5与图9可知，图9中重构后的时间-幅值特性曲线相比原始数据具有更高的分辨力，能够更加清晰地分辨时间域内的幅值波动情况。不仅可以清晰分辨脉动压力周期性波动的情况，而且可以精准定位在0.12，0.18 s的幅值振荡。说明在该试车的稳定段内，随着推进剂燃烧对压强振荡响应，燃烧产生的能量持续注入燃烧室工作系统引起脉动压力有规律地振荡。通过对比同时段推力室对应的振动测点的振动数据，脉动压力有规律的振荡在振动数据中也得到了体现。此外，根据EMD分解的特点，针对涡轮泵、燃发器等振动剧烈的测点，还可参考文献［8］，［18］中的方法，结合相应振动测点的数据进行分析。

2）图8中第1层和第2层的时间频率特性曲线与图10中FFT分析结果相吻合。图8中第3层～第4层时间-频率特性曲线非常清晰地显示了低频分量的变化相对较缓慢的特性，也能非常清晰定位对应的变化时间点。

3）由图10中FFT分析结果可知，全时域内幅值峰值多集中在低频区（0～2000 Hz）和中频区（3500～5500 Hz）。这与图8中EMD分解时间-频率曲线的结果相吻合。但FFT的不足之处是分析结果只能显示全时域数据在频域内的信息，无法定位某个幅值峰值所发生的时间信息，也无法分析信号中的各频率成分。

分别采用Haar小波和Db9小波对脉动压力数据进行7层分解的结果如图11至图14所示。

图11 Haar小波5～7层分解细节系数图Fig.11 Detail coefficient diagram of Haar wavelet 5～7 level decomposition

图12 Haar小波1～4层分解细节系数图Fig.12 Detail coefficient diagram of Haar wavelet 1～4 level decomposition

图13 Db9小波5～7层分解细节系数图Fig.13 Detail coefficient diagram of Db9 wavelet 5～7 level decomposition

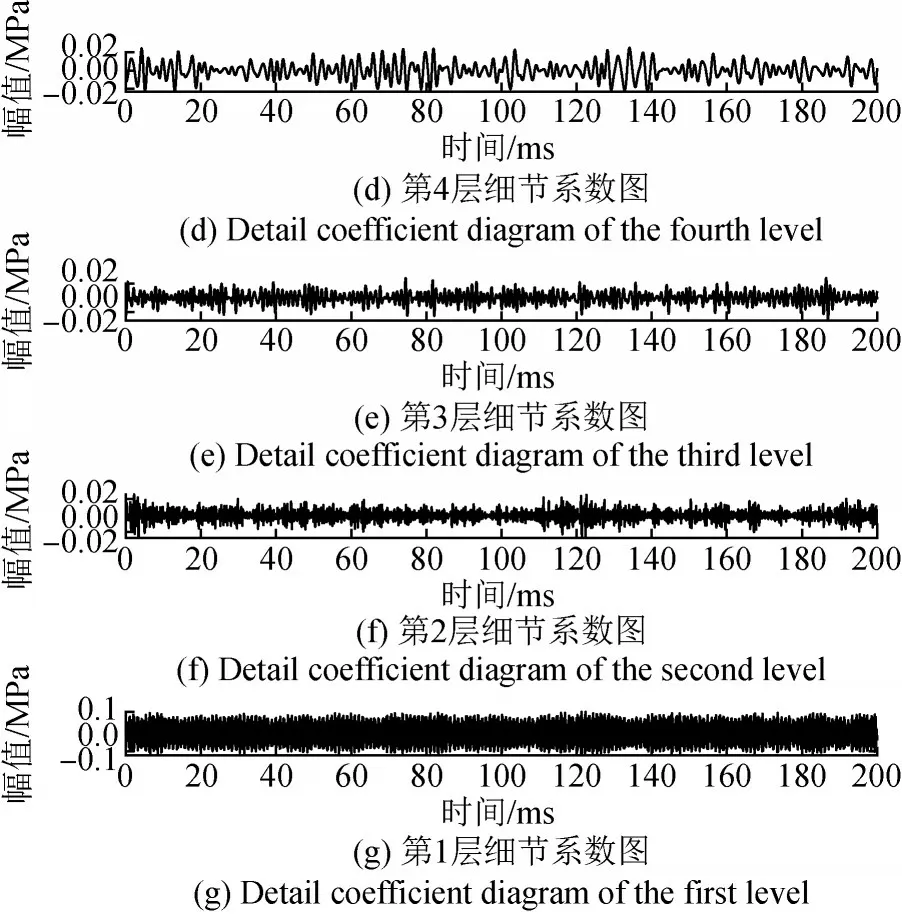
图14 Db9小波1～4层分解细节系数图Fig.14 Detail coefficient diagram of Db9 wavelet 1～4 level decomposition

由小波分析图11至图14可知，小波分析的结果与所选小波基函数有关（文献［18］介绍了多种小波基函数的特征）。由于Haar小波具有紧支撑、单个矩形波、矩形状阶梯变化等特征，分解得到的多层细节分量具有矩形特征，尤其是d4～d7层细节信息尤为明显。而Db系小波具有对称性好、频域的局部化能力强和消失矩光滑性好等特点，分解得到的多层细节分量的光滑性较好。d1～d5层分解信号中均能定位原始信号中幅值产生突变的时间信息。d6～d7层的分解结果均因分解层数高，过滤掉了过多的有用信息而存在一定程度的失真。小波分析的结果可以结合相应的振动测点数据，进一步分析所测部件的动态特性［8］。小波基函数的选择与分解层数的差异导致小波分析所得到的结果存在一定的差异，也给准确分析数据特征带来了困难。

4 总结

本文介绍了型号发动机试验中脉动压力测量系统的组成和数据特征。分析了采用传统傅里叶变换、小波分析等方法对非线性非平稳随机数据进行时频分析的缺点和不足。重点介绍了EMD的基本理论。从自适应时频分析、局部瞬时定位分析和信号主成分特征分析和提取三个方面介绍了该理论的优点以及实际工程应用的详细步骤。分别采用FFT方法、基于不同小波基函数和分解层数的小波分析方法和EMD分解方法对某型号发动机试验脉动压力数据进行分析。对比分析了FFT方法和小波分析方法对非平稳非线性数据的不足。脉动压力数据的EMD分解结果显示该方法能够非常清晰地自适应分离原始信号中的高、低频分量，显示数据在时间-频率域的多维特征。该方法可以与其他数据分析方法相结合，为产品型号设计和试验人员分析非线性非平稳型数据提供重要的参考依据，具有重要的参考和推广价值。