黄河流域工业生态效率研究
赵佳茹,田贵良,2
(1.河海大学 商学院,江苏 南京 211100;2.江苏长江保护与高质量发展研究基地,江苏 南京 210098)
生态效率即增加的价值与增加的环境影响的比值,由国外学者Schaltegger 等[1]于1990 年提出,得到世界可持续发展工商业联合会(WBCSD)等国际组织的认可并对其定义进行完善[2],国内有关学者把其作为衡量经济可持续发展、绿色竞争力的重要指标[3-5]。生态效率的已有研究主要从评价指标体系、测度方法、时空变化及影响因素等方面展开。 测度方法有单一比值、数据包络分析(DEA)、非径向超效率模型(SESBM)等,其中:DEA 可解决多投入多产出等复杂问题,是衡量生态效率的常用方法之一[6-7];SE-SBM 在DEA 基础上克服了径向有偏、难以处理无效决策单元、测算结果不可靠等问题[8-12]。 关于生态效率时空变化研究,大都从演化趋势和空间差异两方面入手,采用空间数据模型、局部空间自相关模型、LISA 集聚图等开展研究[13-15]。 关于生态效率影响因素研究,有关学者采用的方法有广义矩法、可拓展的随机性环境影响评估模型、双自助抽样截断回归模型、层次分析与聚类分析法等[16-20]。 上述关于生态效率的研究中,针对黄河流域工业生态效率的很少,为了丰富对黄河流域工业生态效率的评价研究、给黄河流域高质量发展提供参考,笔者以黄河干流沿线35 个地级市为样本市、以技术效率表征黄河流域工业生态效率,基于SESBM 模型进行2008—2018 年黄河流域工业生态效率测算、纯技术效率和规模效率分解,通过核密度估计、空间计量模型回归等探究黄河流域工业生态效率的时间演化趋势和空间分异特征、空间自相关性及其主要影响因素。
1 样本数据与研究方法
1.1 样本市选择及数据来源
选择沿黄河干流分布的35 个地级市(包括:青海西宁市,甘肃兰州、白银市,宁夏银川、石嘴山、吴忠、中卫市,内蒙古呼和浩特、包头、乌海市,山西太原、临汾、运城、忻州、吕梁市,陕西延安、西安、榆林、渭南市,河南郑州、开封、洛阳、焦作、新乡、三门峡、濮阳市,山东济南、淄博、东营、德州、滨州、泰安、济宁、菏泽、聊城市)作为样本市,其分布情况见图1。
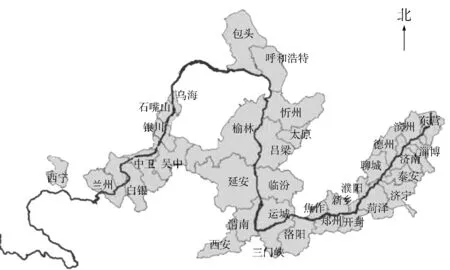
图1 样本市分布情况
参考相关文献,本研究以各样本市工业生产总值为期望产出,以工业废水排放量、工业二氧化硫排放量、工业烟粉尘排放量为非期望产出,以工业固定资产投资额、工业年末从业人数、工业用水总量为投入要素,采用SE-SBM 模型测度工业生态效率。 以2008—2018 年为研究时段,为消除价格变动的影响,以2008年为基期采用平减法对工业生产总值和工业固定资产投资额进行处理。 研究所用数据来源于《中国城市统计年鉴》、国泰安数据库,及各省(区)统计年鉴、水资源公报等,个别年份的缺失数据通过估算加以补充。
1.2 研究方法
1.2.1 SE-SBM 模型
SE-SBM 模型形式如下[21]:

参考曾贤刚等[22]、李在军等[23]对环境效率、生态效率的分级方法,对工业生态效率进行分级:ρ<0.5 为低效率,0.5≤ρ<0.8 为中低效率,0.8≤ρ<1 为中高效率,ρ≥1 为高效率。
1.2.2 核密度估计
核密度估计(KDA)是探究指标分布形态的非参数检验方法,运用KDA 可以得到黄河流域工业生态效率的概率分布曲线及演化轨迹。 核密度计算公式如下:
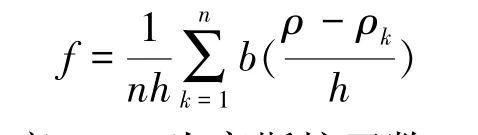
式中:f为核密度;b( )为高斯核函数;h为核函数的带宽,不同带宽的核密度估计值存在差异,h较小时核密度曲线较为曲折,h较大时核密度曲线较为光滑。
1.2.3 莫兰指数
构建基于反距离权重和经济距离权重的嵌套式空间权重矩阵,计算工业生态效率的全局莫兰指数和局部莫兰指数,对工业生态效率进行空间自相关性检验。莫兰指数值域为[-1,1],其值大于0 表明研究对象空间正相关,即高值与高值相聚或低值与低值相聚;小于0 表明研究对象空间负相关,即高值与低值相聚;等于0,则研究对象不存在空间自相关性。 莫兰指数计算公式如下:

1.2.4 SAR 空间计量模型
为解决传统面板回归模型未考虑空间异质性和拟合回归精度较低等问题,在面板回归模型的基础上考虑空间要素,建立如下形式的SAR 空间计量模型(对数据进行对数化处理以减小异方差):
lnρit=θωilnρt+βlnXit+ε
式中:ρit为地级市i、年份t工业生态效率;ωi为地级市i的权重;θ为相邻地级市工业生态效率作用程度;ρt为年份t黄河流域整体工业生态效率;Xit为地级市i、年份t影响因素;β为回归系数;ε为随机误差。
2 结果与分析
2.1 工业生态效率测度结果
按照上述方法计算的2008—2018 年黄河流域工业生态效率见表1。 从宏观上看,黄河流域工业生态效率整体上呈波动上升态势,从2008 年的0.561 上升至2018 年的0.896,由中低效率转变为中高效率。 分阶段看,工业生态效率呈现N 形上升态势,2008—2011年年 均 提 高0.040,2011—2013 年 年 均 下 降0.042,2014—2018 年年均提高0.060。 研究时段中期工业生态效率“断崖式”下降的原因可能是金融危机爆发后我国经济受到一定冲击,各地工业长期粗放式的发展模式对生态造成了一定程度的破坏,流域经济快速增长的同时伴随着高污染、高耗能,因此生态效率下降。
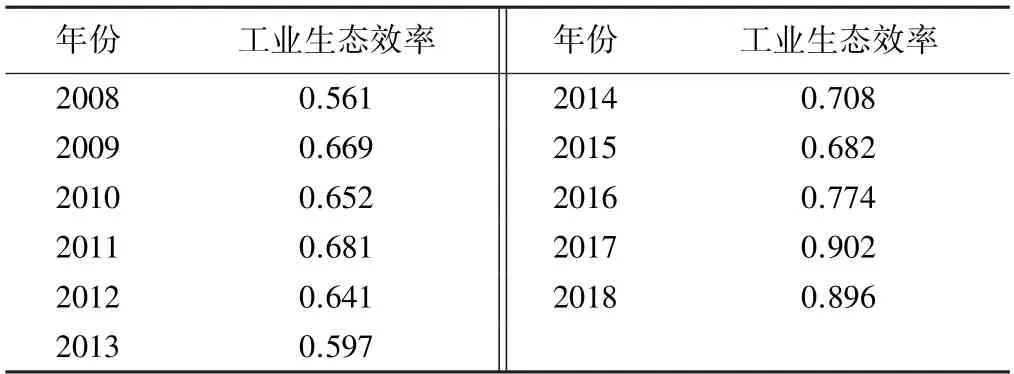
表1 2008—2018 年黄河流域工业生态效率
各地级市2008—2018 年多年平均工业生态效率、纯技术效率、规模效率见表2。 从微观层面看,各地级市多年平均工业生态效率空间分异显著:太原、呼和浩特、包头、延安、西安、榆林、东营等7 个地级市的工业生态效率≥1,属于高效率;白银、吴忠、忻州、渭南、新乡等5 个地级市的生态效率<0.5,属于低效率;工业生态效率最大值1.437(东营市)是最小值0.388(新乡市)的3.7 倍,表明生态资源与工业经济匹配度较低。观察各地级市纯技术效率和规模效率可知:纯技术效率为高效率的地级市有11 个(占地级市总数的31.4%)、为低效率的地级市仅有1 个,规模效率与纯技术效率相反,规模效率为高效率的地级市只有1 个、为低及中低效率的地级市有13 个(占比为37.1%)。
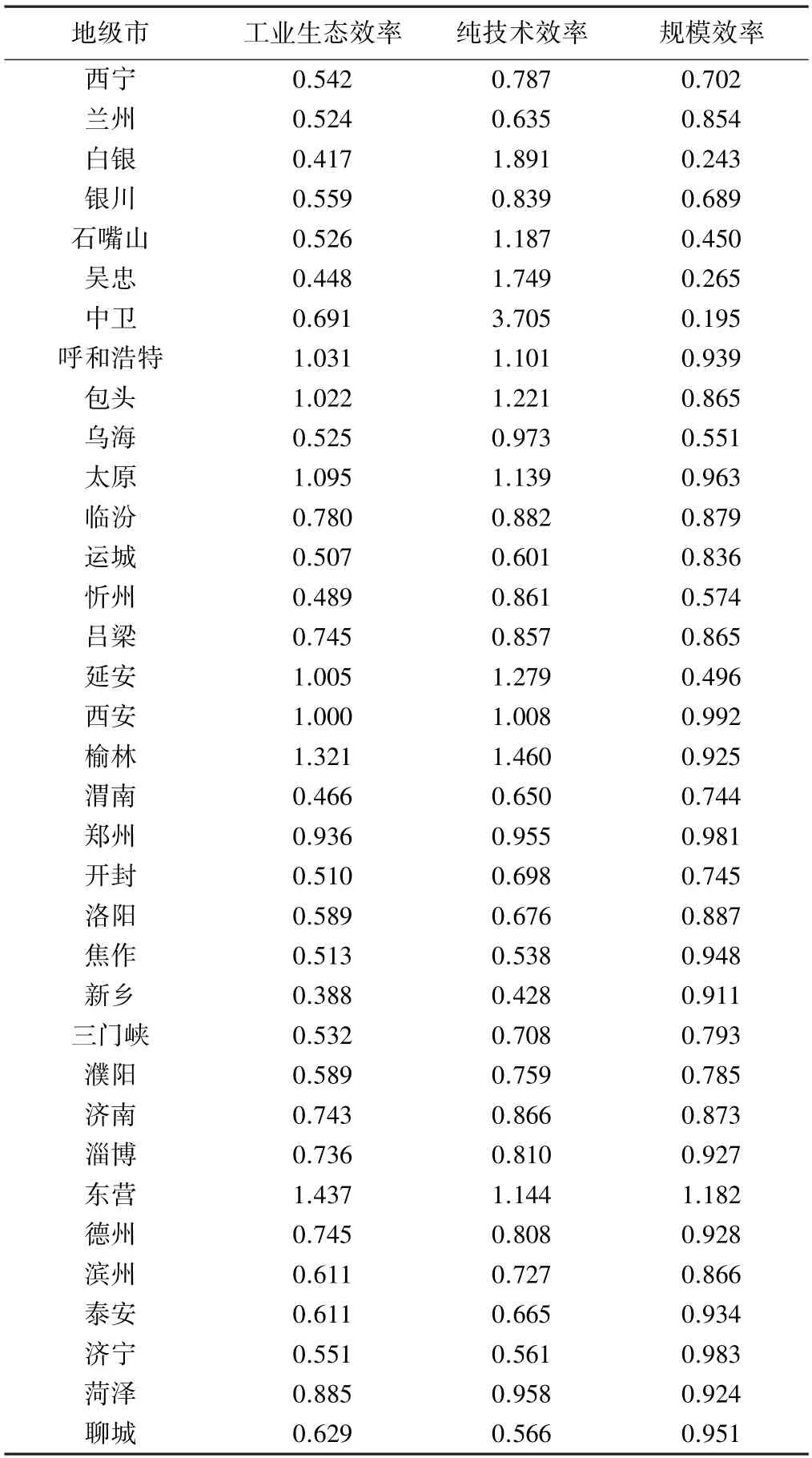
表2 各市多年平均工业生态效率、纯技术效率与规模效率
2.2 工业生态效率时空演化情况
2.2.1 时间演化趋势
选取2008 年、2012 年和2018 年3 个代表年份绘制的黄河流域工业生态效率核密度曲线见图2,可以看出:随着时间的推移,核密度中心呈右移趋势,2008—2012 年右移幅度较小、2012—2018 年右移幅度较大,表明黄河流域工业生态效率呈上升态势,经历了由缓慢提升到高速提升的过程;同时,核密度曲线在2008 年为双峰、到2012 年和2018 年变为单峰,峰高逐渐下降、跨度逐渐加大,表明黄河流域工业生态效率区域差异逐步加大。
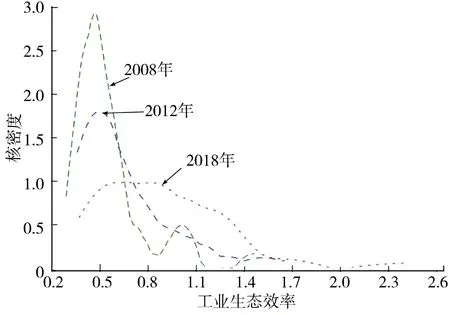
图2 代表年份工业生态效率核密度曲线
2.2.2 空间分异特点
把青海、甘肃、宁夏3 个省(区)作为上游区域(本研究不涉及四川省),把内蒙古、山西、陕西3 个省(区)作为中游区域,把河南、山东两省作为下游区域,统计各区域逐年工业生态效率均值,见表3。 选取2008 年、2012 年、2015 年、2018 年4 个代表年份,按自然断点法把各地级市工业生态效率分为4 个等级,其空间分异情况见图3。 由表3、图3 可知:2008 年和2012 年低效率地级市较多且集中分布在上游区域,中游区域效率最高,下游区域各地级市效率差异较大;2015 年和2018 年上游区域的中卫市迈入高效率行列,中游区域多数地级市仍处于高效率状态,下游区域工业生态效率比较稳定。 整体来看,中下游区域工业生态效率高于上游区域的。
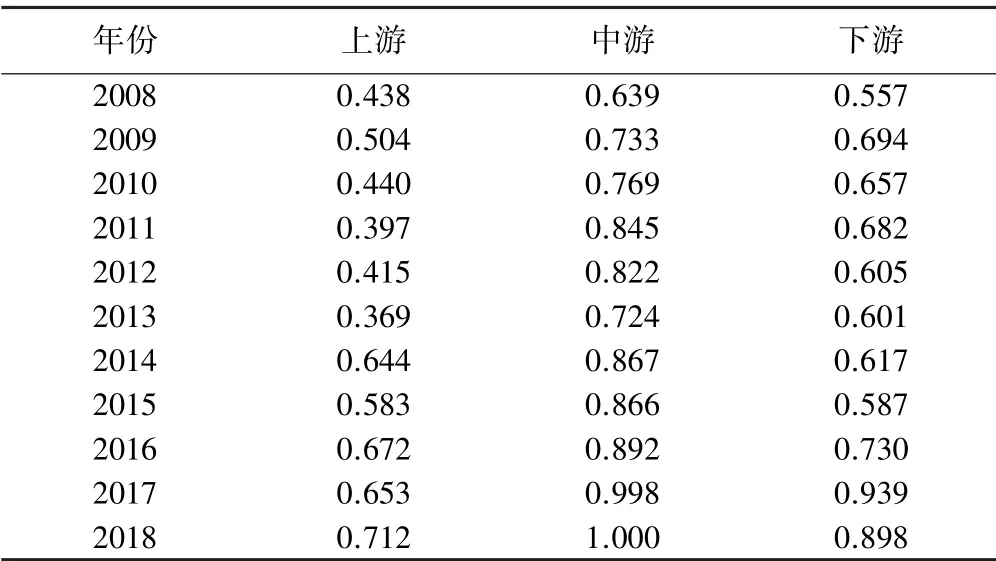
表3 各区域逐年工业生态效率均值

图3 典型年份工业生态效率空间分异情况
2.3 基于莫兰指数的空间相关性检验
2008—2018 年黄河流域工业生态效率全局莫兰指数见表4。 由表4 可知,黄河流域工业生态效率全局莫兰指数除2016 年和2018 年为负外其他年份均为正,各年份的空间相关性均达到10%的显著性水平,表明各地级市工业生态效率存在显著的正向空间集聚效应。
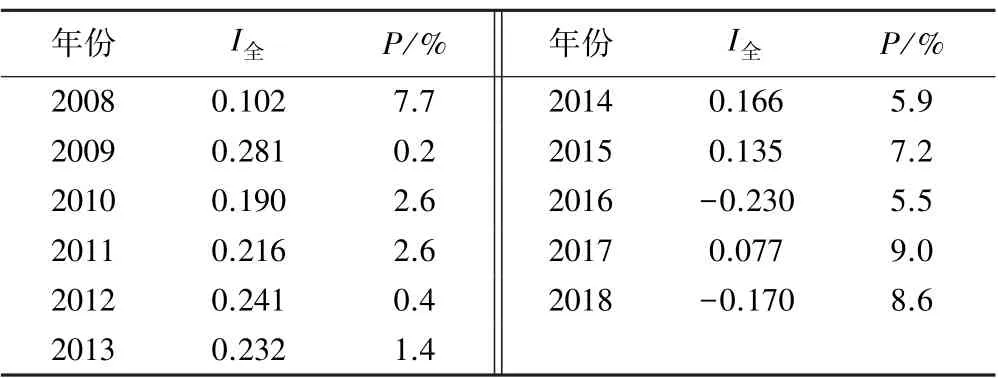
表4 工业生态效率全局莫兰指数及空间相关显著性水平
依据局部莫兰指数计算结果,点绘各年份莫兰散点图(图略)表明,黄河流域各地级市工业生态效率呈现高高集聚和低低集聚的空间分布特征,即各地级市工业生态效率具有正向空间集聚效应,但这种正向空间集聚效应呈逐年弱化态势。
2.4 工业生态效率影响因素
基于“绿水青山就是金山银山”的理念,构建生态保护、创新开放、民生保障、产业转型、社会保障等5 个维度的工业生态效率影响因素指标体系,见表5。
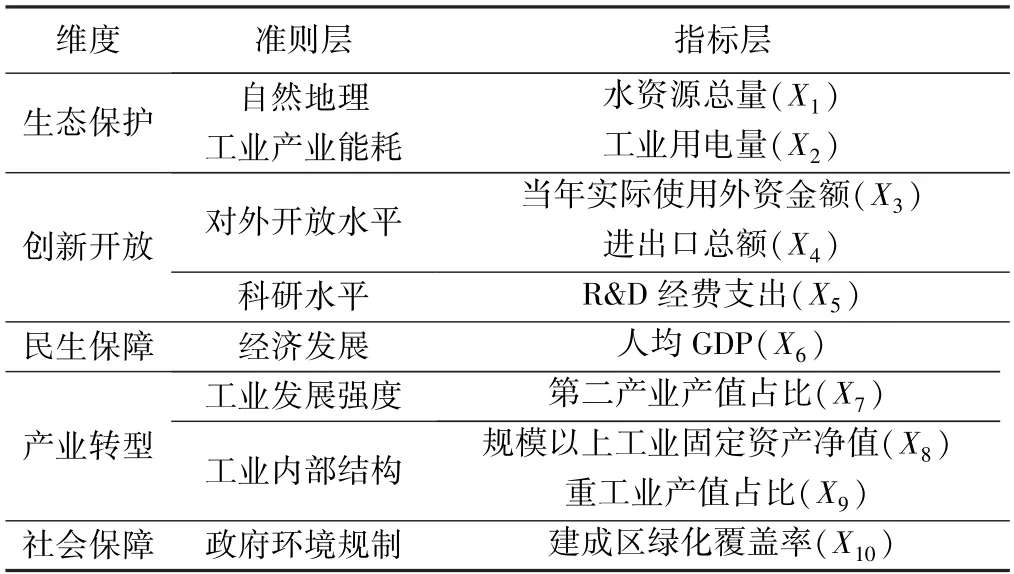
表5 工业生态效率影响因素指标体系
经LR、LM、Hausman 检验及联合显著性检验,选取固定效应的SAR 空间计量模型进行影响因素分析,即分别进行个体固定、时间固定与双向固定3 种效应模型回归。 结果表明,黄河流域工业生态效率回归系数为-1.076,达到了极显著水平,即黄河流域工业生态效率随时间变化呈负向溢出效应、各地级市工业生态效率对周边市工业生态效率有极显著负向影响,这一结果解释了上述空间正向集聚效应逐渐弱化的原因。由各指标回归系数及显著性(见表6)可知,大部分指标的直接效应(回归系数的绝对值)大于间接效应的,表明工业生态效率受本市有关因素的影响大于周边市有关因素的影响。
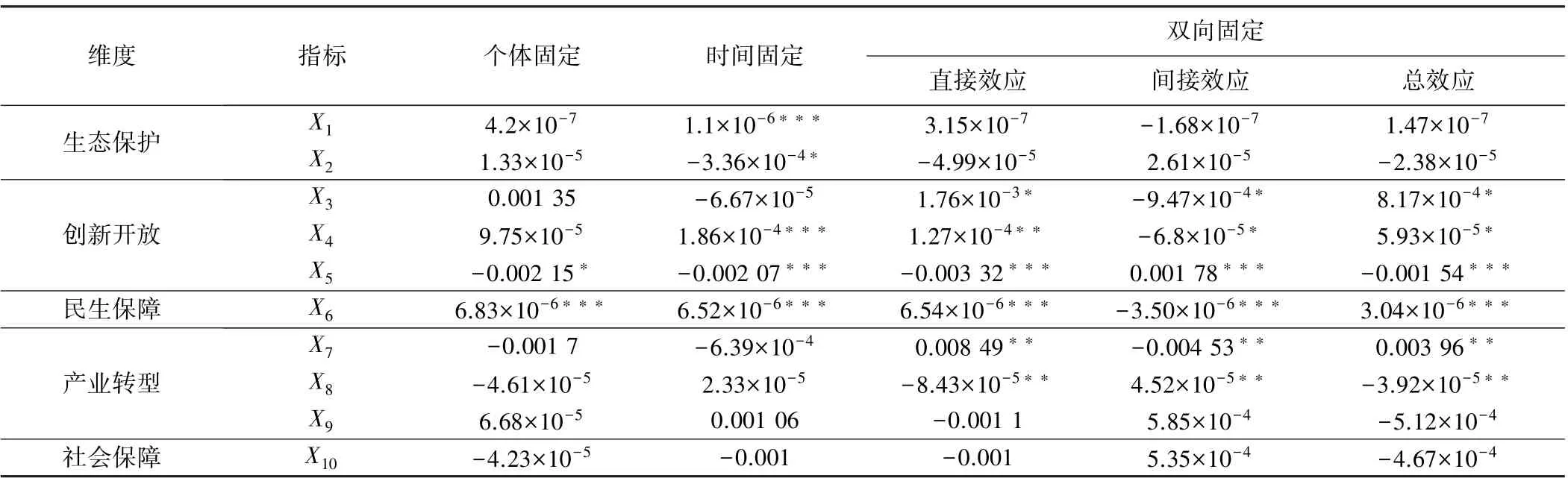
表6 工业生态效率影响因素回归系数及显著性
从生态保护维度看,水资源总量(X1)促进了本市工业生态效率的提升,但抑制了周边市工业生态效率的提升,其可能的原因是水资源为本市工业发展提供了条件,使得本市工业生态效率得到提升,但随着水资源利用量的增大,环境污染等负向效应逐渐抵消水资源对周边市带来的正向效用,使得周边市的环境治理成本提高;工业用电量(X2)对本市工业生态效率有负向效应,但不显著。
从创新开放维度看,当年实际使用外资金额(X3)和进出口总额(X4)与本市工业生态效率正相关、与周边市工业生态效率负相关,可能原因是资本的逐利性,外资总量有限且通常集中于发展潜力较大的城市,对周边市工业生态效率的提升作用甚微;R&D 经费支出(X5)与本市工业生态效率极显著负相关、与周边市工业生态效率极显著正相关,这一回归结果与实际情况似不符,其原因可能是科研与技术创新水平较低且效应滞后和科研经费投入的低效性。
从民生保障维度看,人均GDP(X6)与本市工业生态效率极显著正相关、与周边市工业生态效率极显著负相关,说明本市工业经济的高速发展在提高居民生活水平的同时激发了劳动者的工作积极性并吸引外部人才流入,长此以往有助于工业生态效率的提升。
从产业转型维度和社会保障维度看,第二产业产值占比(X7)与本市工业生态效率显著正相关,表明工业产业结构的转型升级有利于本市工业生态效率的提升,这一结果与姚愉芳等[24]的研究结果一致;规模以上工业固定资产净值(X8)和重工业产值占比(X9)与本市工业生态效率负相关、与周边市工业生态效率正相关,表明其抑制了本市工业生态效率提升、有利于提升周边市工业生态效率;建成区绿化覆盖率(X10)与本市工业生态效率负相关、与周边市工业生态效率正相关,理论上讲,建成区绿化覆盖率的提高会促进本市工业生态效率的提升,而回归结果与之相悖,这与上述黄河流域科研与技术创新水平较低且效应滞后的情况类似。
综上所述,黄河流域各地级市不仅要加强产业结构合理调整、对外开放等,而且还应加强与周边城市的科研合作,提升区域创新活力及其效应。
3 结论与建议
3.1 结 论
以黄河干流沿线35 个地级市为样本市,运用SESBM 模型测度黄河流域工业生态效率,并通过核密度估计、空间计量模型回归等分析其时空演化情况及影响因素,得到以下结论。
(1)从宏观层面看,黄河流域工业生态效率2008年为0.561、2018 年为0.896,研究时段内由中低效率稳步上升为中高效率,其主要受纯技术效率上升的拉动,而规模效率上升的作用相对较小;从微观层面看,各地级市工业生态效率空间差异显著,最大值是最小值的3.7 倍,表明生态资源与工业经济匹配度较低。
(2)黄河流域工业生态效率时间演化趋势是在波动上升的同时空间差异逐步加大,空间分异特点是中下游地区高于上游地区,由高到低顺序为中游地区、下游地区、上游地区。
(3)黄河流域各地级市工业生态效率存在显著的正向空间集聚效应,即呈现高高集聚和低低集聚的空间分布特征,但这种正向空间集聚效应呈逐年弱化态势。
(4)在工业生态效率的众多影响因素中,R&D 经费支出、规模以上工业固定资产净值抑制本市工业生态效率提升、促进周边市工业生态效率提升,人均GDP 促进本市工业生态效率提升、抑制周边市工业生态效率提升,而水资源总量对工业生态效率的影响不显著。
3.2 建 议
(1)各地级市应根据自身条件因地制宜制定工业生态效率提升策略,如:东营等工业生态效率较高的地级市可借助自身经济发展优势,继续加强工业高新技术研发,实施工业生态化建设;白银、吴忠等工业生态效率较低的地级市可借助优良的生态环境,合理调整产业结构、承接优势工业产业,尽快提升工业生态效率。
(2)各区域应破除行业壁垒和行政区划壁垒,强化彼此间的协同治理联系,搭建黄河流域生态经济一体化合作桥梁。 工业生态效率较低的区域要突破“信息孤岛”的桎梏,加强区域间工业信息的交融与互动;工业生态效率较高的区域要保持良好发展势态,辐射、带动周边区域提升工业生态效率,促进黄河流域工业产业由“单核心”向“多核心”共赢局面发展。

