再探拿破仑三角形——由一道模考题说起*

蔡晓波 邱志权 (广东省中山市桂山中学 528463)

1 问题背景

·试题与评析

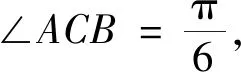
评析本题以拿破仑定理为背景，考查学生对基本不等式、解三角形等相关知识的掌握情况，该题图形具有很好的几何对称美(图1)，可让学生充分感受到数学的美与巧妙．

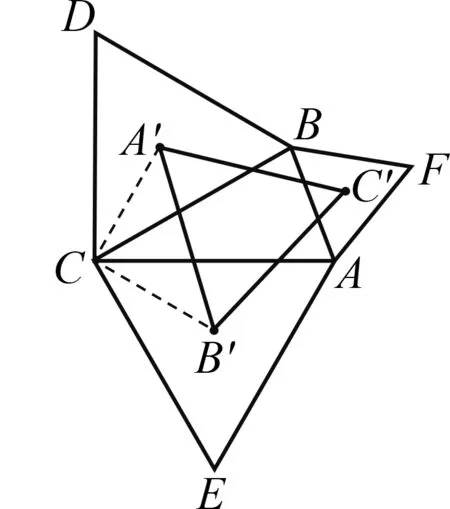
图1

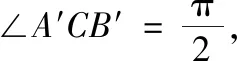
本题要求“以任意三角形的三条边为边，向外作三个等边三角形”，实际上，若向内作三个等边三角形，则这三个等边三角形的外接圆圆心仍然构成等边三角形，关于这一点，文[1]已给出相关的结论与证明．

·拿破仑定理

关于拿破仑定理的证明方法很多，这里不再赘述，下面给出拿破仑定理的符号语言形式及内外拿破仑三角形的定义．

结论1(拿破仑定理)任意△ABC以BC,AC,AB为边向外(向内)作三个等边三角形，其外接圆圆心依次记为A′,B′,C′(A″,B″,C″)，则△A′B′C′(△A″B″C″)为等边三角形，△A′B′C′(△A″B″C″)被称为外(内)拿破仑三角形．

证略．下文中的内外拿破仑三角形的顶点及其对应关系均参照上述结论1．

2 一般性结论

结论2已知△ABC的外接圆半径为r，外拿破仑三角形为△A′B′C′．若∠ACB=θ，记△A′B′C′的面积为S△A′B′C′，则

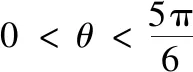
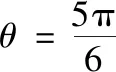
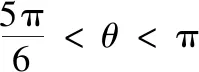
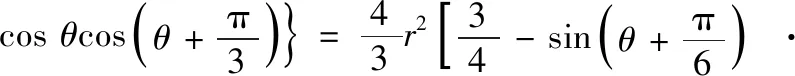
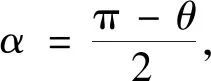
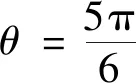
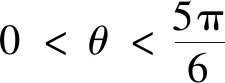
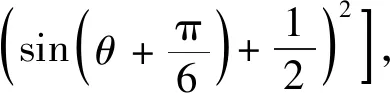
类似可得(3)，结论2得证．

类似于结论2，对于内拿破仑三角形有如下结论：

结论3已知△ABC的外接圆半径为r，△ABC的内拿破仑三角形为△A″B″C″．若∠ACB=θ，记△A″B″C″的面积为S△A″B″C″，则

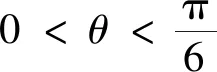
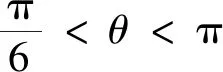
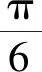
3 唯一性问题

以任意三角形的三条边向外(或向内)作正n边形，这3个正n边形的外心要构成等边三角形，n必须满足什么条件呢？

结论4任意△ABC以BC,AC,AB为边向外(向内)作三个正n边形(n≥3)，其外接圆圆心依次记为A′,B′,C′，若△A′B′C′为等边三角形，则n=3．

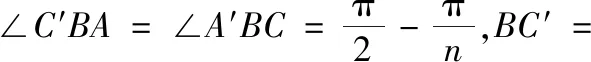
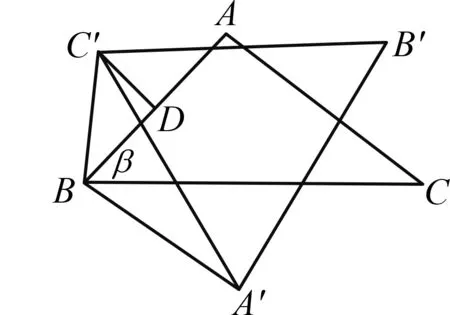
图2

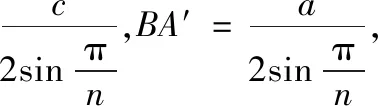
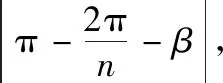
4 内外拿破仑三角形的位置关系

结论5若△ABC中最大角为∠ACB=θ，△ABC对应的外拿破仑三角形为△A′B′C′，内拿破仑三角形为△A″B″C″，则

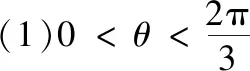
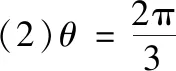
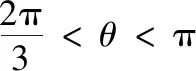
在证明该结论之前，我们先来看一个引理：

引理任意三角形的内外拿破仑三角形具有相同的外心．

该引理在文[1]中已经给出了详细的证明，故这里不再赘述．下面我们证明结论5．

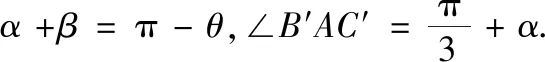
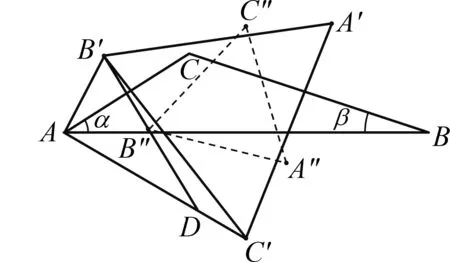
图3

下面先证(3)：

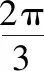
同理可证得A″在△A′B′C′外部，A″与B′在A′C′两侧，故由对称性得△A″B″C″三个顶点均在△A′B′C′外部，且B″与A′在B′C′两侧，C″与C′在A′B′两侧，A″与B′在A′C′两侧．

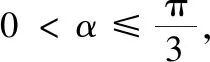
下证(2)：

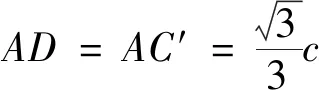
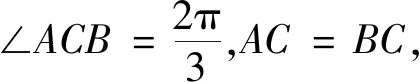
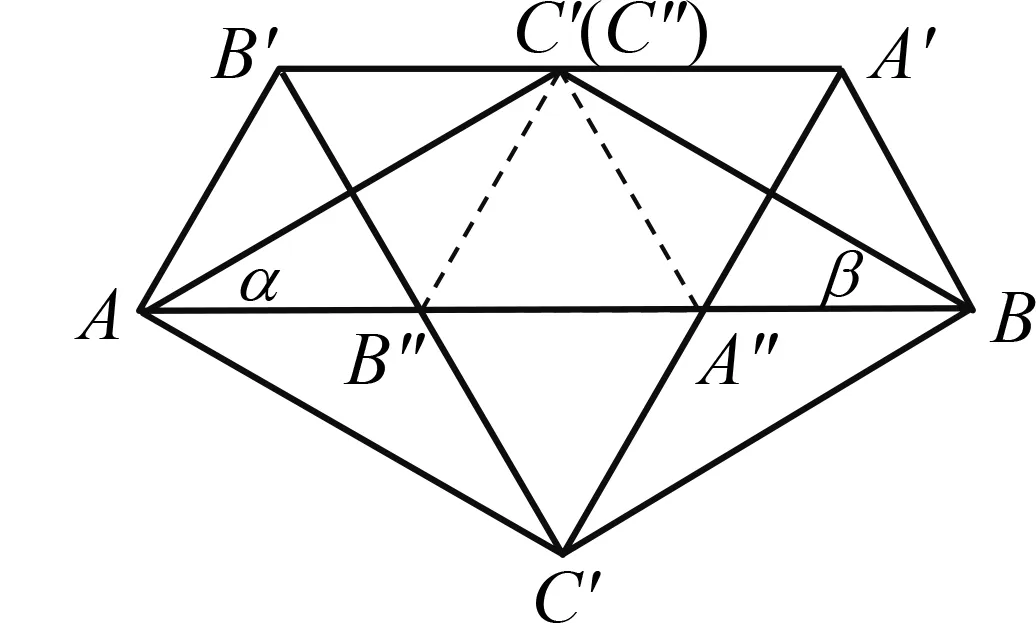
图4

分析 结合结论5以及内外拿破仑三角形的定义不难证出该推论，故这里不再赘述，相关证明读者可自行完成．