基于形心法的叶尖到达时刻高精度提取方法研究*
周 聪段发阶刘志博李 健
(天津大学精密仪器与光电子工程学院,天津 300072)
动叶片是航空发动机、燃气轮机、汽轮机等大型旋转机械核心做功部件,实时监测高速旋转叶片的振动参数,可以及时预警维修,保障设备的长期健康运行[1-3]。叶尖定时(Blade Tip Time,BTT)是监测旋转叶片振动的一种重要手段,在1965年Holz获得其专利[2],历经数十年的发展改良,目前被英国ROTADATA、法国FOGALE、德国MTU、美国HOOD、中国SMARTMENS等公司广泛应用于大型旋转机械的健康监测系统中,并实现了产品批量化定制生产,另外国内天津大学、西安交通大学、哈尔滨工业大学等高校研究所也对此有相应的研究[4-5]。
传统叶尖到达时刻(Time Of Arrival,TOA)提取方法采用模拟域的比较器获取TOA脉冲,并利用时间数字转换器(Time to Digital Converter,TDC)或现场可编程逻辑门阵列(Field Programmable Gate Array,FPGA)采集解析等方案进行TOA的计时传输等处理[6-8]。传统方案未能充分利用信号的整体信息,对信噪比(Signal to Noise Ratio,SNR)要求较高,易受噪声与信号强度波动等影响,时刻鉴别精度较差,但其具备工程实现简单与成本较低的优势。针对目前应用的光纤式叶尖定时传感器,传统方案可在高信噪比条件下达到较高的时刻鉴别精度,满足叶片振动测量的需求,已经实现产品化应用[8-9]。
针对传统方案的缺陷,郭浩天[10]提出基于软硬件优化的方案,此方案可减少叶尖间隙变化对TOA精度的影响,软件方案使用TOA脉冲信号的上升沿与下降沿确认叶片到达时刻,并对非对称叶片进行校准,硬件方案使用自动增益电路(Automatic Gain Control,AGC)稳定信号幅值;该方案可减少叶尖间隙变化的影响,但未能解决低SNR条件下的TOA获取。张继旺[11]提出了集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)用于TOA的提取,实验表明其叶片振动幅值与频率的测量误差分别小于2.89%和0.17%;但该方法难以实现板级处理,不具备工业应用条件。Qu等人[12]提出通过在叶片尖端增加微结构来减少叶尖间隙变化对TOA提取精度的影响,提高测量精度;该方案需要对叶片尖端增加微结构,工程应用有待进一步验证。
本文针对现有TOA提取方法的不足,提出基于形心法的叶尖到达时刻高精度提取方法。基于MATLAB平台从形心算法参数、ADC技术指标、滑动均值滤波器参数这三个维度探究其对时刻鉴别精度的影响,确定软件硬件电路的设计规格参数。基于FPGA平台实现形心的实时计算,进行板级实验对比验证,结果表明形心时刻鉴别精度大幅显著优于传统方案,具备较强的工程应用意义。
1 叶尖定时测振系统
叶尖定时传感器安装在机匣上,在定子上安装转速同步传感器,如图1所示。叶尖扫过叶尖定时传感器时的信号经过测量电路处理后,产生脉冲信号,记录叶片相对转速同步传感器的到达时间。由于叶片振动,叶片的到来时刻表现为超前或滞后,通过叶片振动提取算法对该时间序列进行处理,可获得叶片的振动信息。设转速为nr,叶端到转轴中心距离为r,假设叶尖到达时刻差值为Δt,则叶尖线速度v,以及振动位移x可表示为:


图1 传感器安装示意图
上式表明叶片的到达时刻差值会影响到叶片振动位移的测量,进而影响叶片振动参数的辨识。
目前叶尖定时测量主要有光纤式、电容式、微波式、电涡流式等,应用于不同的测量场景[12-15]。本文以耐高温、结构简单、不易受烟尘影响的电容传感器为例进行后续的软件仿真及实验。电容式叶尖定时传感器输出为类高斯信号[13],转子转速越高,信号的边沿会越陡峭,其带宽越宽,信号模型g(t)为:

式中:ε0为真空绝对介电常数,εr为工质的介电常数,d为叶尖间隙,k为转换系数,Ks为叶尖与传感器探头端面的最大重叠面积,σg为尺度参数,r为传感器芯极半径,δ为叶片厚度,v为叶尖线速度。实际测量的叶尖电容信号s(t)受环境因素和调理电路的影响,SNR较低,干扰源包括调制载波和随机白噪声,使用采集卡采集的叶尖电容信号如图2所示。
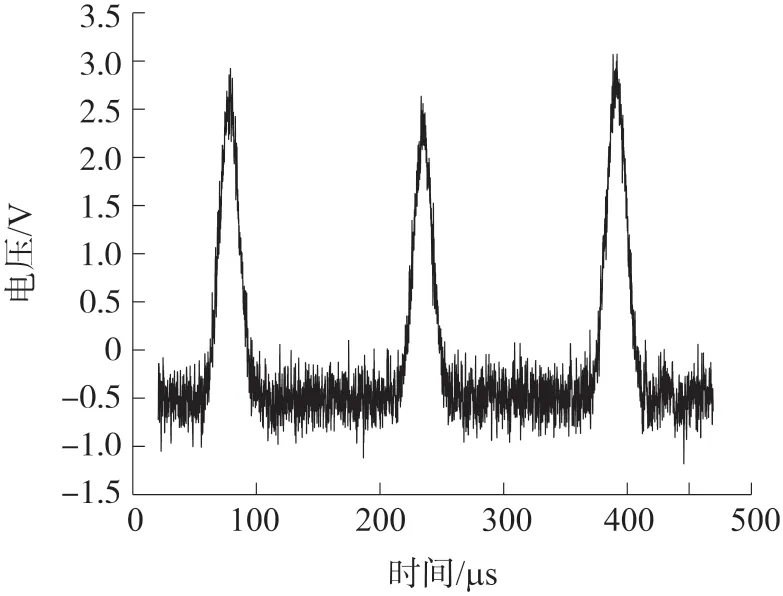
图2 电容式叶尖定时传感器输出信号
叶尖电容信号s(t)可通过高斯脉冲信号g(t)叠加高斯白噪声wgn(t)近似模拟。

针对此信噪比较低的信号,传统的时刻鉴别方案未能充分利用信号的整体信息,仅依靠信号的边沿获取叶尖到达时刻,会产生较大的误差,不满足叶片振动测量误差10 μm的需求,因此有必要设计一种抗噪强、对信号强度变化不敏感的TOA提取方法。
2 形心时刻鉴别原理及模型
形心是对象A中点集的平均,也被称为重心。针对本文研究的叶尖定时传感器输出的二维空间的模拟脉冲信号序列,其脉冲信号形心tc为:
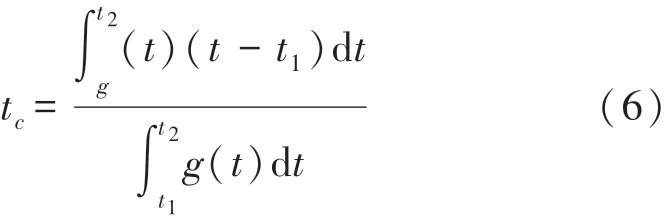
式中:t1与t2控制形心计算的窗口宽度wc。以脉冲信号形心时刻tc表征叶尖到达时刻tb,形心计算示意如图3所示。
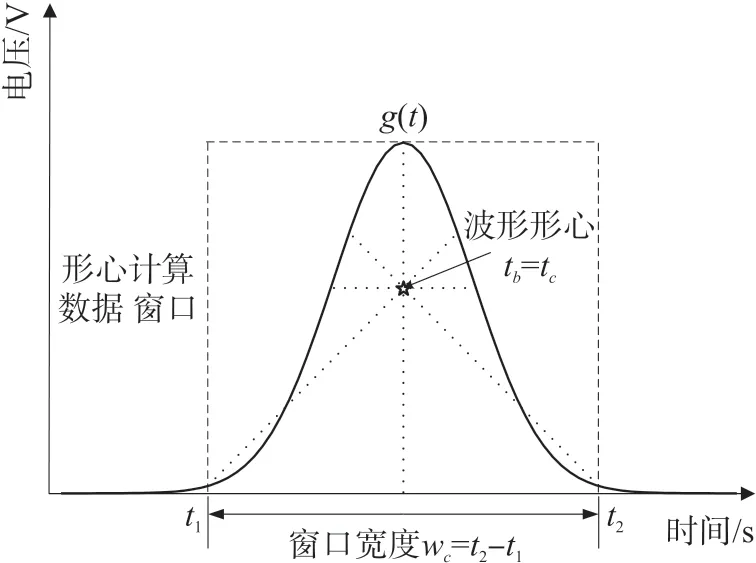
图3 形心计算示意图
以t0为间隔对s(t)进行采样量化,得到数字化的脉冲序列信号s(nt0)为:

依据式(6)与式(7),则叶尖到达时刻tb为:
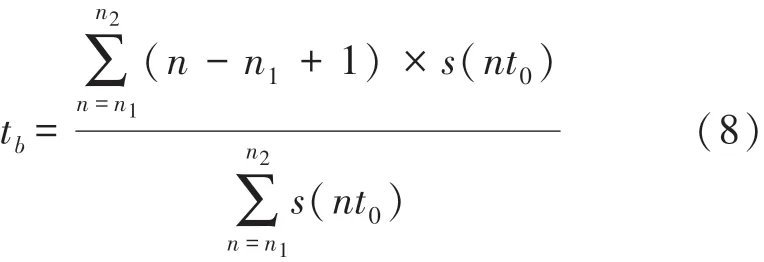
设幅值不同的脉冲序列信号s1(nt0)、s2(nt0)分别为:
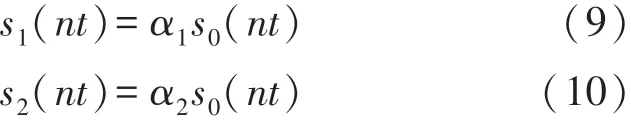
式中:α1与α2均为幅值常数,由式(8)~式(10)可得叶尖到达时刻tb1与tb2均为:

由式(11)易得,形心法从原理上消除了信号强度变化所引入的叶尖TOA提取误差。
现利用数学模型分析噪声对形心法提取叶尖TOA精度的影响,依据式(7)与式(8)可得:

式中:tgb为高斯信号的形心,tnb为高斯白噪声的形心。由高斯白噪声的随机性易得:

由式(12)~式(15)可得叶尖TOA鉴别误差Δtb为

由式(16)可知,TOA鉴别误差Δtb与白噪声的强度成正比,与信号的强度成反比。分子部分的白噪声在形心计算窗口wc内叠加削弱,分母部分的越大,Δtb越小。为了提高TOA精度,需使n1~n2部分尽可能包含有效信号数据点,即增大形心计算的窗口宽度wc。
通过提高信号的强度来改进形心计算方案,即利用信号的指数运算结果来计算其形心,改进的叶片到达时刻为:
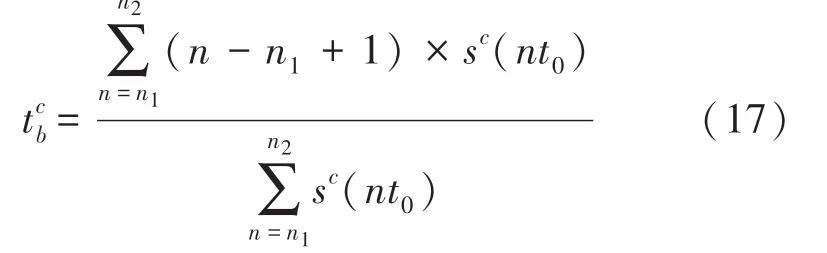
本小节通过对提出的形心时刻鉴别算法的数学模型分析发现,该算法不受信号强度影响,抗噪性能强,仅需要基本的算术运算即可完成形心的计算,可以实现板级数据的实时处理,有利于实现工程应用。
3 仿真实验及结果分析
3.1 参数设置
为保证形心时刻鉴别算法在获取最优的叶尖TOA基础上,算法逻辑实现的面积与速度均衡,依据电容式叶尖定时传感器输出信号模型与形心时刻鉴别模型,设置的仿真参数见表1:
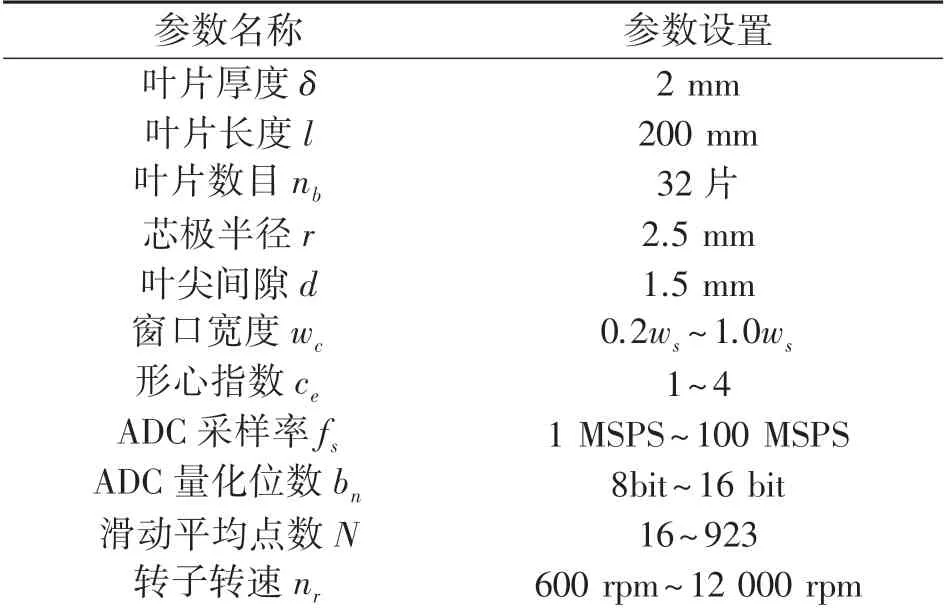
表1 形心时刻鉴别法仿真参数
表1设置了叶片厚度、叶片长度、叶片数目、探头半径这些与信号模型相关的平台参数;制定了形心算法参数、ADC技术指标与滑动均值滤波器参数范围,以研究这三个维度参数对形心时刻鉴别精度的影响。
为比对不同转速下的叶尖TOA误差Δtb,将Δtb转化为叶片振动位移测量误差Δxb,依据式(1)与式(2)可得:
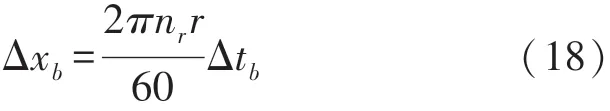
3.2 形心时刻鉴别算法参数确定
形心时刻鉴别算法中的窗口宽度wc与形心指数ce这两个参数影响形心时刻鉴别精度。定义ws为电容式叶尖定时传感器输出信号的脉冲宽度,σs为信号模型的尺度参数:

利用MATLAB搭建仿真测试平台,在平台参数基础上,设置形心算法参数的窗口宽度wc在区间0.2ws~1.0ws内、形心指数ce在区间1~4内;ADC技术指标中的采样率fs为50 MSPS、量化位数bn为12 bit;滑动均值滤波器中的平滑点数N为128;转速nr为12 000 rpm,依据式(3),生成SNR为20.0 dB的脉冲信号,并对此信号序列仿真10 000次,统计并绘制时刻鉴别标准差随窗口宽度的变化曲线,如图4所示。

图4 时刻鉴别标准差随窗口宽度的变化曲线
由图4可知,形心指数ce为2、3、4时,时刻鉴别标准差σb随窗口宽度wc的增加而单调递减,在0.2ws~1.0ws区间内趋于平缓,当ce为2时,算法最优,其中σb为18 ns;ce为1时,在0.2ws~0.7ws区间内,σb随wc的增加而单调递减,在0.7ws~1.0ws区间内,σb随wc的增加而单调递增,当wc为0.7ws时,σb最优为20 ns。在ce均处于最优窗宽的情况下,ce为2的时刻,鉴别标准差σb相对ce为1、3、4时分别减少了6.7%、8.1%、18.0%。因此在后续的仿真以及逻辑实现中设置形心指数ce为2,窗口宽度wc在区间0.8ws~1.0ws内。
3.3 ADC技术指标确定
形心时刻鉴别基于全波形处理方案,需要使用模拟信号离散量化后的数字信号,实时计算其波形形心。ADC可使模拟域的脉冲信号序列离散量化为数字域的脉冲信号序列,为时刻鉴别模块提供实时的数据流。ADC在模数转换的过程中有许多关键的技术指标,其中采样率fs与量化位数b是影响时刻鉴别精度的重要指标。
利用MATLAB搭建仿真测试平台,在平台参数基础上,设置wc为0.8ws、ce为2、fs在区间1 MSPS~100 MSPS内、bn在区间8 bit~16 bit内、N为128;nr为12 000 rpm,依据式(3),生成SNR为15.0 dB的脉冲信号,并对此信号序列仿真10 000次,分别统计并绘制峰值时刻鉴别、前沿时刻鉴别与形心时刻鉴别算法的标准差随ADC采样率与量化位数的变化规律,如图5所示:
分析图5仿真结果可得:

图5 时刻鉴别标准差随ADC技术指标的变化规律
①由(a)可知,当量化位数bn为12 bit,采样率fs从1 MSPS至100 MSPS时,峰值时刻鉴别标准差σpb从最高529 ns单调递减至224 ns,在50 MSPS~100 MSPS区间内,变化趋于平缓。当fs为50 MSPS,bn从8 bit至16 bit时,σpb从330 ns单调递减至220 ns,12 bit~16 bit区间内,变化趋于平缓。
②由(b)可知,当量化位数bn为12 bit,采样率fs从1 MSPS至100 MSPS时,前沿时刻鉴别标准差σeb从329 ns单调递减至104 ns,在20 MSPS~100 MSPS区间内,变化均趋于平缓。当fs为20 MSPS,bn从8 bit至16 bit时,σeb无明显变化,在8 bit为最优值110 ns。
③由(c)可知,当量化位数bn为12 bit,采样率fs从1 MSPS至100 MSPS时,形心时刻鉴别标准差σcb从91 ns单调递减至28 ns,在20 MSPS~100 MSPS区间内,变化趋于平缓。fs为20 MSPS,bn从8 bit至16 bit时,σcb无明显变化,在12 bit为最优值28 ns。
④随着ADC采样率的提高,峰值时刻鉴别、前沿时刻鉴别、形心时刻鉴别三类算法精度均有一定程度的提升;当峰值时刻鉴别采样率达到50 MSPS,采样率的提升对算法精度的提升无明显优化,与仿真信号的SNR相关;当前沿时刻鉴别与形心时刻鉴别采样率达到20 MSPS,采样率的提升对算法精度的提升无明显优化;峰值时刻鉴别相对前沿时刻鉴别与形心时刻鉴别需要较高的采样率。
⑤随着ADC量化位数的提高,峰值时刻鉴别的精度略有提升,前沿时刻鉴别与形心时刻鉴别精度无明显优化。
⑥在最优条件下,形心时刻鉴别标准差28 ns为峰值时刻鉴别标准差220 ns的12.7%,为前沿时刻鉴别标准差110 ns的25.5%;从统计分析的结果可知,基于全波形分析的形心时刻鉴别的精度相对传统时刻鉴别方案有大幅提升,符合理论分析的结论。
综上可知,针对带宽为250 kHz的电容式叶尖定时传感器,形心时刻鉴别需要ADC采样率至少为20 MSPS,量化位数至少为10 bit。在SNR=15 dB的情况下,形心时刻鉴别标准差为28 ns,据此可知叶片振动位移测量标准差为7.0 μm,满足叶片振动测量误差10 μm的设计指标。
3.4 滑动均值滤波器参数确定
拟在数字处理系统中加入滑动均值滤波器。固定点数的滑动均值滤波器仅适用于转速变化范围较窄的信号降噪,但本文所研制的模块应用转速范围为600 rpm~12 000 rpm,因此有必要探究滑动均值滤波器点数N与转子转速nr对形心时刻鉴别精度的影响,为滑动均值滤波器的数字逻辑设计提供理论支撑。
滑动均值滤波器结构简单,易于实现,适用于平滑波形中的毛刺,是一种经典的数字低通滤波器,其截止频率fc的计算公式如下:

利用MATLAB搭建仿真测试平台,在平台参数基础上,设置wc为0.8ws、ce为2、fs为40 MSPS、bn为10 bit、N在区间16~923内;nr在区间600 rpm~12 000 rpm内,依据式(3),生成SNR为20.0 dB的脉冲信号,并对此信号序列仿真10 000次,分别统计并绘制形心时刻鉴别算法的叶片时刻鉴别标准差与叶片振动测量标准差随转速与平滑点数的变化规律,如图6及图7所示。
分析图6、及图7仿真结果可得:
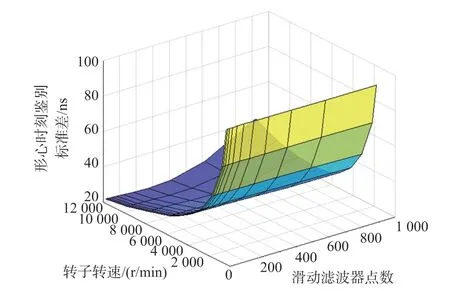
图6 形心时刻鉴别标准差随转速与平滑点数的变化规律

图7 叶片振动测量标准差随转速与平滑点数的变化规律
①当平滑点数N为273,转速nr从600 rpm增至12 000 rpm时,形心时刻鉴别标准差σcb由最高95 ns单调递减至20 ns。
②当平滑点数N为273,转速nr从600 rpm增至12 000 rpm时,叶片振动测量标准差σva由最低1.2 μm单调递增至5.0 μm。
③随着转速的提升,形心时刻鉴别精度逐渐提升,但叶片振动测量精度逐步降低。随着平滑点数的增加,形心时刻鉴别精度与叶片振动测量精度在固定转速下,均表现为先提升至拐点再逐步降低。
④分析恒定转速下的最优平滑点数可知,当nr为12 000 rpm时,N=273的5.0 μm为N=923的10.4 μm的48.1%;当nr为8 000 rpm时,N=410的4.2 μm为N=923的5.3 μm的79.2%;当nr为6 000 rpm,N=615的3.6 μm为N=923的3.91 μm的92.1%。由此可知随着转速的增加,最优N在逐渐增加。
⑤分析统计图的整体变化规律可知,增大平滑点数N对形心时刻鉴别精度无明显提升。
综上可得,转速在600 rpm~12 000 rpm范围内,为使逻辑资源消耗与时刻鉴别精度达到均衡,预设滑动滤波器点数N为273用于后续的仿真与数字逻辑实现。
3.5 小结
本节确立形心算法、ADC技术指标、滑动均值滤波器这三个维度参数影响形心时刻鉴别精度。利用MATLAB软件平台仿真,确定了形心算法参数中的窗口宽度wc为0.8ws,形心指数ce为2;ADC技术指标中的采样率fs为40 MSPS,量化位数bn为10 bit;滑动均值滤波器的平滑点数N为273;基于全波形分析的形心时刻鉴别的精度相对传统时刻鉴别方案有大幅提升。
4 板级实验验证
使用RIGOL的DG2052任意波形发生器作为输入信号源,输出叠加白噪声的高斯脉冲,模拟电容式传感器输出的脉冲序列,进行板级实验,对比形心、传统的峰值与前沿时刻鉴别的精度。DG2052输出波形抖动在200 ps以内,可作为定时基准用于本文设计的分辨力为10 ns的时刻鉴别模块。
本平台使用ADC+FPGA+ARM组合方案进行验证平台的设计,使用FPGA驱动多通道高速ADC实现数据的实时处理,并使用ARM与FPGA的AXI接口进行算法参数的配置以及叶尖到达时刻数据的传输,最后利用PC客户端通过千兆以太网访问运行在ARM上的Jupyter服务器以进行数据的实时分析对比,如图8、9所示。
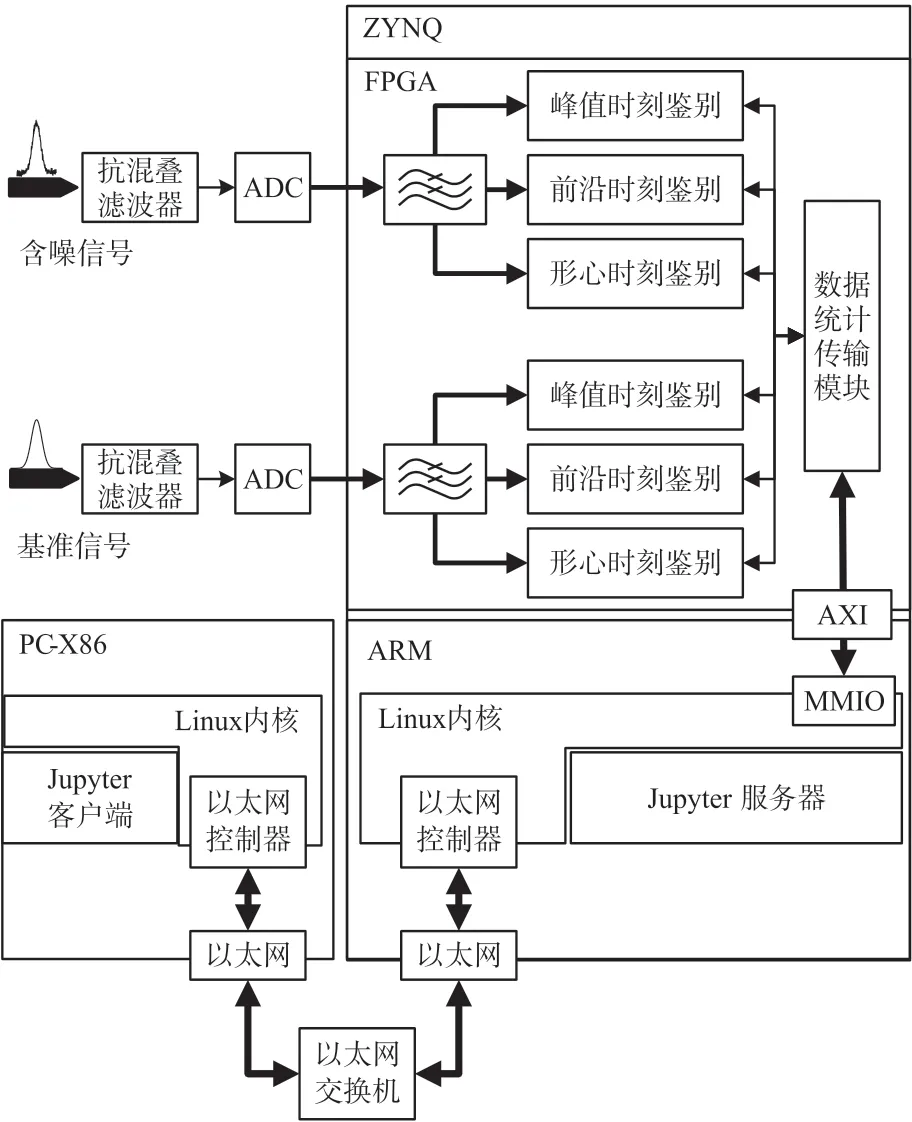
图8 软硬件设计框图
使DG2052输出320 Hz至6 400 Hz噪声叠加比例为30%的高斯脉冲信号,仿真叶片数目nb为32,转速nr在600 rpm~12 000rpm区间的转台,分析10 000条脉冲信号的峰值时刻鉴别、前沿时刻鉴别与形心时刻鉴别标准差σb,其随转速nr的变化曲线如图10所示。

图10 时刻鉴别标准差随转速的变化曲线

图9 平台实物图
由图10可知,转速在600 rpm~12 000 rpm区间内,形心时刻鉴别精度均优于峰值时刻鉴别与前沿时刻鉴别,随着转速的增加,时刻鉴别精度在逐渐提升;形心时刻鉴别在转速为600 rpm时的标准差为87 ns,仅为峰值时刻鉴别标准差1631 ns的5.3%,前沿时刻鉴别标准差1 156 ns的7.5%;在转速为12 000 rpm时的标准差为19 ns,为峰值时刻鉴别标准差113 ns的16.8%,前沿时刻鉴别标准差73 ns的26.0%。
固定转速为12 000 rpm,白噪声比例从0%增至50%,分析10 000条脉冲信号的三种时刻鉴别标准差σb,其随白噪声强度的变化曲线如图11所示。
由图11可知,叠加比例在0%~50%区间内,形心时刻鉴别精度均优于峰值时刻鉴别与前沿时刻鉴别,并且噪声比例为0%时的σb为5 ns,为峰值时刻鉴别9 ns的55.6%,前沿时刻鉴别5 ns的100.0%;噪声比例为50%时的σb为45 ns,为峰值时刻鉴别230 ns的19.6%,前沿时刻鉴别172 ns的26.2%。

图11 时刻鉴别标准差随噪声叠加比例的变化曲线
对比实验数据表明,噪声叠加比例在20%~50%区间内形心时刻鉴别的标准差远小于传统的峰值时刻鉴别与前沿时刻鉴别的标准差,因此该方法具备较强的抗噪性能,可以有效的实现叶尖到达时刻的提取。
5 结束语
本文针对传统叶片达到时刻提取方法存在的缺陷,提出了基于形心法的叶尖到达时刻高精度提取方法。通过分析形心时刻鉴别原理及模型提出使用信号的指数运算结果来计算其形心、优化时刻鉴别精度;确立形心算法、ADC技术指标、滑动均值滤波器这三个维度参数影响形心时刻鉴别精度,判定其具备对信号强度不敏感、抗噪性能强与易于数字逻辑实现等特性。通过仿真确定了形心算法实现所需的技术参数,为硬件实现形心算法提供理论依据。板级实验表明形心时刻鉴别具备较强的抗噪性能,精度大幅优于传统的方法,有效地实现叶片到达时刻的提取。

