Stewart六维力传感器寿命特性的诊断与优化*

李德伦高 波张 运谢宗武张 兵

(1.哈尔滨工业大学 机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001；2.空间智能机器人系统技术与应用北京市重点实验室，北京空间飞行器总体设计部，北京 100094；3.陕西电器研究所，陕西 西安 710065)

六维力传感器作为空间机械臂“触觉”感知系统的核心部件，可实时监测机械臂的环境载荷，为机械臂的力控制和运动控制提供必要的力感知信息，对机械臂实现智能化、柔顺化起到至关重要的作用[1-2]，同时能够辅助机械臂的舱段转位，为悬停飞行器捕获及对接、舱外货物搬运、航天员出舱、舱外检修、设备维护等空间任务的实现提供保障[3-4]。不同于地面机械臂，空间机械臂具有在轨维修难、使用寿命长等特性，而传感器位于空间机械臂臂体与末端执行器的连接位置，更换及维修难度大，故传感器除应满足产品的功能/性能要求外，还应具备高可靠性的使用寿命。因此，对传感器寿命特性开展研究具有重要的研究意义。目前，针对于六维力传感器的设计分析及优化改进，国内外学者已有一定的研究，Uchiyama等提出了六维力传感器各向同性评价系数，并分析了传感器对称设计与评价系数的影响关系。张景柱等[5]分析了Stewart六维力传感器结构尺寸与灵敏度性能指标之间的量化关系，提出一种传感器结构参数设计的简便方法。姚建涛等[6]系统研究了Stewart六维力传感器各向同性性能指标，阐明了各向同性度性能指标之间存在一定的制约关系，并以解析表达式的形式给出了综合性能指标最优时结构参数之间的关系。贾振元等[7]通过分析力及力矩一阶静力影响系数矩阵和力及力矩柔度矩阵，揭示了传感器的各向同性、灵敏度及结构参数之间的相互关系，并用图谱优化和遗传算法，求解Stewart六维力传感器最佳性能指标结构参数。王航等[8]依据传感器任务模型，以解析表达式的形式给出了基于任务的评价传感器结构性能优劣的数学描述。但关于空间机械臂Stewart六维力传感器寿命特性的工程化研究相对较少。

笔者针对空间机械臂Stewart六维力传感器(简称传感器)使用寿命低的问题，结合传感器结构参数分析理论、疲劳寿命理论，对传感器低寿命问题开展诊断分析与试验研究，验证传感器寿命特性理论优化方法的有效性。

1 Stewart六维力传感器参数设计与性能评价

经典Stewart六维力传感器参数模型如图1所示，整体结构由6个支路弹性杆件与上、下平台铰接而成。在原理上各支路弹性杆件只承受沿轴心线方向的拉/压力(不考虑重力和摩擦力的影响)，通过检测与转换各支路弹性杆件的组合变形，实现对空间载荷的测量。决定传感器综合性能的5个结构参数[9-10]为RA、RB、aA、aB及H，其中RA、RB为上、下平台球铰点的分布半径；H为上下平台的几何中心距离；aA、aB为上、下平台定位角。

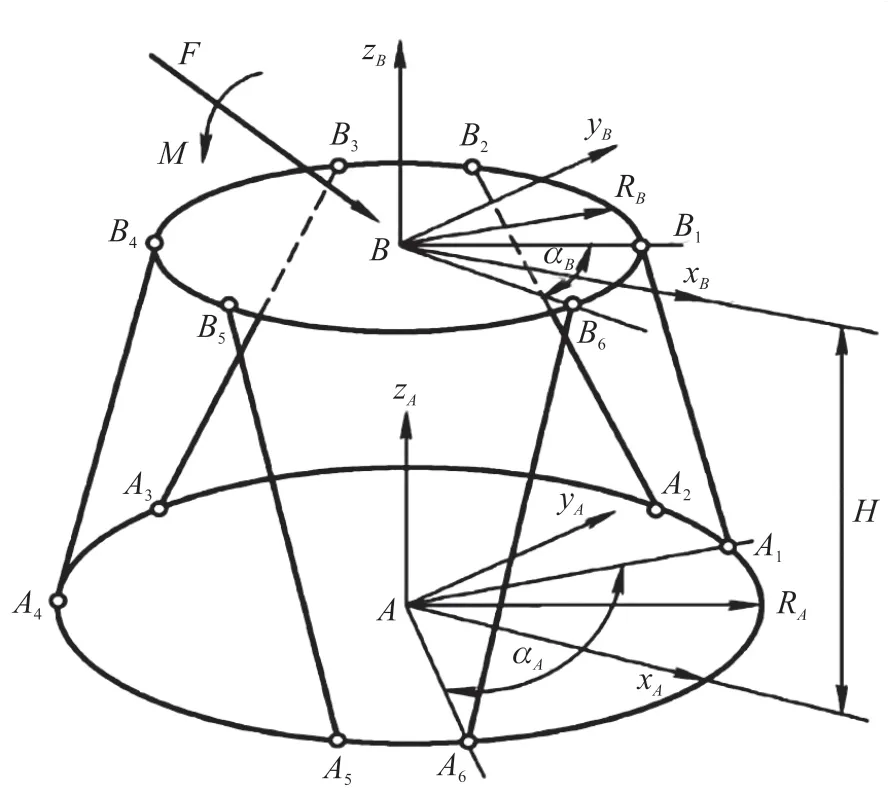
图1 Stewart六维力传感器参数化模型

根据Stewart并联机构平台的力螺旋理论和虚功原理[11-12]，存在广义力平衡方程

式中:fi为第i个弹性杆件的轴向力；φ为第i个弹性杆件轴线相对基准坐标系的单位线矢；FF、FM分别为施加于上平台作用力的主矢和对坐标原点B的主矩。

式(1)亦可表示为

式中:f＝[f1，f2，f3，f4，f5，f6]T为6个弹性杆件轴向力矢量；F＝[FF，FM]T为承载平台所受的外力矢量；G为(一阶静力影响系数矩阵)一阶正向映射影响系数矩阵。

式中:C为(力雅克比矩阵)一阶逆向映射影响系数矩阵。

传感器结构性能与构成正/逆向映射影响系数矩阵G/C的结构参数有关，由力/力矩各向同性度、力/力矩灵敏度各向同性度来描述[13]，表达式为

式中:uF，uM，ηF，ηM分别称为力各向同性度、力矩各向同性度、力灵敏度各向同性度和力矩灵敏度各向同性度。λ为矩阵的特征值，cond为矩阵的条件数。

4个指标数值越接近1，表示传感器各向同性度性能越好，抗外界影响能力越优，然存在传感器各同性度相互制约，4个指标不能同时满足最优[14-15]。

2 寿命特性分析及评价

现有的理论研究中，未见有关于Stewart六维力传感器传感器寿命特性的分析。因此，为提升该类传感器的综合性能及任务适应能力，对Stewart六维力传感器的寿命特性开展研究。

本文优化对象的测量方式为应变电阻式测量，为便于分析，作出如下假设:①传感器的6个支路弹性杆件特性一致；②所有零部件满足经典材料力学的基本假设。由材料力学理论，支路弹性杆件的轴向力与应力σ关系为

联立式(1)～式(5)可得

式中:A为支路弹性杆件等效横截面积。

依据实际工况，传感器主要受复杂工作载荷与环境温度载荷影响，二者综合影响可由各支路弹性杆件产生的应力大小进行描述。因此，传感器寿命特性可依据名义应力疲劳理论开展分析，由恒幅应力水平与疲劳寿命循环次数进行评价。针对宇航产品小样本量的特点，寿命模型采用3参数S-N疲劳曲线函数，该模型能够更好地描述传感器的寿命特性，表达式为

式中:S，N为材料所受的交变应力幅和对应的疲劳循环次数；Q为理论疲劳极限；β，P为S-N曲线形状参数。

依据等寿命曲线，等寿命应力与实际平均应力(R≠-1)间的转换关系为

式中:σj为等寿命曲线中单级最大应力幅值；σm为应力均值；σs为材料屈服强度；j为载荷谱级数。

依据MINER线性累积损伤理论，传感器各级应力谱恒幅应力下的中值疲劳寿命表达式为

由假设可知，传感器自身为线性测量系统。分析中将所有影响因素所产生的应力作叠加等效，对载荷谱作归一简化，即取n＝1。联立式(6)～式(10)，得广义力矢量与寿命特性矢量关系式为

令

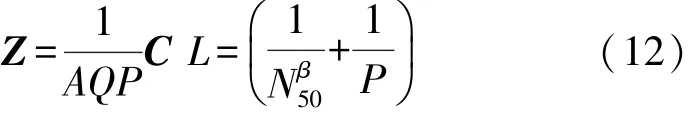
式(11)可表示为

式(13)表达了传感器寿命特性的优劣取决于力/力矩影响系数矩阵Z，并可由结构参数表示。当广义外力的模为无量纲单位1时，对应矢量模的极值为传感器寿命特性的表征指标。寿命特性矢量L模的极值可表示为

当外力矢量F，M的模分别为单位1时，满足以下关系

依据拉格朗日极值法构造函数

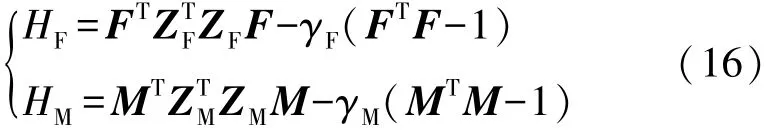
式中:γF、γM为力/力矩拉格朗日乘子。

联立求解，得LF，LM的极值为矩阵的最小特征值λ的平方根。则传感器的寿命特性指标表达式为

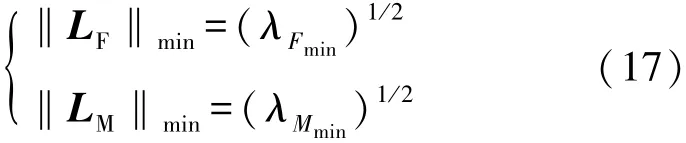
式(17)为传感器寿命特性优劣的评价依据，当‖LF‖，‖LM‖越小时，传感器的寿命特性越好。

3 寿命优化

3.1 参数优化

工程设计中，往往需根据不同的任务需求，开展以多项性能指标为目的的综合优化分析，针对空间高维传感器，以力/力矩各向同性度、灵敏度各向同性度及疲劳寿命为优化目标，定义目标函数表达式为

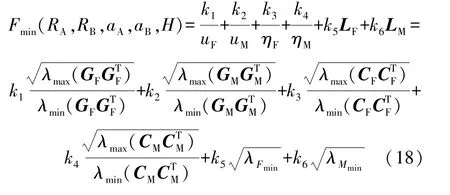
式中:k1～6为各性能指标的权重系数，由于技术指标中力量程与力矩量程的不匹配性，力矩使用量程为0～800 N·m，力的使用量程为0～2 000 N，而上下平台半径分别为100 mm和150 mm，经对未优化的Stewart六维力传感器进行有限元仿真计算，单维加载及多维复合加载时满量程状态下力矩产生的最大应力值为力产生的最大应力值的1.5倍～3.6倍、最大应力区平均值的2.1倍～3.2倍，结合特制国军标钛合金TC4疲劳性能曲线图谱(由西北有色金属研究院提供)，材料在力满载时的疲劳寿命为在力矩满载时的疲劳寿命的5倍左右，故设置力矩寿命性能指标权重系数为力寿命性能指标权重系数的5倍，出于均衡性考虑，最终设置权重为K＝[1，1，1，1，1，5]。

兼顾计算高效性，将决定传感器综合性能的3个结构参数规化如下:

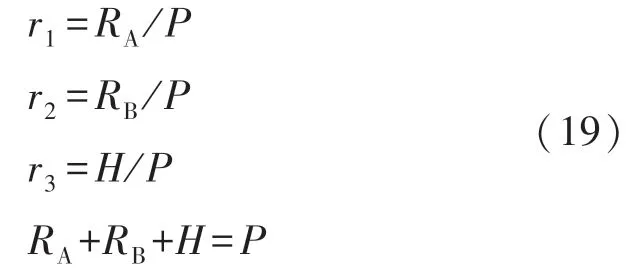
式中:由于外包络限制，参数P的取值范围为P∈(0，936)mm。

综合技术指标要求，目标函数表达式(18)中的参数满足如下条件，

采用遗传算法作为目标函数的优化工具，其流程如图2所示。值得注意的是遗传算法具有一定的随机性，顾需反复运行程序得到最优结果，表1给出了优化前后后的传感器结构参数，表2为优化前后模型的性能指标。

图2 基于遗传算法的传感器结构参数优化流程图

表1 两版模型的结构参数

表2 两版模型的各项性能指标对比

由表2可知，优化后传感器力各向同性度上升了20.7%，而力矩的各向同性度下降了11.5%；力灵敏度各向同性度下降了15.2%，而力矩灵敏度各向同性度上升了27.9%；力疲劳寿命性能下降了23.9%，而力矩疲劳寿命性能提高了44.0%。由上述分析可知，经目标参数优化，传感器综合性能可有效改善。

3.2 仿真计算

现采用SolidWorks静力分析和疲劳分析模块，对传感器力学性能及疲劳寿命进行仿真计算。参照理论分析，疲劳仿真时平均应力修正采取Soderberg-屈服强度准则，可靠性系数设为1.5。图3和图4是优化前后模型受载荷(额定工作载荷与温度载荷)时von Mises应力分布情况；图5和图6是基于上述应力仿真结果而得到疲劳寿命分布情况。

图4 优化模型应力分布

由图3～图6可知:①模型优化后，支路弹性体处的应力分布更加均匀，且最大应力值(弹性体应变梁处)小于未优化模型的25%。一般情况下，von Mises应力值越大的区域，在此区域材料越容易出现疲劳破坏产生裂纹，弹性体越容易发生破损，从而破坏失效。②传感器应力分布得到明显改善，其疲劳寿命(次数)较优化前提升了97%，仿真结果与理论分析趋势一致，说明该优化方法较好地实现了预期的设计目标。

图3 未优化模型应力分布

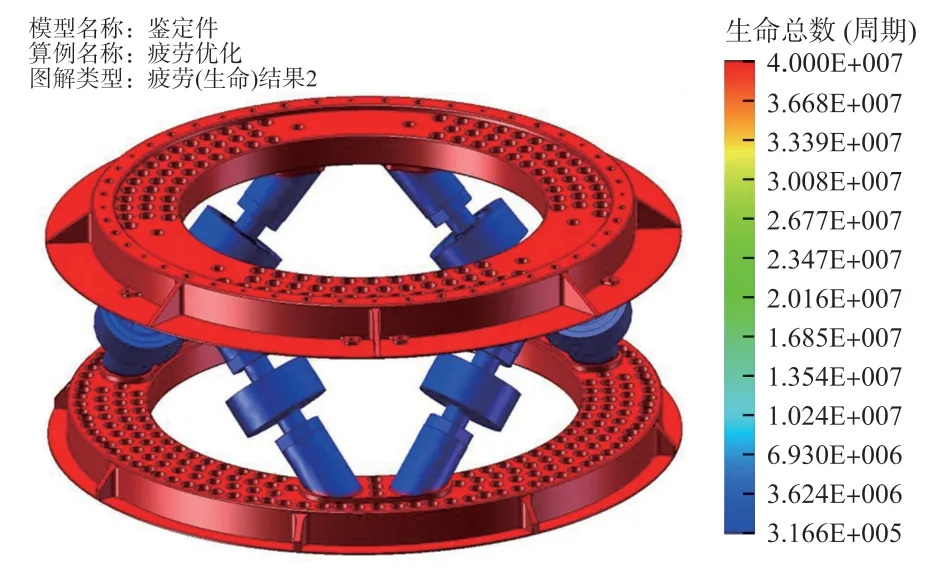
图6 优化模型寿命分布

4 实验验证

基于优化结构参数，研制一版Stewart六维力传感器样机(简称优化样机)，优化前/后样机如图7所示。二版样机除结构参数外所有特性(技术状态、生产基线)一致。为验证理论分析有效性，逐项开展了循环疲劳(R＝0)、薄膜转换元件完整性、疲劳后功能/性能及材料力学性能实验。

图7 实物样机

4.1 实验基础

弹性体材料的寿命S-N曲线参数及力学性能实验按照HB 5287-1996、GB/T 3075-2008要求，采用疲劳试验机及金属材料拉力试验机实现。样机整机疲劳、静标实验采用本单位自研设备多维标定系统实现，如图8所示。

图8 多维标定系统

4.2 疲劳实验

由空间机械臂工作模式分析可知，传感器在执行任务时主要受外部载荷作用下的结构应力以及恶劣工作环境引起的结构热应力影响，故疲劳加载的量程由以上两种应力综合等效而成。图9为疲劳实验过程中，各支路传感器的均值零点输出(基于自由无约束状态)变化趋势(基于力传感器的评价体系，传感器稳定性可由零点输出表征)。

图9 均值疲劳零点变化趋势

由图9可知:①二版样机的均值疲劳零点在前14万次具备相同的变化趋势，即在2 000次加载后达到装配稳定状态，各支路的零点增量满足任务精度要求(设计零点输出精度为优于0.3%；二版样机满输出分别约为15 mV/11.6 mV，7.5 V DC供电)；②在14～24万次的区间内，二版样机的均值疲劳零点呈递增趋势，差异比例变大；且在18万次时，未优化样机的均值疲劳零点输出精度不满足任务要求，且已出现零飘趋势。

4.3 薄膜转换元件验证实验

薄膜转换元件是传感器电信号输出的重要环节之一，评价薄膜稳定性的优劣主要取决于复合膜层中的绝缘膜层与合金膜层的性能。

溅射基体的弹性体结构为十字梁圆膜片构型，该结构中间是受力硬中心结构，应变梁为对称分布，溅射应变区位于梁的底面，应力凹槽的正下方。当受载时弹性体弯曲变形，属于正应力型传感器。薄膜应变片及弹性体结构如图10所示。

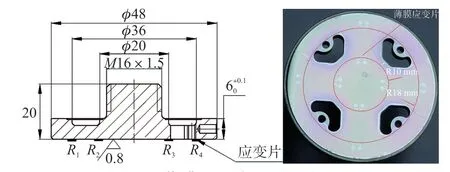
图10 薄膜应变片及弹性体结构

为排除薄膜转换元件的影响，对疲劳实验中均值零点输出变化大的未优化样机，进行支路传感器输出阻抗(表征合金膜性能)、电桥绝缘阻抗(表征绝缘膜性能)的测量，数据见表3。

表3 未优化样机薄膜转换元件特性参数

由表3可知:①未优化样机各支路薄膜转换元件，疲劳实验前后的表征特性一致；后续的样机零点输出(空载)测量无变化(数据未给出)。②表明未优化样机薄膜转换元件具备完整性。③疲劳实验中的异常零点输出存在如下情况:传感器受载后，材料内部可能出现局部的应力集中情况，导致应力积累损伤，出现故障模式。

4.4 传感器性能实验

为验证疲劳应力积累损伤对传感器综合性能的影响程度，继续对二版样机进行单维及复合加载，表4为单维弯矩Mx(表征传感器单维精度特性)加载实验性能数据。图11为传感器性能实验(加载实验与刚度实验)图，加载实验采用本单位自研设备多维标定系统进行，如图11(a)所示。刚度实验参照本单位研制的多维标定系统刚度标定标准执行，图11(b)为刚度标定示意图。

图11 传感器性能实验

由表4可知，未优化样机各支路弹性杆件的力学性能相对于优化样机明显降低，降低幅度约为3倍～16倍；同时各杆件产生的应变值与外载荷关系呈较大的非线性。表明弹性材料受到疲劳应力积累损伤，材料的屈强比、弹性滞后性变化明显，导致支路弹性杆件3项指标性能降低。

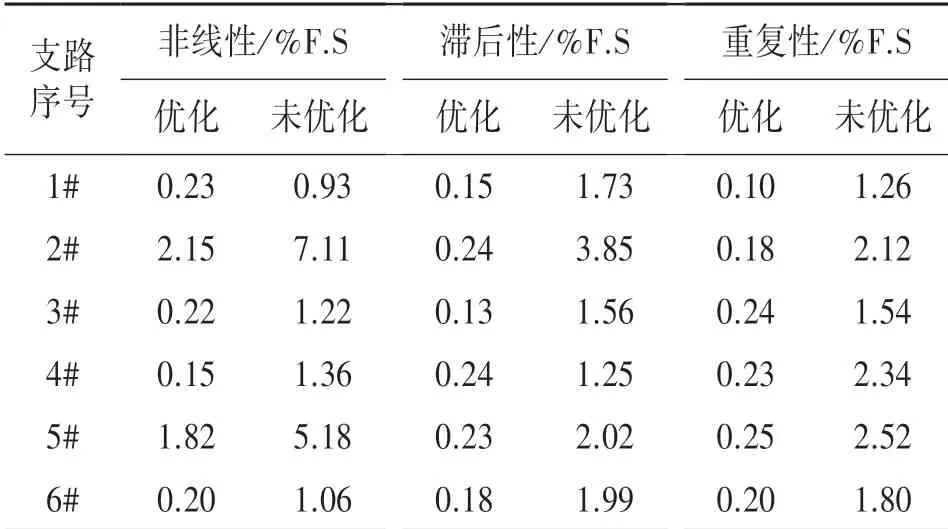
表4 在Mx弯矩作用下各支路弹性杆件性能参数

在此基础上开展单维标定与多维复合(由整臂工况分解)标定的加载实验，精度性能数据见表5、表6，刚度性能数据见表7。

表5 两版样机的单维性能 单位:%

表6 两版样机的多维精度

表7 两版样机的刚度特性

由表5～7可知，①在精度方面，未优化样机的单维、多维复合精度相对于优化样机明显降低，降幅约为1.3倍～14倍。在大量程加载时，维间耦合大，传感器系统已无法满足线性叠加特性，性能超出精度指标要求。②在刚度方面，未优化样机的各维刚度相对于优化样机明显降低，降幅约为18%～24%。表明传感器在受载过程中，弹性体应变区出现较大应力集中，材料内部可能有裂纹损伤情况，甚至伴有一定的塑形变形。

4.5 材料力学特性实验

进一步验证疲劳应力累积损伤对材料的力学特性的影响程度。按照GB/T 5193-2007要求，利用超声探伤仪，对二版样机的各支路弹性体(拆卸后)进行裂痕损伤情况的无损检测；再按照GB/T 5168-2008要求，利用高倍显微镜对二版样机的各支路弹性体进行内部高倍组织检测。图12为未优化样机高倍组织检测弹性体切面中裂纹情况。图13为优化样机高倍组织检测中弹性体切面情况。再进行各弹性体的力学特性检定(按表8顺序)，数据见表8、表9。

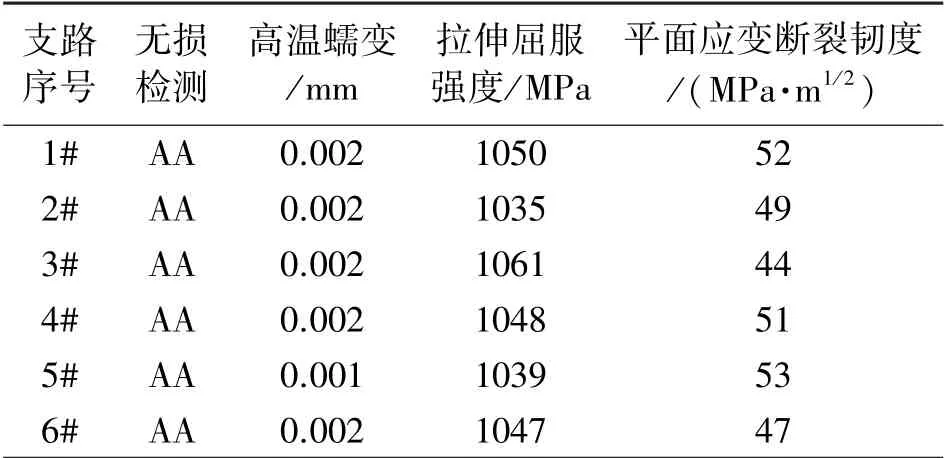
表9 优化样机各弹性体材料的力学特性

图12 未优化样机弹性体高倍组织

图13 优化样机弹性体高倍组织

表8 未优化样机各弹性体材料的力学特性

由图12、13及表8、9可知，①通过超声无损检测表明经过24万次疲劳加载实验后，未优化样机弹性体材料的内部结构存在损伤，单个不连续孔孔增大，且有裂纹。优化样机弹性体材料内部分区域内晶粒组织有微变形，但未产生结构损伤。②未优化样机各弹性体材料的力学特性相对于优化样机各向指标明显降低；(3)优化样机断裂韧度约为65 MPa·m1/2，其抵抗裂纹扩展的能力(疲劳主要由裂纹扩展的的速度和寿命决定)较强，即在材料应力较低且较均衡状态下，传感器疲劳寿命好。

6 结论

针对空间机械臂Stewart六维力传感器使用寿命低的问题开展了诊断分析、优化以及试验研究。提出了传感器寿命特性的评价体系与判定准则，建立了一种针对该类传感器的通用性结构参数优化方法。该方法可使传感器各支路弹性杆件的应力状态均衡化，使各支路弹性杆件达到低应力工作状态，可有效提升传感器寿命。通过理论分析、样机验证实验，证明了该优化方法的有效性。本文研究内容也为Stewart六维力传感器的性能分析与结构优化提供了有益的指导。