基于改进MPC算法的汽车稳定性控制研究
谷 磊
(徽商职业学院商贸系,安徽 合肥 231201)
科技的进步促进了汽车的多元化发展,燃油汽车、新能源汽车等不同种类的汽车大大拓宽了用户的选择范围。但不管什么种类的汽车,如何确保其稳定性控制性能都是一个永恒的话题。目前,电子稳定程序(electronic stability program,ESP)是最普及的汽车稳定性控制系统,该控制系统具有操作简单、控制性能良好的特点。除市场上的控制系统外,在学术方面学者也进行了大量研究,如秦程现等[1]以ESP控制系统为基础,结合模糊控制算法与四通道液压制动模型,以汽车横摆角速度为控制变量,实现了对汽车的稳定性控制。结果表明,该控制系统可确保汽车行驶过程中的安全性,提高对汽车稳定性的控制能力。在此基础上,李少志等[2]为进一步提高汽车在极限工况下的稳定性控制性能,提出一种包含紧急侧倾控制的综合控制策略,避免了汽车在极限大转向工况下容易侧翻的问题,提高了汽车的抗侧翻能力;李绍松等[3]设计了一种基于ESP的PID控制器,通过合理分配控制器子系统权重,实现车辆稳定性控制。相较于其他控制系统,该控制器可提高汽车对参考轨迹的跟踪性能。ESP控制系统虽然具有一定优势,但其在对参考轨迹进行跟踪时,仍存在一定的跟踪误差。为解决该问题,更好地实现对汽车稳定性控制,本文以当下在控制领域具有高控制精度的模型预测控制(model predictive control,MPC)算法为基础,通过采用并行混沌算法(parallel chaos algorithm,PCOA)优化其目标函数,提出一种基于改进MPC算法的汽车稳定性控制策略。
1 动力学模型构建
本文以分布式电驱动汽车为研究对象,建立如图1所示的八自由度汽车整车模型。
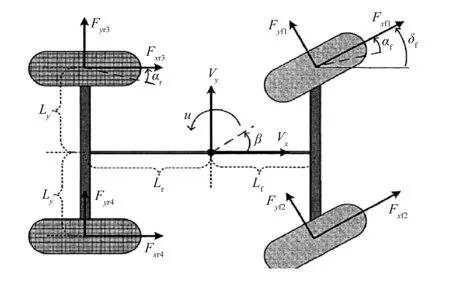
图1 汽车动力学模型
根据动力学方程,X轴方向的动力学方程为[4]:
maz=∑Fx=Fxfcosδf+Fxr
(1)
式中:m为车辆质量;a2为汽车纵向加速度;Fx为车轮所受纵向力;Fxf=Fxf1+Fxf2,为两前轮所受纵向力;Fxr=Fxr1+Fxr2,为两后轮所受纵向力;δf=δf1+δf2,为两前轮转向角。
Y轴方向的动力学方程为[5]:
may=∑Fy=Fyr+Fyfcosδf+Fxfsinδf
(2)
式中:Fy为车轮所受横向力;ay为汽车横向加速度;Fyr=Fyr1+Fyr2,为两后轮所受纵向力。
横摆运动动力学方程为[6]:
I2η=∑M=LfFxfsinδf+LfFyfcosδf-LrFyr+ΔM2
(3)
式中:I2,M为整车绕质心转动惯量和转矩;η为整车横摆角速度;Lf,Lr分别为前两轮几何中点和后两轮几何中点到质心距离;ΔM2为汽车直接横摆转矩[7]。
考虑到汽车的横摆稳定性主要受质心侧偏角、横摆角速度、滑移率影响[8],可通过控制汽车电机分配转矩和输入前轮转向角进行控制。同时为避免汽车失控,对以上变量进行条件约束。
根据经验公式,将质心侧偏角β的临界值取值范围设为:
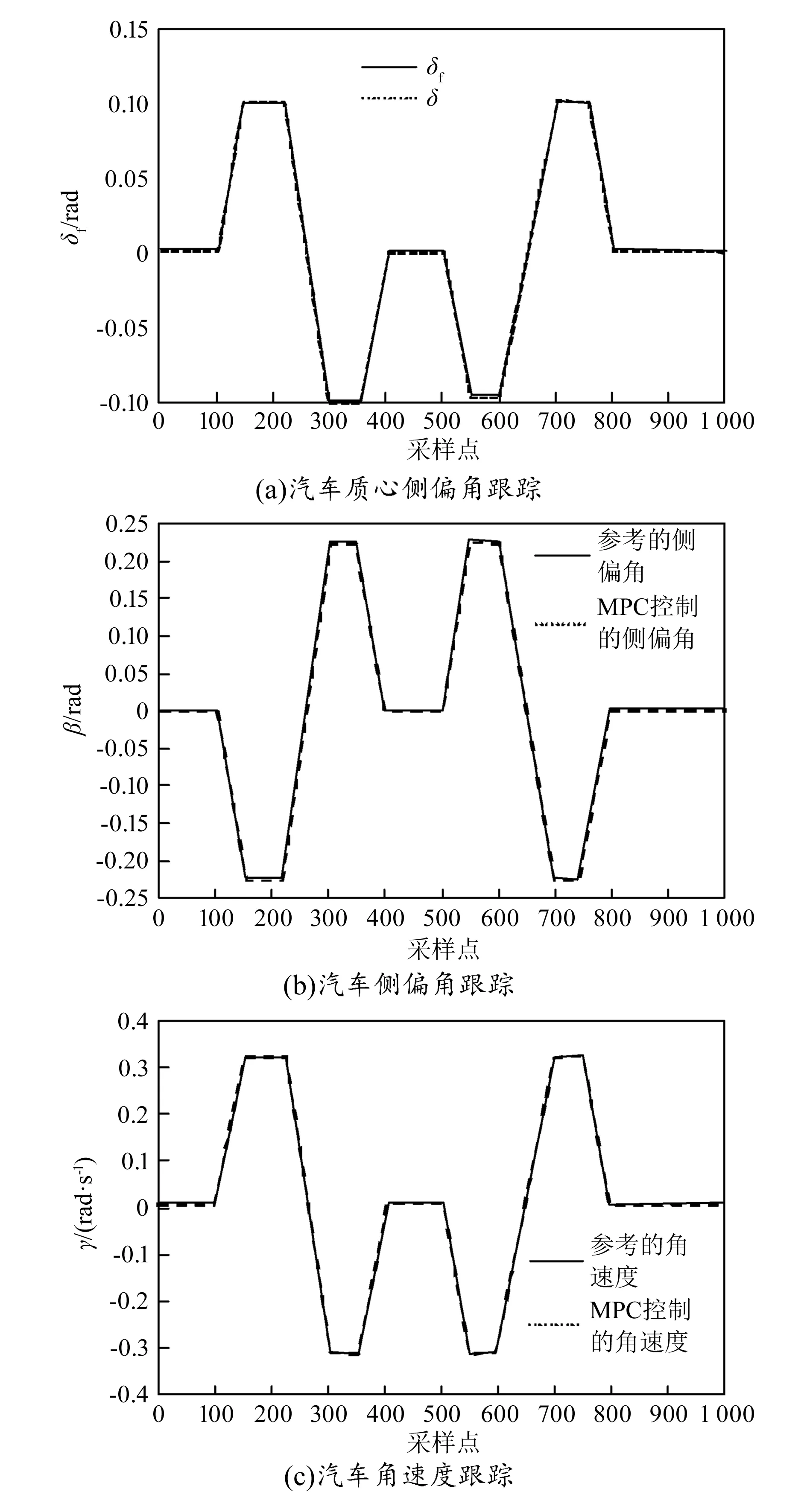
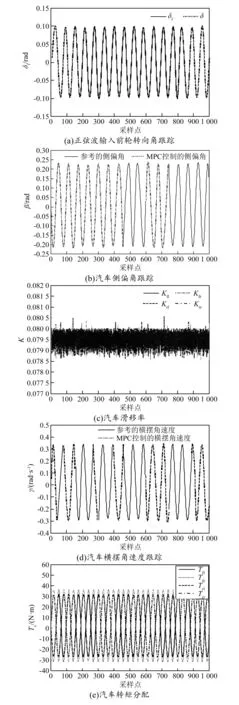
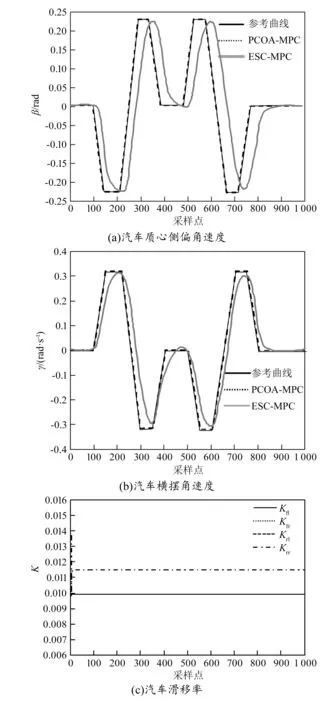
-arctan(0.02μg)<β (4) 横摆角速度η的临界值取值范围为: (5) 式中:μ为路面附着系数;g为重力加速度;vx为整车质心纵向的速度。 滑移率K的临界值取值范围为: -10% (6) 为减少整车能量损耗和保持车辆运行的稳定性,设定转矩Tc的取值范围为: Tc≤185 N·m (7) MPC算法是一种基于模型的闭环优化控制方法,包含模型预测、滚动优化和反馈校正3个部分,其控制原理如图2所示[9]。其中,模型预测负责使系统输出值无限接近期望值;滚动优化则包括滚动和优化两部分含义,滚动即采用滚动方式降低算法误差,优化即求解最优解并输出[10];反馈校正负责将误差反馈给系统,从而保证闭环系统的稳定性[11]。 图2 MPC算法控制原理 MPC控制为离散控制,因此本文采用差分方程作为预测模型。假设采样点k为: (8) 式中:t为总运行时间;Ts为固定步长。则预测模型为: x(k+i|k)=fk[x(k+i-1|k),u(k+ i-1|k)]Ts+x(k+i-1|k) (9) 式中:fk为状态随时间变化梯度;x(k+i-1|k)为状态量;u(k+i-1|k)为系统将来的输入变量;i为相当于当前采样点所预测的(k+i)时刻。由此可得到每个状态量的差分方程: x1(k+1|k)={[Fyf(x1(k),x2(k),u1(k))+Fyr(x1(k),x2(k))]/(mvx)-x2(k)}Ts+x1(k) (10) x2(k+1|k)={[LfFyf(x1(k),x2(k),u1(k))-Lr+Fyr(x1(k),x2(k))+ΔM]/I2-x2(k)}Ts+x2(k) (11) (12) (13) (14) (15) 式中:xq(k+1|k)为状态量xq在(k+1)时刻的状态量,q=1,2,3,4,5,6;xq(k)为xq在k时刻的状态量;uq(k)为xq(k)对应的将来输入变量;ΔM为整车直接横摆转矩;R为车轮半径;J为车轮的转动惯量;Ckq为第q个状态量对应的输出变量值。 定义控制域为Z,预测域为P,则模型预测输出为: y(k+i|k)=Cx(k+i|k)=Cfk[x(k+i-1|k),u(k+i-1|k)]Ts+x(k+i-1|k) i∈[1,P],C∈[-1,1] (16) 式中:Cx(k+i|k)为输出变量值;C为输出变量值的取值区间。 根据汽车稳定性控制特点,建立目标函数。 构建质心转向角β和横摆角速度η误差最小的目标函数S1。 (17) 式中:Y(k)为实际的质心转向角的值;R(k)为横摆角速度的值;Q=diag(Q1,Q2),为权重矩阵,其中Q1,Q2分别为质心侧偏角和横摆角速度的误差在目标函数中的权重系数;β(k+i|k)为质心转向角在预测的(k+1)时刻的值;βr(k)为质心转向角在当前采样点k的值;η(k+i|k)为横摆角速度在预测的(k+1)时刻的值;ηr(k)为横摆角速度在当前采样点k的值。 构建使驱动力矩最小的目标函数S2: (18) 式中:U(k)为未来的控制输入序列;Tcf1为左前轮的驱动力矩;Tcfr为右前轮的驱动力矩;Tcr1为左后轮的驱动力矩;Tcrr为右后轮的驱动力矩;R1和R2分别为车轮转向角和四轮控制转矩所占的权重因子,设定权重矩阵R=diag(R1,R2,R2,R2)。 为保证驾驶的舒适性,应保证控制动作尽可能小或为零,由此有: (19) 式中:A1和A2分别为车路转向角和四轮控制转矩变化率,并设定权重矩阵A=diag(A1,A2,A2,A2)。 根据上述的目标函数,构建总的目标函数Smpc: (20) 式中:ΔU(k)为控制动作的变化率。 本文采用PCOA[12-13]对目标函数进行滚动优化求解,具体步骤如下: (21) 4)根据映射公式(22)将迭代后的混沌变量映射到优化变量遍历区间。 (22) 式中:[cij,dij]为第i个优化变量对应的第j个并行混沌变量值xij的定义域。 5)计算每组输出量对应的参考状态变量输出值[14],并选择目标函数更大的值作为最佳目标函数值。 6)若算法满足终止条件,则结束算法,反之则返回步骤5)。 在MATLAB软件上构建动力学模型,同时结合以上构建的MPC控制器。忽略摩擦力、空气阻力、俯仰运动、整车荷载等,将汽车实车参数设置如下[15]:整车质量m=1 359.8 kg,轮胎直径d=0.58 m,车轮转动惯量J=0.35 kg·m2,转矩最大值Tmax=185 N·m,整车质心高度h=0.512 m,质心转动惯量I2=1 992.54 kg·m2,质心到前轮距离Lf=1.063 m,质心到后轮距离Lr=1.485 m,两轮距离Ly=0.431 m。 实验中将模型参数设置如下:模型运行时间t=10 s,固定步长Ts=0.005 s,权重矩阵Q=diag(10 000,1 800),R=diag(10,10,10,10),A=diag(200,200,200,200),预测域P=6,控制域Z=6,并行混沌优化迭代步长T=5 000。 3.3.1控制效果验证 为验证改进MPC控制器的有效性,通过改变输入前轮转向角形式和车速,观察模型跟踪汽车质心的侧偏角速度、横摆角速度、车轮转矩,从而分析改进MPC控制器对汽车稳定性的控制效果。 1)不同输入前轮转向角形式。 图3所示为车速60 km/h时本文所提方法对汽车稳定性的控制结果,其中图3(a)中的δf表示两前轮转向角,δ表示主动转向角。图3(d)中的Kf1,Kfr,Kr1,Krr分别表示前左右轮、后左右轮的纵向滑移率,图3(e)中Tf1,Tfr,Tr1,Trr表示前左右、后左右4个轮毂电机的转矩分配。由图3可知,使用本文所提方法对汽车进行控制后,质心侧偏角轨迹、横摆角速度、汽车轮胎滑移率的跟踪误差分别小于0.006 rad、0.018 5 rad/s、8%,满足汽车稳定性控制要求,且当汽车以较小偏角转向时,本文所提方法可对汽车4个轮毂电机转矩进行合理分配,同侧轮毂电机转矩相同,满足转弯需求。 图3 车速60 km/h时的仿真结果 2)不同车速。 设定汽车初始速度为50 km/h,固定输入为稳定性正弦波,改变汽车运行速度,得到所提方法控制下汽车的稳定性,如图4所示。由图可知,本文所提方法对汽车横摆率、侧偏角的跟踪误差较小,与参考轨迹几乎重合;对汽车轮胎滑移率控制在0.081之内,满足汽车轮胎稳定性和转弯转矩要求。由此说明,本文所提方法可有效跟踪汽车参考轨迹,实现对汽车稳定运行的控制。 图4 初速50 km/h时的仿真结果 3.3.2控制效果对比 为进一步验证本文所提方法的有效性,实验分别采用PCOA求解目标函数和基于极值搜索控制(extreme value search control,ESC)求解目标函数,并对比两种求解方法的控制效果,结果如图5所示。由图可知,ESC-MPC对汽车质心侧偏角速度、横摆角速度和车轮滑移率的变化趋势可进行准确跟踪,但与参考轨迹存在一定误差;本文所提的PCOA-MPC方法可良好跟踪汽车质心侧偏角速度、横摆角速度和车轮滑移率参考轨迹,几乎与参考轨迹重合,跟踪误差更小。整体来看,相较于ESC-MPC方法,PCOA-MPC方法的控制效果更好,对参考轨迹跟踪误差更小。 图5 不同控制方法下汽车稳定性仿真结果 综上所述,本文所提的改进MPC算法,可提高控制系统的跟踪性能。相较于ESC对比控制方法,本文所提方法的MPC轨迹控制与汽车运行参考轨迹拟合度更高,跟踪误差更小,可实现对分布式驱动电动汽车稳定性的良好控制,为汽车稳定性控制研究提供了理论参考。但由于实验条件限制,本文仅在MATLAB软件上对算法进行仿真验证,未进行实车实验。下一步,在条件允许的情况下,应考虑本文所提算法的实际应用性能,以增强其实用性。2 基于改进MPC算法的汽车稳定控制器设计
2.1 MPC算法简介
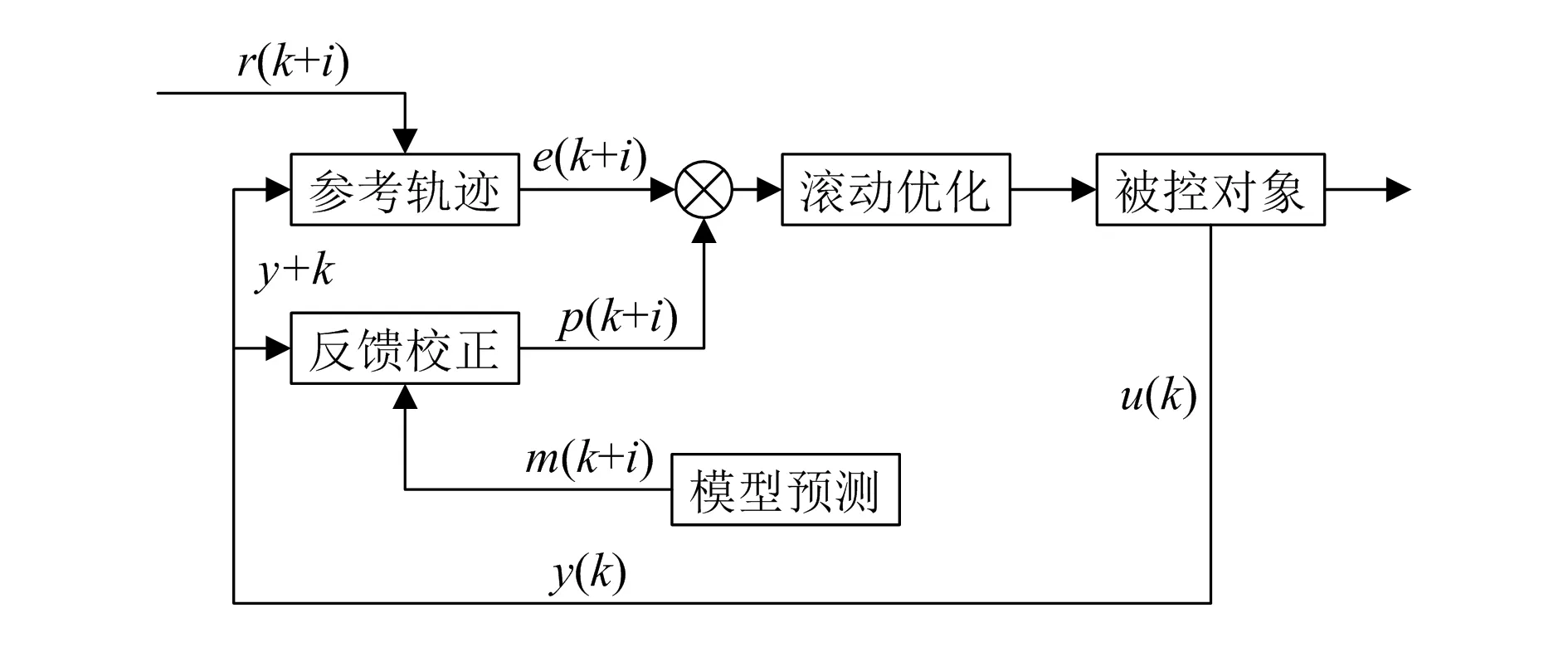
2.2 MPC预测模型构建
2.3 目标函数设定及求解
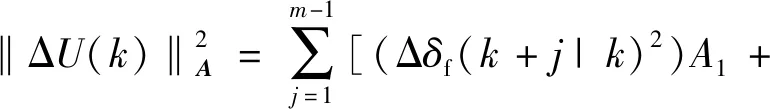
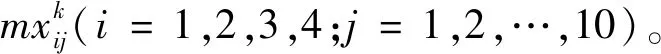
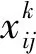
3 仿真实验
3.1 实验环境
3.2 模型参数设置
3.3 结果与分析
4 结束语

