绳驱动机械臂运动控制方法研究

彭嘉伟，廖万能，王尧尧,2，丁亚东，吴洪涛

(1.南京航空航天大学机电学院，江苏 南京 210016)(2.浙江大学流体动力与机电系统国家重点实验室，浙江 杭州 310027)

随着旋翼飞行器的发展，人们越来越不满足于其仅拥有拍照、摄像等简单功能。为了增加旋翼飞行器空中作业的主动性，研究者们在飞行器上加装了机械臂[1-2]。然而现阶段的机械臂大多是传统的工业机械臂，其刚性大、质量大、能耗高、结构复杂，对旋翼飞行器机身稳定有很大干扰[3-4]。文献[5]、[6]研究发现，绳驱动机械臂结构简单且质量轻，将关节驱动器安装于基座使得机械臂对机身的干扰变小，能较好地匹配旋翼飞行器，但绳驱动技术使得机械臂的相邻关节存在耦合问题，同时绳索的柔性使得机械臂的刚度降低。此外，由于绳驱动机械臂系统模型复杂，以及存在参数不确定性和外部干扰，使得该系统的精确动力学模型几乎无法获得。

为了简化绳驱动机械臂系统模型，采用时延估计 (time delay estimation，TDE)[7]获得系统模型的估计状态。TDE通过采样将过去很短一段时间的系统状态作为下一时刻系统的模态输入。对比其他控制方法，TDE可以有效减少系统动力学模型中的参数，从而得到简单有效的控制器。文献[8]针对可变载荷下平面机械臂的连续跟踪控制问题，基于TDE提出关节运动控制器，取得了良好控制效果。

由于滑模变结构控制对系统具有较好的鲁棒性，很多学者已将其用于非线性系统控制研究[9]，但他们大多运用了线性滑模(linear sliding mode，LSM)变结构控制。为了加快系统在平衡点附近的收敛，将幂指数引入趋近律公式，终端滑模(terminal sliding mode，TSM)变结构控制应运而生[10]。然而因为幂指数存在，控制信号输入可能出现奇点，为解决这一问题，学者们提出了非奇异终端滑模 (nonsingular terminal sliding mode，NTSM)[11]控制器，将所需控制量降到了合理范围。

本文基于TDE控制框架，引入非奇异终端滑模关节运动控制器，以保证绳驱动机械臂系统在复杂干扰下有良好的控制性能。为更好地控制输出与输入的关系，改善控制器在滑模面附近的趋近律，加入了模糊控制策略，以减少干扰和参数变化对机械臂控制效果的影响。

1 绳驱动机械臂结构设计

绳驱动机械臂设计时参考了课题组先前设计制作的水下绳驱动机械臂[12],并由Zhao等[13]负责画图、制作。为了满足旋翼飞行器的空中作业要求，对机械臂做了一些轻量化处理，机械臂板采用尼龙材料，其热变形温度为145 ℃，抗拉强度为48 MPa,弯曲强度为43.5 MPa。关节轴采用铝合金材料。因为电机驱动关节是通过绳索传递力矩的，所以对每个关节设计了张紧装置。将驱动电机安装在基座上，以减小机械臂运动时带来的惯性力矩。为了测得各个关节运动过程中的位置信息，在各关节轴的一端处设计安装有关节编码器。上述设计基本满足机械臂本身轻量化、对飞行器基座扰动小、降低能耗的要求。绳驱动机械臂的三维图如图1所示，参数见表1。

表1 绳驱动机械臂参数表

2 绳驱动机械臂动力学模型

绳驱动机械臂动力学模型的代数形式为：

(1)

(2)

(3)

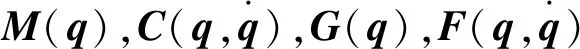
综合式(1)、(3)可以得到：

(4)

(5)

(6)

式中：H为绳驱动机械臂所有未建模动力学与所有外部未知干扰之和，其值用时延估计技术获得。

3 非奇异终端滑模控制器设计

3.1 控制器设计

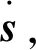
(7)

(8)

式中：α=diag([α1α2…αn]),k1=diag([k11k12…k1n]),k2=diag([k21k22…k2n]),ρ=diag([ρ1ρ2…ρn]),γ=diag([γ1γ2…γn])；e为绳驱动机械臂系统关节轨迹跟踪误差，e=qd-q，其中qd为关节的期望轨迹，该轨迹连续有界且存在二阶导，所以有：

(9)

sig是一个自定义函数，满足sig(a)b=|a|bsgn(a)，a，b∈R。sgn是一个符号函数，满足

(10)

根据式(5)、(7)、(8)，可以将绳驱动机械臂的控制器设计为：

(11)

(12)

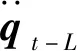
(13)

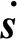
(14)

由式(5)和式(14)可以推导出系统误差动力学模型

(15)

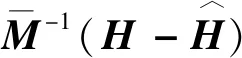
(16)

(17)

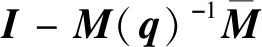
3.2 控制器稳定性证明

引理1 如果a1,a2,a3,…,an都是正值，则下列不等式成立：

(18)

引理2 如果李雅普诺夫函数V(x)满足以下条件：

(19)

那么V(x)可以在有限的时间内从V(x0)到V(0)，时间T满足：

(20)

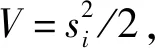
kc2isig(si)γi)-αiρiεi]

(21)

式(21)可以写成以下两种形式：

(22)

(23)

将式(22)改写为：

(24)

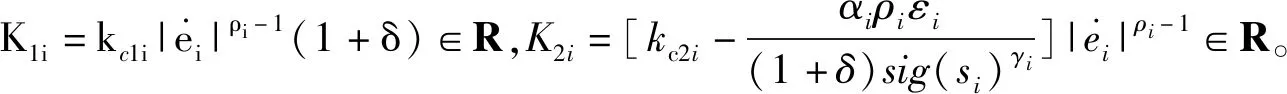
从引理1，可以推出：

(25)

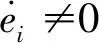
(26)

(27)

同理，对于式(23)可以得到：

(28)

(29)

综上所述，只要存在一个估计误差εi，那么si就可以收敛到某个滑模面区域，该区域可以表示为：

|si|≤Δ=min{Δ1,Δ2}

(30)

(31)

至此，控制器的稳定性证明完毕。

3.3 控制系统搭建

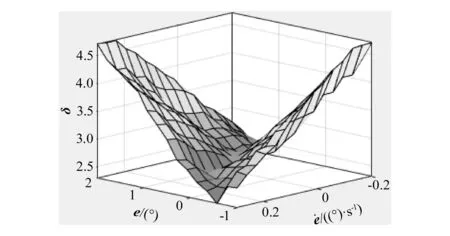
图2 模糊控制器的控制面

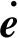
综上，针对绳驱动机械臂的运动控制问题，基于时延估计的模糊非奇异终端滑模控制器(NTSN+Fuzzy)设计方案如图3所示。

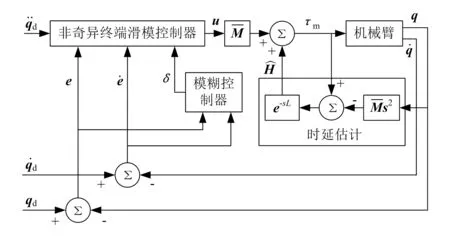
图3 基于时延估计的终端滑模控制

4 仿真实验与数据分析

为了验证模糊非奇异终端滑模控制器设计的有效性，在一定实验周期内，将本文设计的控制器与非奇异终端滑模控制器、线型滑模控制器进行控制效果对比。

非奇异终端滑模控制器(NTSM)如下：

(32)

线型滑模控制器(LSM)如下：

(33)

表2 工况1下关节1和关节2控制误差的Rms值和Max值 单位：(°)

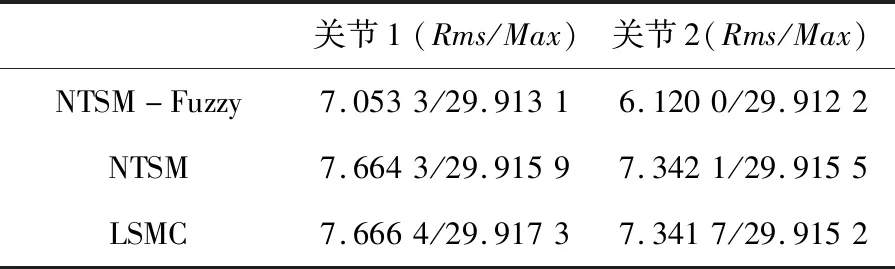
表3 工况2下关节1和关节2控制误差的Rms值和Max值 单位：(°)

图4 工况1关节跟踪轨迹

图5 工况1关节跟踪误差

图6 工况1关节跟踪力矩

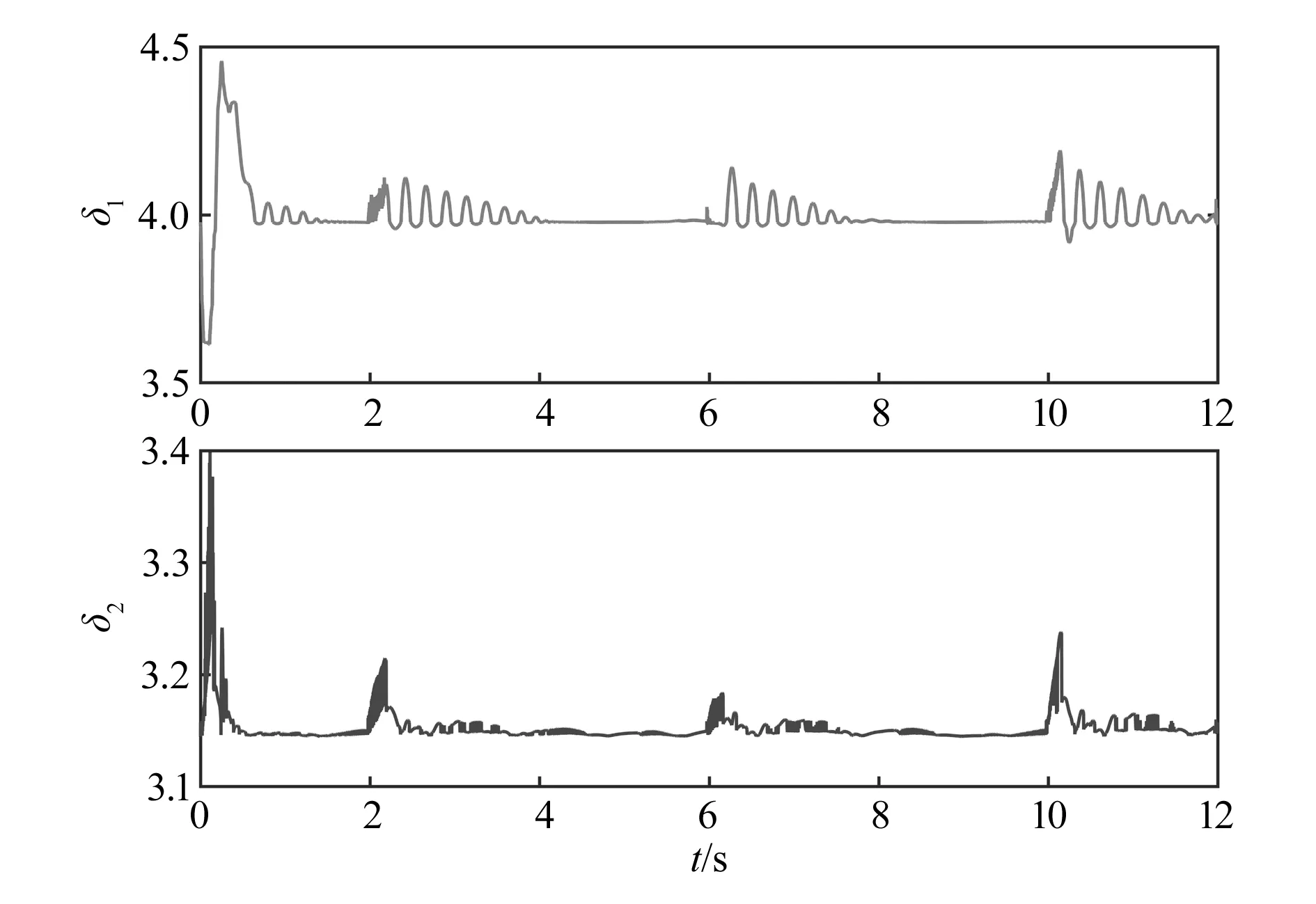
图7 工况1模糊量

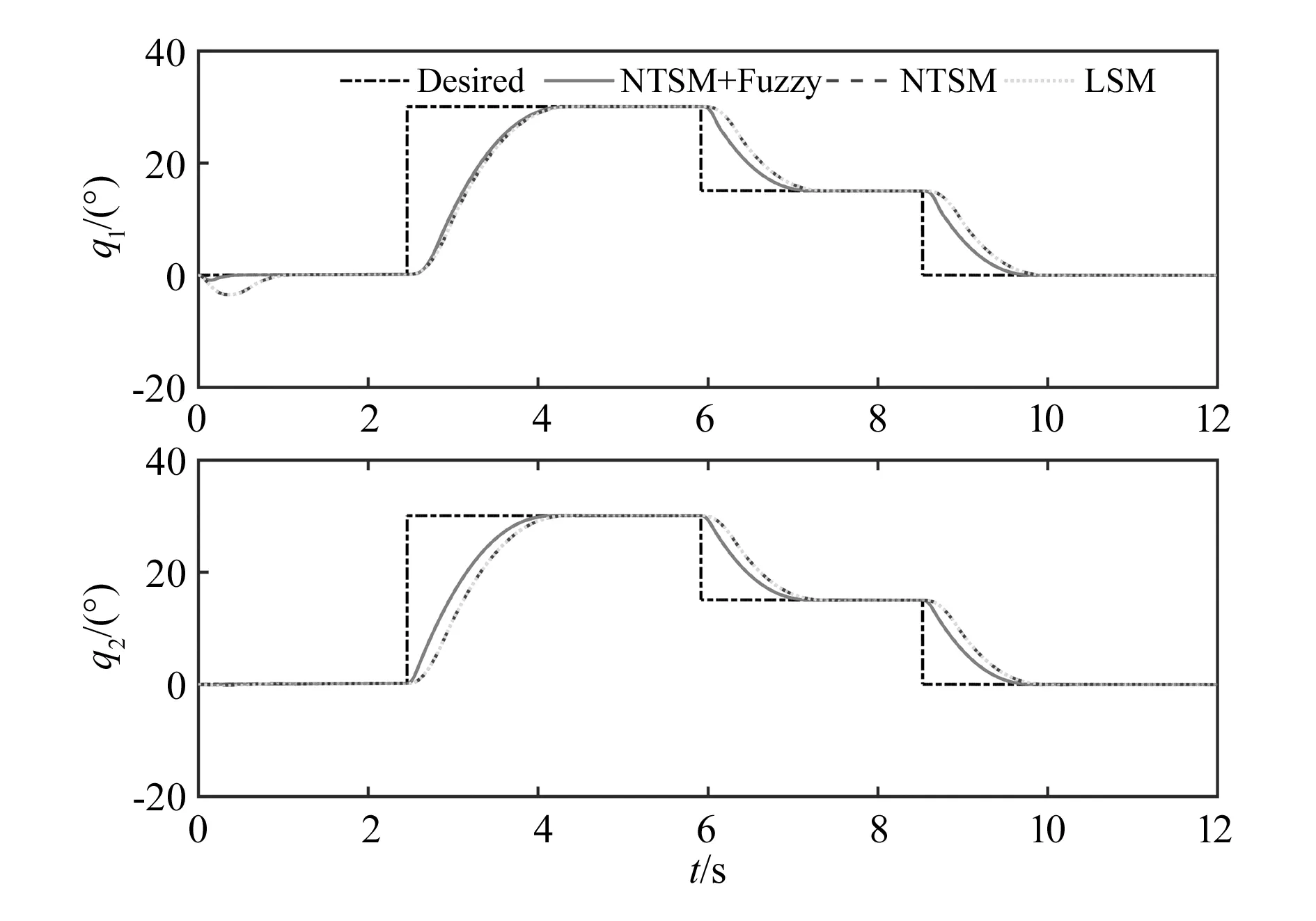
图8 工况2关节跟踪轨迹

图9 工况2关节跟踪误差

图10 工况2关节跟踪力矩

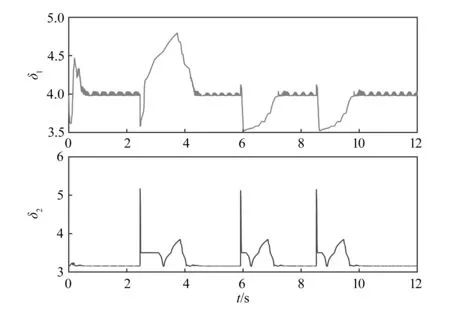
图11 工况2模糊量

从工况1、工况2的关节轨迹跟踪图可以看出，绳驱动机械臂关节运动在NTSM-Fuzzy控制器下对理想轨迹的拟合性更好，证明了其优越性。从关节跟踪误差图可以看出，当机械臂处于开始和换向阶段时系统误差放大，但由于引入了模糊控制项δ，误差e的增大使输出的δ也相应地增大，从而抑制了误差，由此可以看出本文所设计的NTSM-Fuzzy控制器的有效性。对比关节跟踪力矩可以看出，NTSM-Fuzzy控制器下的关节力矩波动较大，说明良好的控制效果也是以牺牲更多的关节力矩为代价得到的。

以关节1为例，从关节的控制误差指标Rms与Max值可以看出。工况1在NTSM-Fuzzy控制器下均方差Rms减小了85%左右，峰值误差Max减小了75%左右，证明了NTSM-Fuzzy控制器的鲁棒性。虽然在工况2下NTSM-Fuzzy控制器的控制效果与其他控制器的控制效果对比优势不明显，但也还算差强人意。

5 结束语

为了增加旋翼飞行器主动作业能力，本文设计了一款可供旋翼飞行器搭载的轻量化绳驱动机械臂。设计了一款基于时延估计的模糊非奇异终端滑模控制器，用于绳驱动机械臂的运动控制。通过李雅普诺夫理论，证明了控制器的稳定性与误差收敛性。最后在两种工况下，设计对比仿真实验，验证了所设计控制器的有效性、鲁棒性。

下一阶段将针对绳驱动机械臂空中作业能力进行研究。在多干扰、多自由度的集成环境下，可能需要改进机械臂的控制方法，减少作业误差，高效完成空中作业。