抛物线轴类零件数控加工参数远程调试系统设计
苏志雄
(福建省湄洲湾职业技术学校,福建 莆田 351100)
抛物线轴类零件是数控加工中常见的零件,其具有旋转体的特性,加工时通常需要精细的参数控制,甚至需要进行额外的参数调试。然而,许多系统的显示时间与执行时间存在差异。为了优化工作效果,需要一个更好的远程调试系统。文献[1]基于QT(应用程序开发框架)平台,设计了一种操作简单、扩展性较强的参数远程调试系统,避免了雷达伺服调试过程中指令复杂的问题,提高了调试的工作效率。但是该系统着重于软件系统和硬件系统的衔接,虽提高了普适性,却没有详细设计更简便的程序,导致系统运行时间较长;文献[2]研究了一种基于信号数据接口的机构运动学建模与解算模块的自动化平台,提高了系统的并行计算能力,使多种虚拟调试参数能够被并行操作,但该系统过于精密,导致生产周期和制造成本均高于其他系统,难以被广泛使用;文献[3]提出了一种基于移动互联网的终端调试系统,工作人员能够在后台直接调试终端机中的各项参数,提高了调试工作的效率,该系统运用在数控加工领域,可以极大地提高工作效率,使每一个工作人员都能够独立运行主机和终端数控加工机床,但是该系统只注重数控加工软件程序的改良,没有做好软件与硬件的衔接工作,使得硬件系统难以匹配软件的工作效率,系统运行速度较慢。
本文设计了一种抛物线轴类零件数控加工参数远程调试系统,结合加工轴类零件的一阶数学模型、二阶数学模型、一阶离散控制模型、二阶离散控制模型,解决了数控加工参数远程调试系统执行时间与显示时间差异大的问题。
1 抛物线轴类零件数控加工参数远程调试系统设计
1.1 抛物线轴类零件特征参数化
大多数抛物线轴类零件的三维特征为其多个子节点组成的特征集,即:
Ki={m1,m2,…,mn}
(1)
式中:Ki(i=1,2,…,k)为抛物线轴类零件中的第i个零件;mi为零件的第i个特征,分别为轴段、倒角、键槽、中心孔、径向孔、轴向孔、退刀槽、锥轴、螺纹、台肩和圆角,以及齿轮轴、蜗杆和花键等特征类型[4-5],其中mn是该零件的第n个特征,也是最后一个特征[6-7]。每一个特征都可以建立一个特定的特征参数化表达式:
Mn={hn1,hn2,…,hnf}
(2)
式中:Mn为该抛物线轴类零件结构中第n个特征的参数化形式;hn1,hn2,…,hnf为特征集合中的若干个参数,其中hnf为第f个参数,也是最后一个参数。这里的参数主要为抛物线轴类零件的精度、尺寸、质量等信息[8-9]。整理以上参数,可以通过输入与输出序列,并结合最小二乘法得到观测矩阵的计算增益函数:
(3)
式中:Hn(f)为抛物线轴类零件结构中第n个特征的参数化增益函数;μ(x)为协方差矩阵的最初赋值;T为矩阵计算的时间常数;an(x)为可调节系数;bu(x-1)为属性描述函数,u为相位延迟系数。通过以上公式,可以将所有抛物线轴类零件中的各项特征全部参数化,优化多模型拟合过程[10-11]。
1.2 远程调试目标优化
在系统的远程调试过程中,需要明确约束条件和优化目标,以确保远程调试目标优化结果的唯一性和可行性。
设影响数控加工参数远程调试精度的影响因子为Xp={x1,x2,…,xp},p为影响因子总数量。在设定优化目标时,要求参数精度最大化,即读取、传输、导入的调试目标函数为最小值:
(4)
式中:ak(x),bk(x),ck(x)为被控制参数x的读取、传输、导入的调试目标。以此寻找满足最优调试精度的子目标函数[12-13]。在等效替换过程中,将所有远程调试目标优化通过以下形式统一表达:
(5)
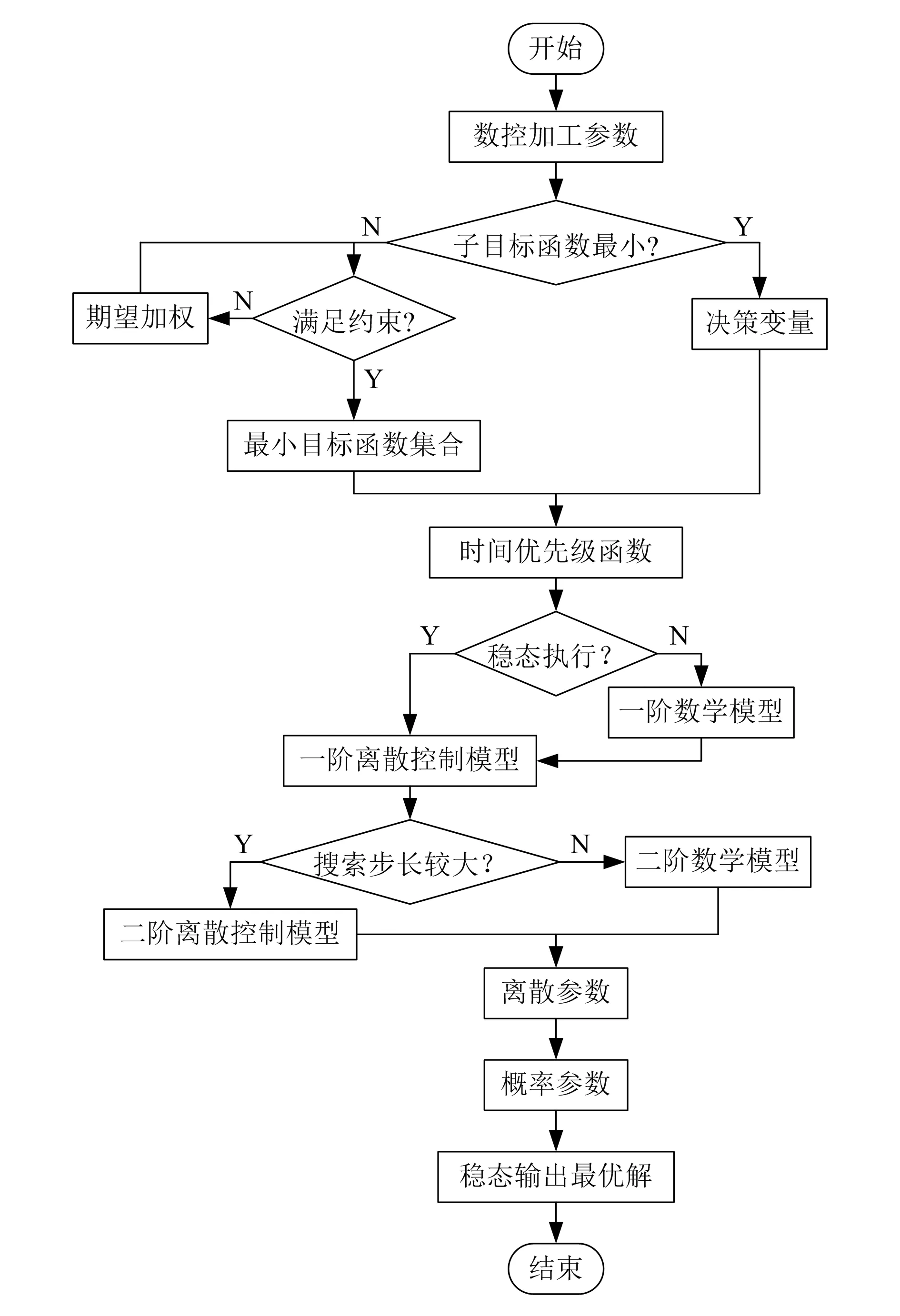
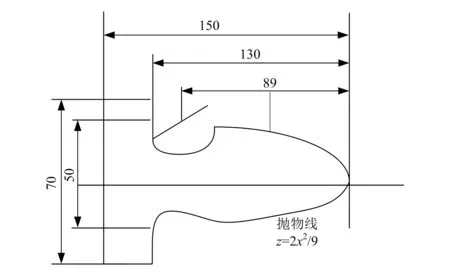
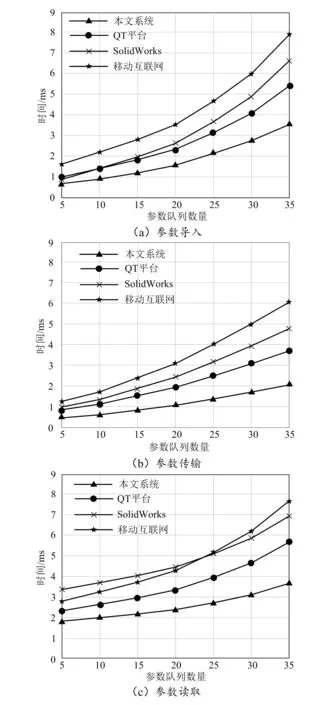
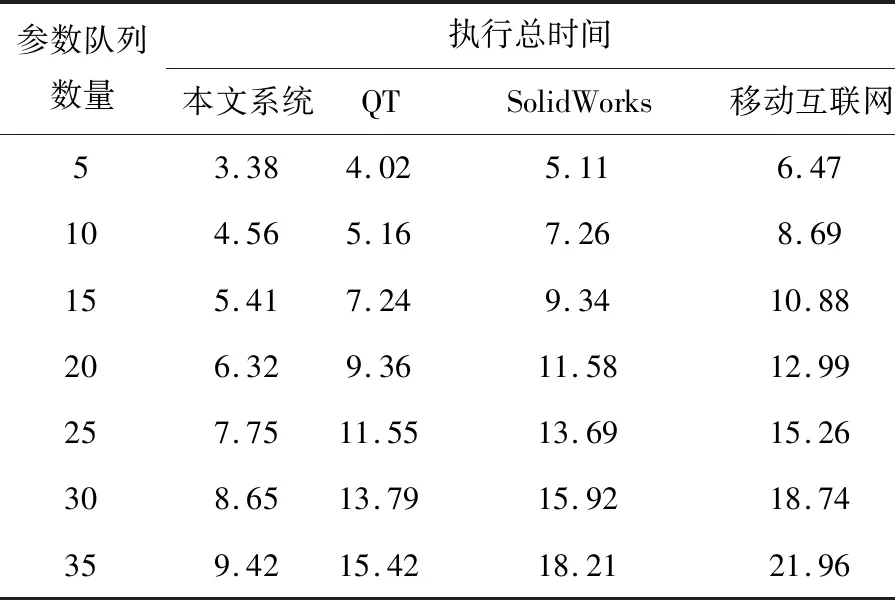
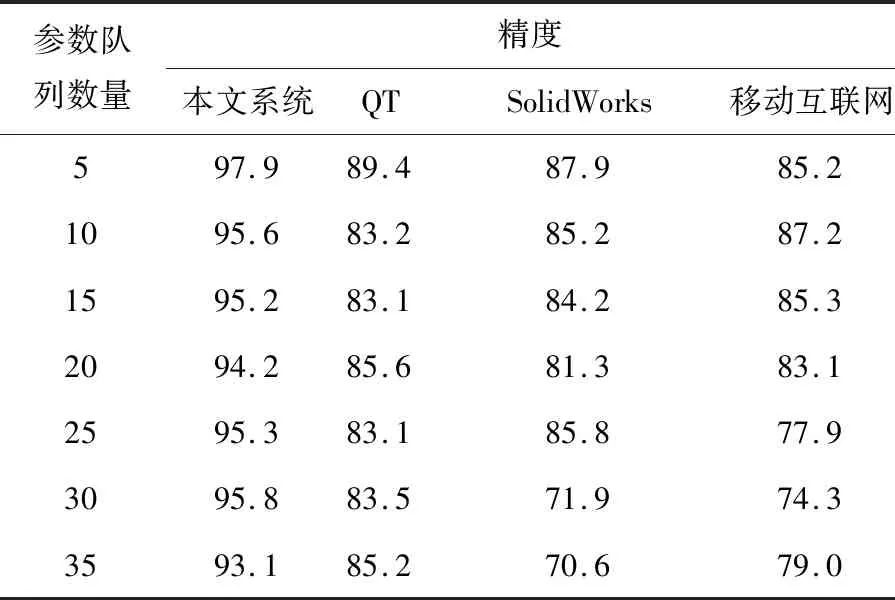
式中:{f1(a),f2(a),…,fn(a)}为所有的远程调试参数;f1(a) 现有的许多抛物面轴类零件数控加工参数远程调试系统无法有效地调整多个队列的排列方式,导致系统多个队列数据一起处理时,容易产生拥塞,影响参数传输的速度,参数导入与初始读取参数个数不匹配[14]。此时,需要将以上特征和参数均设置在一个编码结构中,建立一个参数调试的时间优先级函数,即保证调试结果为最优解。 为每一个参数,设定唯一决策变量,即取最小值: Xp=min{x1,x2,…,xp} (6) 式中:Xp为每一个零件的特征参数决策变量集合;x1,x2,…,xp分别为每个参数所代表的决策变量。 在制定决策变量之后,需要计算加工轴类零件的一阶数学模型、二阶数学模型、一阶离散控制模型、二阶离散控制模型。由于零件的参数是随机的,轴类零件的一阶数学模型an(x)为: (7) 轴类零件的二阶数学模型an(x-1)为: (8) 式中:ξ为阻尼系数;ω表示二阶导数。 加工轴类零件的一阶离散控制模型bu(x)可表示为: (9) 式中:xu为零件的离散参数;Ru为时间型线性连续离散量;Ku为状态型线性连续离散量。 加工轴类零件的二阶离散控制模型bu(x-1)可表示为: (10) 在以上模型的基础上,重新构建1.1中三维特征子节点的读取函数: an(x)+an(x-1)=bu(x)+bu(x-1) (11) 计算参数读取队列优先级反转的概率: (12) 式中:Pd为抛物线轴类零件参数读取队列优先级反转的概率;pn为优先级靠前的轴类零件参数优先级反转的概率;ph为优先级靠后的轴类零件参数优先级反转的概率;Hv为系统中支持的最大优先级参数;th为优先级靠前的轴类零件参数优先级反转所用时间;tn为优先级靠后的轴类零件参数优先级反转所用时间;thm为等待优先级反转的总时间。 轴类零件参数队列需要经过输入、输出、执行3个步骤,分别对应调试参数在输入端口的程序导入、调试参数在两个主机之间的传输、调试参数被数控机床读取。在此基础上,构建轴类零件参数队列稳态执行函数,使其满足所有状态平衡的介入: (13) 式中:σd和σd-1表示任务加工的过程中参数σ在处于导入状态d与处于d状态前一刻达到平衡的时间;σc,σc-1和σc+1分别表示参数σ在传输状态c时、c状态前一刻、c状态后一刻达到平衡的时间;σq和σq+1表示参数σq在读取状态q时和q状态后一刻达到平衡的时间[15]。在整个平衡过程中,可以通过期望加权获得队列的平均等待时间: (14) 式中:Td为队列的平均等待时间;ωi为队列中等待远程调控的参数个数。遍历各个排列组合中Td的数值,选择其中最小的一个,即为多队列轴类零件参数调试最优解。 多队列轴类零件参数调试最优解获取流程,即单一抛物线轴类零件数控加工参数远程调试流程如图1所示。 基于图1,即可得出某个抛物线轴类零件数控加工参数的远程调试结果,整合多个最优解,完成抛物线轴类零件数控加工参数远程调试目标。 图1 多队列轴类零件参数调试最优解获取流程 为了检测该系统中参数执行时间与参数响应时间的差距,对其进行测试,并与基于QT平台的调试系统(文献[1]方法)、基于SolidWorks的调试系统(文献[2]方法)、基于移动互联网的远程调试系统(文献[3]方法)进行对比,分别测试4种系统的数据传输与显示的能力。 以YG8硬质钨钢合金精磨销钉为测试对象。为了保证测量精度,使用零部件模件检测仪AX8200MAX X-Ray作为检测设备测量该销钉尺寸,销钉质量为1.02 kg,尺寸如图2所示。 图2 销钉尺寸 根据图2尺寸,建立图3所示的编程坐标系。 图3 零部件加工过程的编程坐标系 虽然该零件的加工工艺相对较简单,但是其抛物线部分仍需要采用节点拟合方法加工,该方法可以获取较为准确的测试结果。 使用MATLAB中的线性时不变浏览器LTI Viewer绘制系统的阶跃响应、脉冲响应、开环伯德图等特性曲线,利用MATLAB控制系统工具箱中的SISO设计器直接生成Simulink仿真模型。在MATLAB工作空间中,通过信息传输通道,将调试窗口的数据传送到PC(personal computer)端,并以图形或图像的形式显示出来。 调试窗口中的信号阈值是恒定不变的,在频域振幅为零时,系统的稳态精度达到123 Hz,相频宽度达到80 Hz。在计算参数远程调试系统的任务时间时,需要首先假设系统中的复指数分布就绪,然后根据1.3节的参数调试时间优先级函数模型公式(13)和公式(14),其参数调试的执行时间可以通过公式(15)计算: (15) 式中:md,mc,mq分别为参数在导入、传输、读取的时间内经过单位队列时所需的时间。 在以下实验中,分别测试导入、传输、读取3个步骤所需要的时间,并记录不同参数体积下远程调试所需要的总时间: tm=t1+t2+t3 (16) 式中:tm为不同参数体积下远程调试所需要的总时间;t1为调试参数在输入端口的读取导入时间;t2为调试参数在两个主机之间的传输时间;t3为调试参数被数控机床读取时间。再计算参数在显示端显示的时间: (17) 式中:Tx为参数传输到PC端并显示所需的时间;ni为第i个参数队列的数据长度;σi为传输第i个参数队列所需时间。通过式(15)、(16)、(17),可以得到4个系统中数据执行与数据显示时间的比较结果。 以参数的队列数量为变量,由式(16)分别得到4个系统在参数导入、参数传输、参数读取3个步骤中所需要的时间,如图4所示。 图4 参数远程调试系统执行时间测试 由图4可知,在参数队列逐渐增加的情况下,各系统在参数远程调试时所使用的时间也在不断增加。在参数导入时间的测试中,不同参数队列下,本文系统的读取时间均少于其他3个系统。在参数传输与参数读取的时间测试中,不同参数队列下本文系统用时也少于其他3个系统。结合图4与式(17),可以计算参数远程调控系统执行的总时间,具体见表1。 由表1可知,当参数队列数量逐渐增加时,4个系统需要的执行时间也逐渐增加,但本文设计的系统所需要的时间少于其他3个系统。除参数的导入、传输、读取外,实验参与者通过PC端口观察到参数也需要一定的时间。远程调试系统显示时间测试结果如图5所示。 表1 参数远程调试系统参数执行总时间 单位:ms 图5 参数远程调试系统显示时间 由图5可知,随着参数队列数量的增加,4个系统将参数通过屏幕显示出来的时间也在增加,但是相比执行总时间,显示时间更少,以35个参数队列为例,4个系统的参数显示时间分别约为9.02 ms、12.78 ms、16.14 ms、17.92 ms,与表1数据对比,可见本文系统执行总时间与显示时间的差异最小。由此可见,本文设计的系统在调试系统时可以有更好的效果。 参数队列数量越多,越容易影响参数精度,因此以参数的队列数量为变量,通过公式(4)和公式(5)获得4个系统在参数导入、参数传输、参数读取过程中不同参数量下远程调试总精度为: αm=α1+α2+α3 (18) 式中:αm为不同参数队列数量远程调试的总精度;α1为读取精度;α2为传输精度;α3为执行精度。 通过式(18)分析参数远程调试系统参数精度,见表2。 表2 参数远程调试系统参数精度 % 由表2可以得知,参数队列数量逐渐增加时,4个系统的精度都在逐渐下降,但本文设计的系统精度均在90%以上,高于其他3个系统,表明该调试系统具有较好的应用效果。 本文设计了一种抛物线轴类零件数控加工参数远程调试系统,通过一阶数学模型、二阶数学模型、一阶离散控制模型、二阶离散控制模型的交互控制构建时间优先级函数,计算多队列轴类零件参数调试时间最优解,以保证参数远程调试系统参数执行总时间、显示时间较少,整体参数精度均在90%以上。 但是极小化的目标函数受到期望加权完工时间、期望加权误工时间及期望加权误工工件数等多变量的影响,而设计的抛物线轴类零件数控加工参数远程调试系统尚不全面,因此在未来的研究中,将扩大变量,增加实验样本,争取为该领域的相关研究提供更多有价值的参考。1.3 多队列轴类零件参数调试最优解
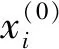
2 实例测试与结果
2.1 测试准备

2.2 执行时间与显示时间的差异测试

2.3 加工精度测试
3 结束语

