钢板组合梁温度作用的极值统计模型
闫新凯 刘永健,2 刘 江 白永新 张宸瑜 马志元
(1长安大学公路学院, 西安 710064)(2长安大学公路大型结构安全教育部工程研究中心, 西安 710064)
桥梁长期承受太阳辐射、气温变化和风等自然因素循环往复作用,结构内部温度场不断变化,产生温度变形和约束应力,极端条件下温度作用可能超越恒、活载成为第一控制作用[1-3].为保证桥梁的可靠性,需要确定温度作用的模式和取值,在设计阶段进行结构验算.公路工程结构采用以概率理论为基础的极限状态设计法,对于由自然因素产生的桥梁温度作用具体分析时可将一定时段内的最大值视作随机变量,通过统计分析得到一定重现期对应的温度作用代表值[4].然而,现有规范主要依据桥梁所在地区的极端气温确定温度作用取值,概率意义不明确[5-6].
桥梁温度作用样本有3种来源:试验测试、数值模拟和气象相关性公式计算.文献[7-19]通过数月到几年的试验测试得到温度作用样本,统计分析计算代表值.实测过程一般难以得到足够的年极值样本,文献[20]基于日极值底分布,采用Monte-Carlo法模拟了100 a的日极值数据,取年极值统计;该方法实质上是在利用日极值分布计算年极值分布时,以抽样模拟替代了数学解析过程,日极值样本较少,难以准确估计真实分布.试验测试需要耗费巨大资源,测试规模和时长受限,数值模拟为获取桥梁温度作用样本提供了一种更高效的方法.文献[21]利用5%超越概率的太阳辐射量计算桥梁竖向温差,没有考虑其他气象参数的统计特性.文献[22-24]根据太阳辐射、气温、风速等极端气象条件计算桥梁温度梯度,由于计算过程中认为气象参数极值同时出现,导致计算结果偏大.文献[25-26]直接将气象参数时程代入有限元模型,进行桥梁温度场的长期计算,得到统计样本,使计算结果更加准确,但是数值模拟的运算量大.桥梁温度作用与气象参数具有显著的相关性[27-28],利用温度作用的气象相关性公式可以极大地降低运算量.将气象参数的联合概率分布代入公式可以解析计算出温度作用的概率分布.文献[29-30]通过高斯积分法计算了温度作用的前4阶矩,认为其服从Gumbel分布,数理性不够严谨,因为数值积分足够精确的前提是气象相关性公式为低次幂函数,且仅通过偏斜度和峰度不足以判定温度作用服从Gumbel分布.文献[31-32]直接将气象数据代入相关性公式,得到温度作用样本.
温度样本采用基于广义极值分布(GEVD)的区组模型和基于广义帕累托分布(GPD)的超阈值模型2种极值统计模型.文献[7-10]基于不同国家、地区的桥梁温度样本,采用Gaussian分布、Gumbel分布和Weibull分布等作为温度极值的概率模型.按极值统计理论,独立同分布随机变量序列的最大值近似服从GEVD分布[33].文献[11-17]应用GEVD分布进行温度极值的概率统计,Gumbel分布和Weibull分布属于GEVD分布的特例.此外,独立同分布随机变量序列的超阈值近似服从GPD分布[33],文献[6,18-19]利用GPD分布统计了温度超阈值样本的概率分布.GEVD分布和GPD分布分别取区组极值和超阈值统计,文献[34-35]认为GPD分布计算结果更优,但尚未在桥梁温度作用统计中进行对比.
钢-混凝土组合梁由2种热工和力学性能差异较大的材料组成,温度效应更为显著[36].桥梁有效温度的变化将引起结构纵向伸缩变形,控制着伸缩缝、支座甚至桥墩的设计与选型[2],有效温度的准确取值是合理设计的重要前提.本文在系统梳理桥梁温度作用统计方法的基础上,基于3类样本和2种统计模型计算了钢板组合梁的有效温度代表值,比较分析了各方法的优缺点和适用性,以期为类似研究提供参考.
1 桥梁温度作用代表值计算方法
已知试验测点或有限元节点的温度,组合梁有效温度的计算公式为[28]
(1)
式中,Te为有效温度;Ti为第i个测点或有限元节点的温度;Ai、Ei分别为第i个测点或有限元节点的区域面积和材料弹性模量.
桥梁温度受气象参数影响在日和年2个尺度上表现出明显的周期性,需要降低温度序列间的相关性.通常取日极值消除日周期性[20],对于年周期性,基于历史气象数据的数值模拟和公式计算取年极值即可.试验测试一般仅有数月到几年,没有足够的年极值样本,常用极值指标修正[16,27]、聚类分析[10]和因素分离[8-9,17]等方法对日极值样本进行处理.因素分离法将温度测试值分为确定部分和随机部分,确定部分是将以年为周期的规律性变化部分通过函数拟合确定的,测试值与确定部分的差值为随机部分,对随机部分进行统计分析.本文采用该方法处理试验测试的有效温度日极值样本,按三角函数拟合确定部分为
(2)
式中,Td为规律性变化的温度;td为日序数;A、B、C为待定参数.
去相关性后的温度样本可采用区组模型和超阈值模型来统计概率分布,推算温度作用代表值[4,33].最低有效温度需取相反数作为统计样本[15],试验测试样本需将确定部分的极值与随机部分推算的极值叠加.计算公式为
(3)
(4)
式中,Fl(x)为l天内温度作用最大值的概率分布函数;l对于区组模型为区组间隔,对于超阈值模型为超阈值平均出现时间间隔;M为重现期;Tp为具有保证率p的极值温度.
当温度作用服从GEVD分布时,极值温度为
(5)
式中,k、μ、σ分别为形状参数、位置参数和尺度参数.
当温度作用服从GPD分布时,极值温度为
(6)
根据数据来源可将温度作用样本分为试验测试、数值模拟、气象相关性公式计算3类.其中,试验测试样本直接由实桥或模型测试得到,数据最有效、可信,但是样本量通常较小.数值模拟样本和气象相关性公式计算样本均是基于气象数据得到温度作用,充分利用了气象站点记录的丰富历史气象数据.数值模拟样本是通过开展长期温度场模拟得到的长时间周期内的温度作用样本,计算量较大,且数值模拟的准确性需要得到充分验证.气象相关性公式计算样本是由温度作用与气象参数间相关性公式计算得到的温度作用样本,前提是建立的气象相关性公式准确.表1给出了这3类温度作用样本的特点.

表1 三类温度作用样本的特点
区组模型取每个区组的极大值进行统计.由于存在一个区组内可能包含多个极值的情况,故对极值信息的利用率不高.超阈值模型取超过某一阈值的极值进行统计.2种模型对比见表2.虽然超阈值模型对极值信息利用率更高,但是成串出现的极值具有较强的相关性,对统计结果不利.

表2 区组模型与超阈值模型对比
温度作用日极值的随机部分仍具有一定的相关性,可通过自相关系数R(m)度量,使自相关系数接近于零的区组间隔,区组极值可认为是平稳时间序列[18].计算公式为
(7)
式中,xj和xj+m分别为tj和tj+m时刻的样本观测值;xa为样本均值;m为区组间隔;n为样本容量.
采用超阈值模型进行极值分析时,若选择的阈值过大,样本较少,导致估计量方差较大;阈值过小,样本不一定服从GPD分布[33].可通过计算平均超出量函数S(u)来确定阈值,即
(8)
式中,yi为超过某阈值的样本观测值;Nu为超阈值u的样本容量.
如果对应某个阈值u0的超阈值样本服从GPD分布,则对于u>u0,平均超出量函数呈直线[11].由于对线性变化的判断具有主观性,为降低由此产生的误差,本文计算了平均超出量近似呈线性变化的区段内各阈值对应的极值温度,并将其取平均值.
2 钢板组合梁模型温度测试
2.1 试验
试验场地位于青海省黄南地区,东经102.23°,北纬35.3°,海拔2 150 m,在中国气候分区图中属于严寒地区[5].试验模型为一工字形钢板组合梁节段,长3 m,高1.5 m.以距梁端L/3处的截面作为测试断面.在现场设立了小型气象站,记录太阳辐射、气温和风速等气象数据.测试时间为2017-04-01—2018-06-30,共计456 d,测试时间间隔为20 min.由于电源及设备故障等原因,2017-05、2017-10、2018-12—2018-02的温度数据存在缺失.试验模型、测点布置的详细情况参见文献[37].
2.2 气象测试结果
图1给出了太阳辐射和气温的实测数据.由图1(a)可知,水平面接收到的日总太阳辐射量H具有明显的季节性变化特征,夏季辐射最强,冬季辐射最弱.由图1(b)可知,日最高气温Tamax和日最低气温Tamin均呈现出年周期性变化,在局部较短时段内又表现出随机性.日平均风速v没有出现明显的周期性.
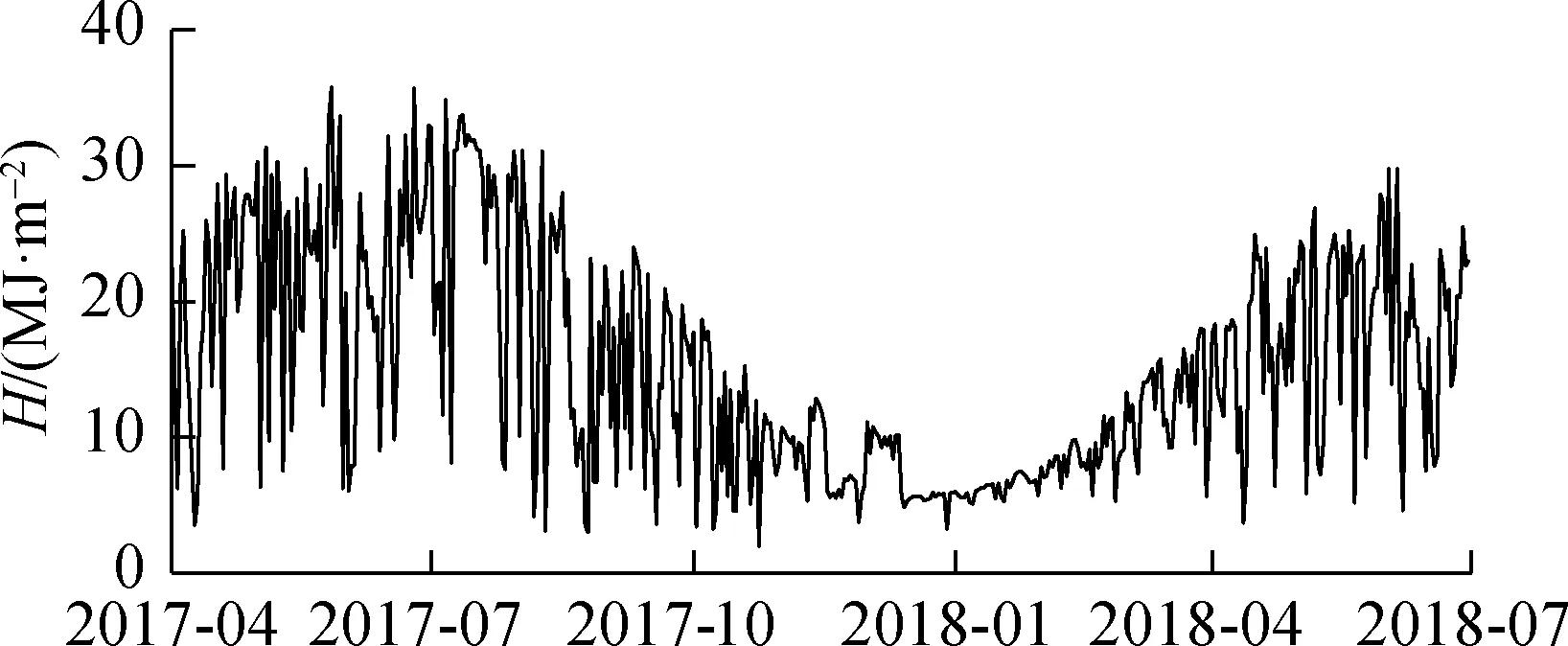
(a) 水平面日总太阳辐射量
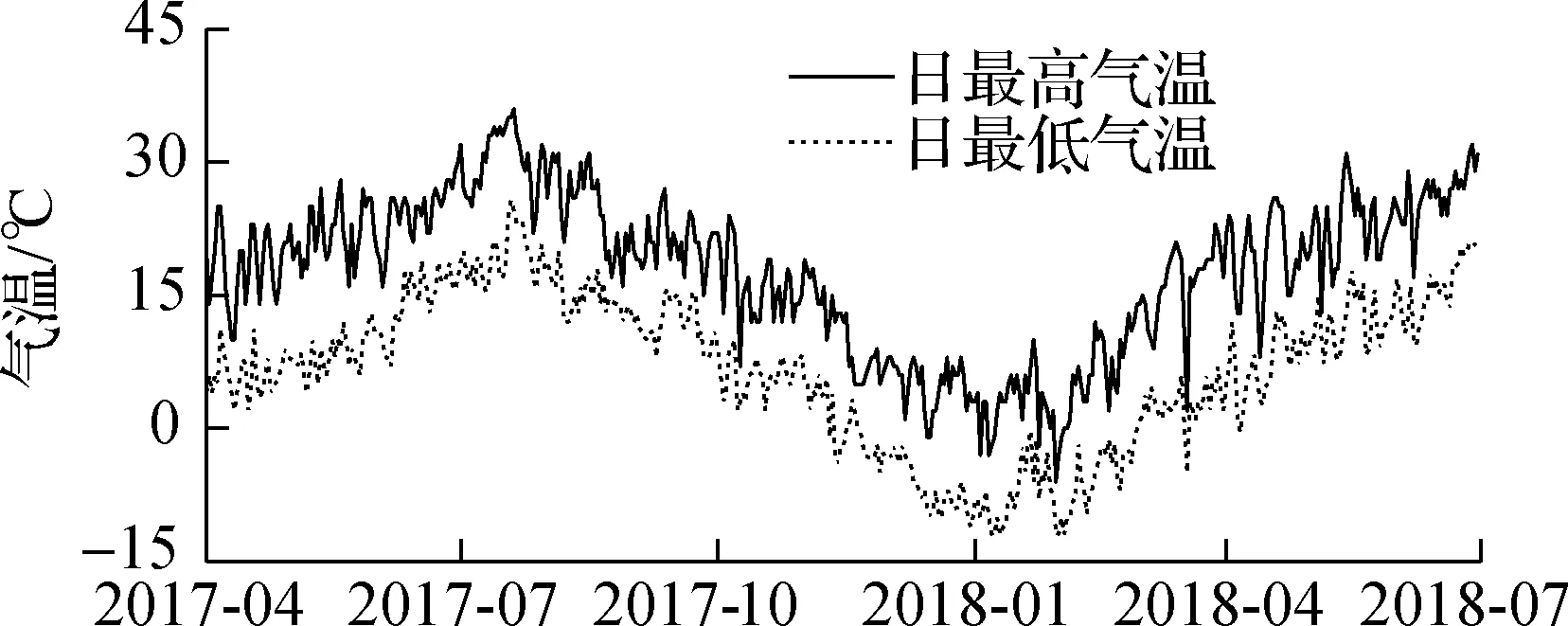
(b) 气温
3 温度场数值模拟
3.1 历史气象数据
从国家气象科学数据中心收集了距离试验场址最近的辐射气象站点(青海省西宁气象站)1993-01-01—2015-12-31的气象数据,包括水平面日总太阳辐射量H、日最高气温Tamax、日最低气温Tamin以及日平均风速v.
3.2 逐时气象数据
根据经验公式,将以日为单位记录的气象数据转换为逐时气象数据,得到可代入有限元模型计算的热边界条件[37].
3.2.1 太阳辐射强度
根据水平面日总太阳辐射量H,计算各时刻水平面总太阳辐射强度Ig为[38]
(9)
式中,τ为时角;τs为日落时角;a、b为系数.
由水平面总太阳辐射强度Ig计算水平面太阳直射强度Ib和散射强度Id为[39]
(10)
式中,τb、τd分别为直射和散射透射比.
3.2.2 气温
为避免仅以当日气温极值拟合导致温度在0点时不连续[22,24],假定日最低和最高气温分别发生在6:00和15:00,按下式拟合各时刻气温Ta(t):
(11)
式中,t为当地真太阳时;Taminp为次日的最低气温.
3.2.3 对流换热系数
将一天内的风速认为是恒定值,取为日平均风速,则对流换热系数hc为[40]
(12)
3.3 有限元模型
采用ABAQUS程序,建立组合梁瞬态热传导温度场二维平面有限元分析模型.混凝土板和钢梁均采用程序中提供的四节点线性四边形传热单元(DC2D4),钢-混凝土界面采用绑定约束模拟第四类热传导边界条件.钢梁部分区域接收太阳辐射会受到桥面板的遮挡,按几何关系确定钢梁阴影高度,计算公式参见文献[24].编写DFLUX子程序施加太阳辐射,并自动判定混凝土板对钢梁的辐射遮挡区域.有限元模型以及材料的热工参数详见文献[37].
3.4 模型验证
将试验期间实测的气象数据按3.2节中的方法转换为逐时数据,代入有限元模型,对试验期间的截面温度场进行模拟计算,计算时间间隔为1 h.日最高和最低有效温度的有限元计算结果与实测值的决定系数R2均大于0.97,平均绝对误差(AAE)和均方根误差(RMSE)均小于1.5 ℃[28],说明该有限元模型较为准确.日最高有效温度有限元计算结果与实测值对比见图2.由图可知,数据点集中在y=x附近.
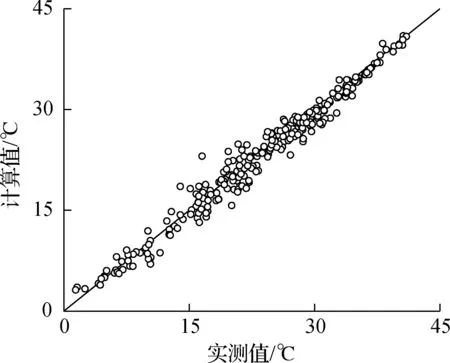
图2 日最高有效温度有限元计算结果与实测值对比
4 气象相关性公式
文献[1-3]指出,特定桥梁的温度作用主要与气温、太阳辐射和风速等气象参数有关.虽然以往学者多将有效温度变化归结于年气温变化,但是通过计算对比发现忽略太阳辐射会低估组合梁的有效温度.因此,本文建立了日最高有效温度Temax与日最高气温、日温差以及太阳辐射间的相关性公式,和日最低有效温度Temin与日最低气温、日温差间的相关性公式,即
(13)
拟合公式(13)中R2均大于0.96,AAE和RMSE均小于1.5 ℃,说明拟合效果较好.
5 温度作用代表值计算
5.1 基于试验测试数据的计算
采用因素分离法将实测温度作用日极值分解成确定部分和随机部分.图3给出了日最高有效温度及其确定部分和随机部分.由图可知,实测最高有效温度为40.99 ℃,确定部分的最大值为31.88 ℃,随机部分不再具有明显的周期性变化特征.实测最低有效温度为-8.91 ℃,确定部分的最小值为-2.77 ℃.由于缺失冬季部分测试数据,故最低有效温度可能较实际情况偏高.
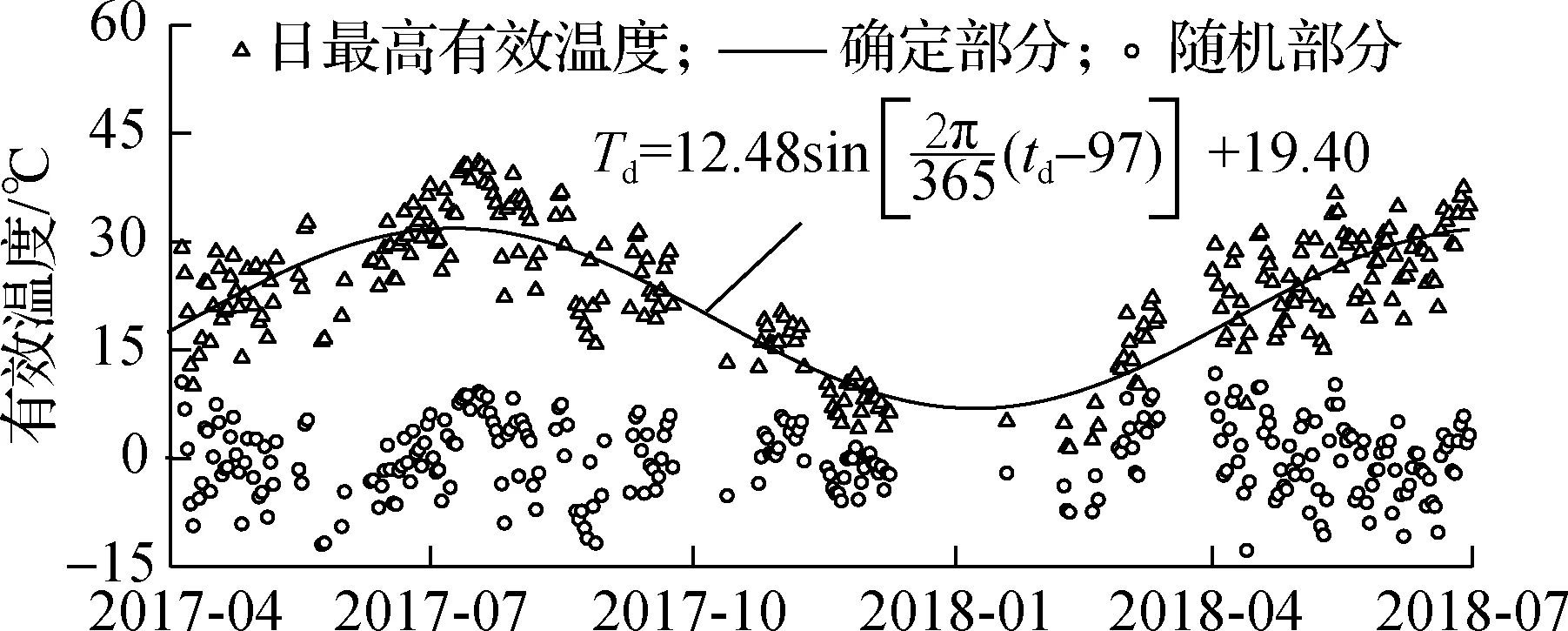
图3 实测日最高有效温度时程曲线
图4给出了不同区组间隔下随机部分时间序列的自相关系数.当区组间隔为14 d时,自相关系数接近于0.每隔14 d取最大值,日最高和最低有效温度的样本量均为23,按GEVD分布拟合均服从极值Ⅲ型分布,分布参数(k,μ,σ)分别为(-0.451 6,5.513 4,3.267 9)和(-0.463 6,3.062 0,2.325 3),均通过了显著水平为0.05的Pearsonχ2检验.图5给出了日最高有效温度区组极值拟合结果.

图4 自相关系数

图5 实测日最高有效温度的GEVD拟合结果
日最高和最低有效温度随机部分的平均超出量均在阈值为0~6 ℃间近似呈线性变化,在该范围内取不同的阈值计算极值温度,重现期为100 a的结果见图6.由图可知,极值温度的变化范围很小.最高和最低极值温度最接近平均值的阈值分别为2.75和1.00 ℃,样本量分别为89和114.超阈值数据按GPD分布拟合均服从帕累托Ⅲ型分布,最高和最低有效温度分布参数(k,μ,σ)分别为(-0.433 7,2.75,4.203 4)和(-0.335 4,1.00,2.545 9),均通过了显著水平为0.05的Pearsonχ2检验.图7给出了日最高有效温度随机部分超阈值的拟合结果.

图6 不同阈值计算的极值温度
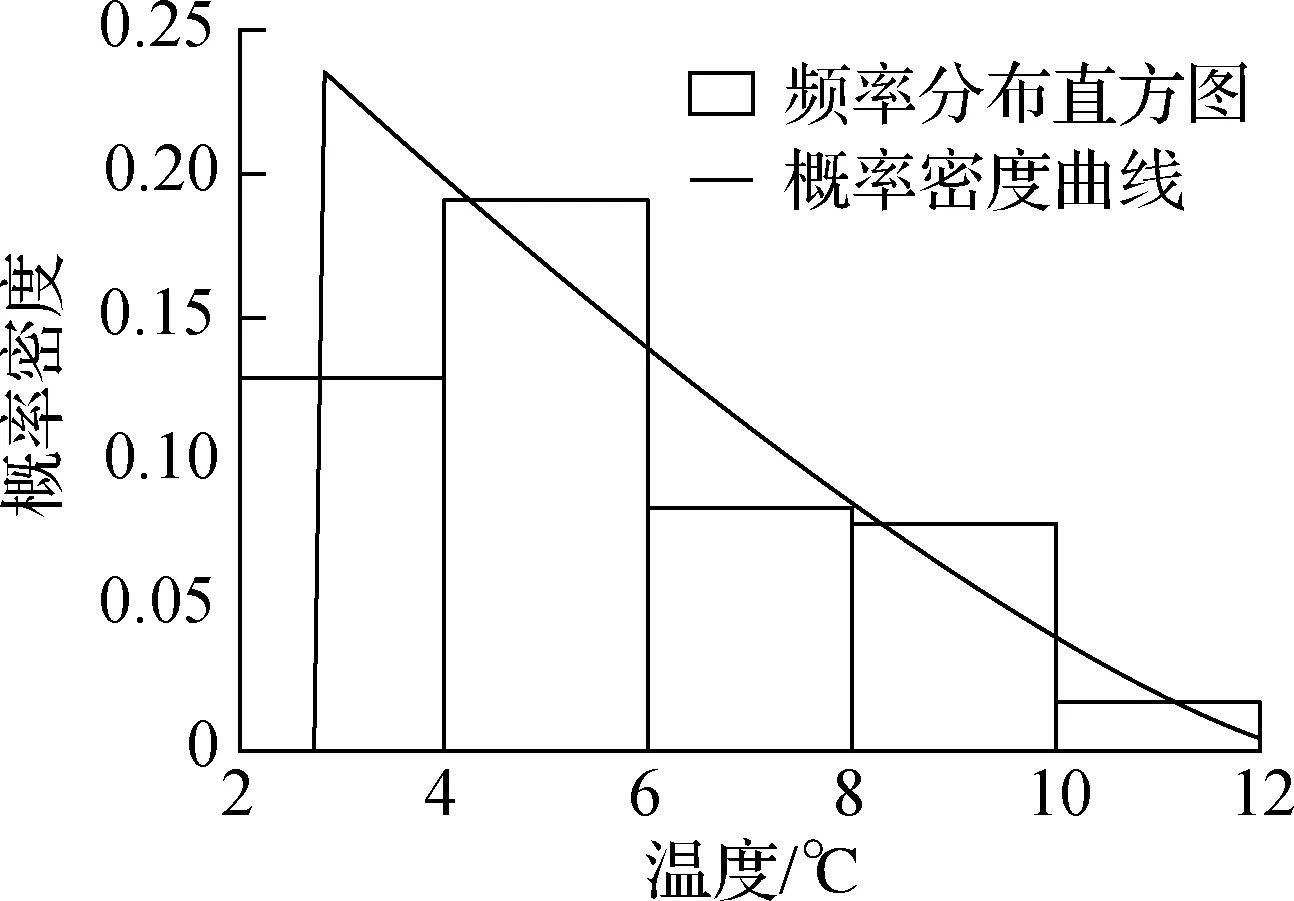
图7 实测日最高有效温度的GPD拟合结果
表3给出了基于试验测试数据计算的最高和最低有效温度代表值.实测1.25 a的最高和最低有效温度分别为40.99和-8.91 ℃.由表可知,区组模型和超阈值模型推算结果相近,均大于1.25 a实测极值.
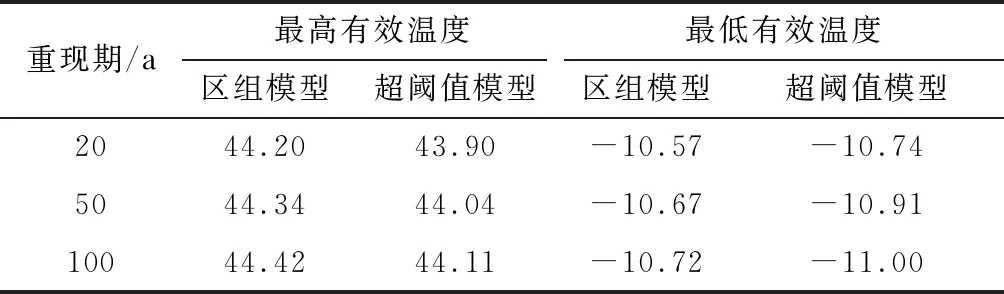
表3 基于试验测试计算的有效温度代表值 ℃
5.2 基于长期数值模拟的计算
将历史气象数据代入有限元模型进行温度场的长期计算,计算时间间隔为1 h.图8给出了日最高和最低有效温度以及各年的最高和最低有效温度.由图可知,有效温度呈年周期性变化,每年变化范围相近,年最高和最低有效温度分别为37.83~45.04和-12.83~19.58 ℃.在高于40 ℃和低于-15 ℃的超阈值样本中,数据成串出现(发生时间连续)的频率分别为65%和77%.
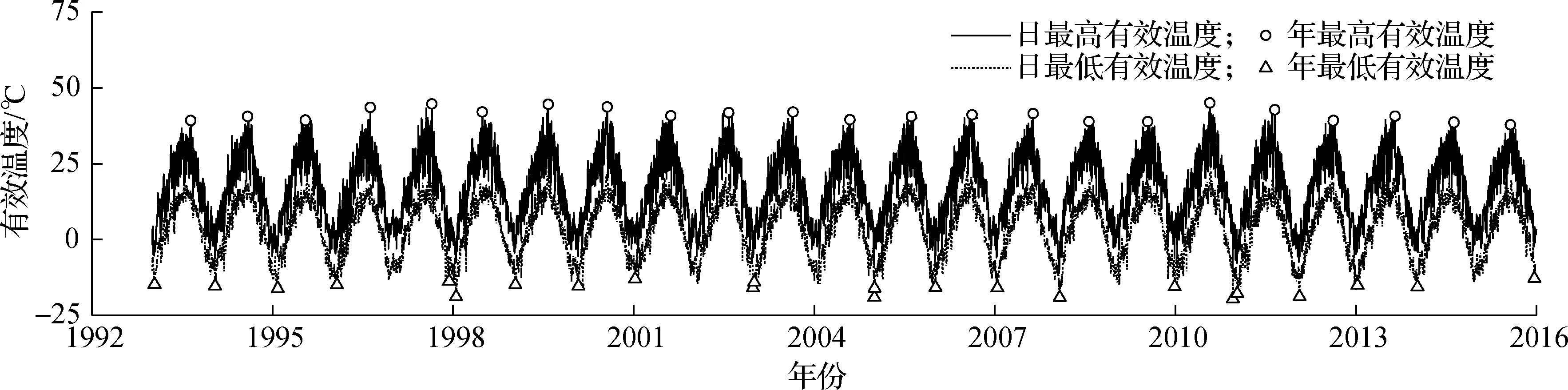
图8 有限元计算有效温度时程
取最高和最低有效温度年极大值,按GEVD分布拟合,样本量均为23,均服从极值Ⅲ型分布,分布参数(k,μ,σ)分别为(-0.128 8,40.289 4,1.842 8)和(-0.142 3,15.246 2,1.716 2),均通过了显著水平为0.05的Pearsonχ2检验.
最高和最低极值温度最接近平均值的阈值分别为40.00和15.00 ℃,超阈值数据按GPD分布拟合,样本量分别为57和60,均服从帕累托Ⅲ型分布,分布参数(k,μ,σ)分别为(-0.436 6,40.00,2.533 3)和(-0.066 5,15.00,1.368 6),均通过了显著水平为0.05的Pearsonχ2检验.
表4给出了基于长期数值模拟数据计算的最高和最低有效温度代表值.模拟计算23 a的最高和最低有效温度分别为45.04和-19.58 ℃.由表可知区组模型推算结果略大于超阈值模型,20 a重现期对应的代表值与23 a模拟极值相近,从而证明了计算结果的合理性.
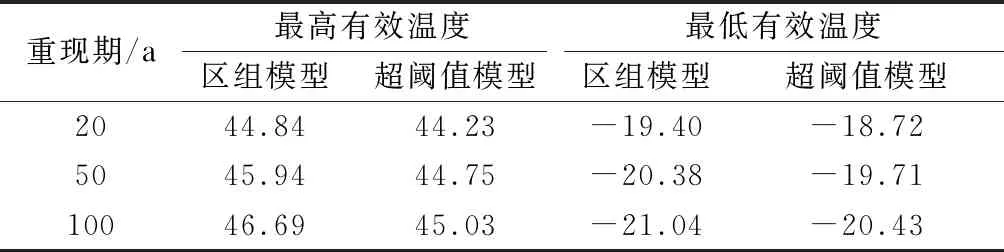
表4 基于长期数值模拟计算的有效温度代表值 ℃
5.3 基于气象相关性公式的计算
将历史气象数据代入拟合的气象相关性公式,得到日最高和最低有效温度时程.每年的最高和最低有效温度分别为37.27~44.94 ℃和-12.50~-19.39 ℃.高于40 ℃和低于-15 ℃的超阈值样本中,数据成串出现的频率分别为87%和82%.
取最高和最低有效温度年极大值按GEVD分布拟合,样本量均为23,分别服从极值Ⅱ型和Ⅲ型分布,分布参数(k,μ,σ)分别为(0.080 5,38.911 3,1.346 3)和(-0.228 4,15.297 3,1.809 0),均通过了显著水平为0.05的Pearsonχ2检验.
最高和最低极值温度最接近平均值的阈值分别为40.00和15.00 ℃,超阈值数据按GPD分布拟合,样本量分别为31和65,均服从帕累托Ⅲ型分布,分布参数(k,μ,σ)分别为(-0.473 9,40.00,2.706 5)和(-0.155 4,15.00,1.463 8),均通过了显著水平为0.05的Pearsonχ2检验.
表5给出了基于气象相关性公式计算数据推算的最高和最低有效温度代表值.公式计算23 a的最高和最低有效温度分别为44.94和-19.39 ℃.由表可知,区组模型推算结果略大于超阈值模型,20 a重现期对应的有效温度代表值与23 a公式计算的有效温度极值相近.
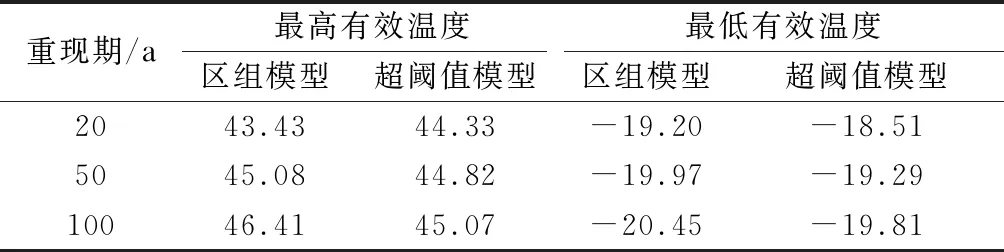
表5 基于气象相关性公式计算的有效温度代表值 ℃
6 结果讨论
图9给出了不同方法推算的组合梁有效温度代表值.由图可知,与其他方法推算结果相比,基于试验测试数据推算的最高有效温度在重现期较短时偏大,在重现期较长时偏小.究其原因在于:① 实测样本较少,导致推算结果偏小;② 受热浪和寒潮影响,因素分离法可能高估了随机部分的极差,使拟合分布产生长尾,导致推算结果偏大(见图10).基于试验测试数据推算的最低有效温度明显偏小,这是因为仪器故障导致缺少冬季的低温数据,桥梁温度试验易发生数据缺失或失真的情况,降低了统计分析的准确性.

(a) 最高有效温度
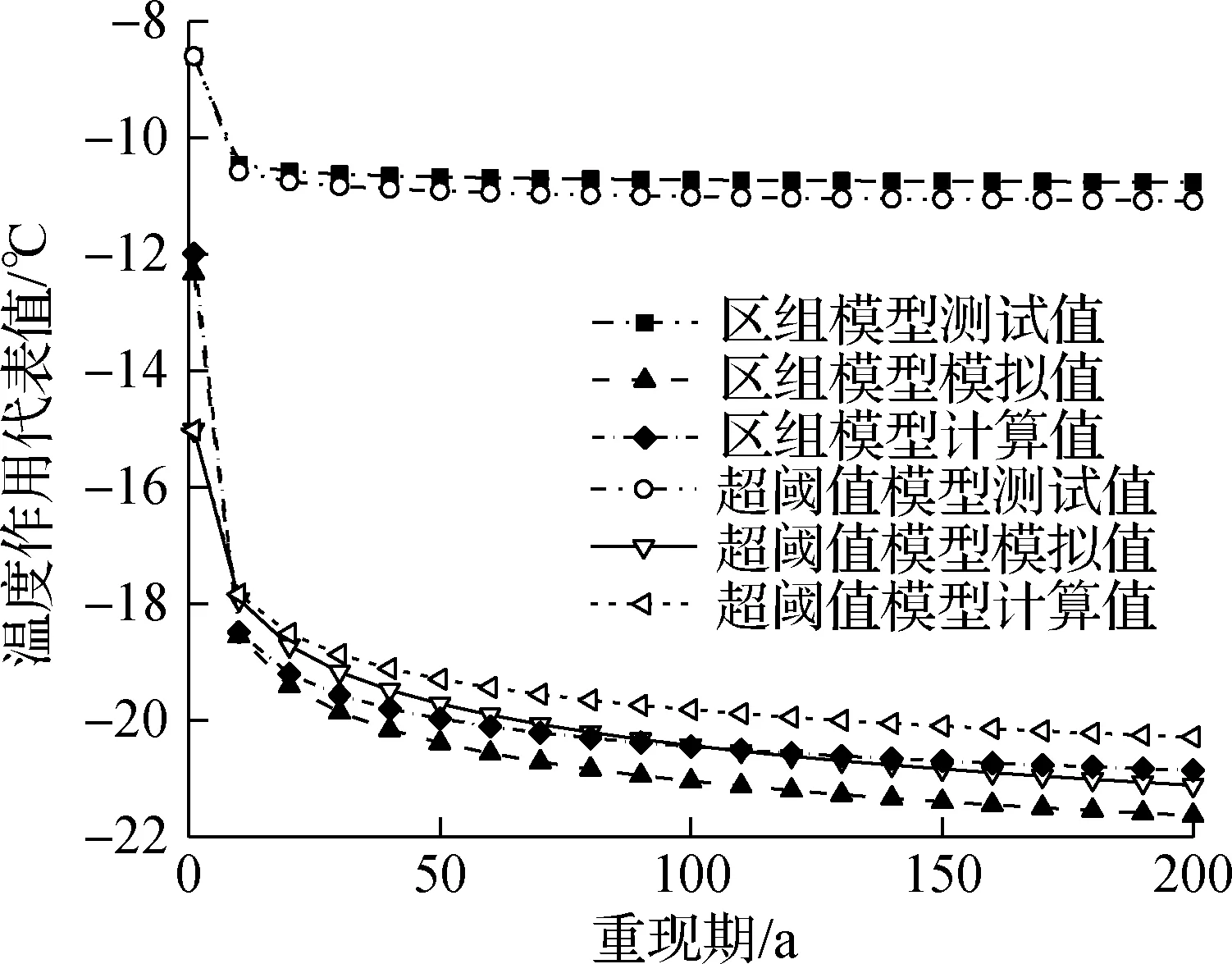
(b) 最低有效温度
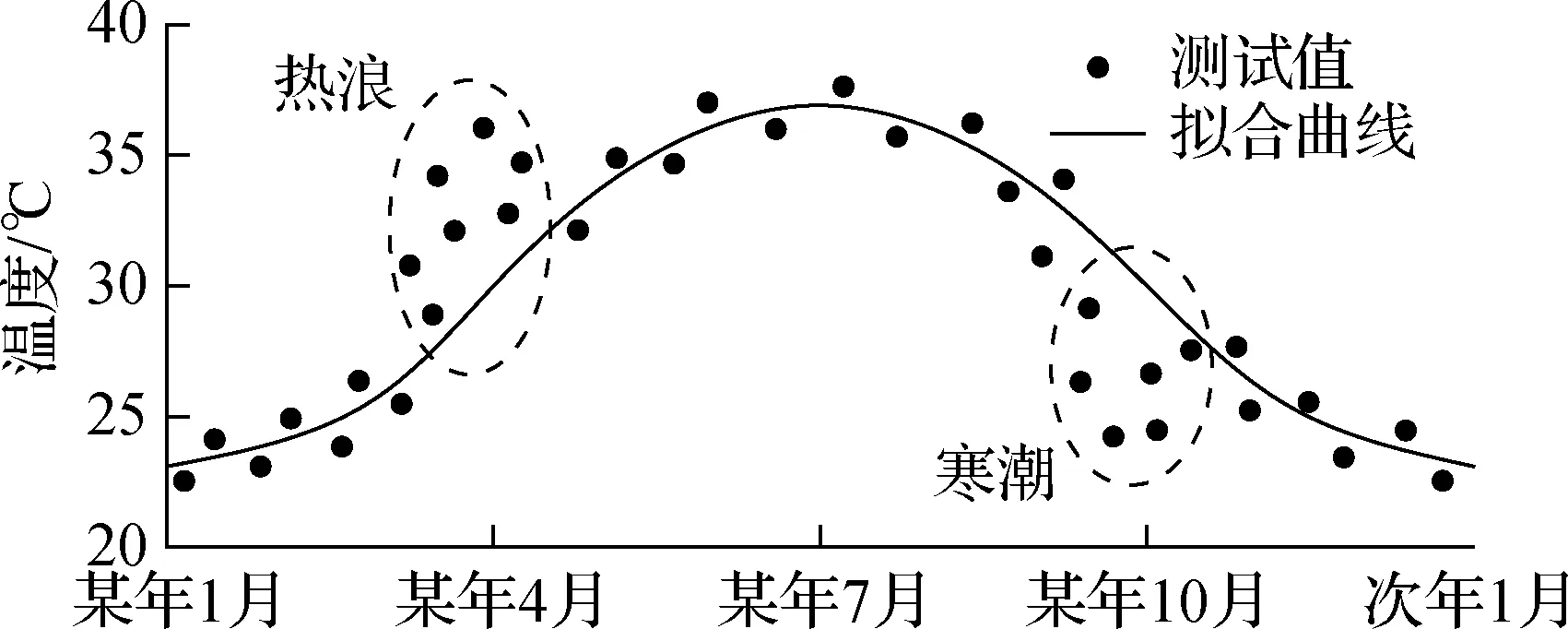
图10 因素分离法误差分析
1.25 a实测的最高和最低有效温度分别为40.99 和-8.91 ℃,与23 a数值模拟和公式计算的最高和最低有效温度相近,取平均值分别为44.99和19.49 ℃.由图9可知,基于长期数值模拟数据推算的有效温度代表值与实测和计算温度极值均较接近,准确性较高,适用性更强.气象相关性公式计算的最高有效温度服从极值Ⅱ型分布,其尾部下降最慢,推算结果比实测和计算温度极值小.基于气象相关性公式推算的最低有效温度与基于长期数值模拟推算结果以及计算温度极值相近.造成最高和最低有效温度推算结果差异的原因是:组合梁日最低有效温度主要受气温影响,气象相关性公式精度较高;而日最高有效温度受气温、辐射、阴影遮挡等多因素影响,基于1.25 a实测数据建立的气象相关性公式,在更长时间尺度上的准确性不够高.对于最高有效温度、温度梯度等影响因素较复杂的温度作用,难以建立起较准确的气象相关性公式,统计分析误差也较大.
在选用合适的区组间隔下,区组模型推算的组合梁有效温度代表值与实测和计算温度极值吻合较好,不同重现期对应的代表值区别更明显,具有更高的准确性和合理性.采用超阈值模型推算的组合梁最高和最低有效温度分别较区组模型小约2和1 ℃.超阈值模型主要关注尾部的极值数据,而桥梁温度作用极值成串出现的概率较高,导致对概率分布的估计不够准确,需要采用一定的方法除串.
按照《公路桥涵设计通用规范》(JTG D60—2015)对混凝土桥面板钢桥有效温度的规定,试验地区组合梁最高和最低有效温度分别为39和-32 ℃[5].本文基于长期数值模拟数据,采用区组模型推算的100 a重现期对应的组合梁最高和最低有效温度代表值分别为46.69和-21.04 ℃,分别较规范取值高7.69和10.96 ℃.现行规范对桥梁的温度作用取值,气候分区范围过大且概率意义不明确,可能与实际有较大偏差,需要进一步开展细化温度分区或绘制等温线图等研究工作.
7 结论
1) 相比于短期试验测试,数值模拟和气象相关性公式计算可以利用历史气象数据,得到更丰富的桥梁温度作用样本,统计分析推算的温度作用代表值更为准确.气象相关性公式对于影响因素较复杂的温度作用准确性不够高,而数值模拟的准确性更高,适用性更强.若气象站点与桥址相距较远,如何衍生得到桥址处的气象数据有待研究.
2) 选择合适的区组间隔,降低区组极值间的相关性,可以提高区组模型统计分析的准确性,推荐采用区组模型来推算桥梁温度作用代表值.桥梁温度作用极值成串出现的概率较高,较强的相关性会降低超阈值模型推算结果的准确性,采用超阈值模型进行桥梁温度作用的极值统计时,需要采用一定的方法除串.
3) 采用因素分离法选择函数拟合桥梁温度作用的规律性变化部分时,需要关注短时热浪和寒潮引起的波动,避免高估随机部分的离散程度,导致统计分析推算代表值偏大.
4) 试验地区钢板组合梁100 a重现期对应的最高有效温度为46.69 ℃,较规范值高7.69 ℃,最低有效温度为-21.04 ℃,较规范值高10.96 ℃.规范未明确温度作用取值的超越概率,且分区范围较大,其对温度作用的规定可能不符合一些地区的实际,有必要开展细化温度分区或绘制等温线图等研究工作.
——平衡不完全区组设计定量资料一元方差分析

