钙质砂颗粒形状及破碎特性试验研究

王 瑞，郭聚坤, ，尹 斌，雷胜友，魏道凯, 3

(1.长安大学 公路学院，陕西 西安 710064; 2.山东交通职业学院 公路与建筑系，山东 潍坊 261206; 3.日喀则市交通运输局工程项目管理中心，西藏 日喀则 857021)

钙质砂在我国南海海域广泛存在，具有多孔隙、形状不规则、易破碎、内摩擦角大等特点[1-2]。众多学者在钙质砂与结构物相互作用力学特性[3-5]、剪切破碎力学特性[6-7]等方面做了大量研究。

钙质砂单颗粒的强度、破碎等力学特性是研究钙质砂宏观力学机制的基础。蒋明镜等[8]将钙质砂单颗粒力—位移曲线分为 “硬化”型、“软化”型与“平坦”型3种类型，发现单颗粒强度与粒径成反比。吕亚茹等[9]通过扫描电镜和X-CT试验，对圆形、枝状和片状3种钙质砂单颗粒的表观和内部结构特征进行研究，得到了钙质砂颗粒的弹性模量、屈服强度和破碎强度，提出了颗粒屈服与破碎应力—应变的指数分布规律。王磊等[10]实现了单颗粒破碎过程的力学加载与声发射监测的同步采集，发现不同粒径钙质砂颗粒的等候时间分布及余震序列分布均满足良好的幂律关系。Xiao等[11]研究发现脆性材料破碎具有离散性，指出颗粒尺寸不同引起材料宏观物理力学特性有所差异，钙质砂的颗粒尺寸效应可以通过Weibull分布进行描述[12]。单颗粒的分形维数D[13]可以预测相同材料的力学性能[14]。徐永福和林飞[15]根据提出的抗张强度公式估算了颗粒在给定压力下的破碎机率。

以0.5～1.0 mm和1.0～2.0 mm粒径范围内的钙质砂颗粒为研究对象，开展了颗粒形状分类统计与块状颗粒的单颗粒破碎试验，根据颗粒的力—位移关系曲线确定了第一次颗粒破碎力、颗粒破碎峰值力及颗粒完全破碎力，对单颗粒强度、颗粒破碎能量与平均粒径的关系进行了分析。成果对钙质砂的强度、变形和破碎的研究具有重要意义。

1 钙质砂单颗粒形状分析

通过四分法随机选取0.5～1.0 mm和1.0～2.0 mm范围内钙质砂颗粒，颗粒数分别为92和83，颗粒选取与编号如图1所示。

图1 颗粒选取与编号

陈海洋等[16]指出钙质砂的块状、纺锤状颗粒的长宽比在1～3之间，片状及枝状颗粒的长宽比均大于3。采用电子游标卡尺测量了各颗粒在x、y及z三个相互垂直方向上的长度，规定最大值为l1，中间值为l2，最小值为l3，根据l1/l2和l1/l3的数值关系，将颗粒形状分成块状、较片状、片状、小长条状、扁长条状和细长条状共6类，如图2所示。

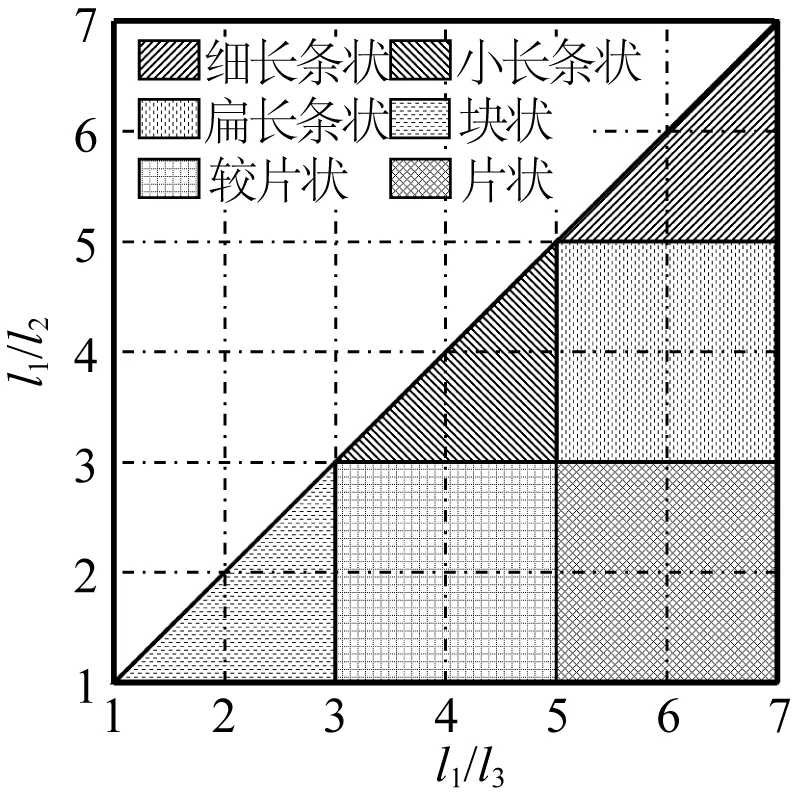
图2 颗粒形状划分

不同形状颗粒统计如表1所示，分析发现0.5～1.0 mm范围的块状颗粒所占比例为95.7%，没有扁长条状和细长条状颗粒，其余形状所占比例为4.3%，1.0～2.0 mm范围的块状颗粒所占比例为85.5%，没有扁长条状颗粒，其余形状所占比例为14.5%，可见1.0～2.0 mm范围内的钙质砂颗粒形状更不规则。

表1 不同形状颗粒数量统计

分别将l1/l2、l1/l3和l2/l3的所有数值划分为10组，由式(1)计算出加权平均组中值。

(1)

式中：ni为各组中值，ki为各组中值对应频数，k为总频数。加权平均组中值如表2所示，可以看出0.5～1.0 mm范围的l1/l2、l1/l3和l2/l3较1.0～2.0 mm范围的更小，说明后者颗粒形状的不规则程度更大。绘制(频率/组距)m与组中值n间的柱状关系图，如图3所示。研究发现m与n的关系可以用高斯分布函数General model Gauss1进行描述，见式(2)，相关系数R2均大于0.91，拟合效果较好。

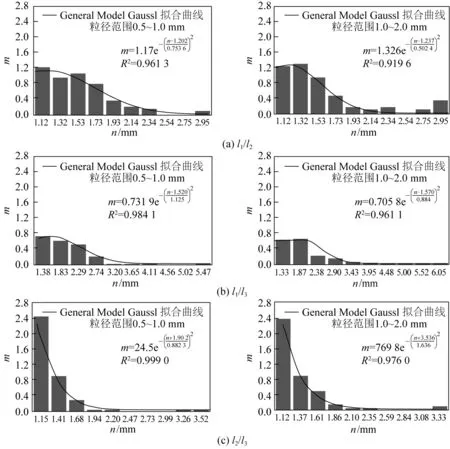
图3 (频率/组距)m与组中值n的关系

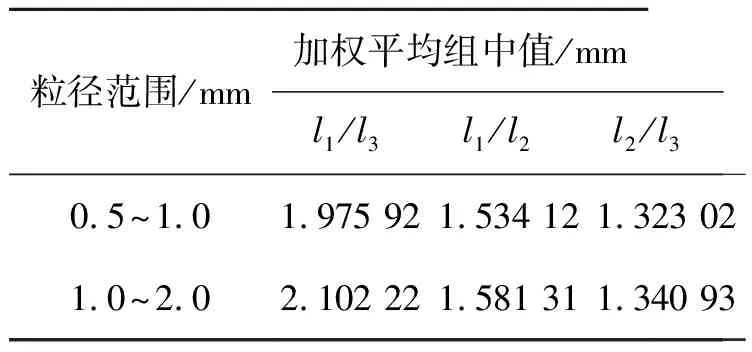
表2 加权平均组中值

(2)

其中，a、b和c为拟合系数。

2 钙质砂单颗粒强度

2.1 力—位移关系

通过万能拉力试验机对随机选取到的颗粒开展了单颗粒破碎试验，试验设备如图4所示，该设备可提供最大力值为500 N，传感器精度为0.3%，试验速率为0.08 mm/min。对于采集到的颗粒力—位移关系曲线，0.5～1.0 mm粒径范围的颗粒最大位移取至0.8 mm，1.0～2.0 mm粒径范围的颗粒最大位移取至1.5 mm。

图4 万能拉力试验机示意

块状颗粒的力—位移曲线如图5所示，颗粒破碎过程分为以下5种情况：

1)如图5(a)所示，对于情况Ⅰ，以0.5～1.0 mm的45号颗粒和1.0～2.0 mm的33号颗粒为例，在试验初始阶段，随着法向力的增加，力与位移呈线性增长关系，此阶段为弹性阶段，直至位移增大至一定数值后，力值迅速减小，颗粒发生第一次破碎，将发生第一次破碎时的力值称为第一次颗粒破碎力，在图中用★表示。第一次颗粒破碎力减小至一定数值后力值又逐渐增加，可见发生第一次破碎后的颗粒仍能继续承受上部荷载，这里把这个阶段称为应变硬化阶段，此阶段力值的增加表现为迅速增大或缓慢增加甚至出现相对平稳段(屈服)，当力值增加到一定数值后又会出现力值的突然减小，说明颗粒发生了第二次破碎，此后力值又会出现增加和突然减小的反复变化，此现象表现为颗粒的多次破碎，在上述多次破碎中出现过的力值最大值称之为颗粒破碎峰值力，在图中用●表示。最后一次发生力值突然减小即颗粒最后一次破碎时的力称之为颗粒完全破碎力，在图中用▲表示。在情况Ⅰ中，颗粒破碎峰值力和颗粒完全破碎力出现在同一点，且大于第一次颗粒破碎力。在颗粒发生最后一次破碎后力值会随着位移的增大一直增加，表现为曲线一直上升，此过程颗粒已被完全压碎至粉末。从图5(a)中可以看出，粒径较大的33号颗粒的3个力值要远大于粒径较小的45号颗粒，且33号颗粒力—位移曲线的波动次数和幅度要明显大于45号颗粒。

2)如图5(b)所示，对于情况Ⅱ，以0.5～1.0 mm的28号颗粒和1.0～2.0 mm的11号颗粒为例，在整个试验过程中，颗粒发生了多次破碎，但与情况Ⅰ不同的是，颗粒第一次破碎力、破碎峰值力和完全破碎力均出现在不同位移处，可以看出粒径较大的11号颗粒除第一次破碎力较小外，破碎峰值力和完全破碎力远大于粒径较小的28号颗粒。

3)如图5(c)所示，情况Ⅲ仅出现在0.5～1.0 mm的颗粒中，以32号颗粒为例，试验过程中颗粒仅发生了一次破碎，因此，颗粒第一次破碎力、破碎峰值力和完全破碎力出现在相同位移处，为同一数值。

4)如图5(d)所示，情况Ⅳ也仅出现在0.5～1.0 mm的颗粒中，以27号颗粒为例，试验过程中颗粒发生了多次破碎，颗粒第一次破碎力和破碎峰值力为同一数值，比颗粒完全破碎力要大。

5)如图5(e)所示，情况Ⅴ也仅出现在0.5～1.0 mm的颗粒中，以13号颗粒为例，在整个试验中，力随位移的增大一直增加，未出现力值突然减小的现象，即颗粒没有发生过断裂现象，而是从试验一开始就进入了压碎至粉末的过程，因此，在情况Ⅴ中未出现前述3个力值。

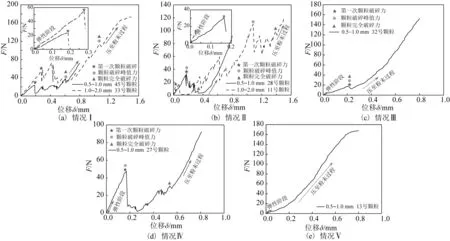
图5 块状颗粒力—位移关系曲线

对上述分析的5种情况次数进行了统计，对于0.5～1.0 mm粒径范围的颗粒，情况Ⅰ和情况Ⅱ出现的次数最多，分别为31次和38次，其余情况出现了19次，对于粒径1.0～2.0 mm范围的颗粒，仅出现情况Ⅰ和情况Ⅱ，次数分别为41次和30次。

块状以外其他形状颗粒的力—位移关系曲线如图6所示，0.5～1.0 mm粒径范围以10号、72号和87号颗粒为例，1.0～2.0 mm粒径范围以30号、51号、54号和5号颗粒为例。可以看出：1)0.5～1.0 mm粒径范围的10号片状颗粒、72号较片状颗粒和87号小长条状颗粒的力—位移曲线分别符合情况Ⅴ、Ⅴ和Ⅱ；2)1.0～2.0 mm粒径范围的5号小长条状颗粒、30号较片状颗粒、51号片状颗粒和54号片状颗粒的力—位移曲线分别符合情况Ⅰ、Ⅰ、Ⅱ和Ⅴ。

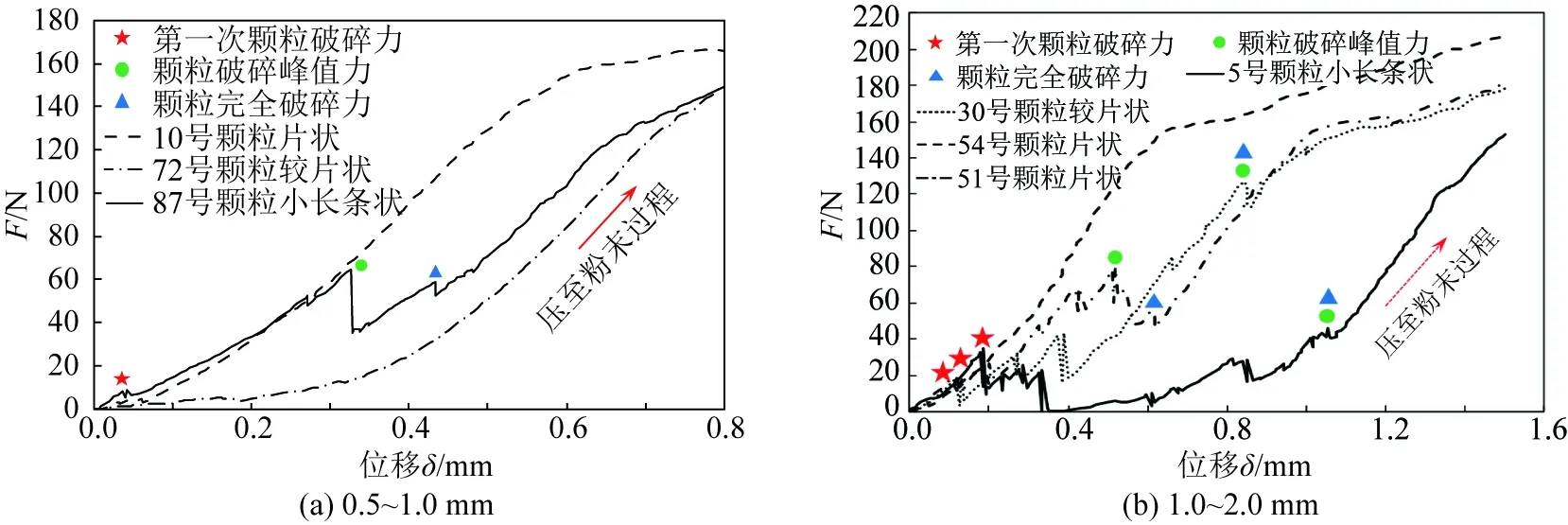
图6 非块状颗粒力—位移曲线

从上述分析可知，块状颗粒数量所占比例最多，是决定钙质砂强度的主要颗粒，因此，单颗粒强度和单颗粒破碎能量的研究以块状颗粒为研究对象。

2.2 单颗粒强度与平均粒径关系

单颗粒强度是指在整个试验过程中，颗粒单位面积上所能承受最大压力的能力。采用式(3)描述单颗粒在两个平行加载板之间的应力状态：

(3)

其中，σf为单颗粒强度，Ff为峰值破碎力，d为颗粒平均粒径，即l1、l2及l3的平均值。鉴于对钙质砂单颗粒力—位移关系5种情况的分析，对0.5～1.0 mm粒径范围81个块状颗粒和1.0～2.0 mm粒径范围71个块状颗粒的单颗粒强度进行了计算，统计结果如图7所示。可以看出不同粒径范围内的钙质砂，单颗粒强度具有离散性，0.5～1.0 mm粒径范围的钙质砂单颗粒强度主要集中在20～60 kPa范围内，单颗粒最大强度约97 kPa，单颗粒最小强度约8 kPa，1.0～2.0 mm粒径范围的钙质砂单颗粒强度主要集中在10～40 kPa范围内，单颗粒最大强度约72 kPa，单颗粒最小强度约4 kPa，上述数据表明平均粒径较小的钙质砂单颗粒强度要更大一些。Xu[17]研究发现单颗粒强度与平均粒径之间的关系为：

图7 σf与d关系

(4)

用对数关系表示为：

(5)

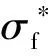
图8 lnσf与lnd关系

2.3 单颗粒破碎能量

峰值位移δf与颗粒平均粒径d主要表现为线性关系[19]，对文中试验数据进行线性拟合，如图9所示，拟合公式为：

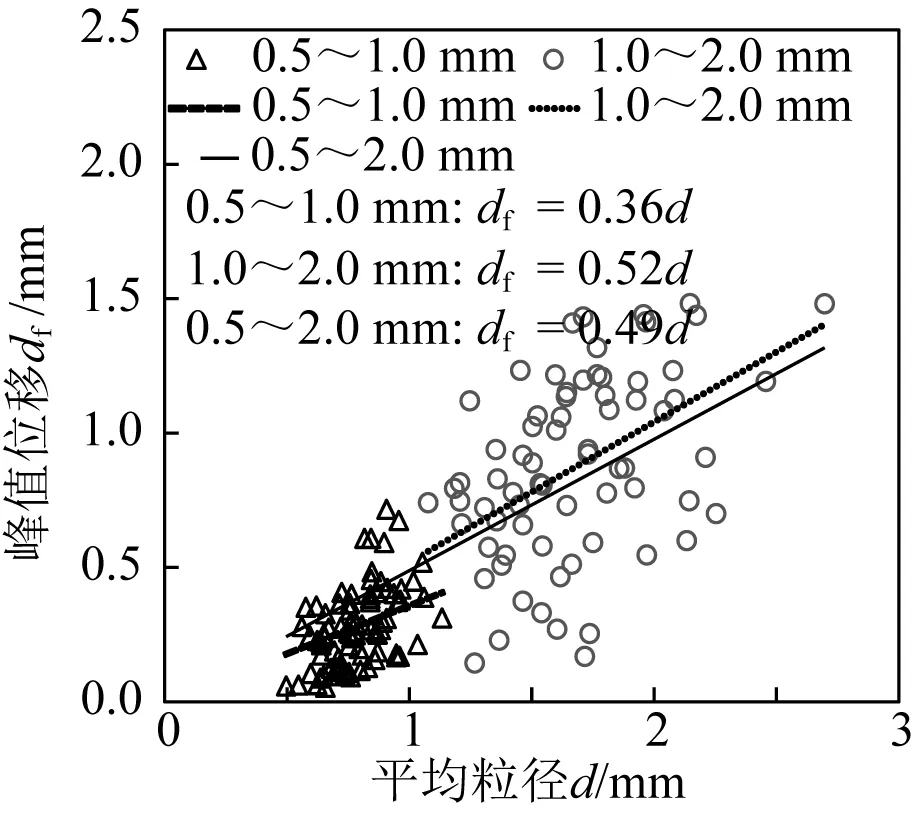
图9 δf与d关系

δf=kd

(6)

可以看出k值均大于0，颗粒峰值位移随平均粒径的增大而增加，二者呈正相关。

文中研究的单颗粒破碎能量是指单颗粒达到峰值破碎力时所做的功，公式为：

(7)

如前所述，钙质砂单颗粒力—位移关系曲线波动幅度较大，难于通过函数关系式进行描述。针对此问题，王益栋等[19]在研究大理石岩破碎时破碎功取为峰值力与峰值位移乘积的一半，通过观察所有颗粒力—位移关系曲线，并经过不断试算，0.5～1.0 mm粒径范围和1.0～2.0 mm粒径范围钙质砂单颗粒破碎能量采用式(8)进行计算，单颗粒破碎能量计算示意如图10所示。

图10 破碎能量计算示意

(8)

通过式(8)计算并统计出单颗粒破碎能量Wf与平均粒径d的关系如图11所示，可以看出1.0～2.0 mm粒径范围的单颗粒破碎能量较0.5～1.0 mm粒径范围的要更大，前者的数据离散性也更显著，0.5～1.0 mm粒径范围的单颗粒破碎能量集中在0.19～16.23 mJ范围内，1.0～2.0 mm粒径范围的单颗粒破碎能量集中在1.02～54.83 mJ范围内。上述数据表明平均粒径较大的单颗粒破碎能量要更大一些，这与单颗粒强度与平均粒径关系正好相反。结合式(4)、式(6)和式(8)计算得出单颗粒破碎能量与平均粒径关系为：

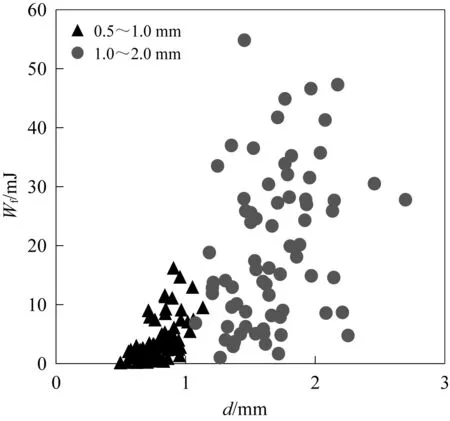
图11 Wf与d的关系

Wf=pdD∝dD

(9)

式中：p为拟合系数。式(9)用对数关系表示为：

lnWf=lnp+Dlnd

(10)

对式(10)进行计算并统计得出lnWf和lnd的关系，如图12所示。lnWf和lnd的关系采用线性函数进行表示，拟合得到0.5～1.0 mm、1.0～2.0 mm和0.5～2.0 mm粒径范围的分形维数D分别为2.91、1.96和2.46，与图8得到的分形维数D随粒径的变化规律基本一致。

图12 lnWf和lnd的关系

3 结 语

以钙质砂颗粒为研究对象，开展了颗粒形状分类统计与单颗粒破碎试验，研究了颗粒的力—位移关系曲线、单颗粒强度和单颗粒破碎能量，得出了如下结论：

1)0.5～1.0 mm和1.0～2.0 mm粒径范围的块状颗粒所占比例分别为95.7%和85.5%，后者的钙质砂颗粒形状更不规则。(频率/组距)m与组中值n间的柱状关系图可以用高斯分布函数进行描述，拟合效果较好。

2)根据块状颗粒力—位移关系曲线中第一次颗粒破碎力、颗粒破碎峰值力和颗粒完全破碎力出现位置的不同，将颗粒的破碎过程分成5种情况。以颗粒发生多次破碎为特征的情况Ⅰ(第一次颗粒破碎力为单独点，颗粒破碎峰值力和颗粒完全破碎力相同)和情况Ⅱ(3种力出现在不同位移处)出现次数最多，其余情况仅在0.5～1.0 mm粒径范围出现。

3)单颗粒强度分布具有离散性，随平均粒径的增加呈减小趋势，1.0～2.0 mm粒径范围的分形维数较0.5～1.0 mm的更小，说明粒径较大的钙质砂颗粒更容易破碎。

4)颗粒峰值位移与平均粒径呈正相关，简化了钙质砂单颗粒破碎能量计算公式，1.0～2.0 mm粒径范围的单颗粒破碎能量较0.5～1.0 mm的更大，根据破碎能量统计得到的分形维数随粒径的增大而减小。