多边形筒型基础海上建造过程中移位及起浮技术研究

练继建，刘畅博，郭耀华，董霄峰，刘维斌，张 斌

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.天津大学 建筑工程学院，天津 300072; 3.南方海上风电联合开发有限公司，广东 珠海 510000)

随着近海资源的不断开发，海上风电逐渐向深远海、大容量、低成本发展[1]。我国海域大部分为软黏土与粉砂地质，地质条件较差，承载能力低[2]，而筒型基础由于其施工操作简单，且可与地基协同抵抗环境荷载，有良好的承载性能与抗滑抗倾覆能力，越来越受到关注。为进一步降低海上风电建设成本，提高筒型基础浮运、安装及服役过程的安全性及承载性能，筒型基础将由钢筒向钢混组合筒发展[3]，结构质量大大增加。目前，筒型基础均在近岸码头预制，然后吊装入水[4]，然而钢混组合筒型基础对吊装设备提出了更高的要求，导致施工成本增加。筒型基础由于内部为分舱结构，其自身具有较好的浮稳性，可以实现水中自浮、湿拖等操作[5]。因此，为充分发挥筒型基础水中自浮特性，将筒型基础陆上预制变为海上建造。筒型基础的海上建造首先在自升式预制平台上进行筒裙建造，然后将筒裙移位到海底的预制沉垫上进行筒顶以上结构的建造，最后将建造好的筒型基础自浮出运与浮运安装船对接。这种海上建造方式不仅可以实现多个筒型基础的同步快速预制安装，提升施工效率，而且可实现预制设备在不同海域的重复使用，降低建造成本。但海上建造过程存在敞口筒裙无法自浮移位与筒型基础起浮稳性不足的问题。工程中常增设助浮结构来提供回复力矩使气浮体稳定地漂浮[6]，故针对筒型基础设计配套的助浮浮箱。

早在20世纪80年代，国内的专家就开始研发多用途浮箱并针对该钢浮箱的设计、制造与应用进行了试验与理论研究[7]。丁宁等[8]研究了用于军事渡河与栈桥通道的浮箱，解决了快速、稳定、安全搭建临时栈桥的难题。杨少宏[9]分析了浮箱拼成的浮驳平台在满载及空载工况下的稳定性。陈宝林等[10]阐述了浮箱架设的临时作业平台的力学分析模型与基本方法。郭称龙[11]通过北山特大桥施工工程实例，讲述了深水中浮箱拼组搅拌平台的设计与应用技术。齐建飞[12]阐述了用于船闸防撞浮箱的施工过程,并进行了相应校核。刘红平[13]针对半潜船设计了可移动式浮箱结构，并进行了强度校核。

目前，现有的浮箱结构多集中于船舶设计过程中，针对筒型基础的助浮浮箱还没有过系统研究。因此，基于广东省某海域海上风电项目，建立整体模型，分别研究了敞口筒裙—浮箱、筒型基础—浮箱在水中移位、起浮过程中的运动响应与结构强度，为浮箱在筒型基础海上建造的实际运用提供科学支撑。

1 助浮浮箱结构设计

1.1 浮箱结构方案

以广东省某海域海上风电工程为实例，提出了一种在六边形钢混组合筒型基础海上建造中配套使用的浮箱，将浮箱布置在筒型基础的六边，以提供所需浮力与回复力臂，使基础在预制及浮运中保持稳定的姿态，完成筒型基础的海上建造。图1为六边形筒型基础助浮浮箱结构模型。

图1 六边形筒型基础助浮浮箱结构模型

浮箱尺寸为15.0 m×2.5 m×12.0 m(长×宽×高)，内设梁—柱式格构，浮箱高度5.2 m处设置水平分舱板将浮箱分为上下两个可变压载舱，通过调节自身压载量，灵活控制整个结构的起浮与沉放过程。六边形筒型基础与浮箱之间，通过高强缆绳连接浮箱上的垂直吊点与基础底部吊点以实现筒型基础与浮箱结构一体化。此外，采用高强缆绳连接两两浮箱之间的水平吊点，既约束了浮箱的自由度，又提高了结构整体稳定性。为保证浮箱吊点处强度满足要求，对吊点局部结构进行优化加强，图1(b)为浮箱吊点局部结构优化后的示意。图2为筒型基础浮箱现场图。浮箱的主要参数如表1所示。

图2 六边形筒型基础助浮浮箱现场照片

表1 6个浮箱主要尺寸参数

1.2 敞口筒裙—浮箱水中移位方案

敞口筒裙未形成封闭的内舱空间，自身没有足够的浮力与回复力臂，不具备浮稳性，因此不能稳定地漂浮在水中。而中空的箱型浮箱能给筒裙提供足够的外部浮力，二者的组合结构具有足够的自浮稳性，能够顺利完成从预制平台到沉垫的移位。筒裙的主要几何参数如表2所示。

表2 筒裙主要尺寸参数

海上建造过程中浮箱助浮敞口筒裙移位过程简要步骤为：

1)筒型基础下部筒裙在预制平台上进行筒裙钢模板架设与混凝土浇筑。

2)将漂浮在水面的浮箱一个个拖至现场对应位置，完成水平绑扎。

3)打开浮箱阀门自流注水，使其缓慢下沉，在浮箱坐底后关闭阀门，并与筒裙完成绑扎。

4)浮箱打气排水，带敞口筒裙起浮，与预制平台分离。

5)卷扬机牵引，使敞口筒裙—浮箱移位至沉垫；浮箱打开阀门注水，使整体坐底于沉垫。

浮箱助浮筒裙移位过程如图3所示。

图3 浮箱助浮筒裙移位流程

1.3 筒型基础—浮箱水中起浮方案

与传统的实浮体结构不同，筒型基础底部不封闭，依靠舱内充气排水产生压差来平衡自身重力，是能够实现自浮的气浮体结构。但由于钢混组合筒型基础自重大，再加上弧形过渡段后，重心太高，稳性不够，因此需要采取工程措施增加其浮稳性。筒型基础的主要几何参数如表3所示。

表3 筒型基础主要尺寸参数

气浮筒型基础结构的重心与稳心之间的距离为稳心高度GM，对筒型基础在不同吃水深度的完整稳性进行理论计算，如表4所示。由表4可知，筒型基础完整稳性较差，吃水深度为13 m才具有回复力臂。而筒型基础建造所处海域水深较浅，最低潮位时水深8.1 m，最高潮位时水深11.5 m，筒型基础在该海域水深条件下不具有自浮稳性。因此，筒型基础起浮过程采用浮箱来改善结构稳性，浮箱布置在筒裙外壁，大大增加了基础的回复力臂，使基础在整个起浮过程的各个吃水下均满足自浮稳性，达到助稳效果。

表4 筒型基础不同外吃水深度完整稳性计算结果 Tab.4 Static stability of bucket foundation with different draft depths 单位:m

浮箱助浮筒型基础起浮流程如图4所示，其起浮过程简要步骤为：

图4 浮箱助浮筒型基础起浮流程

1)筒型基础整体浇筑完毕。

2)浮箱排水，带筒型基础起浮，与沉垫/预制平台分离。浮箱—筒型基础起浮安全距离≥1 m。

3)至此，整个海上建造过程完成，筒型基础—浮箱与浮运安装船对接，如图5所示。

图5 筒型基础—浮箱与浮运船对接示意

2 敞口筒裙浮箱移位过程结构浮稳性及受力分析

在敞口筒裙—浮箱移位过程中整体结构有两种状态：漂浮状态与坐底状态。该过程一方面需要保证敞口筒裙—浮箱结构在漂浮状态具有足够的稳性和良好的运动性能，另一方面需要保证浮箱与筒裙结构在漂浮状态与坐底状态下的结构强度均满足要求。

2.1 漂浮状态整体运动响应及强度校核

2.1.1 完整稳性及运动响应分析

为了研究敞口筒裙—浮箱在移位过程中的稳性问题，采用有限元软件SESAM中的HydroD稳性分析模块对结构进行稳性计算与分析，得到敞口筒裙—浮箱在不同吃水深度下的完整稳性曲线，如图6所示。

图6 敞口筒裙浮箱完整稳性曲线

由图6可知，在不同吃水下敞口筒裙浮箱的回复力臂均大于风倾力臂。由于目前还未有针对筒型基础的稳性判断标准，参考中国船级社《海上移动平台入级规范》[14]中对各类型海洋移动平台中最严格的稳性判断标准，对敞口筒裙—浮箱进行完整稳性校核，规范要求：1)自由液面修正后初稳性高不少于0.15 m；2)对于面积比，要求复原力矩曲线至第二交点或进水角(取小者)以下的面积至少应比风压倾侧力矩至同一限定角下的面积大40%。其中，根据自存工况最小风速要求，风速选择100 kn(51.5 m/s)；由于筒裙上下均敞口，浮箱为全封闭结构，敞口筒裙—浮箱中不存在进水角，直接选取复原力矩曲线至第二交点以下的面积与风压倾侧力矩至同一限定角下的面积进行面积比计算。表5为敞口筒裙—浮箱在不同吃水下的稳性校核，由表5可知，敞口筒裙—浮箱的初稳性高与面积比K均大于中国船级社要求，且结构具有较大的稳性储备。

表5 敞口筒裙—浮箱稳性校核

为避免发生共振破坏，保证敞口筒裙—浮箱具有良好的运动性能，采用SESAM软件，通过势流边界元方法对敞口筒裙—浮箱进行频域水动力计算，得到不同吃水深度下敞口筒裙—浮箱的垂荡与纵摇运动响应幅值算子(RAO)，如图7和图8所示。

图7 敞口筒裙—浮箱垂荡RAO曲线

图8 敞口筒裙—浮箱纵摇RAO曲线

由图7可知，敞口筒裙—浮箱的垂荡RAO出现两个峰值，第一个峰值较低，对应波浪载荷最大值点[15]，第二个峰值较高，对应固有周期点，随吃水的增加，其垂荡固有周期也增大，吃水深度7 m时峰值响应出现在10 s，吃水深度11.5 m时出现在11 s；垂荡RAO幅值也随吃水深度增加而增大，吃水深度从7 m增加到11.5 m，垂荡运动的最大幅值增幅为44.57%。由图8可以看出，敞口筒裙—浮箱纵摇RAO仅在固有周期出现峰值，随着吃水深度的增加，敞口筒裙—浮箱纵摇固有周期也略微增大，吃水深度7 m时峰值响应出现在6.8 s，吃水深度11.5 m时出现在7.6 s，吃水深度从7 m增加到11.5 m，纵摇运动的最大幅值增幅为7.70%。在实际操作中，应避免在波浪周期与结构固有周期接近的海况下施工，减小共振风险；该结构在11.5 m吃水深度下的运动响应较大，为改善运动性能，应避免在高潮位起浮。

2.1.2 漂浮状态强度校核

采用ABAQUS软件建立敞口筒裙—浮箱数值模型，由于结构六边对称，仅建出一个浮箱进行分析，钢结构中钢板采用S4R壳单元，吊点圆钢采用C3D8R实体单元，屈服强度为355 MPa，弹性模量为2.1×105MPa，泊松比为0.30，密度为7.85×103kg/m3；混凝土采用C3D8R实体单元，弹性模量为3.5×104MPa，泊松比为0.167，密度为2.50×103kg/m3。敞口筒裙—浮箱处于漂浮状态时，筒裙重力由浮箱12个Ⅰ型与12个Ⅱ型垂直吊点承担，同时向浮箱与筒裙间的气囊充气，使每侧水平吊点处的高强缆绳产生5400 kN张力，对漂浮状态整体结构强度进行校核。

为了真实模拟结构在漂浮状态下的受力情况，采用DNV柱稳式平台固定边界条件法[16]，对模型的3个节点进行全约束。参考相关规范[17]，选取荷载安全系数为1.35。高强尼龙缆绳对吊点的拉力以面荷载施加在吊点与缆绳的接触面，其各吊点荷载值见表6，边界及加载情况如图9所示。

表6 敞口筒裙—浮箱漂浮工况荷载情况

图9 敞口筒裙—浮箱有限元模型

在漂浮状态下，敞口筒裙—浮箱整体结构应力云图见图10，各构件的变形及应力汇总于表7。由图10可知，敞口筒裙—浮箱钢结构最大Mises应力为231.9 MPa，位于浮箱水平桁与水平吊点连接点，浮箱整体受力均匀，无应力集中；筒裙受力小，钢结构最大Mises应力为72.7 MPa，位于筒裙与浮箱接触上缘。结构各构件应力计算值均小于许用应力值248 MPa[18]，结构强度满足要求。

图10 漂浮工况敞口筒裙—浮箱结构Mises应力云图

表7 敞口筒裙—浮箱漂浮状态各构件变形及应力结果

2.2 坐底状态强度校核

敞口筒裙—浮箱在坐底状态下，通过对浮箱上下舱分别打气排水，实现结构与预制平台分离。首先对起浮时刻结构的受力情况进行计算。

FFX=ρgV=6ρghFXSFX

(1)

式中：FFX为浮箱产生的浮力；ρ为海水密度；g为重力加速度；V为6个浮箱的排水体积；hFX为浮箱内外液面高度差；SFX为浮箱底面面积。

WTQ+WFX=FFX=6ρghFXSFX

(2)

式中：WTQ为筒裙重力；WFX为浮箱重力。

根据式(2)计算可知，浮箱内外液面高度差为8.2 m时，敞口筒裙—浮箱开始起浮。在敞口筒裙—浮箱坐底状态，首先对浮箱上舱打气排出全部压载水，其次对浮箱下舱打气排出部分压载水，使浮箱转换为漂浮状态。对上、下舱打气排水过程中最不利时刻的整体结构强度进行校核，坐底工况下敞口筒裙—浮箱的荷载情况如表8所示，荷载及边界条件如图11所示。

表8 敞口筒裙—浮箱坐底工况荷载情况 Tab.8 The load situation of open bucket skirt-floating container under bottom-resting conditions 单位:m

图11 敞口筒裙—浮箱坐底工况有限元模型、荷载及边界条件施加

在坐底状态下，敞口筒裙—浮箱上下舱打压整体结构应力云图见图12，各构件变形及应力结果汇总于表9。由图12可知，上舱打压时敞口筒裙—浮箱钢结构最大Mises应力为233.5 MPa，位于浮箱上舱支撑柱处，局部出现应力集中现象；下舱打压时整体的钢结构最大Mises应力为140.2 MPa，位于浮箱分舱板肋骨处，整体结构受力较好。结构各构件应力计算值均小于许用应力值248 MPa[18]，结构强度满足要求。

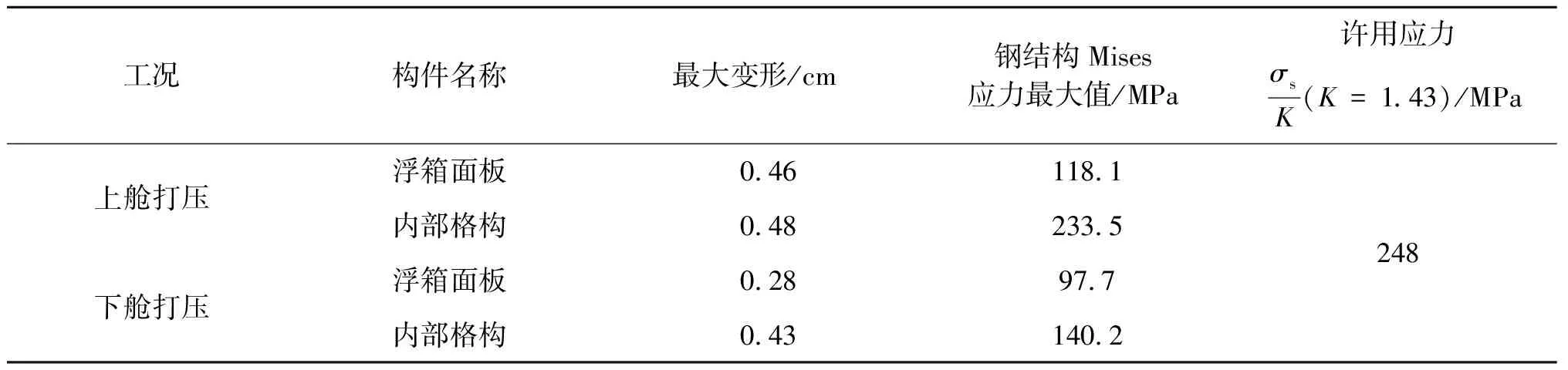
表9 敞口筒裙—浮箱坐底工况各构件变形及应力结果

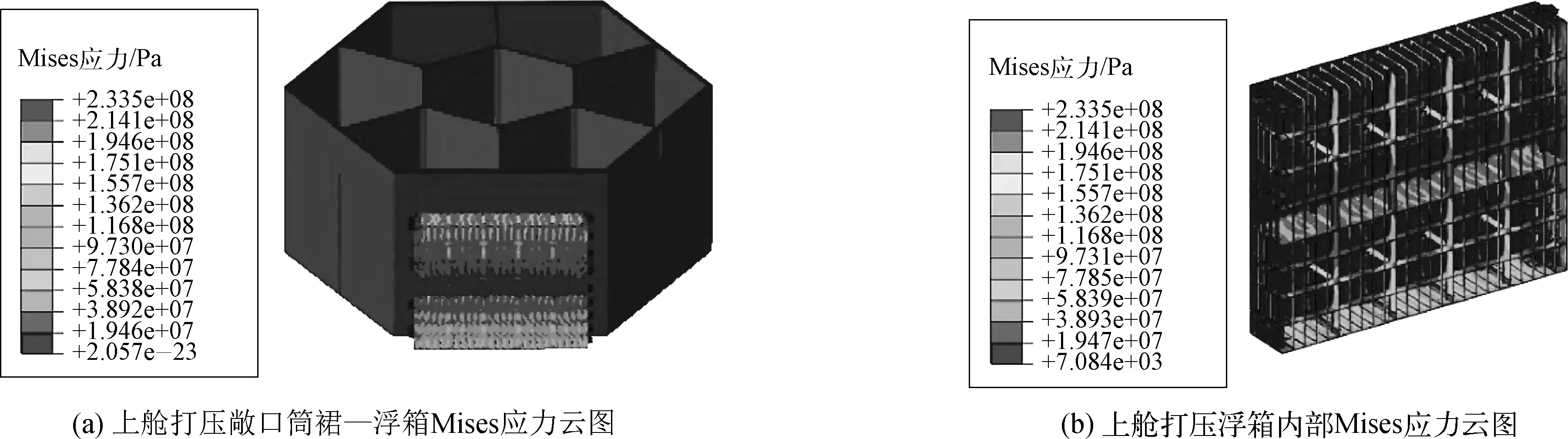
图12 坐底工况敞口筒裙—浮箱结构Mises应力云图

3 筒型基础—浮箱起浮过程结构浮稳性分析

3.1 浮态分析

实浮体的静力平衡条件为重力与浮力相等，而气浮体的静力平衡条件为向上的气压力与重力相等。筒型基础为气浮体，浮箱为实浮体。因此，需对筒型基础内部气压与浮箱自身浮力进行计算，从而分析筒型基础—浮箱的整体浮态。筒型基础内部气压P为：

P=ρghT

(3)

式中：hT为筒型基础内外液面高度差。对整个结构而言，静力平衡公式为：

WT+WFX=PST+FFX=ρghTST+6ρghFXSFX

(4)

式中：WT为筒型基础重力；ST为筒型基础底面面积。由式(4)可知，在结构确定后，筒型基础—浮箱的浮态不仅与浮箱内外液面差有关，还与基础内外液面差有关。因此，为简化施工过程，提高建造效率，应该首先确定浮箱内液面高度，再根据不同吃水深度确定浮箱提供的浮力，最后确定基础内部水头高度。

3.2 稳性及运动响应分析

筒型基础—浮箱是拥有自浮能力的气浮体，当气浮结构倾斜时，如果内部液封高度为0，舱内气体会部分或全部溢出，破坏结构稳性，导致结构倾覆，因此，气浮体首先要确定内部的安全液封高度，并计算结构的破舱倾角φp。以单舱气浮体为例，简化模型如图13所示。

图13 气浮体简化模型

其中，气浮体高度为H，外径为D，倾斜角为φ；气浮体倾斜前后的筒顶距水面的垂直高度分别为Hf1和Hf2，倾斜前后吃水分别是Hd1和Hd2，倾斜前后内外液面的高度差是ΔH1和ΔH2，倾斜前后的安全液封高度为b1和b2。根据图13，列出气浮体倾斜角度φ与安全液封高度的公式为：

(5)

由式(5)可得，在气浮体尺寸一定时，破舱倾角φp能够通过正浮吃水Hd与安全液封高度b来确定。

为保证筒型基础浮箱顺利起浮，在筒型基础—浮箱坐底状态对浮箱内液面进行调整确认：排出6个浮箱全部的上舱水，此时浮箱内液面为5.2 m，后续仅通过向基础内部缓慢充气使基础浮箱缓慢起浮。根据式(4)可得到筒型基础内外液面高度差，并根据式(5)计算结构的破舱倾角φp，计算结果见表10。

表10 筒型基础—浮箱破舱倾角计算结果

由表10可知，筒型基础—浮箱外吃水深度为7 m时，破舱倾角过小，因此为避免筒型基础舱内气体溢出，气浮结构失去稳定平衡，需限制筒型基础—浮箱起浮吃水深度≥8 m(潮位高≥10.2 m)时才能进行起浮操作，此时安全液封高度大于2 m。根据表10，能够确定筒型基础—浮箱在整个起浮过程中破舱倾角为3.29°～15.88°。因此在分析筒型基础—浮箱稳性时，主要关注小倾角稳性(倾斜角度<15°)，在大倾角阶段，筒型基础舱内气体溢出，结构将失去稳定平衡状态。同样参考中国船级社《海上移动平台入级规范》[14]，筒型基础浮箱的小倾角稳性需满足自由液面修正后初稳性高不少于0.15 m。但筒型基础作为气浮体，稳性比实浮体差，稳性差异为20%～40%[19-20]，因此需要将数模得出的稳性高值均除以1.4的气浮折减系数，作为筒型基础浮箱的稳性判断依据。在SESAM软件中对筒型基础浮箱进行建模，计算整体结构在不同吃水深度下的小倾角稳性，结果汇总于表11。

表11 筒型基础—浮箱稳性计算结果

由表11可知，筒型基础—浮箱在不同吃水深度下的初稳性高满足中国船级社要求；不同吃水深度下的吊点力均不超过600 kN，小于2.1.2节中的校核值，结构有较大安全裕度。

为避免发生共振破坏，保证筒型基础—浮箱具有良好的运动性能，采用SESAM软件，通过势流边界元方法对结构进行频域水动力计算，得到不同吃水深度下筒型基础浮箱的垂荡与纵摇运动响应幅值算子(RAO)，如图14和图15所示。

由图14可以看出，筒型基础—浮箱的垂荡RAO在固有周期处出现峰值，随吃水深度的增大，垂荡固有周期增大，吃水深度8 m时峰值响应出现在9.8 s，吃水深度11.5 m时峰值响应出现在12.5 s附近；垂荡RAO幅值也随吃水增加而逐渐增大，吃水深度从8 m增加到11.5 m，垂荡运动的最大幅值增幅为40.13%。由图15可以看出，筒型基础—浮箱纵摇RAO也仅在固有周期位置出现峰值，随吃水深度的增加，筒型基础—浮箱纵摇固有周期减小，吃水深度8 m时峰值响应出现在18.4 s，吃水深度11.5 m时峰值响应出现在16.2 s。纵摇RAO幅值也随吃水深度增加而逐渐增大，吃水深度从8 m 增加到11.5 m，纵摇运动的最大幅值增幅为24.48%。在实际操作中，应避免在波浪周期与结构固有周期接近时的海况下施工，减小共振风险；该结构在11.5 m吃水深度下的运动响应较大，为改善运动性能，操作中应避免在高潮位起浮。

图14 筒型基础—浮箱垂荡RAO曲线

图15 筒型基础—浮箱纵摇RAO曲线

4 结 语

以中国广东省某海域风电场为例，提出了一种基于浮箱提高基础移位及起浮稳性的技术，并通过数值模拟对敞口筒裙—浮箱移位与筒型基础—浮箱起浮过程进行稳性与结构校核，结论如下：

1)从稳性校核的结果可以看出，敞口筒裙—浮箱移位与筒型基础—浮箱起浮过程中不同吃水深度下结构的稳性均满足要求。随着吃水深度增加，垂荡和纵摇运动的幅值最大值均有所增加，两种结构在11.5 m吃水深度下的运动响应较大，建议在10 m以下潮位工作；同时，当波浪周期接近结构固有周期时，结构可能会引起共振，运动响应较大，应避免在相应海况下施工。

2)从强度校核的计算结果可以看出，漂浮状态下，结构最大Mises应力为231.9 MPa；坐底状态下，结构的最大Mises应力为233.5 MPa，结构各构件应力均满足要求，整体结构受力较好。

3)对于海上建造的大吨位筒型基础来说，借助浮箱提高基础稳性是一种可行方案。配合低成本、建造简单、便于安装拆卸、可回收利用的浮箱，整个筒型基础的海上建造能够简便高效的批量进行，大大降低海上风电的建造成本，为未来风电发展提供新的选择。