海上环形观光平台内域水体共振响应研究

毛艳军，丁 军，马小舟，董国海

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.中国船舶科学研究中心，江苏 无锡 214082)

在当前滨海旅游业需求的推动下，大型浮式旅游平台的设计与开发具有广阔的前景。我国针对海上旅游平台的研究和建设逐渐起步，如“海上牧歌”旅游平台[1]和“耕海1号”海洋牧场综合平台[2]。在各种大型浮式观光平台设计中，在设计提供泊稳条件的游艇码头时，提出了圆环形浮式结构物的设计理念，环形结构物具有掩护作用，环内水域可作为游艇停泊区域，如中国船舶重工集团公司第七〇二研究所的发明专利概念设计模型“海洋之心”[3]。本文模型为“海洋之心”浮式观光平台概念设计的简化水动力模型，模型结构由圆环形结构主体和增加一条弦与弧围成区域作为酒店建设空间组成。环形内部水域设计功能主要为游艇码头和亲水场所，环形结构可以为游艇停泊和亲水玩水提供波浪掩护。但是随着水域封闭性增加，封闭水体也更易产生水体共振问题。典型的水体共振问题如港湾共振[4-5]，振荡水柱式波浪能发电装置[6]，以及船舶月池结构共振[7]等。因此，有内域半封闭水体的浮式旅游平台结构可能也会面临内域水体在外海透射波浪作用下引起共振而导致波高增大，泊稳条件较差的问题。

本文模型在考虑结构内域水体共振问题时更接近圆形月池共振问题，即结构形式为底部截断式环状结构，结构内部有竖井与外域联通。月池结构常见形状为矩形和圆形。月池共振问题的主要关注点为内域水体的响应频率以及在外部荷载激励下的响应幅值。Molin[7]给出了矩形和圆形月池在无限水深条件下的共振模态解析结果，可以快速进行结构的参数分析。针对圆形月池水体共振，Molin等[8]给出了有限水深的解析结果，包括活塞式共振模态和一阶晃荡模态的响应频率结果，通过与试验和数值模型结果对比，解析结果可以较好地预测月池水体共振频率。郑碧芳等[9]给出了直墙前矩形月池共振问题的解析解，研究了矩形月池结构的浮体水动力系数和波浪力变化规律，直墙的存在对于月池运动响应有较明显影响。对任意形状三维月池结构，通常采用边界元方法来求解线性势流问题。相比于物理模型试验和考虑黏性与非线性影响的黏性流计算方法，线性势流解析和数值方法都具有计算速度较快，便于设计初期的快速参数化评估的优势。在评估水域共振响应频率和模态分布中是首选方法。有较多的研究工作都采用此类数值方法研究了月池共振的响应频率问题。Ravinthrakumar等[10]采用WAMIT 软件计算了船舶矩形月池共振响应与船舶运动耦合问题的频域解，并与试验结果进行了对比，计算所得共振响应频率与试验结果吻合度较高。Vada和Pan[11]采用求解格林函数的方法给出了圆形月池的前6阶模态分布。

不同于月池结构的主要响应频率为活塞式模态和一阶晃荡模态，浮式旅游平台结构内域水体尺寸通常较大，因此更容易激发与设计海况波浪频率相近的高阶模态，该高阶模态响应频率和模态分布有待于进一步研究确定。Ravinthrakumar等[10]对矩形月池中各高阶模态的影响因素进行了讨论，当船舶在不规则波中运动时，如果月池的尺寸足够大，各高阶模态也有可能被激发。各高阶模态对于内域水体共振和结构运动响应也有较为明显的影响。

本文研究的主要目的是针对文中提出的观光平台模型进行内域水体共振响应问题分析，采用线性势流频域方法研究其内域水体共振响应频率和模态分布，分析内域水体形状对模态分布的影响以及高阶模态的响应频率和模态分布形式，进而评估内域水体泊稳条件。

1 数值模型方法

基于线性势流频域理论，采用三维边界元方法进行速度势的求解[12]，继而可以计算波面响应。

Φ(X,t)=awφ(X)e-iωt

(1)

(2)

其中，aw为入射波波高,ω为波浪频率。其中速度势函数φ(X)采用格林函数法，通过在平均湿表面上布置源来进行求解，表达式为：

(3)

其中，δ(ξ)为狄利克雷函数，G(X,ξ,ω)为满足水底和自由表面条件的格林函数，ξ为源的位置坐标，X为计算点位置坐标，S0为结构平均湿表面，Ω为计算域范围。

2 数值模型验证

表1 月池结构基本尺寸

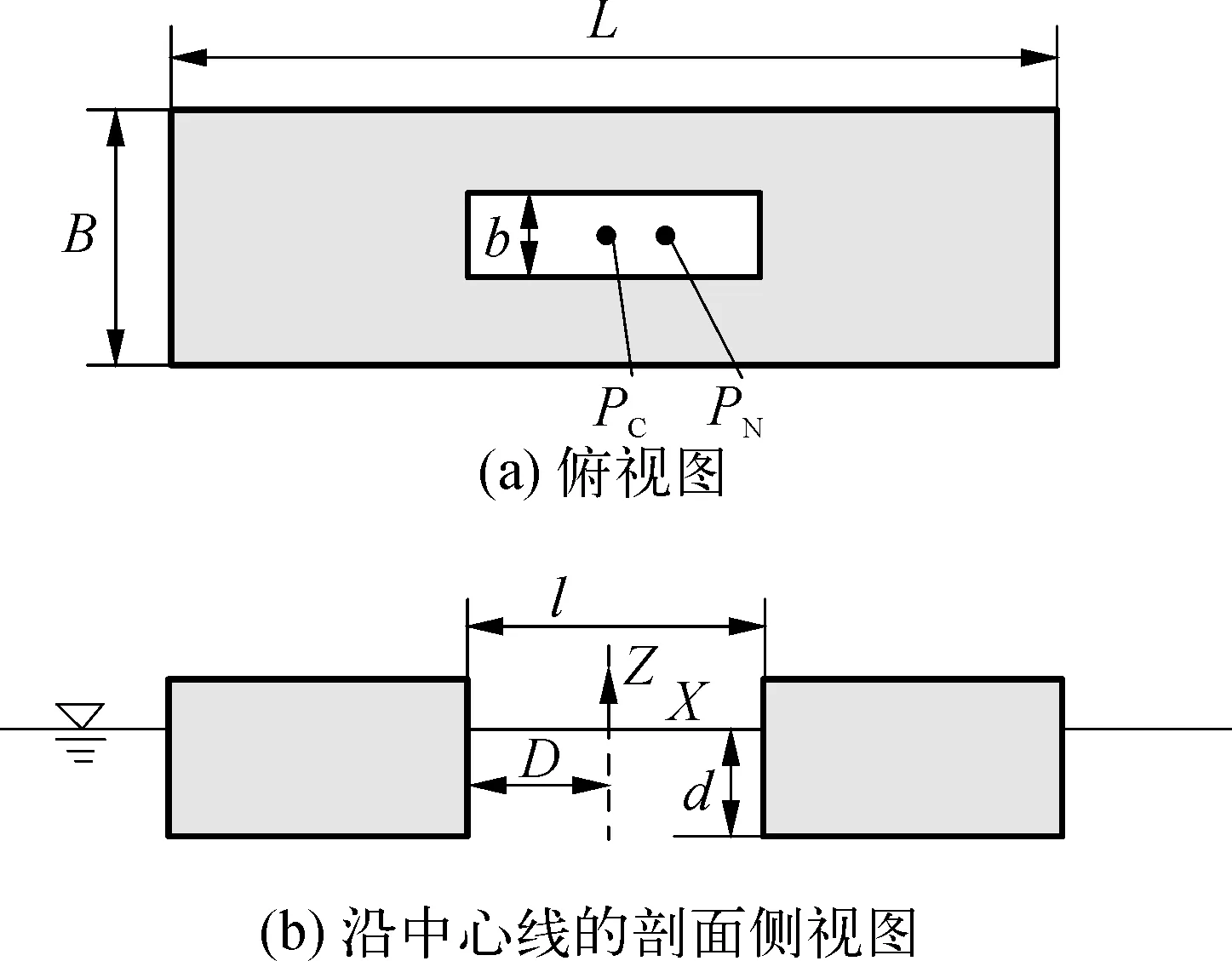
图1 矩形月池结构示意

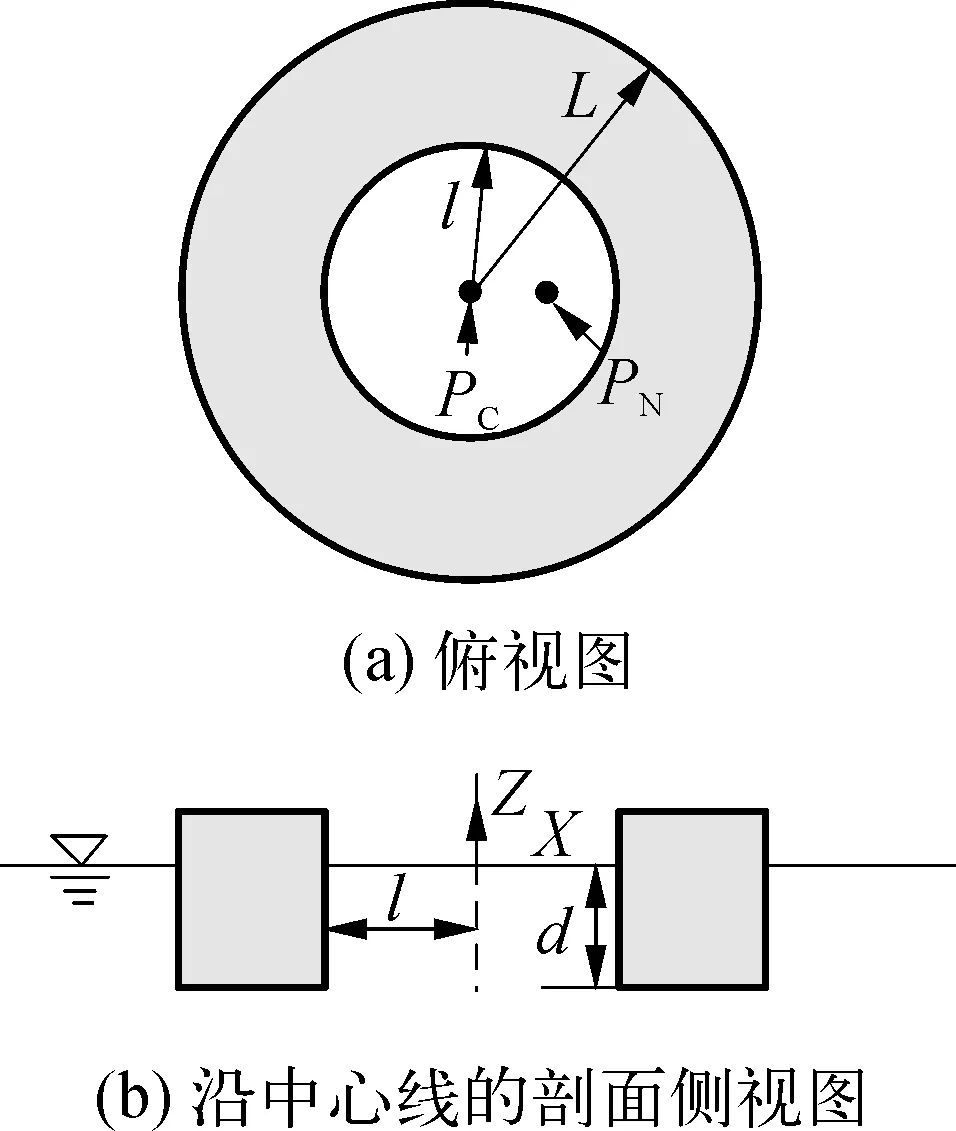
图2 圆形月池结构示意

采用ANSYS AQWA软件[12]对上述两个模型进行建模并分析月池内水体共振频率，其中矩形月池水体共振响应曲线计算结果见图3。由图3可知，采用AQWA软件计算的月池水体共振响应在活塞式共振模式以及一阶和二阶晃荡模式频率都与WAMIT软件计算结果[13]吻合较好。共振响应幅值也较为接近。通过PN测点结果可知，中心测点PC无法捕捉到一阶晃荡共振频率。圆形月池水体共振响应曲线计算结果见图4。

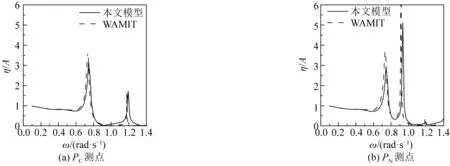
图3 矩形月池水体共振响应曲线对比结果

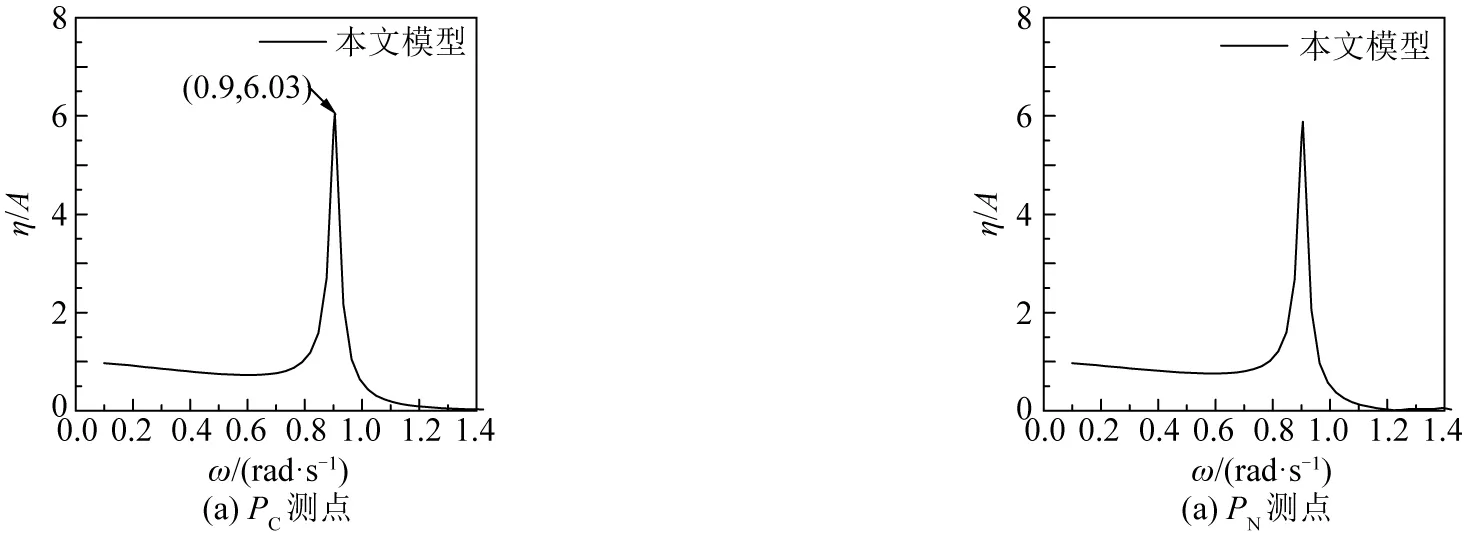
图4 圆形月池水体共振响应曲线

圆形月池水体共振响应的活塞式共振模式的频率为0.90 rad/s，与Molin等[8]的解析结果一致，表明本文模型在计算月池内水体共振频率的合理性和可行性。

3 浮式平台数值模型计算与分析

这里进行浮式旅游平台的数值模拟计算，利用AQWA来计算观光平台内域水体的频域响应。模型几何和网格划分见图5，基本几何结构为外径D=400 m，内径d=350 m的圆环形和由弦与所截圆环围成的区域，弦心距l为100 m。模型的网格划分主要采用四边形网格，部分区域采用三角形网格过渡，选取统一的网格单元长度控制参数，并在局部自动调整单元大小。计算波浪频率范围ω=0.1～1.2 rad/s，浪向为90°方向。对于大型浮式结构物，其主要运动响应共振频率较低，在常规海况波频范围内运动响应较小，因此模型假定固定不动，只考虑绕射波浪作用。

为测量模型内水体响应分布，在模型内域共布置21个测点，经过预计算结果可以发现水体响应较大位置主要是集中在y轴对称轴上和模型突出台阶部分，因此测点布置如图5(a)所示，确保测点可以捕捉到大部分峰值位置。

图5 观光平台模型

3.1 网格收敛性验证

针对观光平台模型，进行网格收敛性验证，网格尺度和单元数量见表2。选取中心测点(0,0,0)位置处的结果，观光平台网格收敛性结果见图6。

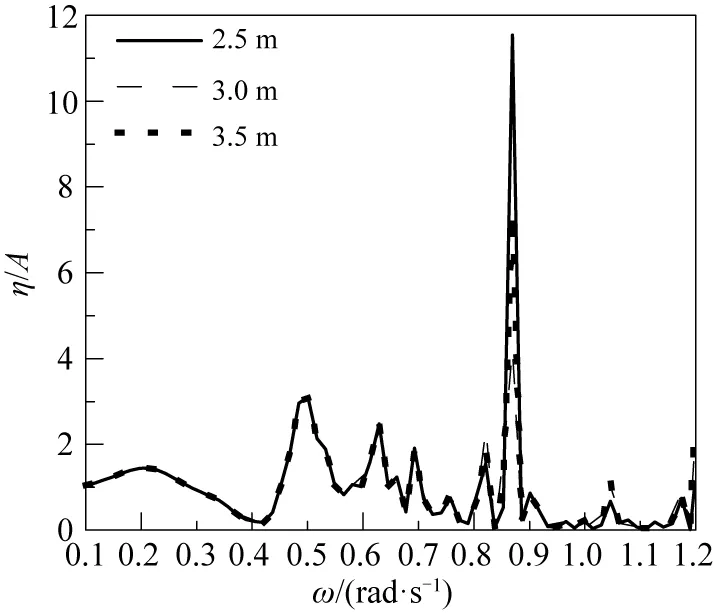
图6 观光平台模型网格收敛性验证

表2 网格收敛性验证算例设置

由模型的网格收敛性结果可知，当选取不同的网格尺度时，模型在低频部分网格收敛，响应频率以及共振响应幅值基本一致。在相对高频位置，都出现了共振幅值收敛性不好的问题，但是共振频率位置基本一致。从采用势流频域方法来寻找共振频率的角度出发，计算精度满足需求[11]。在计算波频范围不变的情况下，以下模型计算中采用统一网格控制尺寸为3.0 m。模型计算设置中采用了不规则频率消除技术，不规则频率与结构内部区域的狄利克雷边值问题的特征值相同，因此通过添加覆盖结构内部的静水面网格来模拟虚拟平均水平面并约束其垂向速度为0。扩展边界积分方程包括内部的虚拟水面积分，从而抵消不规则频率。

3.2 观光平台内域水体模态分析

首先选取弦心距l=100 m的观光平台模型作为代表工况进行模态分析，21个测点的频率响应曲线和包络线如图7所示，平台内域水体主要有6个显著的共振模态，响应频率和最大统计幅值见表3中弦心距l=100 m的结果。模态分布见表4中l=100 m的结果。文中给出的前6个响应频率存在特定的模态分布状态。由于前6个响应频率波长相对较长，流体黏性影响较小，因此表3中给出的共振幅值结果具有参考意义。因为频域计算属于稳态计算，且模型计算中没有引入阻尼耗散，导致部分响应峰值过大，如ω=0.8 rad/s位置，但对模态的识别结果无影响。势流频域模型对于响应幅值的计算需要引入阻尼修正来保证响应幅值的合理性。文中研究重点为此类结构内域水体响应模态和分布，更为精确的幅值计算可采用时域模型进行模拟。

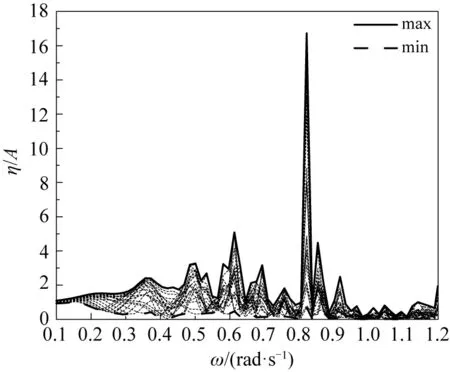
图7 模型l=100 m，21个测点叠加水体响应曲线(max, min为包络线)

表3 不同弦心距模型前6阶共振频率和最大响应幅值

不同于月池共振问题中响应模态主要是活塞式共振模态和一阶晃荡模态，平台模型的内域水体零阶响应模态不明显，响应幅值低于驻波波高。第一、二阶模态表现为晃荡模态，其波节线平行于弦，波高沿着对称轴对称分布，其最大值主要出现在对称轴上。更高阶模态分布中由于圆弧段的存在，波节线不再平直且部分模态表现出环形分布，此类分布与圆形水域固有模态中环向模态相对应。

第四，学业成就最大化的寝室氛围激励学生持续奋进。学霸寝室的学习氛围浓厚，这种浓厚的氛围饱含的巨大的正能量将寝室学生向上托举，推动他们的学习势头不断上升；而学渣寝室的氛围刚好相反，形成的向下的力量拖拽着寝室成员向上努力。向上或向下的氛围一旦形成，难以改变。学霸寝室以实现学业成就最大化的氛围推动学生积极主动地参加学术交流、学术比赛、科技创新或者为继续深造做充分准备，这种氛围的影响力和感染力无以伦比，任何学生都会深受感染和洗礼。学霸日日身临其境，在这种氛围的熏陶下，他们自然会养成一种持续拼搏的学习习惯，这正是我国在新时代实现伟大复兴中国梦对大学生的要求，也是高校培养人才的目标所在。

由以上分析可知，由于平台模型内域水体形状由弦和圆弧段组成，包含了直边界和圆形边界，在模态分布上也表现出了不同形状模态混合和占优的情况。因此下一节主要研究弦心距对水体共振模态的影响。

3.3 弦心距对平台内域水体共振模态影响分析

不同弦心距的模型对应不同的直边界和圆弧边界的组合，也对应不同尺寸的内域水体面积，选取弦心距0～175 m，间隔25 m，共8组工况进行模拟和对比分析。内域水体响应频率和最大统计幅值如表3所示，表中幅值为无量纲幅值η/A，内域水体模态分布如表4所示，表4中给出了前6阶水体共振模态，更高阶模态分布主要集中在特定位置且较大幅值区域面积较小，在时域波浪中较难被激发，这里暂不分析。所有工况中活塞式振荡模态在此结构参数下都不明显，低于驻波波高。表中l为弦心距距离，m表示第几阶显著的共振模态。

表4 不同弦心距模型前6阶共振模态分布

因内域水体形状整体保持为直边界和圆弧边界的组合形式，不同弦心距工况水体响应模态峰值频率基本保持对应。如图8所示，随着弦心距增加，内域水体面积变大，特别是沿着入射波浪向水体长度增加，各响应频率向低频方向偏移。因为直边界的存在，直边界和圆弧边界组合内域水体共振模态分布的前3阶模态分布，矩形水体共振模态分布特征占主导，即波节线趋向平行于直边界，见表4中弦心距l=100 m的工况，模态峰值主要分布在对称轴位置。

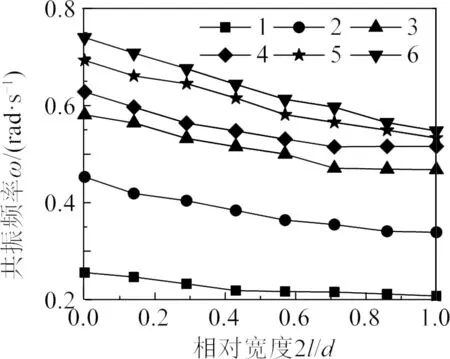
图8 各显著共振模态频率随模型弦心距变化关系

对比同一响应频率不同弦心距的模态分布特征，发现波节线的变化过程由凸形逐渐过渡到平行于弦再变化到凹形。随着弦心距的增大，直边界的影响变小，圆形水体共振模态分布特征占主导。第四、五阶模态在弦心距l<100 m时，表现出较强的环向模态特征。主要峰值分布在靠近环形边界位置，以及弦和圆弧交接的拐角位置。l> 100 m工况，波节线逐渐变直，模态峰值分布再次分布在对称轴上。

3.4 不同环形宽度对水体共振模态影响分析

不同于月池共振，本文模型在活塞式共振模态响应特征不明显，主要原因为模型水域尺寸相对较大[10]，不同环形宽度影响水域与结构尺寸的比例，因此选取环宽度b1=25 m，b2=50 m，b3=100 m三组工况研究不同环形宽度对水体共振的影响。环形结构的宽度类似浮式防波堤的结构宽度，不同宽度对应着不同的波浪透射系数，也因此引起共振模态能量聚集情况的不同。当结构环形宽度b1=25 m时，活塞式共振模态不明显，主要原因是结构宽度相对波长较小，波浪基本为无衰减透射，绕射波浪也较难在内域能量聚集，导致共振模态不明显。由图9可知，随着环形宽度的增加，前5阶共振频率向左偏移，活塞式共振模态和一阶晃荡模态峰值有明显增加。环形宽度b3=100 m工况在波频ω>0.7 rad/s后基本上没有明显振荡，但在波频ω=0.677 rad/s时有一个较为明显的振荡峰值，对应的模态分布为环向分布模态(s,n)=(3,1)。其中s对应共振模态波面分布波节线为径向波节线，n对应环向波节线分布。此外值得注意的是b1=25 m和b2=50 m工况，振荡峰值较大的模态也是环向分布模态(s,n)=(6,1)，如图10所示。

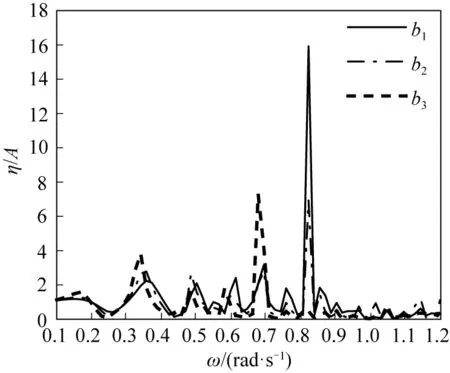
图9 不同环形宽度波高响应包络线对比

图10 不同环形宽度模型环向分布模态分布

3.5 波浪入射方向对水体共振模态影响分析

由于浮式平台在圆环形结构基础上附加台阶部分，因此平台关于y轴对称，这里考虑的波浪入射方向如图5所示主要包括0°，+45°，+90°，-45°，-90°。图11为吃水深度d=10 m时在各个波浪入射方向下中心测点1的波面升高幅值变化。可以发现平台内域水体的共振频率受浪向角变化影响较小，各浪向结果表现出相同的共振响应频率，说明该平台内域水体共振状态体现内域水体共振固有频率特性。但波浪入射方向对共振幅值具有显著影响，特别是当波浪以-90°方向入射时，波浪需要透过台阶部分后进入内域，因此在该方向上波浪共振幅值明显较小。在实际工程布置中，可将此迎浪方向布置为结构主迎浪方向，内域水体可以获得较好掩护，从而保证泊稳条件。

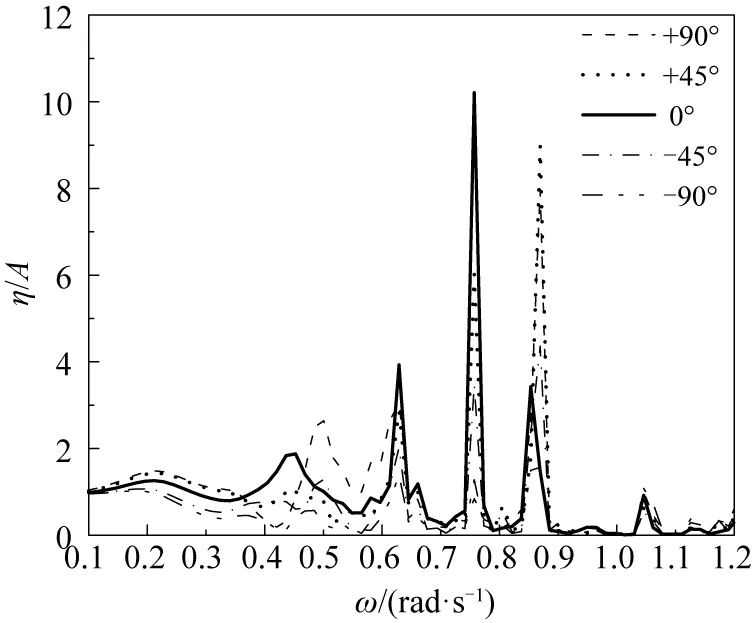
图11 不同浪向角下中心测点水体共振响应对比

4 结 语

基于线性势流理论采用频域计算方法研究了观光平台内域水体共振问题。主要研究了不同弦心距、环形宽度以及波浪入射方向对内域水体共振频率和模态分布的影响。在计算波频ω=0.1～1.2 rad/s范围内，共有6个显著共振频率和模态分布。四、五阶响应频率更接近常规海况风浪周期范围，可能是在实际应用中面临的主要影响泊稳条件的共振模态。圆弧形和直边界组合边界的水体共振模态表现出矩形和圆形水体模态混合状态，前3阶模态中矩形水体模态影响较明显，更高阶模态表现出较强的环形水体共振模态分布特征。大部分模态峰值分布在对称轴附近，部分在转角位置，因此在进行游艇码头布置时应尽可能避开。

对各影响参数分析的结论如下：

1)不同弦心距对应不同内域水体大小，随着弦心距增大，各阶共振频率都向低频方向偏移。

2)环形宽度的增加引起低阶响应峰值增加，同时短波也更难透射进入内域。

3)波浪入射方向对内域水体共振响应频率影响较小，但是不同波浪入射方向中，共振响应幅值不同，其中-90°波浪入射方向，内域水体共振幅值较小。推荐在实际布置中作为结构主迎浪方向。

文中主要针对模型进行了频域分析，未考虑黏性和非线性影响，共振幅值结果可能偏大。为准确评估共振响应大小，需进一步采用物理模型试验或考虑黏性和非线性影响的数值模型来确定共振幅值大小。