单体喷水推进船舶动力定位控制方法研究
李刚强,谌栋梁,葛 卓,周冠泽,熊 文
(1.中国船舶及海洋工程设计研究院,上海 200011; 2.喷水推进技术重点实验室,上海 200011; 3.上海振华重工(集团)股份有限公司,上海 200125)
动力定位就是船舶或海上平台不借助于锚泊系统的作用[1-2],而是利用自身装备的各类传感器测出船舶的运动状态与位置变化,以及外界风力、波浪、海流等扰动力的大小与方向,再采用现代控制理论,建立船舶与推力器的数学模型,并采用多种控制方法,利用计算机进行复杂的实时计算,对船舶各主副推力器的推力进行分配[3-5],控制船舶推力器产生适当的推力与力矩,以抵消海洋扰动力和力矩,使得船舶或海洋平台保持固定位置、艏向的控制技术。动力定位控制系统的基本原理如图1所示。

图1 动力定位控制原理
上述动力定位控制系统原理中的各个环节,国内外均已经有了较为成熟的算法:在船舶运动估计方面,多采用Kalman滤波[6]、非线性无源滤波[7]、H正无穷滤波[8]等基于船舶模型的观测器;在控制方面,主要是传统的基于荷载前馈的PD控制算法、LQR控制算法、LQG控制算法[9-12]以及模型预测控制算法[13];在推力分配方面,主要有伪逆算法、(序列)二次规划算法等[14-16]。可以说,对于装配有较多全方位推进器、侧推等的常规动力定位船舶,要实现定点控制、循迹、目标跟踪已经基本有迹可循,不难实现控制目标[17]。但对于装配喷水推进器作为主推的航行船舶的动力定位控制算法则不常见,而这类船舶尽管其主要功能是航行,但其需要定位功能的场景并不少见,如海上巡逻搜救、渡轮的自动靠泊等。Borrett和Birkinshaw[18]曾将国外Hamilton公司的喷水推进器用于动力定位控制,该喷水推进器采用了特殊的导流装置,能够产生全方位的推力,Borrett等在推力分配时将其简化为全方位推进器,且因所涉及的船舶装配了较多的喷水推进器,因此与上文所述常规动力定位船舶的控制并无本质上的区别。
喷水推进是一种特殊的船舶推进方式[19],它将水流从船底吸入,经过推进泵增速后通过喷口向船后高速喷出,利用喷出水流的作用力来推动船舶航行。通过喷水推进器上的转向和倒航装置在水平方向和垂直方向分配和改变喷出水流的方向可以实现船舶的机动操纵[20],对于只在船艉两侧各装备一个推力方向受限的喷水推进器单体船而言,要实现全方位的动力定位是比较困难的,针对此一类型的船舶,文中设计了一套算法并选择了合适的参数,采用仿真模拟的方法,验证了此类船舶实现动力定位的可行性。
1 仿真模型
1.1 缓变流作用下的船舶运动模型
船舶运动模型坐标系如图2所示,O-ξηζ为空间固定坐标系,坐标原点位于静水面上;G-xyz为固定于船舶的运动坐标系,坐标原点位于船舶重心;G-x′y′z′为水平随船坐标系,其原点亦位于船舶重心,但Gx′y′平面始终与Oξη平面平行。在船舶纵向运动幅度较小的情况下,认为G-x′y′z′和G-xyz等同。

图2 船舶运动模型坐标系
风浪流影响对动力定位控制而言是需要考虑的干扰项。当船体上层建筑受风面积较大和波浪级别较大时,开展动力定位算法研究需将风浪影响作为干扰项引入控制模型。而文中优先建立在缓变流作用下的船舶运动模型,在动力定位工况时的水平面3自由度运动方程可表示为:
(1)
(2)
式(1)为运动学方程,其中xOG、yOG为船舶重心在固定坐标系下的坐标,φ为船舶的艏向角,u、v、r分别为船舶的横向速度、纵向速度及转艏速度。式(2)为船舶运动的动力学方程,m为船舶质量,mx、my分别为船舶的纵向附加质量和横向附加质量,Izz和Jzz分别为船舶绕通过重心的垂直轴的惯性矩及附加惯性矩。XH、YH、NH为由船体与海水相对运动引起的除开惯性力以外的作用于船体上的纵向力、横向力及转艏力矩,XP、YP、NP为螺旋桨所施加于船体上的纵向力、横向力及转艏力矩。船体的质量/惯量对具体船舶的具体加载工况可以认为是已知量,附加质量惯量则可以通过势流理论计算得到。
黏性类流体动力XH、YH、NH的计算相对复杂,就船舶的动力定位工况而言,可以采用式(3)~(5)进行估算:
(3)
(4)
(5)
式中:XH的计算参考了船舶阻力计算公式,UC为相对海流速度,β为该流速与船舶纵向x之间的夹角,S为船舶湿表面面积,Re为雷诺数。
(6)
式中:L为船长,υ为海水的运动黏性系数,取1.05×10-6m2/s。YH、NH的计算采用了横流公式,CD(x)为船体横截面x处的阻力系数,D(x)为船体横截面x处的吃水。
1.2 喷水推进器及其控制
如前所述,喷水推进器通过向船后喷水以产生推力[21],就动力定位工况而言,可以认为喷水推进器处于系柱状态,在此状态下,喷水推进器消耗的功率P与转速n立方成正比,比值为CP。
P=CPn3
(7)
系柱状态下喷水推进器的名义推力T(此处指不经过倒车装置作用所发出的推力)与转速n平方成正比,比值为CT。
T=CTn2
(8)
在这点上,喷水推进器与常规的用于动力定位的全方位导管桨是一致的。为改变喷水推进器推力的大小和方向,通常可以通过控制转速、倒车斗、方向舵来实现。通常可以实现如图3所示两种推力曲线包络图,其中图3(a)对应国内某研究所相关产品,图3(b)为国外某喷水推进器的包络图。该推进器通过增加侧向导流装置的方式来实现全方位推力包络图,本文所用推进器为图3(a)所示。
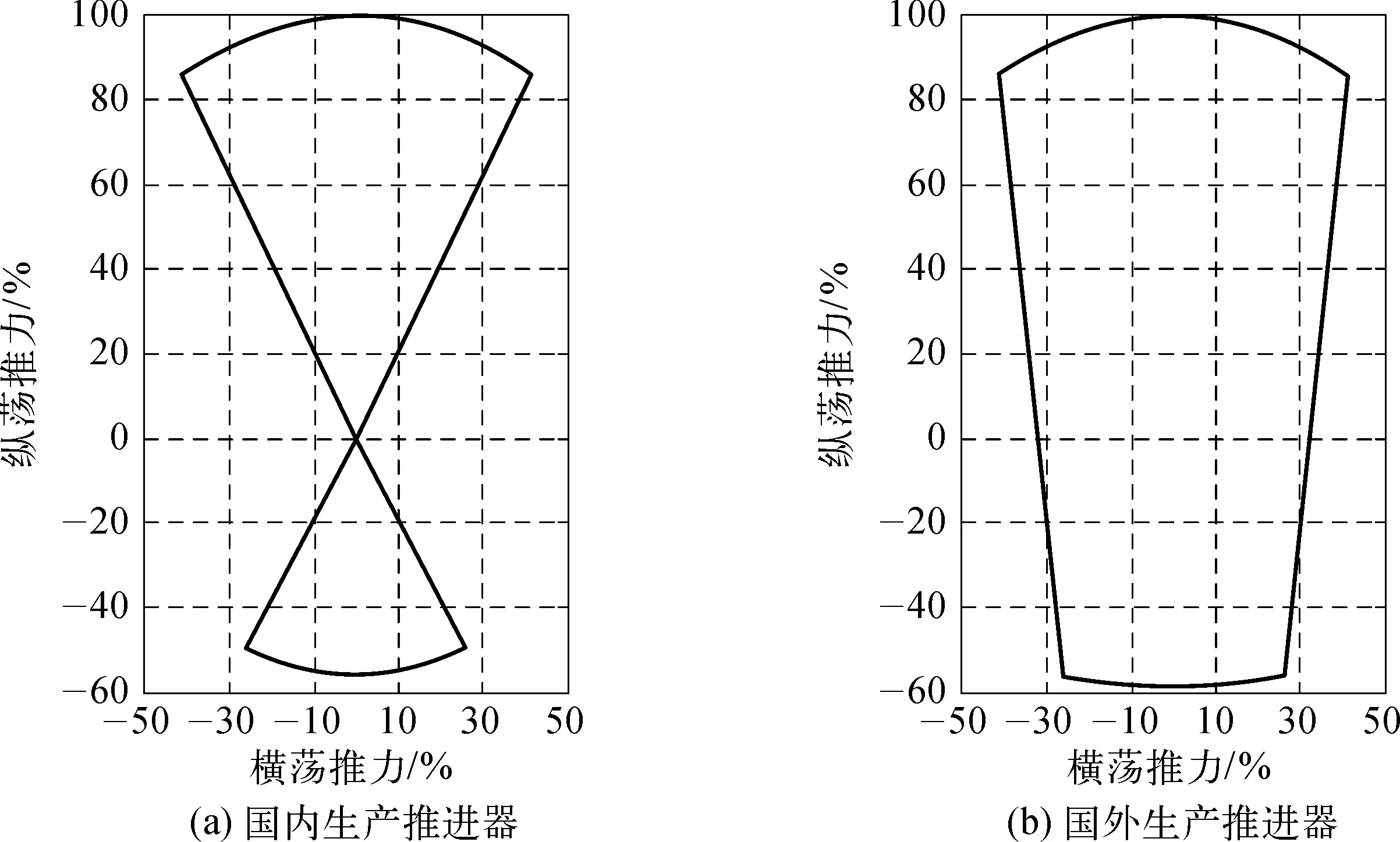
图3 推进器推力包络图
喷水推进器的转舵控制响应可以用式(9)模拟:
(9)
式中:TE为时间常数,δcom为舵角指令,δ为舵角。同样,喷水推进器的倒航控制亦可以用类似的一阶系统模拟。
2 船舶运动Kalman滤波
2.1 Kalman滤波原理简介
对于如下所示的连续系统,
(10)
其中,x为状态变量,u为控制变量,w为单位时间干扰强度为Q(t)的白噪声。假设该系统在时刻t的状态变量和协方差分别为xt、Pt,经历较小的时间间隔Δt以后,假设在此过程中没有对系统进行观测且此一时间间隔内控制变量已知,则t+Δt时刻的系统状态变量可由式(11)和(12)估计:
xt+Δt=Integ{f[x,u(t)],Δt,xt}
(11)
(12)
其中,Integ代表对式(10)所代表的常微分方程进行积分求解,Φt,t+Δt为一步转移矩阵,通过式(13)进行计算:
(13)
不失一般性,对于在时刻t由式(10)所描述的状态变量和协方差分别为xt、Pt的系统,对该系统进行如式(14)所示的观测:
y(t)=h(x,t)+v(t)
(14)
其中,h(x,t)为测量方程,v(t)为测量误差。假设v(t)为强度R(t)的白噪声,那么经由观测向量校正后的系统状态变量及其协方差可由式(15)~(17)计算:
(15)
(16)
(17)
其中,Ht为测量方程对状态变量x的偏微分,
(18)
2.2 用于滤波的船舶运动模型
如上文所示,Kalman滤波算法是一种基于模型的观测算法[22],为了采用该算法,首先必须确定式(10)中的f[x,u(t)]。针对船舶在风、浪、流作用下的船舶运动,采用式(19)~(24)对船舶进行运动滤波。
1)船舶低频运动模型:
(19)
(20)
其中,xL,yL,ψL为固定坐标系下船舶低频运动的坐标和艏向;uL,vL,rL为运动坐标系下船舶低频运动的纵向、横向速度和转艏角速度;τthru为推进器推力向量,τwind为风力向量;Xuu,Yvv,Nrr为船舶的纵向、横向和艏向二阶水动力系数;uc,vc,rc为流速在纵向、横向和艏向的分量;wu,wv,wr为具有一定强度的白噪声,表示船舶低频运动模型的误差;M为船舶惯性矩阵。
2)船舶波频运动模型:
(21)
(22)
(23)
其中,xH,yH,ψH为船舶波频运动的纵向、横向坐标和艏向角;ξx,ξy,ξψ为船舶波频运动的纵向、横向坐标和艏向角的积分状态变量;ζx,ζy,ζψ为相对阻尼系数;ω0x,ω0y,ω0ψ为波频;wx,wy,wψ为零均值高斯白噪声;Kwx,Kwy,Kwψ为高斯白噪声增益(基于海况)。
3)流干扰模型:
(24)
其中,Vc,βc为流速和流向;wvc,wβc,wrc为零均值高斯白噪声。
有了船舶运动的预测模型,尚需采用传感器对其进行观测方可得到船舶的运动状态。一般而言,动力定位船舶均需配备用于测定位置的位置参考系统和测定艏向的罗经[23]。对于一般的位置参考系统,假设其所测得的位置均可转化为固定坐标系下的位置,则观测方程可表示为:
(25)
其中,xins,yins为位置传感器的安装位置;vN,vE为位置测量误差。为简单起见,这里没有考虑横摇和纵摇的影响。
对于罗经类传感器,其观测方程可表示为:
hgyro=ψL+ψH+vHd
(26)
其中,vHd为位置测量误差。
3 船舶动力定位控制
3.1 基于荷载前馈的PD控制算法
在定点定艏向等控制中,以观测器——文中为Kalman滤波器所得到的船舶位置、速度以及除推进器以外的荷载信息为输入,采用式(27)计算船舶动力定位控制中所需推力和力矩:
(27)
其中,Psurge,Psway,Pyaw为比例常数;Dsurge,Dsway,Dyaw为微分常数;δbias, surge,δbias, sway,δbias, yaw分别为横向、纵向以及转艏与目标的偏差,τext_1、τext_2、τext_3分别为已知的外界横向、纵向和转艏力矩。
3.2 进入自动模式时的控制策略
在动力定位的实际操作中,动力定位操作员按下操作指令后,控制系统会先将船舶速度降低,然后选定船舶的当前位置和当前艏向作为定位目标,这一过程中的控制策略为:
(28)
3.3 转变目标位置和艏向时的控制策略
动力定位船舶转变定位的目标位置点和艏向时,其控制可以分为两个阶段,第一阶段以系统指定的移位速度为控制目标,沿当前目标位置与新的目标位置之间的连线进行控制:
(29)

船舶改变艏向时的控制策略与转变目标位置点时的控制策略相似,此处不予赘叙。
4 推力分配
4.1 基于广义推进器的二次规划方法

(30)
所有r台推进器的总推力可表示为:
(31)
推力分配的总目标是在能量消耗最小的情况下使得推进器所分配得到的推力尽可能等于目标推力[17],引入松弛变量s来表示二者之差,并假设推进器所消耗的能量与推力大小平方成正比,则推力分配可表示成如下极值问题:
(32)
式中:H和Q为权矩阵。满足约束条件:
(33)
对用于动力定位的常规推进器如侧推、全方位桨在以一个较小的时间步上,其推力约束均可以简化为线性不等式的组合[16],因此推力分配问题就可以转化为一个经典的带图约束的二次规划问题求解。此问题已有较为成熟的解法,且局部最优解即为全局最优解。
4.2 针对喷水推进器的特殊处理
文中所采用的喷水推进器的推力包络图如图3(a)所示,可知在推力分配时其约束难以转化为凸约束,为利用上述二次规划方法求解,可以将每个推进器分成正推和倒推两种情况,即对全部r台推进器所组成的推力分配问题,可通过求解2r个子问题的方式得到其最优解。采用分正推和倒推情况进行处理后,喷水推进器推力分配的局部约束条件与全回转推进器推力分配的局部约束条件类似,其推力约束详见图4。

图4 喷水推进器推力约束
Fx,i,Fy,i在分配时应当为图中直线1、2与圆弧3、4所围成的区域。在具体计算时圆弧3用直线5近似,圆弧4用直线6与直线7近似,因此由直线6、7、5、2、1围成凸五边形,该五边形对编号为i的推进器的约束可表示为:
(34)
5 仿真模拟
5.1 目标船舶主要参数
为了验证算法的可行性,以一艘单体喷水推进船舶作为目标对象,对动力定位工况下常规操作进行了模拟。目标船基本信息为:水线长11 m,型宽3.4 m,型深1.2 m,吃水0.48 m,排水量8.5 t。船艉左右两侧各装备一台喷水推进器,该型推进器可在±30°范围内调整推力方向,其推力性能见表1。模拟过程中,所涉及的主要控制器PD参数见表2。

表1 目标船喷水推进器性能

表2 动力定位算法控制参数
5.2 无干扰条件下仿真结果
首先开展无干扰条件的仿真试验,即模拟时不考虑风和浪,只添加缓变流,流的大小约为0.617 m/s,来流方向约为340°。
1)从自由漂浮状态进入自动定位
开始时,船舶处于流作用下的自由漂浮状态,模拟自动定位操作控制后船舶的运动状态。图5为此过程中船舶的北向位置、东向位置以及艏向的时间变化历程。可以看出,系统在收到自动定位指令后,船舶迅速减速后选定当前位置和艏向(图上目标位置北向、东向均为0 m,目标艏向角60.5°,之所以为0 m是数据处理过程中将原点选在此点)作为控制目标,然后一直保持该位置和艏向,定位效果非常好。图6为此过程中的命令推力、分配推力与实际推力三者之间的对比,可以看出分配推力与命令推力符合得较好,证明推力分配算法工作正常,实际推力较命令推力有一定的滞后,此为执行机构存在滞后所引起。

图5 船舶位置、艏向时历—进入自动定位

图6 命令、分配及实际推力对比—进入自动定位
2)变换目标艏向
在稳定定位的基础上,将目标艏向角调整至0°,图7为此过程中船舶的位置及艏向变化时历,图8为命令推力、分配推力与实际推力的对比。从模拟结果可以看出,改变目标艏向的过程中,船舶位置稳定,推力分配算法亦运行良好,船舶转艏至新的目标艏向后,亦能稳定的定位在该新目标艏向。

图7 船舶位置、艏向时历—转换目标艏向

图8 命令、分配及实际推力对比—转换目标艏向
3)转变目标位置
在稳定定位的基础上,转变目标位置至(-40,-40),图9为此过程中船舶的位置及艏向变化时历,图10为命令推力、分配推力与实际推力的对比。
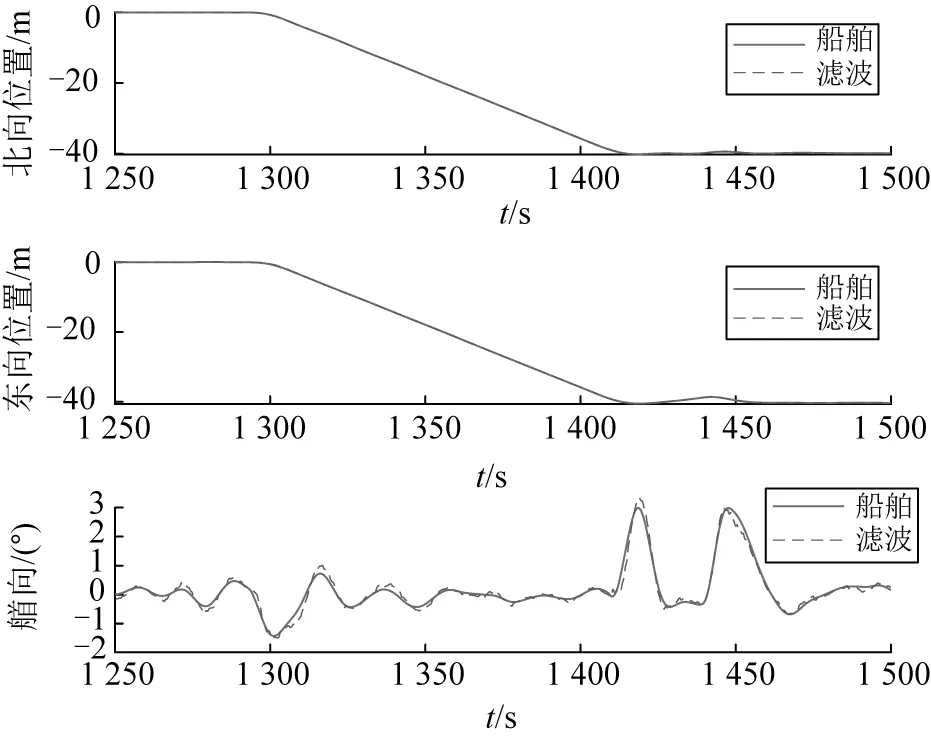
图9 船舶位置、艏向时历—转变目标位置

图10 命令、分配及实际推力对比—转变目标位置
从图9中可以看出除在船舶从原目标位置加速以及达到新的目标位置减速这两个阶段中船舶艏向出现较大——约3°的波动外,整个移位过程中,船舶艏向控制良好,船舶移位至新的目标位置后亦能稳定的定位在新的目标位置。从图10可以看出,造成此艏向波动的原因在于在船舶加、减速的过程中分配推力与命令推力之间出现了较大的偏差。造成分配的推力跟不上命令推力的原因在于系统推力不足,此种情况下可通过减小移位目标速度改善。
4)转艏至艉部来流失位模拟
由于喷水推进器倒推的推力要远小于正推力,经控位能力分析表明艉部来流时,船舶不具备稳定定位的能力,文中通过位置自动控制下的持续转艏对此情况进行了模拟。图11为此过程中船舶的位置及艏向变化时历,图12为响应时历上命令推力、分配推力与实际推力的对比。

图11 船舶位置、艏向时历—持续转艏
从图12中可以看出,当船舶转艏至140°、相对来流为158°时分配推力中的横向力明显跟不上命令的横向力,此亦因系统推进能力不足所致,与之对应,船舶开始失位。当船舶转过来流对应的对称角度即转至约190°后,分配的推力开始跟上命令推力,船舶开始减小定位误差,直至定位至原来的目标位置。

图12 命令、分配及实际推力对比—持续转艏
5.3 风浪干扰条件下仿真结果
进一步基于前述针对船舶在风、浪、流作用下的运动滤波模型,对其在有风浪干扰下开展了定位控制仿真试验。试验条件设置为风速10 m/s,有效波高1 m,流的大小约为0.617 m/s,来流方向约为340°。试验结果如图13和图14所示,图中可以看出,在存在外界干扰条件下,虽然船舶位置和艏向在扰动下会产生偏离,但通过所设计的控制算法能在较短时间内恢复原位置,取得较好的定位效果。

图13 船舶位置、艏向时历—定位(有干扰条件)
6 结 语
以一型单体喷水推进船舶为研究对象开展了动力定位算法设计及仿真试验研究。文中以Kalman滤波器所得到的船舶位置、速度以及除推进器以外的荷载信息为输入,基于荷载前馈的PD控制算法并综合考虑喷水推进器特殊的推力分配原理,设计出可用于单体喷水推进船舶动力定位的控制算法,实现了定位、移位及改变目标艏向等基本的动力定位操作,并通过仿真试验进行了验证。可以认为对于单体喷水推进这类并非设计用于动力定位作业的船舶,在外荷载较小的情况下,只需避开特定的外部荷载方向而使得外加纵向荷载补位较大正值,则可以实现动力定位的基本功能。

