深海多金属结核生长模拟及宏观形貌研究
王华昆,高 婧,蔡毅华,余 杨,孙震洲,李修波
(1.福建省滨海土木工程数字仿真重点实验室(厦门大学),福建 厦门 361005; 2.近海海洋环境科学国家重点实验室(厦门大学),福建 厦门 361005; 3.水利工程仿真与安全国家重点实验室(天津大学),天津 300072; 4.华东勘测设计研究院有限公司,浙江 杭州 311122; 5.中车SMD(上海)有限公司,上海 201360)
自20世纪70年代起,海洋学家对深海矿物的研究就没停止过[1]。研究表明[2-3]:全球大洋底部多金属结核总量约(2~3)万亿t,太平洋约有1.7万亿t,其中约有540亿t干结核含6.5亿t的Ni、5.2亿t的Cu、1.15亿 t的Co和100亿t的Mn,这些矿产资源将成为未来开发的目标[3]。多年勘探表明太平洋的克拉里昂—克利珀顿区(CCZ)是结核资源最丰富的区域,多金属结核位于热带太平洋东北部水深3 700~5 500 m处,面积约4.5×106km2[4-5]。实践表明:水力输运是当前最具商用前景的深海采矿方式[6],该系统中的垂直水力运输系统(VTS)将海底结核输运至水面采矿船。矿浆液通过离心泵和在立管内输运时会发生颗粒破碎,颗粒破碎会影响到水力输运效率,因此,需要对颗粒的破碎机理和规律进行详细研究。
要确定结核的冲击破碎机理,需对结核几何外形、微观结构、强度特性有准确的认识。因此必须了解结核的生长全过程。多金属结核的形成至少需具备以下几个条件[7]:1)具有赖以生长的核心物质;2)具有一定的稀有金属来源,矿物的元素主要通过水成作用或成岩作用,也可能是两者的结合[8];3)具有一定的构造机理;4)适宜的地球化学环境。深海多金属结核的生长过程、生长速率可通过生长年代测定进行分析。常用年代测定方法包括[9-10]:10Be测年法、铀系放射性测年法、Sr同位素地层学法、经验公式法(如Lyle公式[11]、Manheim公式[12]、Puteanus公式[13]等)、生物地层学法[14]、Os同位素地层学法[14-15]等。上述方法在时限、准确度上均有一定的局限性,对于生长年龄较小的结核(<15 Ma),10Be测年法是目前最精确的测年方法,但由于10Be半衰期为1.5 Ma,对于生长年龄大于15 Ma的结核则无法精确测定。此外,该法测试费用昂贵,且无法识别多金属结核的生长间断[10]。放射性年代学和生物地层学法是最为常见的方法,由于U系核素的半衰期较短,U系年代学方法只能用于测定结核表层约1~2 mm的年龄[10,14],而Os同位素地层学法具有灵敏度高、不易受外界干扰等优势,可以准确测定的时间尺度高达65 Ma[16]。
目前关于结核颗粒破碎的研究都是基于试验的[3,17-19],得到的破碎规律实际上强烈依赖于结核本身特性(结核外形、微观结构)及采用的水力输运条件(包括管径、泵几何参数、转速等)。结核破碎除了与碰撞速度和角度有关外,与结核本身的微观结构、强度、形状、密度等固有特性是息息相关的,目前尚未见准确的结核冲击破碎仿真研究。由于结核形状极其多样,会显著影响结核冲击破碎过程,进而影响水力输运过程,可能诱发堵塞,而目前尚未见结核形状准确的模拟方法。因此,本研究旨在提出结核生长数值模拟方法,通过模拟结核生长全过程,得到合理的结核几何模型,为结核冲击破碎仿真几何模型建立提供基本方法。
1 多金属结核生长数值模拟方法
1.1 多金属结核的构造特征
尽管文中仅对宏观外形进行仿真,尚不涉及微观结构模拟,但了解微观结构有利于加深对结核生长过程的理解,提高模拟方案的合理性。
多金属结核均由沉淀物围绕核心物质向外生长形成壳层,由于沉积过程与海洋环境(如洋流活动等水动力条件、当地沉积物种类等)紧密相关,其结构往往非常复杂。多金属结核呈数厘米至数十厘米的颗粒状[10,19],根据多金属结核的尺寸可将其分成大型(dp>6 cm)、中型(3 cm 尽管多金属结核结构构造复杂多变,但从宏观上看结核可视为由核心、壳层两部分组成,如图1、图2所示。核心物质可能是老的结核碎片(铁锰质),也可能是岩石碎屑(火山岩、沸石、磷灰石、蒙脱石、蚀变玄武岩、花岗闪长岩[10]等)、生物骨骼(鱼骨、鱼的牙齿)、铁锰矿物及黏土等[2]。结核核心也可能发生蚀变褪色,导致气孔发育,这些气孔一般呈不规则圆形或椭圆形,且大小不一,部分气孔中可能有杏仁或铁锰物质充填[10]。而壳层主要由厚度不等的纹层围绕核心生长而成[10](见图1)。各壳层间并非均匀等厚,其致密度也具有很大差异。吴长航[10]研究表明,南海多金属结核壳层具有非常明显的内外双层结构(图1)。其中外侧为致密层,在表层以下2 mm左右,该致密层硬度相对较大,杂质较少,具平行纹层状构造。而内层结构疏松,含大量孔隙和粗颗粒杂质,纹层构造不清晰,主要为斑杂状构造、树枝状构造。不同的构造类型能够反映结核形成时的海洋环境信息,在环境稳定、生长缓慢的条件下,壳层的构造一般呈致密的纹层状、柱状,一般为水成型结核;在沉积环境变化剧烈、结核生长速度较快的条件下,壳层的构造一般呈斑杂状和树枝状,且微层弯曲较大,壳层结构疏松[10]。此外,根据多金属结核的表面特征可将其划分为光滑型(S型)、粗糙型(R型)和顶面光滑—底面粗糙的混合型(S+R型)三种结核[10,24]。结核表面光滑程度与其成因类型息息相关[19]。一般外表光滑的S型结核属于水成成因,出现在和海水可以直接发生接触的沉积环境中,对应的成矿过程缓慢均匀,壳层致密;而表面凹凸不平的R型结核属于成岩成因,大多被海底沉积物掩埋;而S+R 型是混合成因,其形成过程包含了水成成因和成岩成因[10]。此外,研究表明:各种形态类型的结核产出与地形有密切关系,见表1[2]。这种形态差异可能与结核所在海山或平原的局部流体流动条件有关(局部洋流的流动差异可能影响沉积物的沉积和分布)。多金属结核不仅外形复杂多变,其微观结构也非常复杂,如图1(b)所示[10]。典型壳层构造包括块状、斑状、柱状、纹层状、脉状和领状等[10],由于文中目前只关注结核宏观外形及尺寸随时间变化,因此,对微观形貌、结构致密性和纹理暂不做分析。 图1 CCZ中的锰结核分布及断面构造和多金属结核SO4-1DG-1的镜下显微构造 图2 深海多金属结核形貌[4, 10] 表1 结核形态与地形的关系 多金属结核生长速率极其缓慢,一般在1~10 mm/Ma 之间[10,25-28]。Neff等[27]采用热电离质谱(TIMS)法对南海水域铁锰结壳进行U系放射性定年测量,得到的生长速率为1.5±0.15 mm/Ma。何高文[28]研究表明,多金属结核的平均生长速率(3.0 mm/Ma)略高于结壳(2.37 mm/Ma),典型生长速率范围在 2~4 mm/Ma之间,且以 2~3 mm/Ma为主,该值与夏明和张承蕙[25]给出的南海锰壳层表层的生长速率上限值(4 mm/Ma)极为接近,刘韵[26]关于南海多金属结核的生长速率测试结果也进一步证实了上述测量结果的可靠性(3.5~4.7 mm/Ma)。然而Frank等[29]的测量值比上述值大得多,其研究表明水成型、成岩型和热液型结核(壳)的生长速率分别高达 1~15 mm/Ma、10~100 mm/Ma 及大于1 m/Ma[10]。一般来说不同海域、不同成因的结核生长速率均有较大差异,深海多金属结核(壳)生长速率较低,而浅海和边缘海区的生长速率较高[10]。在吴长航[10]的研究中也检测到极高的结核生长速率,通过采用放射性10Be对多金属结核样品的生长速率进行检测,研究表明南海北部陆缘多金属结核生长较快(生长速率范围在2.89~74 mm/Ma之间,平均值约7.41 mm/Ma,可见结核在形成过程中生长速率波动剧烈),而位于南海中央海盆北部的多金属结核平均生长速率则小得多(3.55 mm/Ma),印度洋多金属结核的生长则更慢,其中结核内侧壳层的平均生长速率为2.16 mm/Ma,而外侧壳层生长速率只有1.95 mm/Ma。一般来说,结核结构致密程度与生长速率呈反比,生长越快,结构越疏松,所含杂质越多,典型的结核生长速率如表2所示[10,14-15]。 表2 不同矿物的生长速率 根据1.2节所述,尽管结核生长速率极其缓慢,但在不同时间段和不同海域都存在较大的离散性[10]。根据段飞达[14]的检测结果(见表2),假定结核生长速率满足正态分布,对应的概率密度函数为: (1) 其中,μ为均值,σ为标准差。对应的均值和标准差均列于表2。文中结核生长模拟方案为: 1)首先假定一核心物质的形状及尺寸,典型的如颗粒状砾石、板岩、鲨鱼牙齿及鱼骨,并建立相应的几何模型; 2)通过预定的生长模型(由试验确定)控制核心物质表层网格节点坐标移动,模拟结核生长,其中节点移动方向由共享该节点的单元表面法向量的矢量和确定,移动距离由生长速率模型确定[式(1)]。 整个模型均为ALE(arbitrary lagrangian-eulerian)自适应网格计算域,其中核心物质外表面为矿物沉积界面,该表面上的网格节点移动速度和方向由自定义Fortran子程序控制。模型考虑了沉积过程的随机性,实际沉积速率由对应的均值和标准差确定。整体数值模拟方案如图3所示。 图3 数值模拟流程 根据图3的数值模拟方案,对典型的不同核心物质进行数值模拟,核心物质包括鲨鱼牙齿[30]、鱼骨[31]、岩石碎屑、球状鹅卵石(图4)。 (a)鲨鱼牙齿 相应的有限元模型均做了一定简化,以便得到高质量的网格。模型生长速率取2.25 mm/Ma, 变异系数δ=0.3。不同核心物质经过不同年限生长后的外形模拟结果如图5所示。 图5 不同核心物质随机生长过程(单位:mm,生长速率为2.25 mm/Ma, δ=0.3) 计算结果表明:该模拟方法可有效地对结核随机生长过程进行模拟,无论初始的核心物质是什么形状。但不同形状会影响允许的模拟时间。尤其是模型中存在小几何面和复杂外形的情况[图5(a)、5(b)虚线框],在较短的模拟时间后,这些小几何面和夹角因节点移动会导致网格畸变,使网格质量大大降低,甚至出现扭曲和反向,导致计算终止。对于相对简单的几何形状(如近球形核心物质),该方法可实现长时间模拟(如十几个百万年)。 根据段飞达[14]实际的检测数据(见表2),典型的结核生长速度变异系数大约为0.035~0.076,该变异系数对应测量得到的沉积速率均较小,但在结核生长过程中存在快速生长期,对应的环境剧烈波动[10],可假设对应的生长速度变异系数更大。因此,对不同变异系数的结核生长过程进行模拟,模拟结果如图6所示。计算结果表明:沉积速率离散性也是影响沉积过程模拟时间的主要因素。事实上,段飞达[14]测量得到的沉积速率变异系数远小于这里数值模型采用的最大变异系数(δ=0.50),在大变异系数下,节点生长速度剧烈波动,即使采用网格平滑算法,也很难保证网格不扭曲,相应的容许模拟时间也小得多。若采用段飞达[14]给出的小变异系数,该方法可实现更长时间的模拟。在均匀生长的条件下,结核壳层生长后的形状与原核心物质一致。 图6 不同变异系数结核形态对比(单位:mm,T=0.55 Ma) 根据吴长航[10]对SO4-1DG-1多金属结核的检测结果,结核在生长过程中分6个典型阶段,各阶段生长速度均有较大差异,生长速率变化范围在2.89~74 mm/Ma之间。因此,单一的生长常数往往不能很好地刻画结核生长全过程,针对这一问题,采用上述方法,进行多阶段生长模拟。各个阶段的生长参数不同,如表3所示。SO4-1DG-1大小约为 6.5 cm×5.5 cm×6 cm,初始生长点对应的取样深度约为2.29 cm,核心呈不规则球形,假定其核心为球形,由此可确定其核心直径约为1 cm(按最小尺寸确定),将其作为初始球形核心进行模拟。根据段飞达[14]的测试结果,计算得到典型的生长速度变异系数在0.035~0.077之间(见图7),但其测试得到的典型生长速率均较小,远小于吴长航[10]和Frank[29]给出的生长速率极大值。研究表明:生长速率大的阶段沉积环境剧烈动荡,可认为对应阶段的沉积速率变化较大,因此,文中快速生长期采用的变异系数比沉积速率慢的阶段更大,计算数据如表3所示。 图7 生长速率变异系数 表3 南海北部多金属结核生长速率测定结果 根据表3所示参数,对SO4-1DG-1多金属结核的全寿命生长进行仿真,将不同节点计算结果和吴长航[10]测试结果绘于图8中。其中前3个阶段模拟结果与测试值极为接近,由于在第4个快速生长期引入了较大的变异系数,导致第5个阶段模拟值与测试值正负偏差均较大(测试值给出的是生长厚度均值),但这种差异也反映了沉积过程的随机性和不均匀性,采用更小的变异系数可使模拟结果与测试值更加吻合。不同阶段的结核外形如图9所示,尽管阶段4生长速度率极大,但由于其生长时间较短,对结核尺寸影响并不十分显著。图8中也给出了结核体积随时间变化曲线,由于结核外表面面积随着结核生长快速增大,允许更多的矿物同时沉积,导致体积增长速度越来越快。 图8 时变沉积厚度 图9 不同阶段的结核外形(单位:mm) 鲍才旺等[19]和吴长航[10]研究表明:结核外表的光滑程度与其成因类型紧密相关。一般认为,S 型结核多属水成成因,该型结核形成于和海水可以直接接触的沉积环境中,对应沉积过程缓慢均匀,形成的结核外表光滑且致密;而R型结核主要是成岩成因,该型结核多被海底沉积物所掩埋,形成的结核表面凹凸不平,较为粗糙;S+R 型属混合成因,包含水成和成岩成因。 针对上述不同成因问题,采用球形核心物质模拟结核埋置在海底沉积物不同深度的结核生长过程,模拟过程忽略海床表面的变化,分析S+R 型结核长期生长后的形貌。作为简化,假定与海水接触结核表面平均生长速度为2 mm/Ma,δ=0.1,而埋置在海床中的部分平均生长速度为5 mm/Ma,δ=0.3,针对结核在海床中的不同埋置深度(Zbed,Zbed=0表示球形核心物质的中心Z坐标),得到典型的模拟结果对比如图10所示,其中R表示初始核心物质的半径。研究表明:埋置深度对结核形貌影响很大,S型结核表面光滑,生长速度慢,R型结核表面粗糙,生长速度快。结核埋置深度Z=0的模拟结果与图2(c)中的SO4-1DG-1结核剖面极为相似,因此SO4-1DG-1结核应该是半埋置在海床中的。根据图10(d)、10(e)中的模拟结果可知:埋置深度会极大影响结核的最终外形,包括形状和局部光滑程度。目前,文中模型尚未考虑局部流动环境对沉积过程的影响,后续研究会进一步考虑局部洋流对矿物传质过程的影响,以得到更合理的结核几何模型。 图10 不同埋深的S+R 型结核形态(单位:mm) 提出了多金属结核宏观形貌的全寿命生长模拟方法,得到以下几点结论: 1)通过控制网格节点移动可有效模拟多金属结核多阶段随机生长过程,该方法可有效处理结核几何拓扑变化较小的生长过程; 2)生长速率变异系数和核心物质几何不规则(包括小几何面和相贯几何)是导致该方法无法长时间模拟的主要原因,因为这些因素容易导致网格畸变; 3)不同核心物质形状、沉积速率变异性、核心物质在海床淤泥中埋置深度是影响结核形态的主要因素,其中矿物沉积速率的变异性是影响结核表面光滑度的主要因素,对于实际结核生长,应考虑结核在海床上的静置形态,以获得更合理的几何模型。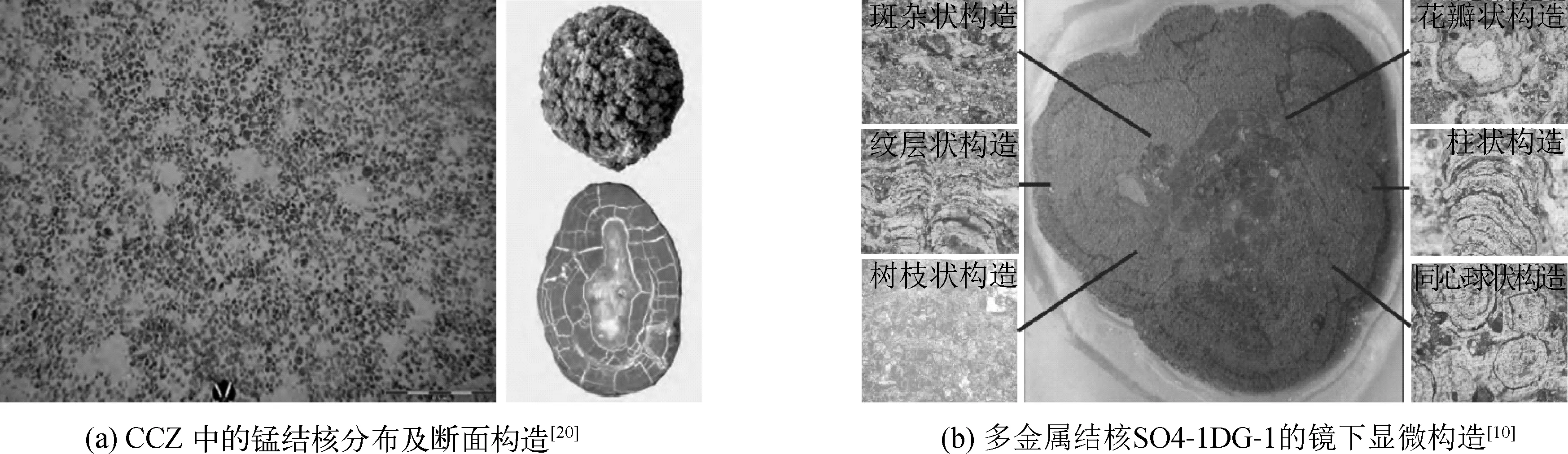


1.2 结核生长速率模型

1.3 结核生长数值模拟方法

2 结果与讨论
2.1 核心物质形状对结核形貌的影响



2.2 多阶段生长模拟




2.3 颗粒在海床静置状态对生长形态的影响

3 结 语

