基于康达效应的海底集矿装置流场与集矿特性试验研究

胡经朝，赵国成，肖龙飞

(1.上海交通大学 海洋工程国家重点实验室，上海 200240; 2.上海交通大学 三亚崖州湾深海科技研究院，海南 三亚 572024)

为缓解陆地矿产资源供需矛盾，世界各国纷纷将目光投向深海矿产的勘探开发[1]。目前，具有商业开采价值的深海矿产主要包括多金属结核、富钴结壳和硫化物[2]。其中多金属结核因富含锰、钴、镍、铜等金属元素，且具有分布广、丰度高、储量大等特点, 而具有较高的开采价值[1]。

目前，开采多金属结核的深海采矿系统主要包括水面支持系统、水力提升系统、中继舱和海底集矿系统。其中，海底集矿系统在海床沉积物表面作业，直接影响矿石采集率、海床冲刷深度等性能指标，最为关键[1]。合理设计的集矿头可在实现高采集率的同时，将对海底环境的扰动降低到最小[3-5]。将多金属结核从海床表面剥离的方法主要有4种：机械采掘式、轴流泵吸扬式、双排喷嘴射流冲采式和基于康达效应的附壁射流吸入式[6]。后三者为水力式集矿方法，相比于机械式具有可靠性高、环境影响小等优点。

对轴流泵吸扬式集矿，赵国成等[7-9]通过模型试验和量纲分析，得到了圆球、椭球颗粒受力系数与离底高度、颗粒偏移角和集矿管水平移动速度的关系。对双排喷嘴射流冲采式集矿，Hong等[10]在二维水槽中对双排射流冲采式集矿方法进行试验研究，得到颗粒采集率与射流流量、集矿头移动速度、离底高度等参数的关系，分析了底面压力分布对矿粒采集率的影响。基于康达效应的附壁射流吸入式集矿，通过向凸曲面壁施加高速切向射流，在近壁面形成高速低压区域，利用速度梯度产生的压力差形成矿粒提升力。该方法可避免水射流对海底沉积物的直接冲击，从而降低集矿过程对海底环境的扰动，最早被日本研制的深海集矿机所采用[11]。Yue等[12]对包含康达效应集矿头在内的3种水力集矿头的集矿性能进行了数值计算和性能比较，发现康达效应集矿头在保证较小环境扰动的同时能保持较高的采集效率；Hu等[13]对抽吸效应和康达效应两种水力式集矿方法进行了试验研究，利用PIV获得了流场云图与速度矢量分布；Cho等[14]对康达效应集矿头开展试验研究，指出射流喷嘴宽度、射流流量、凸曲面壁半径、离底高度是影响矿粒采集率的主要参数；Kim等[15]提出了基于可靠性分析的集矿头性能评价方法，并通过理论计算分析了康达效应集矿头在作业工况下的可靠性。虽然目前已有不少对康达效应水力集矿方法的数值和理论研究，但对真实康达效应流场的分布和颗粒物运动等方面的试验研究相对较少。目前的集矿头测试多偏工程，很少有在实验室对集矿头模型进行集矿性能测试的方法被公开提出。

基于康达效应的水力集矿方法具有结构简单、可靠性高及对海床表面扰动小等优点。因此针对康达效应集矿头，捕捉矿粒在流场中的运动轨迹，利用图像处理获取颗粒运动速度，并基于粒子图像测速(PIV)技术测得集矿流场中的流速分布，研究不同射流流量对矿粒采集率的影响，提出了一系列用于研究集矿头集矿性能的试验方法，为揭示水力集矿机制、优化设计集矿装置提供参考。这些方法对基于其他原理的集矿头模型依然具有相当的应用价值。

1 研究问题描述

法国工程师亨利·康达发现，具有一定速度的附壁射流具有紧贴小曲率壁面流动的趋势[16]。该现象被命名为康达效应，其原理如图1所示。图1中，Q、R分别为附壁射流流量和曲面壁的曲率半径，以曲面壁表面某一点为原点，切向于曲面壁为ζ轴，法向为ξ轴建立坐标系，其中vm为ξ轴上流体质点的速度最大值。大部分动量集中在射流半宽度范围b内，在ξ=b的位置，流体质点速度v=1/2vm。

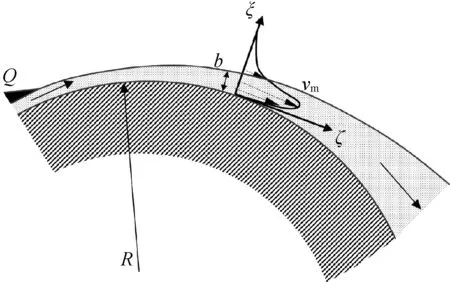
图1 康达效应原理

Kim等[15]认为集矿头射流喷嘴宽度w、曲壁曲率半径R、集矿头离底高度h等参数是影响集矿性能的主要参数，提出基于可靠性设计的优化方法；GSR环境评价报告给出了一种基于康达效应集矿头的几何结构并对其集矿性能进行数值仿真[17]。在此基础上，文中设计康达效应集矿头模型几何结构如图2所示，其中几何参数列于表1。

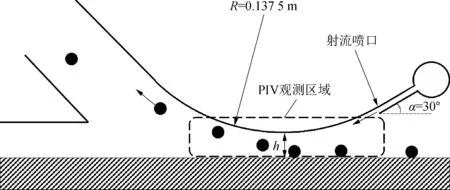
图2 康达效应集矿头模型剖面结构

表1 集矿头主要参数定义

采用3D打印技术制作基于康达效应的水力集矿头模型，材料为光敏树脂。集矿头射流喷嘴形状为矩形，尺寸为0.3 m×0.002 m，射流方向与凸曲面壁相切，并与水平面成30°倾斜，凸曲面壁附近为PIV测量区域。布置在水下的集矿头模型如图3所示，以凸曲面壁最低点为原点，水平向左为x轴正方向，竖直向上为z轴正方向。

图3 集矿头模型照片

2 试验设计

集矿性能试验系统布置如图4所示，包括高透明低铁玻璃水槽[尺寸为2.5 m×1.5 m×1 m(长×宽×高)]、康达效应集矿头、水泵、电磁流量计、PIV测量系统、矿物颗粒等。由水泵驱动的流体经过电磁流量计、限流阀，最终经康达效应集矿头的射流喷嘴沿凸曲面壁切向射出，形成附壁射流，从而产生基于康达效应的集矿流场。试验中，在足够远离集矿头且未到达水槽壁面的位置处的流速已经接近于0，因此认为水槽的边界效应不会对试验结果产生较大的影响。多金属结核模型简化为密度2 430 kg/m3、直径20 mm的黑色玻璃球。

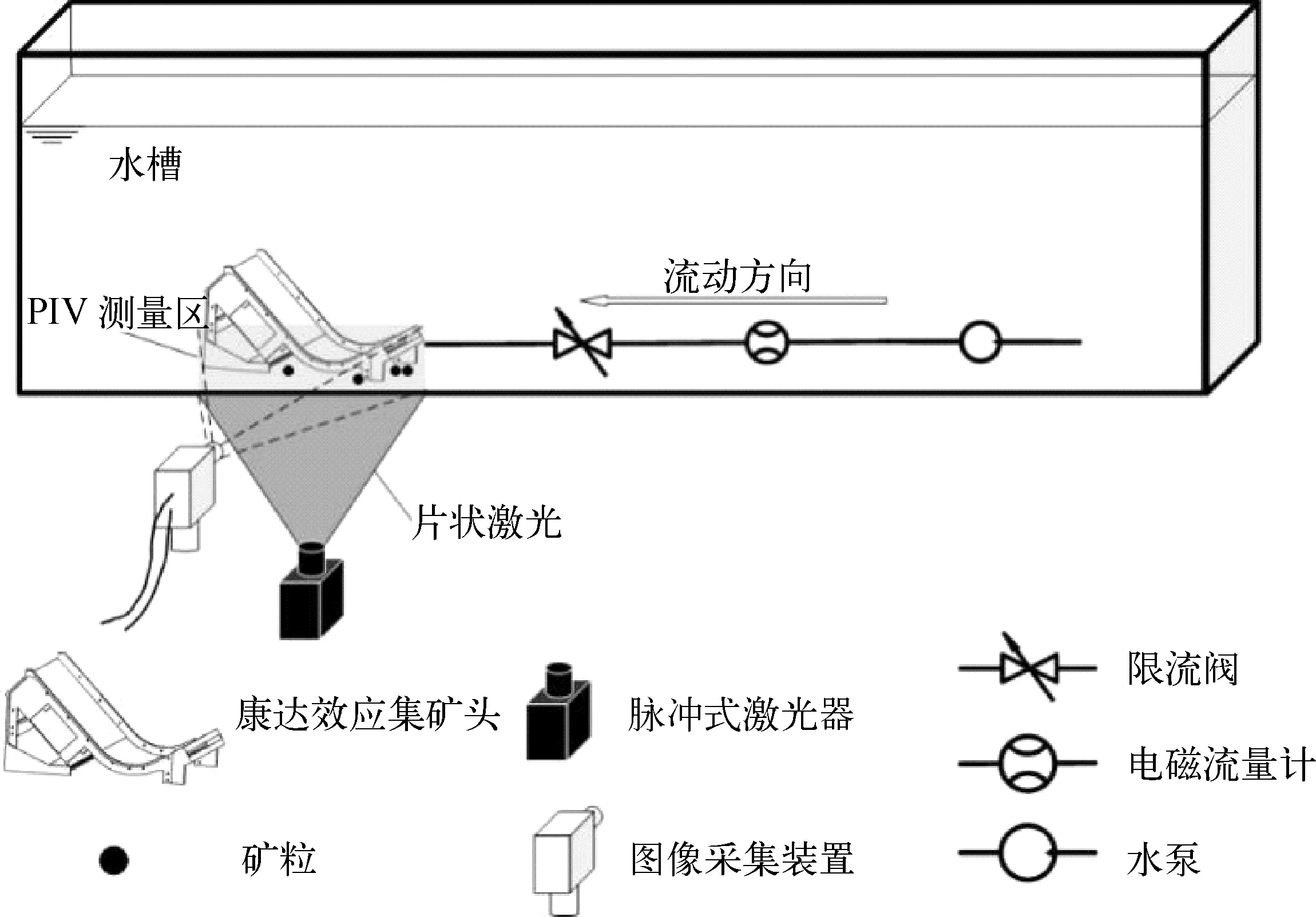
图4 试验系统示意

3类试验工况如表2所示。为获得集矿流场中的流速分布，设计第Ⅰ类试验(PIV流场测量)，测得流量为5.16×10-3m3/s条件下，集矿流场的速度分布；为获得集矿过程中颗粒的运动特性，设计第Ⅱ类试验(颗粒轨迹捕获)，捕捉5种流量下单颗粒在流场中的运动轨迹并对其速度变化进行分析；为获得Q对集矿头集矿能力的影响，设计了第Ⅲ类试验(采集率测量)，获得了12种不同射流流量下的矿粒采集率。

表2 试验类别与工况

3 试验结果与分析

3.1 集矿流场分布

PIV测量得到的集矿流场速度分布及流线图如图5所示(示踪粒子粒径为10 μm)。沿凸曲面壁切向射出的流体质点贴靠凸曲面壁流动，流线平滑，流体质点在靠近凸曲面壁处流速大且沿法线方向速度变化大，而在较远处呈现相反的规律。在x=-30 mm处，流体质点速度达到最大值v=7.1 m/s。

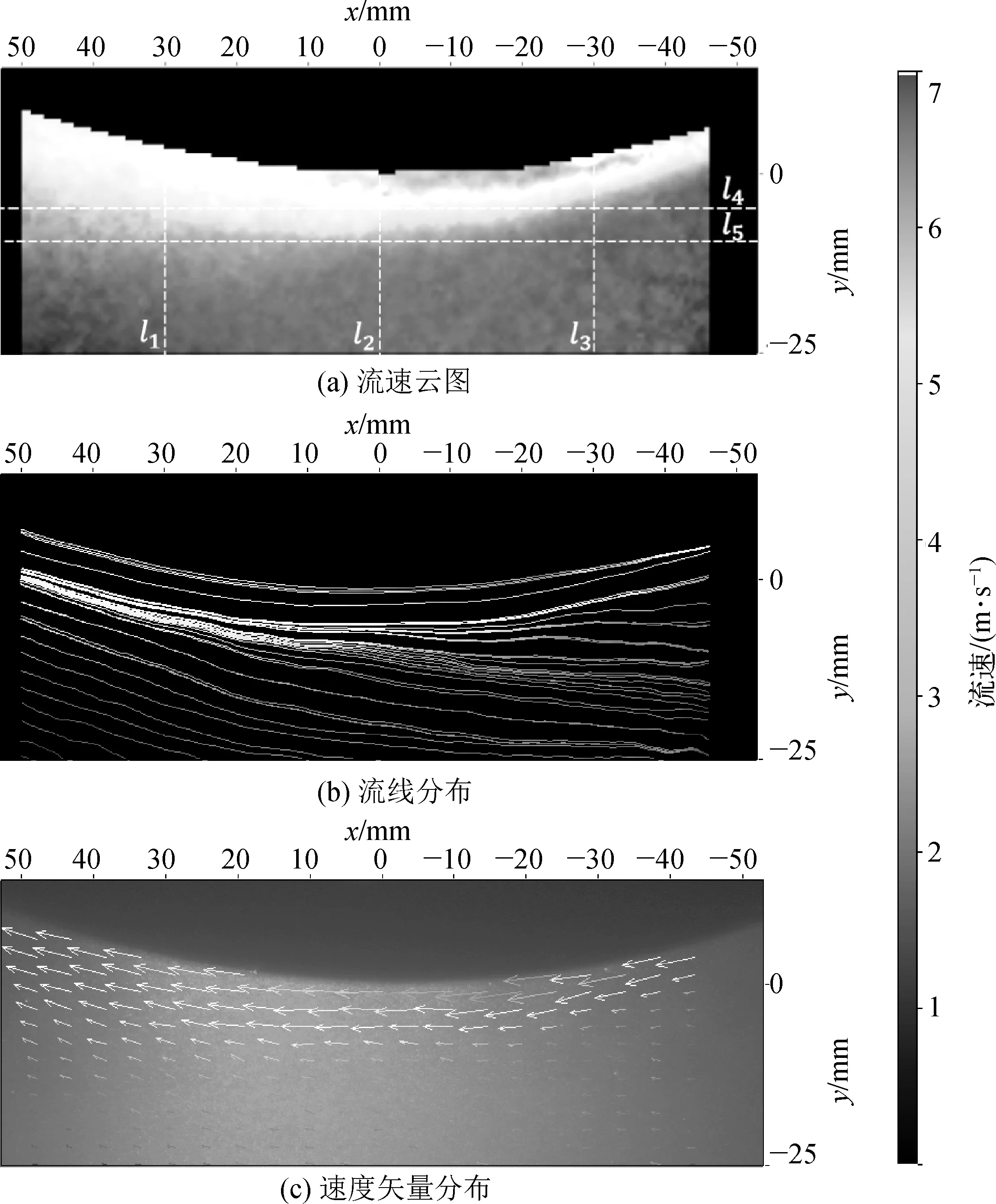
图5 基于PIV技术的流场测量结果

为定量分析集矿流场速度分布特征，选取图5(a)中3条纵向(l1、l2、l3)、2条横向(l4、l5)监测线，分别位于x=30 mm、0、-30 mm，z=-5 mm、-10 mm位置，得到图6所示的各监测线上的流体质点速度幅值分布。由图6(a)可见，在3条竖直监测线上，流体质点的速度幅值随其到凸曲面壁的垂向距离|z|增大而减小。值得注意的是，l1、l2、l3与射流喷嘴的距离依次减小，而|z|-v曲线斜率的绝对值依次减小，这表明越靠近喷嘴的位置速度梯度越大。图6(b)所示为水平检测线(l4、l5)处流体质点的速度幅值分布，其中l4上的流体质点速度幅值随x的增加先增大后减小，在x=-8 mm处达到最大值v=3.1 m/s，并与l5上相同x处的流体质点速度差值达到最大。

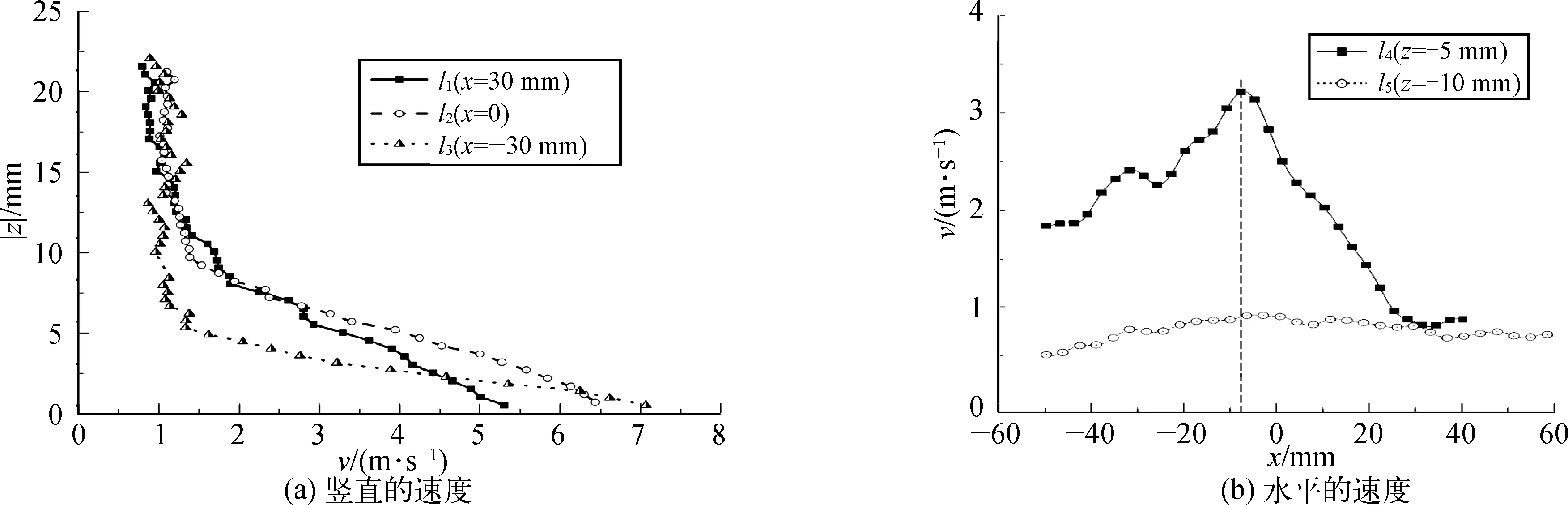
图6 流体质点沿竖直和水平监测线的速度幅值变化

3.2 颗粒运动轨迹

使用高速摄像机捕捉矿粒运动轨迹，并通过图像处理获得运动速度。选取5种(2.39×10-3m3/s≤Q≤5.53×10-3m3/s)不同大小射流流量进行试验，发现在3组较大流量的工况中，颗粒有较大概率被提升至集矿头内，而在另外两种流量下，颗粒被采集的概率较低。因此，选取较大流量下颗粒被采集的运动轨迹和较小流量下颗粒未能被采集的片段作为各流量下的典型运动形态进行分析。

随着流量Q不断增加，试验中可见颗粒呈现出5种典型运动形态，如图7所示。

图7 颗粒运动轨迹

图7(a)为Q=2.39×10-3m3/s时的颗粒轨迹形态，颗粒在离开底面少量距离后，因受到的垂向提升力不足又回落到底面并穿过集矿头，未被采集；图7(b)为Q=3.11×10-3m3/s时的颗粒轨迹，可以看到颗粒在凸曲面壁最低点附近起动，在与集矿头碰撞后回落到底面，仍未被采集；图7(c)所示的颗粒在集矿过程中未与集矿头凸曲面壁碰撞，并被成功采集；图7(d)和7(e)中，颗粒在较大的射流流量作用下被成功采集，但在起动过程中与凸曲面壁发生碰撞。通过分析这5种颗粒运动轨迹形态，发现Q的增加不仅会决定颗粒是否能够被采集，还会影响颗粒的运动轨迹形态。在合适的射流流量Q下，颗粒可以在无碰撞下被成功采集，从而避免可能因碰撞导致的颗粒轨迹交错、采集率下降、集矿头堵塞、凸曲面壁结构受损等情况发生。

颗粒在集矿过程中的运动速度变化如图8所示。随着Q的增大，颗粒水平运动速度Vx和垂向运动速度Vz的最大值均有增大的趋势。颗粒均以约0.45 m/s的速度水平进入集矿流场，然后水平速度快速增大。垂向运动速度反映出不同流量下颗粒起动快慢的不同，在Q较大的两个工况中(Q=5.53×10-3m3/s和Q=5.39×10-3m3/s)，颗粒垂向起动相比于其他3种较小流量工况中颗粒的起动提前发生0.1～0.2 s，颗粒临界垂向起动位置也更靠近布置于集矿头前缘的射流喷嘴处。

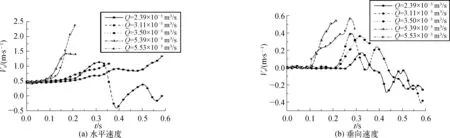
图8 5种不同流量下颗粒运动速度随时间变化曲线

3.3 采集率—射流流量曲线

为得到流量Q对颗粒采集率η的影响，试验测得2.39×10-3～5.53×10-3m3/s共12种不同射流流量下η的变化。在每个流量Q下，从滑道相同高度处释放100个直径20 mm的黑色颗粒，使其带一定初速度进入集矿头底部并记录集矿头采集到的颗粒数量，结果如图9所示。

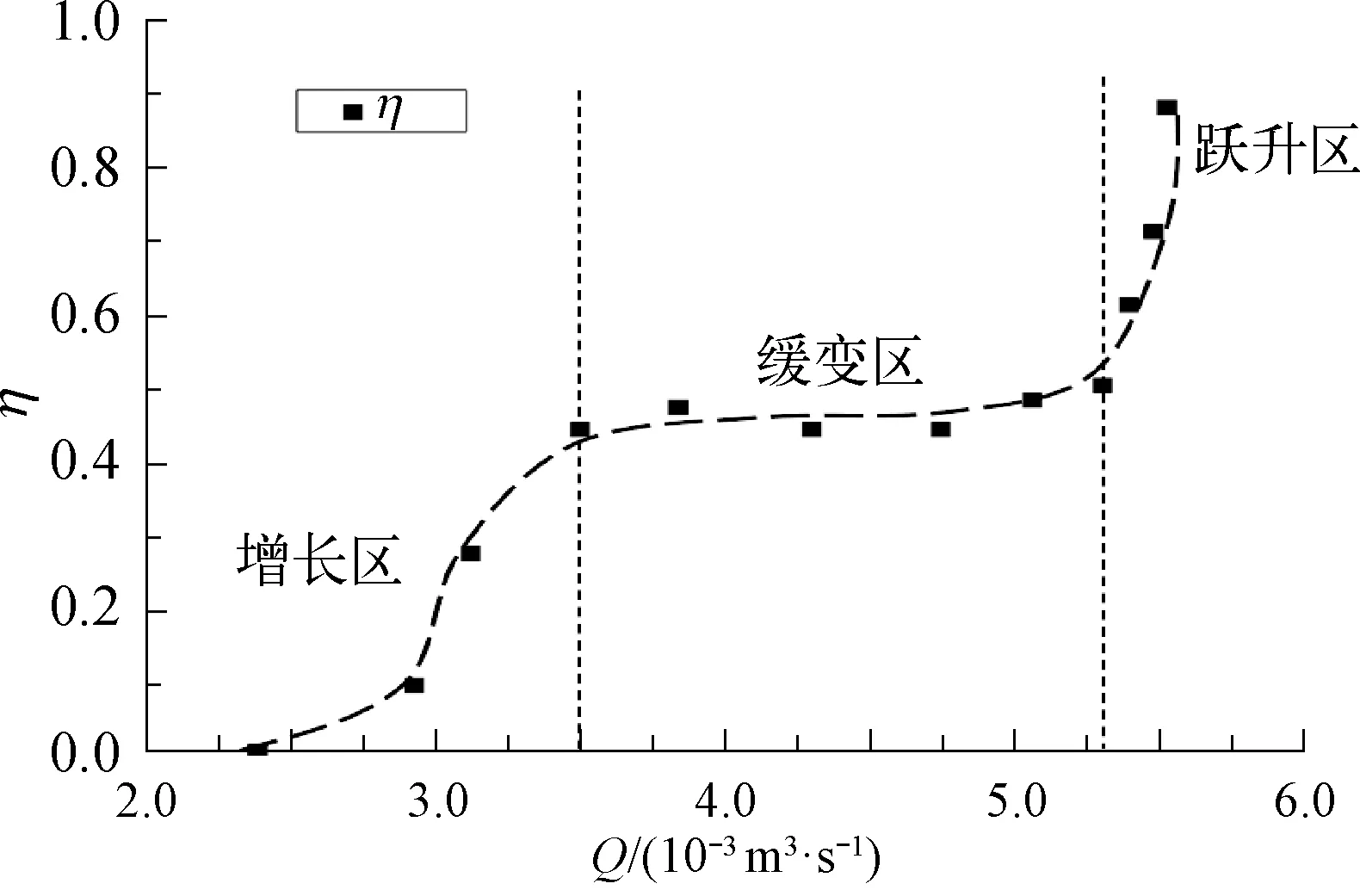
图9 不同流量Q对采集率η的影响

试验表明，当流量过小，即Q≤2.39×10-3m3/s时，颗粒采集率接近于0；当2.39×10-3m3/s

4 结 语

研究探索了康达效应集矿头的研究方法，利用多种方法直观反映了康达效应集矿头的集矿表现，得到结论如下：

1)通过PIV测量得到集矿流场速度分布，发现流线层次分明无大尺度漩涡，靠近壁面处的流速和速度梯度均较大，远离凸曲面壁则流速小且幅值变化不明显。

2)在试验中采用高速摄像和图像识别技术，可准确跟踪测量颗粒运动轨迹和速度。随着流量增大，颗粒运动速度增大，起动位置提前，当流量Q较大时，颗粒将会更快起动并在集矿流场的作用下得到提升。

3)随着射流喷嘴流量增大，颗粒采集率变化可划分为增长区、缓变区和跃升区，分别在流量为2.39×10-3～3.50×10-3m3/s范围随流量增大近似线性增加，在流量为3.50×10-3～5.31×10-3m3/s时保持稳定，采集率为约45%，在流量为5.31×10-3～5.53×10-3m3/s时随流量增大而急剧上升，最终采集率接近90%。值得注意的是，若考虑真实集矿环境底质的存在，不同采集率所对应的流量范围将发生变化。

未来的集矿头设计将尽最大可能遵循BAT原则[18-19]，即“best available technology”，这对集矿头的集矿性能提出了综合性的要求，即在保证尽可能小的环境扰动的同时，将采集率维持在一个较高水平。采集率指标与集矿头本身的各项参数密切相关，例如曲面壁曲率、射流流量、射流喷嘴倾斜角度、集矿高度等参数都有可能对集矿表现产生较大影响。研究可加深对基于康达效应集矿机制的理解，丰富水力集矿试验方法，并为水力集矿头的优化设计及集矿系统动力参数选取提供参考。