吸引与排斥耦合神经元中的稳定幅度奇异态
刘维清,彭玉祥
(江西理工大学理学院,江西 赣州 341000)
0 引言
在人脑中大量神经元通过相互作用产生丰富的自组织动力学行为,如各种形式的同步[1-2]和时空斑图[3-4]等.其中同步[5-6]是指原本具有不同频率的振子在一定强度的相互耦合作用下趋于相同频率的振荡的现象.在达到同步之前,耦合振子会分化成部分同步振子(相位相关)与不同步振子(相位不相关)在空间上分区共存的现象,被称为奇异态.因其与人脑工作记忆和半脑睡眠现象[7-8]密切相关而倍受人们的关注.由于奇异态的吸引域较小,且其存在时间随系统的尺寸增加而呈指数级增加,所以它常被认为是在系统走向同步过程中的过渡态.在Abrams等利用OA理论确定了奇异态的稳定性条件后,人们在神经元系统[9]、化学系统[10]、光学系统[11-12]、机械系统、电子系统[13-14]等中均观察到了这一现象.通常信号包括相位和振幅信息,除了上述相位的空间相关与不相关共存产生的奇异态外,人们还发现在耦合系统中幅度和相位均具有空间相关和不相关共存的态,被称为幅度奇异态[15-16].此外,人们进一步观察到只有幅度的空间相关和不相关共存的幅度奇异态[17].幅度奇异态与初始条件密切相关,且由于其为走向完全同步过程的过渡态,因此幅度奇异态较难被观察到.通过在耦合中引入时间延迟或在噪声影响下,幅度奇异态的暂态时间可以延长.如何得到稳定的幅度奇异态一直是人们关注的问题.文献[18]通过引入虚数参量,在耦合极限环振子中可以得到稳定的幅度奇异态.在耦合混沌振子系统中通过引入排斥耦合作用[19],可以得到多团簇的幅度奇异态,且随着排斥耦合作用的增加,耦合振子系统进一步走向死亡奇异态[20-21].虽然在耦合振子系统模型中可以得到稳定的幅度奇异态,但在实际耦合神经元中是否可以得到稳定的幅度奇异态仍不清楚.为了弄清这一问题,本文以耦合FHN神经元振子系统为模型,引入旋转耦合方式[22],研究幅度奇异态的产生条件和参数区间.结果表明:当旋转耦合角约为π时,在神经元振子激活变量和抑制变量耦合中引入吸引与排斥耦合作用竞争,可以得到稳定的相位奇异态、幅度奇异态和死亡奇异态.奇异态的团簇数量与耦合作用半径呈幂律相关.通过对2个耦合FHN振子模型分析,发现在稳定的幅度奇异态的产生与吸引与排斥耦合作用的竞争下通过霍普夫分岔产生新频率的振荡相关.在耦合作用下新频率的振荡态最终走向振荡死亡态而进一步产生死亡奇异态.
1 耦合FHN振子模型
以N(N=1 000)个1维非局域环形耦合FHN振子系统为模型,
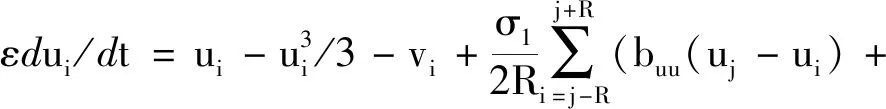
(1)
其中ui、vi(i=1,2,…,N)分别为神经元的激活变量和抑制变量,即快变量和慢变量.ε是快变量和慢变量的时间尺度比值,为一个正的小量,本文固定ε=0.05;ai表示系统的控制参数,决定着在整个系统中振子的动力学特征.当|ai|<1时,系统为振荡态,否则为可激发态.本文以振荡态的神经元振子为研究对象(即取ai=0.5).σ1、σ2分别为激活变量方程和抑制变量方程的耦合强度,R决定着耦合作用半径r(r=R/N).旋转耦合矩阵[22]可表示为
(2)
其中相位φ∈[-π,π]控制着激活变量和抑制变量之间耦合作用的竞争关系.当φ=π/2[23]时,buv=1,bvu=-1,buu=bvv=0,激活变量负反馈σ1(uj-ui)作用在抑制变量方程上,而抑制变量负反馈σ2(vj-vi)作用在激活变量方程上.此时,随着耦合强度σ1、σ2的增加,耦合系统会产生稳定的多团簇相位奇异态[20].当φ=π时,buv=bvu=0,buu=bvv=-1,激活变量负反馈σ1(uj-ui)和抑制变量负反馈σ2(vj-vi)分别作用在激活变量方程和抑制变量方程上.当σ1>0时,激活变量为排斥耦合作用,当σ2<0时,抑制变量为吸引耦合作用.当φ∈[π/2,π]时,激活变量负反馈σ1(uj-ui)和抑制变量负反馈σ2(vj-vi)按一定权重分别作用在2个变量u、v的方程上.当φ=π-0.1时,耦合振子系统的斑图结构,即通过引入少量的交叉变量耦合作用,发现:当σ1>0且σ2<0时,耦合振子系统在排斥与吸引耦合竞争作用下产生丰富的动力学行为,包括稳定的幅度奇异态和死亡奇异态.
2 仿真与结果
为了探讨获得稳定幅度奇异态的条件,取φ=π-0.1,耦合半径r=0.38,并固定耦合强度σ1=0.28,分析耦合强度σ2的变化对耦合振子系统动力学行为的影响.对方程(1)使用4阶Runge-Kutta法进行数值求解.ui和vi的初始条件随机分布在半径为2的圆上,即uk(0)2+vk(0)2=4.当σ2>0时,随着耦合强度σ2的增加,耦合振子系统表现为行波态,图1(a)为当σ2=0.5时激活变量u的时空斑图,其中色条表示激活变量u的值.对应的图1(e)为所有振子的激发变量ui在某一时刻处的取值的空间分布.而当σ2<0时,耦合振子系统表现出丰富的动力学斑图,如当σ2=-0.7时,可以观察到稳定的4团簇相位奇异态(见图1(b)、图1(f)).当σ2=-1.0时,耦合振子系统变成4团簇幅度奇异态(见图1(c)、图1(g)).由激活变量u的空间分布可知,大振幅振荡振子将分别为正值和负值的2个小振幅振荡区域分隔开.若继续增加σ2的绝对值,则在稳定幅度奇异态中大振幅的振子会逐渐合并到小振幅区域,同时小振幅振荡的振幅逐渐减小直至变成稳定固定点,从而产生死亡奇异态.图1(d)、图1(h)为当σ2=-1.2时耦合振子系统处于4团簇死亡奇异态的时空斑图和对应的某一时刻激活变量的空间分布图.此时耦合振子为正的固定点区域和耦合振子为负的固定点区域交替组成.
耦合振子的奇异态的特征受耦合作用半径r的影响.为了进一步确定耦合作用半径r影响耦合振子系统幅度奇异态的特点,得到当σ1=0.28,σ2=-1.0且耦合作用半径分别为r=0.001、0.050、0.200、0.400时耦合系统的时空斑图和对应的激活变量在某一时刻处的空间分布图.在r=0.001(即R=1)时,耦合振子系统的激活变量u分别处于正的小幅振荡态和负的小幅振荡态及少量大振幅振荡态(见图2(a)、图2(e)).当r=0.050时,在耦合振子中正的小振幅振荡区域和负的小振幅振荡区域均扩大,且它们之间被大振幅的振子区域分隔.此时,幅度奇异态的团簇数减小为28个(见图2(b)、图2(f)).当r=0.200时,在耦合振子中正的小振幅振荡区域和负的小振幅振荡区域进一步扩大,幅度奇异态的团簇数减小为8个(见图2(c)、图2(g)).当r=0.400时,幅度奇异态的团簇数减小为4个,如图2(d)、图2(h)所示.因此,随着耦合作用半径r的增加,幅度奇异态的团簇数量逐渐减小.

图1 当固定σ1=0.28,σ2=0.5、-0.7、-1.0、-1.2时耦合振子系统的时空斑图和某时刻激活变量的空间分布图
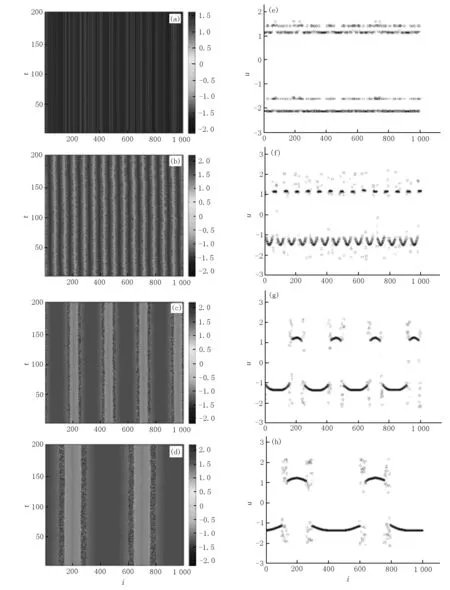
图2 当r=0.001、0.500、0.200、0.400时耦合振子系统的变量u的时空斑图和某时刻激活变量的空间分布图
为了进一步确定耦合作用半径r对幅度奇异态和死亡奇异态的定量关系,图3给出了幅度奇异态或死亡奇异态的空间相关区的团簇数量Nc与耦合作用半径r的关系图(其中图内插图为取双对数坐标的结果).研究结果表明:幅度奇异态和死亡奇异态的空间相关区的团簇数量Nc均与耦合作用半径呈幂律关系,即Nc∝αr-γ,其中α=1.72,γ=-0.925.
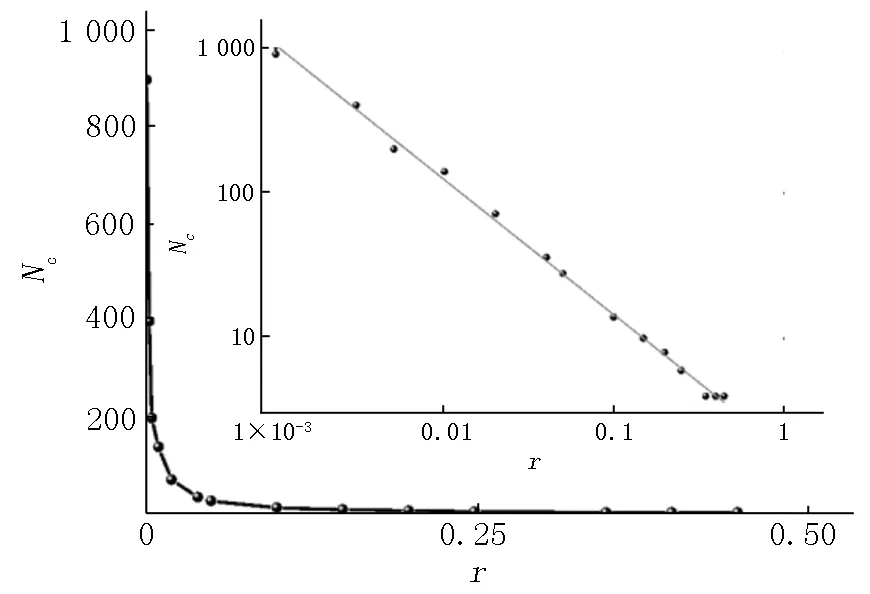
图3 当σ1=0.28,σ2=-1.0时,团簇数量Nc与耦合半径r的关系图
3 机理分析
为了更好地理解幅度奇异态产生的机制,以2个耦合FHN的动力学为例.
dv1/dt=u1+a1+σ2(bvu(u2-u1)+bvv(v2-v1)),
dv2/dt=u2+a2+σ2(bvu(u1-u2)+bvv(v1-v2)),
其中旋转耦合矩阵与式(2)相同,方程参数与式(1)相同,φ=π-0.01,固定σ1=4,当σ2≥0时,耦合振子处于反相同步大振幅振荡态,这2个振子之间保持平移对称性(见图4(a)、图4(e)(σ2=0)).而当σ2<0时,随着耦合强度绝对值的增加,耦合振子仍保持平移对称性,振荡的周期逐渐变大.同时,在时序的平台处(见图4(b)中HB所指示处)产生霍普夫分岔而产生新的频率成分的振荡(见图4(b)、图4(f)(σ2=-1.20)),这一现象因在心肌细胞[24]中出现而被称为心肌细胞的早期后除极现象,是心律失常的内在机制.而当耦合强度再增加时,新的频率成分的振荡会取代原有的大周期振荡.值得注意的是,具有新频率的2个振子的吸引子分别处于2个不同的旋转中心,且其吸引子一大一小,出现平移对称性破缺(见图4(c)、图4(g)(σ2=-1.21)).在R近邻耦合作用下,当吸引与排斥耦合作用竞争时,处于相同(正或负)旋转中心的吸引子形成空间相关性,而处于正、负空间相关态之间的振子在它们竞争作用下表现为大振幅振荡态而形成空间非相关态.显然,耦合引起的平移对称性破缺而形成的2个不等大的小振幅振荡与原有的大振幅振荡的竞争是产生稳定幅度奇异态的主要机制.耦合强度进一步增加,新频率成分的振荡幅度减小并最终走向一正一负的振荡死亡态(见图4(d)、图4(h)(σ2=-1.40)).当耦合作用半径增加时,这2个振荡死亡态在耦合作用下相互竞争而形成死亡奇异态.
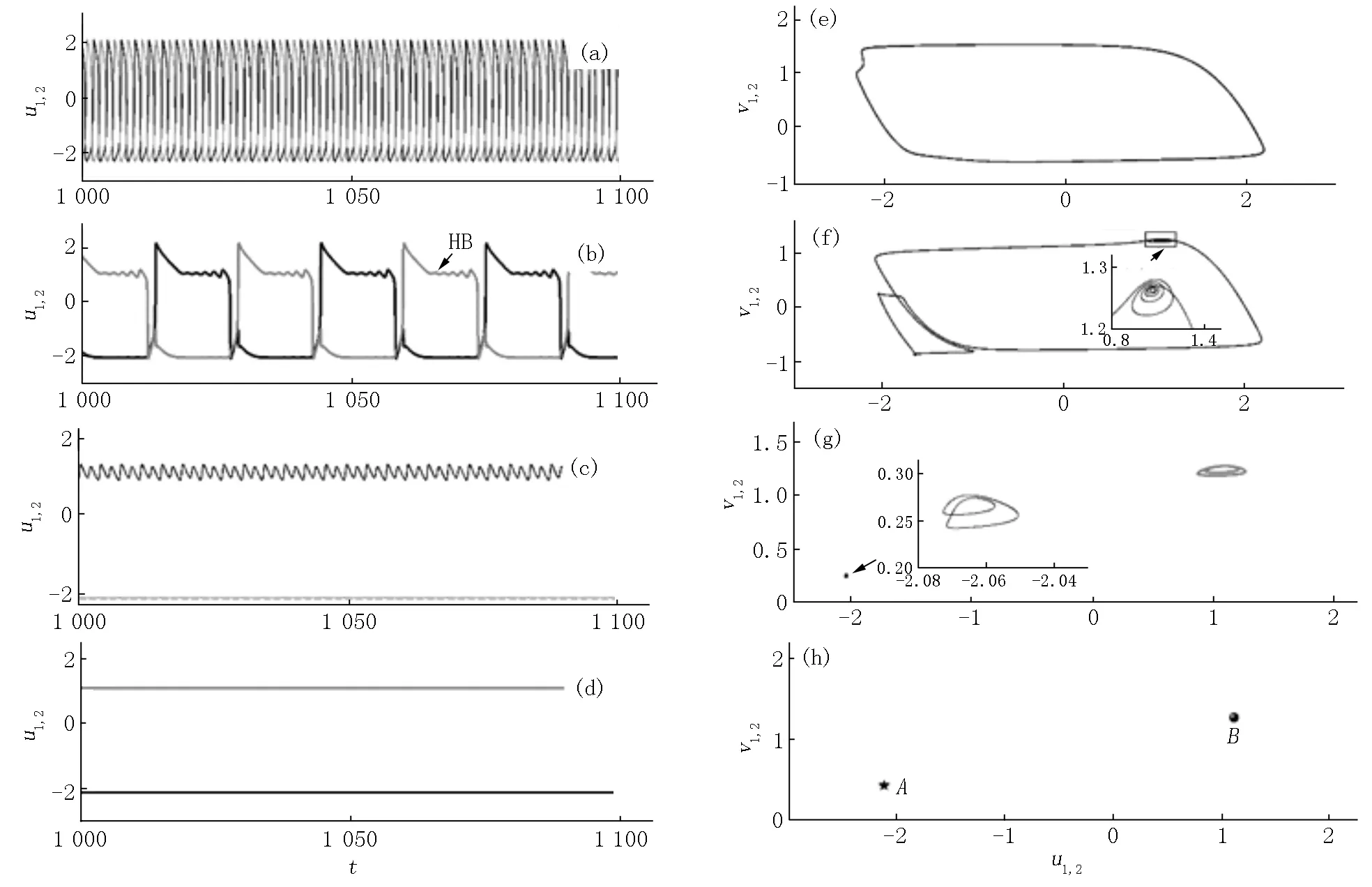
图4 当σ2=0、 -1.20、-1.21、-1.40时,激活变量u的时序和神经元振子的相图
4 结论
在耦合FHN神经元振子系统中引入激活变量和抑制变量的负反馈耦合作用,并在吸引与排斥耦合竞争下,耦合振子系统会随着吸引耦合作用的增加而从相位奇异态走向稳定的幅度奇异态,最后走向死亡奇异态.随着耦合作用半径的增加,奇异态的团簇数量会随耦合作用半径增加而呈幂律关系减小.通过2个耦合FHN振子模型分析确定了稳定幅度奇异态产生的机制是在耦合作用下通过霍普夫分岔产生一对振荡中心分别为正值和负值的小振幅振荡,且新产生的振荡与原有的大振幅的振荡竞争而形成稳定的幅度奇异态.随着耦合强度进一步增加,新频率的振荡振幅减小到0而形成一正一负的振荡死亡态,当耦合半径增加时一正一负的振荡死亡态竞争而形成死亡奇异态.对神经元振子系统在吸引与排斥耦合竞争下形成的稳定的幅度奇异态和死亡奇异态的机制的分析为理解人脑功能提供理论支持.

