干湿循环作用下边坡动力稳定性的试验研究和数值模拟

靳云龙

(中冀建勘集团有限公司，河北 石家庄 050227)

0 引言

边坡的失稳往往伴随着强降水(如暴雨)的发生，针对降水导致边坡失稳问题，众多学者进行了一系列试验研究和数值计算。聂兵其[1]针对水库边坡，基于GeoStudio软件的极限平衡分析法对关键参数进行了敏感性分析，发现土的内摩擦角和粘聚力对其稳定性影响最大。熊俊[2]利用模型箱试验模拟含水边坡，对参数识别方法进行了优化。夏良等人[3]通过断裂力学理论推导了边坡在裂缝充水条件下的深度临界公式，研究结果表明，边坡失稳的关键因素是内水压力突然升高。张家俊[4]针对干湿循环作用下的膨胀土边坡，进行了室内实验研究，对裂隙度演化规律进行了分析。

近年来，边坡和挡墙在地震荷载作用下的力学性能也一直是研究的焦点。陈冲[5]在此基础上，考虑到了地震加速的的影响，结合FLAD(3D)强度折减法对边坡浸润面位置进行了研究。黄凤娟[6]通过PLFC2D软件，利用有限拆分法结合实际工程案例给出了地震作用下边坡稳定性的数值解。张进忠[7]等人利用极限概率法，对地震作用下的边坡进行了不确定性分析，对临界抗力进行了计算。杨兵[8]分析了为了探讨堆积体边坡在地震作用下的失稳特征及动力响应特性，对无量纲地震加速度幅值和频率参数的规律进行了研究，并对堆积体边坡进行了稳定计算和参数分析。

为研究干湿循环作用下边坡的稳定性，本文利用试验和数值模拟两种手段，通过动三轴试验系统进行了16组试验来分析边坡三向应力状态，对土体动力特性进行研究。利用有限元软件建立了涉水超高边坡模型，对在干湿循环和地震双重作用下的边坡力学特性进行了分析，并基于强度折减法对边坡进行稳定性分析，计算安全系数。

1 动静三轴试验

1.1 实验设备

实验设备采用实验室标准动静三轴试验伺服系统，该设备可设置不同周围压力，通过轴向加载和应力、应变两种控制方式。可设置0～5 Hz范围频率进行动力加载。实验设备如图1所示。

图1 三轴仪器实物图

1.2 试样制备

试验采用常规黄黏土，取样深度10 m左右，通过筛分法进行了颗粒筛分得到颗粒级配曲线。小于2 mm土样粒径的颗粒含量占比为94.5%，小于0.075 mm土样粒径的颗粒级配含量为81%。其他物理性质见表1。试验时进行饱和，饱和含水率约为37%。三轴实验试样尺寸为60 mm×120 mm。

1.3 试验方案

通过室内试验，对土体多次脱水-浸泡以模拟自然环境下的土体干湿循环。首先，利用35℃的烘箱对饱和土样进行蒸发脱湿，时间为8 h。其次，将土放入蒸馏水中浸泡16h用来模拟水分浸润作用。此两个步骤完成即为一个干湿循环。

本研究共进行了16组试验，试验方案如表2所示。静三轴试验的围压设定为50 kPa、100 kPa和200 kPa三组，分固结试验和排水剪切试验两个步骤，剪切速率均设置为0.01 mm/s。动三轴试验围压逐步增加到300 kPa，然后施加轴向动应力σd，为1 Hz的正弦波。查阅相关文献和规范，设置动应力比为0.5，即轴向动应力为150 kPa，并在实验试测定轴向位移和孔隙水压力。

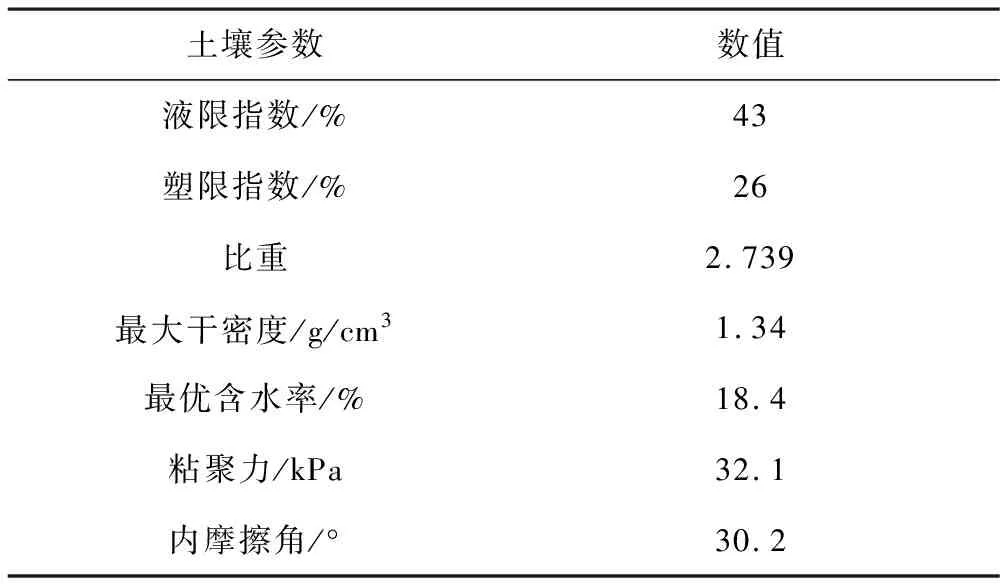
表1 土壤参数

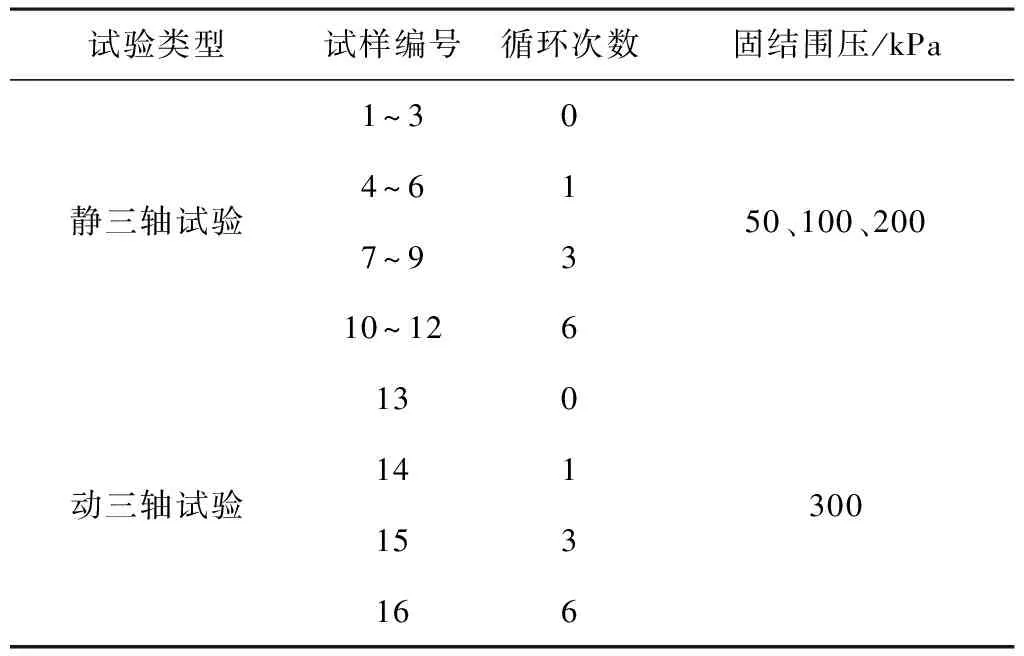
表2 动静三轴试验方案

2 实验结果分析

2.1 静三轴试验

按照表2试验方案，先后进行静三轴中的固结和轴向排水压缩至破坏，得到如表3所示的抗剪强度参数。从图中可以看出，呈现出随着干湿循环次数的增加，土体有效粘聚力逐渐降低趋势，而内摩擦角并没有表现出一定规律性。说明由于干湿循环过程使得土颗粒的胶结作用被降低。

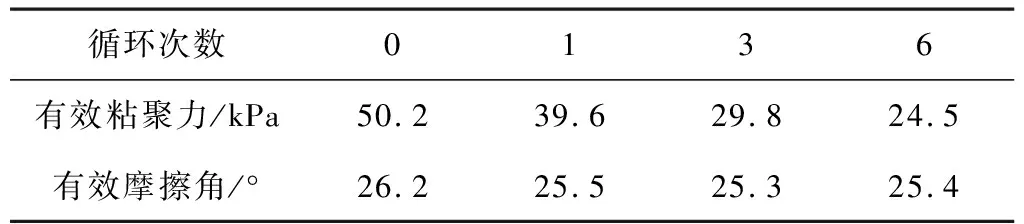
表3 不同干湿循环作用下土样的抗剪强度参数

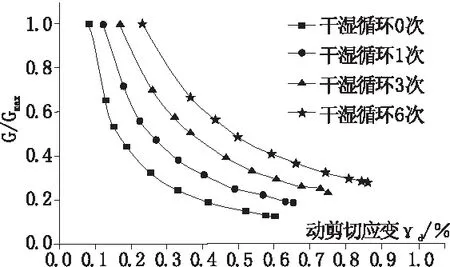
图2 (G/Gmax)-动剪切应变关系曲线

2.2 动三轴试验

为研究动荷载作用下土体的力学特性，进行动三轴试验。定义动剪切应力比值M=τd/σ3，孔隙水压力比值R=μ/σ3，μ为空隙水压，σ3为固结围压。对(G/Gmax)-动剪切应变关系、振动循环数-动剪应力比关系和孔隙水压力比-振动循环数比关系进行了研究。实验结果如图2～图4所示。

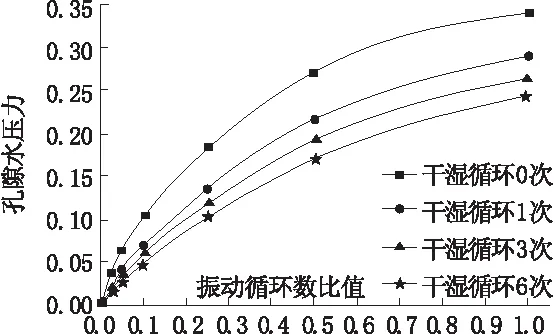
图3 空隙水压力比-振动循环数比关系曲线

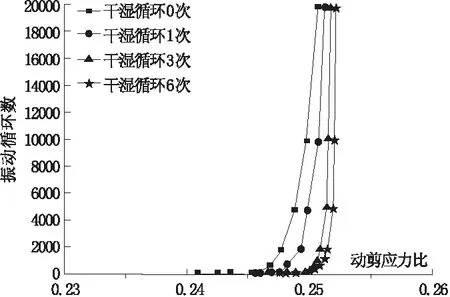
图4 振动循环数-动剪应力比关系曲线

由图2～图4可知，土样干湿循环次数与第一次振动周期造成的变形和完成后剪应变最终值呈正比，循环次数越多，第一次振动周期变形和最终剪应变越大，而孔隙水压力则减小，与孔隙水压力呈反比。此外，动剪切应力比受循环次数影响较为微小，说明动剪切应力直接相关的是初始设定的动应力。

3 边坡稳定性分析

3.1 计算方法

在稳定性分析阶段，参数是由摩擦系数(tanφ)和黏聚力(c)通过将其除以折减系数ΔMsf得到。

(1)

式中：φinput为土的初始摩擦角；φreduced为折减之后土的摩擦角；cinput为土的初始黏聚力；creduced为折减之后土的黏聚力。

将安全系数定义为ΔMsf的值，当连续增量不断减少时，连续ΔMsf之间的差异变得非常小,通过不断迭代的方式获得安全系数。潜在破裂面的找寻是根据节点计算处的集中剪切应变增量。

根据以上试验研究，本文利用岩土有限元分析软件进行边坡有限元计算，并基于强度折减法进行了稳定性分析，计算出了在不同干湿循环条件下边坡的安全系数。材料采用摩尔-库伦模型，各层土材料本构模型及主要参数根据参考文献和相关经验参数确定。模型参数如表4所示。利用该软件自带的动力模式模拟实际工程中主要由地震产生的动力荷载或爆炸产生的冲击波等。

3.2 模型参数

本研究选用的实际工程案例为三峡库区的一个超高涉水边坡，存在碎石堆积体。全部高程121 m，纵向长度约1 500 m。考虑到计算效率，本研究选用平面应变模型模型。网格划分选择局部加密，共划分出19 050个网格，85 642个节点。如图5所示，图5(a)为有限元模型图，图5(b)为生成网格后的节点连接图。

表4 模型计算参数

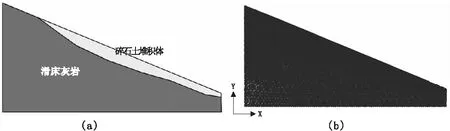
图5 边坡模型

为更好地模拟实际施工条件，观测路基变形，设置边界条件为：边坡四周水平约束，底部固定约束，顶部自由约束。同时为吸收动力荷载所产生的回弹效应，动力边界为黏性。设置边界条件如表5所示。

表5 边界条件

3.3 结果分析

利用有限元软件模拟边坡在干湿循环和地震双重作用下的边坡的力学特性并计算安全系数，共分为三步：

(1)初始步。生成由土体自重产生的初始应力；

(2)塑型计算。基于上步，施加荷载后进行塑形计算，得到应力应变曲线;

(3)稳定性分析。基于有限元强度折减法，通过迭代的方式，计算边坡的安全系数和临界破坏面。

在动荷载作用下，空隙水压力在不同观测点与振动时间关系曲线如图6所示。从图中可以看出，孔隙水压力的递增和重分布在2 s内基本完成，在2～10 s振动区间内孔隙水压基本无变化。边坡观测点D、E、F三点的空隙水压力逐渐增大，说明在动荷载作用下，振动使得水力条件变化，令边坡地下水位上升，孔隙水压力则主要由库水压力产生。D点的空隙水压力增加量最高，为120 kPa，E点的孔隙水压力增加了75 kPa。

计算了在干湿循环和动力荷载作用下的局部边坡安全系数，如表6所示。随着干湿循环次数的增加和施加振动荷载，边坡局部安全系数发生了不同程度的减小，且趋势逐渐变缓。最大减小幅度为20%。这是由于边坡土体受到水压力重分布和动力荷载作用后，边坡土体结构发生改变，应力集中，更容易发生失稳破坏。

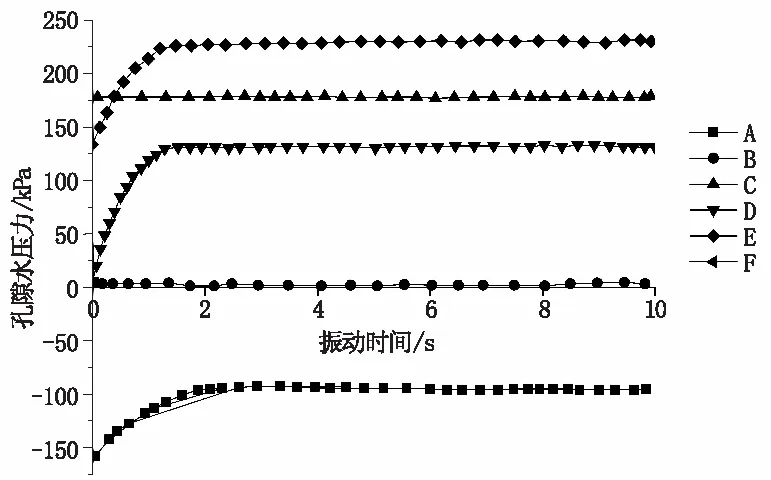
图6 观察点孔隙水压力-振动时间变化曲线

表6 边坡前缘坡脚安全系数

4 结语

根据相关规范，利用动静三轴试验试验研究了在干湿循环作用下边坡土体的剪切和动力特性，基于此，结合工程实例，利用有限元软件建立了涉水超高边坡的有限元计算模型，研究孔隙水压力与振动时间的关系，并进行稳定性分析，计算出了安全系数。主要结论如下：

(1)随着干湿循环次数的增加，土体有效粘聚力逐渐降低趋势，而内摩擦角并没有表现出一定规律性，干湿循环过程使得土颗粒的胶结作用被降低。

(2)干湿循环作用下，会改变土体的动力特性参数，如最终动剪切应变、初始动剪切模量和阻尼比。在动荷载作用下，使得边坡地下水位线升高，导致孔隙水压力重分布，水压力增高。

(3)在干湿循环和动力荷载共同作用下，边坡稳定性系数发生改变。边坡稳定性系数与干湿循环次数呈负相关，最大安全系数降低20%左右。