认知诊断模型参数估计算法比较

汪文义,郑娟娟,宋丽红,胡海洋

(1.江西师范大学计算机信息工程学院,江西 南昌 330022;2.江西师范大学教育学院,江西 南昌 330022)

0 引言

认知诊断评估(cognitive diagnostic assessment)是20世纪中后期兴起的一种新的测验方式,它以心理学、教育学为指导,同时借助现代测量学,对被试答错的项目进行深入分析与解释,能够分析被试对项目所考察的所有知识点(属性)的掌握情况,基于此可以对症下药制定补救措施,加强短板的学习.认知诊断评估通常借助于认知诊断模型(cognitive diagnostic model,CDM),根据设定好的Q矩阵,建立被试的属性掌握情况与项目反应之间的关系[1].

现有的认知诊断模型有100种以上,主要分为简化模型、饱和模型2个大类,其中简化模型又分为补偿模型和非补偿模型,它们的最常用模型分别为DINO模型[2]和DINA模型[3],在饱和模型中最常用的模型为G-DINA模型.然而要想借助于认知诊断模型实现认知诊断,就必然离不开认知诊断模型的参数估计方法,故参数估计对于模型的发展与实现有着非常重要的意义.

J. de la Torre等[4]将马尔可夫链蒙特卡罗方法(Monte Carlo Markov chain,MCMC)用于高阶DINA模型参数估计.J.L. Templin等[2]也将MCMC方法用于DINO模型参数估计.J. de la Torre[3]提出DINA模型EM参数估计算法并考查了EM算法的表现,但没有通过模拟研究去比较EM参数估计算法和MCMC参数估计算法的表现.S. Sen等[5]对可用于DINA模型参数估计(EM方法)的6个软件表现进行比较,结果显示各软件表现基本相当.J. de la Torre[6]提出G-DINA模型及其EM估计算法.有研究将变分贝叶斯推断方法用于DINA模型和G-DINA模型参数估计[7-8].

Zhan Peida等[9]为G-DINA模型(与对数线性认知诊断模型LCDM等价)提供了MCMC估计的JAGS代码.S.A. Culpepper等[10]基于数据扩张的MCMC方法,并采用吉布斯方法对属性条件概率下的知识状态进行取样,用于简化的重新参数化融合模型参数估计,以提高MCMC效率.随后,Wang Juntao等[11]将其推广用于G-DINA模型参数估计,然而也没有与EM算法比较.Jiang Zhehan等[12]还使用MCMC的其他变形形式实现了G-DINA模型的参数估计.

通过对已有文献分析发现,这2类方法各有优劣,如EM算法(或变分法)收敛速度较快,但会受初值影响且可能收敛到局部最优值[8],而MCMC算法比较费时但不依赖于初值.于是,有必要在不同样本量、不同测验长度、不同题目质量的条件组合下,对DINA模型、DINO模型、GDINA模型下的EM算法和MCMC算法的表现进行系统比较.因为认知诊断模型常规的EM算法(非变分法)可借助于各种软件包(如R语言实现的CDM或GDINA)来实现,并且JAGS代码实现认知诊断模型的MCMC十分简单,所以,本文主要考虑在认知诊断中常规的EM算法和JAGS代码实现的MCMC算法,不考虑它们的其他变形方法.在简要介绍了认知诊断模型下的EM算法和MCMC算法后,通过模拟研究,在不同样本量、不同测验长度、不同题目质量的条件组合下,在DINO模型、DINA模型和GDINA模型下比较了EM算法和MCMC算法的表现,可供读者根据不同条件为各个模型选择最适合的参数估计算法.

1 模型与方法

1.1 认知诊断模型

(i)DINA模型.确定性输入噪音与门(DINA)模型是认知诊断中运用最广的模型,同时也是一种完全非补偿的认知诊断模型,它要求被试需掌握项目所考察的所有属性,缺少其中任何一个属性都会降低答对项目的概率[6].DINA模型的项目反应函数为

(ii)DINO模型.确定性输入噪音或门(DINO)模型恰好与DINA模型相反,在该模型中被试只要掌握了项目考察的任何一个属性就能正确答对该项目,即属性间可以相互替代或补偿[7].DINO模型的项目反应函数为

1.2 EM算法

EM算法是一种迭代优化策略,该策略在每次迭代中都分成了2个步骤:第1步是期望步,简称为E步;第2步为极大步,简称为M步.EM算法是数据挖掘经典算法之一,它最初是为了解决在数据缺失情况下进行参数估计的问题而提出的,后来被用于寻找在缺失数据统计模型中参数的最大似然估计或者最大后验估计[9].

1.2.1 DINA、DINO模型的EM算法 通过上述介绍的EM算法,给定知识状态αi,在条件独立假设下(即同一被试对各个项目的作答是相互独立的),被试在M个项目上的得分向量为Xi=(xi1,xi2,…,xiM),在N个被试的作答模式相互独立假设下,得分矩阵X的条件似然函数为

将所有被试看成是来自同一母体,且给定属性掌握模式的先验分布为P(αc),αc∈Qs,其中Qs为知识状态全集,如在含K个属性的独立结构下Qs包含2K列,于是可得边际似然函数(边际分布)为

即在DINA和DINO模型上边际似然函数表示为

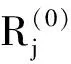
1.2.2 G-DINA模型的EM算法 在G-DINA模型上边际似然函数表示为

(1)

(2)

(3)

(4)

最后将式(2)～(3)求得的数据代入式(1)来求得极大似然估计值,进而得到相对应的项目参数估计值.

1.3 MCMC算法

MCMC是马尔可夫链与蒙特卡罗方法的结合,即构造合适的马尔可夫链进行抽样并使用蒙特卡罗方法进行积分计算,进而使马尔可夫链最后达到收敛平稳的状态,Metropolis方法与W.K. Hastings的概括奠定了MCMC方法的基石[13-14].此方法在以π(x)为平稳分布的马氏链上产生相互依赖的样本,即MCMC方法在本质上是一个蒙特卡罗综合程序,它的随机样本的产生与一条马氏链有关.基于条件分布的迭代取样是另一种重要的MCMC方法,其中最著名的特殊情况就是Gibbs抽样,它现已成为统计计算的标准工具,其最吸引人的特征是其潜在的马氏链是通过分解一系列条件分布建立起来的.W.K. Hastings[14]推广了Metropolis采样法,在吉布抽样中采用Metropolis采样法对条件分布进行抽样,可以避免计算条件分布的正规化常数现象,被称为MH within Gibbs[15].

本文在这3个模型下的MCMC估计均采取吉布斯的MH采样法,通过Gibbs采样法对未知参数的联合后验分布进行分解,然后应用MH采样法对各个参数的全条件分布进行取样,以构建未知参数后验分布为平稳分布的可逆的马尔可夫链,从而进行取样,这样就可以将取样所得到的样本分布近似为目标分布,通过对近似分布推断来实现参数估计.在DINA模型、DINO模型以及G-DINA模型上分别采用MCMC算法进行项目参数估计,具体步骤如下:

(i)确立未知参数的联合后验分布为目标分布(平稳分布).在局部独立性假设满足情况下,DINA模型的联合似然函数为

DINO模型的联合似然函数为

GDINA模型的联合似然函数为

在贝叶斯框架中,给定得分矩阵的条件,所有参数的联合后验分布(即平稳分布)为

P(α,s,g|X)∝p(X|α,s,g)P(α,s,g)∝p(X|α,s,g)p(α)p(s)p(g),

P(α,δ|X)∝p(X|α,δ)P(α,δ)∝p(X|α,δ)p(α)p(δ).

在给定得分矩阵和其余参数条件下,各个参数的全条件分布为

p(α|X,s,g)∝L(α,s,g)p(α),p(g|X,α,s)∝L(α,s,g)p(g),p(s|X,α,g)∝L(α,s,g)p(s),p(δ|X,α)∝L(α,δ)p(δ),p(α|X,δ)∝L(α,δ)p(α),

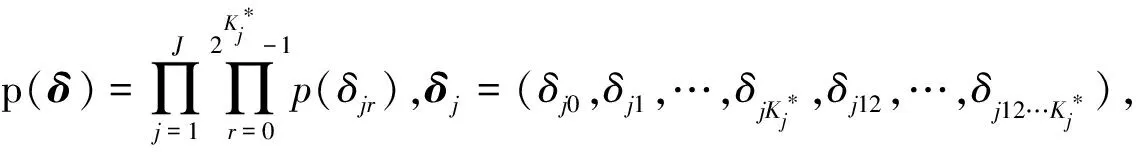
αik～Bernoulli(0.5),s～Beta(1,1),g～Beta(1,1)∈

(ii)设定各参数初值,即按各参数的先验分布生成参数初值.

(5)

(6)

将式(5)和式(6)计算出的转移概率与随机数r～U(0,1)进行比较,若转移概率大于等于r则接受转移,否则不转移.

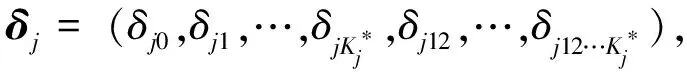
1.4 知识状态估计

在EM算法估计出项目参数后,可采用属性的边际后验概率(MPPE/EAP)估计被试知识状态(即被试i掌握属性K的边际概率),其计算公式为

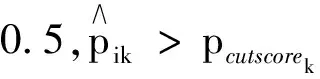
知识状态在MCMC算法中为未知的随机向量,可直接从近似平稳分布中所取的样本计算均值,然后通过上述同样的划界分数方法可得到被试在各属性上的知识状态估计,进而得到估计的知识状态.

2 模拟研究

2.1 研究目的

在不同条件组合下,探讨DINA模型、DINO模型和G-DINA模型下的EM算法和MCMC算法估计参数的表现.

2.2 研究设计

考虑到4个主要的影响因素:3种类型认知诊断模型(3个水平)、样本量(在DINA模型和DINO模型上为2个水平,在GDINA模型上为3个水平)、题目参数(2个水平)、测验长度(2个水平).所采用的Q矩阵如图1所示,其中20题和30题分别对应Q1、Q2,参照J. de la Torre等[4]的设定:在30道题目上考察5个相互独立属性,1～10道题考察了1个属性,11～20题考察了2个属性,21～30题与1～10题一样只考察了1个属性.样本量在DINA模型和DINO模型上分别设定为500、1 000.考虑到G-DINA模型的复杂性,在该模型上的3个水平样本量分别设定为500、1 000以及2 000.题目质量分别设定了高质量、低质量2个水平的项目参数,参照文献[16]在DINA模型上猜测参数与失误参数分别服从U(0.05,0.25)和U(0.05,0.40)的设定,并在此基础上进行细化,其中在DINA模型、DINO模型下高质量题目参数满足失误参数s和猜测参数g都服从均匀分布U～(0.05,0.15),低质量题目参数满足失误参数s和猜测参数g都服从均匀分布U～(0.25,0.35).而在G-DINA模型上,未掌握的概率与答对题目概率参数在高质量水平下分别服从均匀分布U～(0.05,0.15)和U～(0.85,0.95),在低质量水平下分别服从均匀分布U～(0.25,0.35)和U～(0.65,0.75).程序通过R语言编写,其中EM算法使用Ma Wenchao等[17]所开发的GDINA包,MCMC算法使用JAGS来实现[9].

2.3 评价指标

(i)采用偏差(fBIAS)、均方根误差(fRMSE)和绝对偏差(fABS)指标来考察参数估计的精度,这3指标值越接近0说明估计精度越高,由估计精度的高低来评价参数估计的返真性.

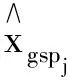
(ii)运用模拟的平均属性判准率(attribute accuracy rate)来评价知识状态判准率,其值越高模型的表现越好,其计算公式为

2.4 实验结果

表1～表4分别是EM算法与MCMC算法在DINA模型、DINO模型和G-DINA模型上的参数估计的偏差、均方根误差以及绝对偏差.

从表1可以看出:在DINA模型上,无论哪种条件,EM算法的失误参数都会对出现低估现象,而在DINO模型上却相反,这可能跟模型本身类型有关;同时在题目质量低的情况下,在DINA模型和DINO模型上,EM算法对猜测参数也会出现低估现象.从整体来看,在题目质量较低、样本量N=500以及测验长度L=20的组合条件下,MCMC算法在DINA模型和DINO模型上的表现更优于EM算法的表现.从表4可以看出:在G-DINA模型上,无论是高质量题目还是低质量题目,在样本量N=1 000与测验长度L=20的条件组合下,MCMC算法均优于EM算法.但随着样本量的增大和测验长度变长,EM算法估计出的项目参数越来接近真值.

从表2～表4可以看出:无论哪个模型的哪种条件,MCMC算法下参数估计的均方根误差均优于EM算法下参数估计的均方根误差,尤其是在题目质量较低和小样本量的组合下,有着非常明显的效果,均方根误差差值均超过0.020;在DINA模型和DINO模型上的参数估计偏差的差值为0.015左右,在G-DINA模型上超过0.020.这表明了MCMC算法对参数估计的精确度高,且更适用于题目质量较低和小样本量的组合条件.但随着样本量的增大,EM算法在3个模型上的表现在大多数情况下却是都略优于MCMC算法在3个模型上的表现.

表1 2种算法在DINA模型和DINO模型上的参数估计偏差

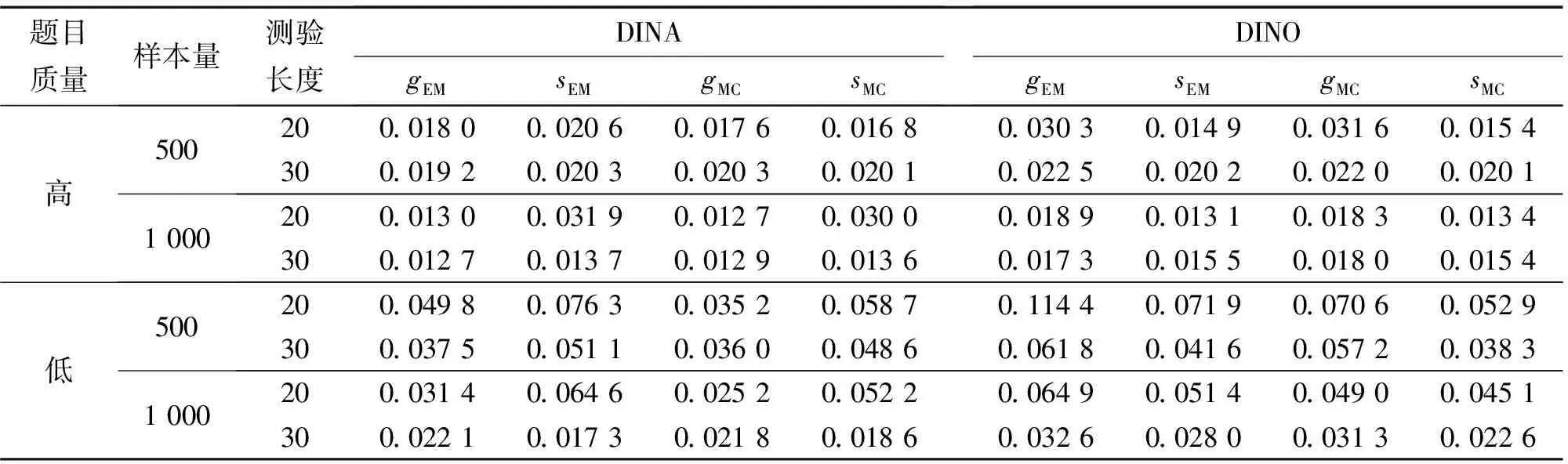
表2 2种算法在DINA模型和DINO模型上的参数估计均方根误差

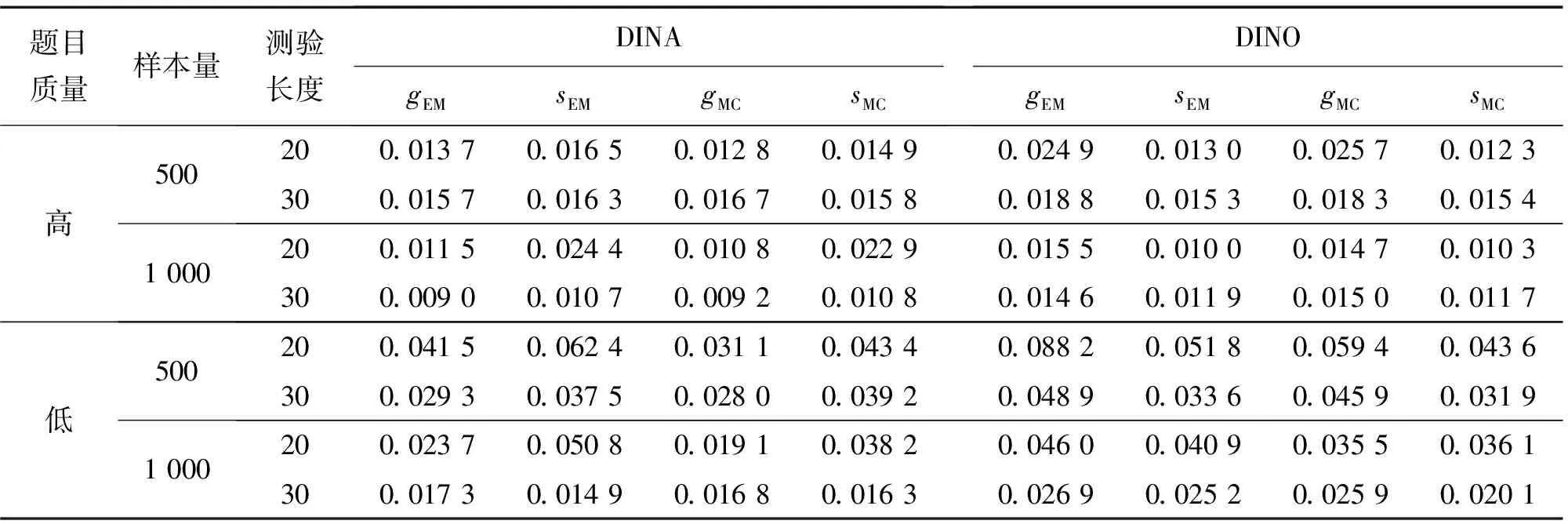
表3 2种算法在DINA模型和DINO模型上的参数估计平均绝对离差

表4 2种算法在G-DINA模型上的参数估计偏差、均方根误差以及估计平均绝对离差

表5和表6分别是EM算法与MCMC算法在DINA模型、DINO模型和GDINA模型上得到的平均属性判准率,由表5和表6可以看出:随着题目质量的提高、样本量的增大以及测验长度的增长,这2种算法的平均属性判准率增大,且越来越趋于一致.但在题目质量较低时,MCMC算法下得到的平均属性判准率明显优于EM算法下的平均属性判准率,特别是在GDINA模型上,当测验长度L=20与样本量N=500或者N=1 000的条件组合时,在这2种算法下得到的平均属性判准率差值为0.04左右,这说明了MCMC算法在题目质量较低与短测验长度组合条件下的优越性.

表5 2种算法在DINA模型和DINO模型上的平均属性判准率

表6 2种算法在GDINA模型上的平均属性判准率

3 结论和讨论

本文通过引入EM算法和MCMC算法,基于认知诊断3种模型,在多种条件组合下进行项目参数估计,通过比较偏差、均方根误差、绝对偏差、平均属性判准率来详细分析在不同条件组合下这2种算法在这3种模型上进行参数估计的效果.

当题目质量较低、测验短以及小样本这3种条件的组合时,MCMC算法得到的偏差、均方根误差、绝对偏差、平均属性判准率的值均优于EM算法下得到的值.但若项目质量变高或者测验变长、样本量变大,则EM算法下得到的数据就略优于MCMC算法下得到的值,同时在该条件下,考虑到MCMC算法在R程序中的运行时间过长,不如EM算法计算快捷,故在题目质量较高或者测验长、样本量大的条件下推荐使用EM算法进行参数估计,在题目质量较低、测验短以及小样本的条件下使用MCMC算法进行参数估计.

本文只考虑了在认知诊断中常用的3个模型,在其他模型上不同条件下,EM算法和MCMC算法进行参数估计的效果如何,值得思考.如本文所采用的Q矩阵仅考察了2个属性,而在实际应用中可能不限于2个属性,在3个属性甚至多个属性下EM算法和MCMC算法进行参数估计的效果如何;有些研究在属性层级模型下考虑了EM算法的表现[18],在不同知识状态分布和Q矩阵设计[19]条件下,这2种算法表现如何.Liu Yanlou等[20]将这2种算法用于在DINA模型下的误差估计.纵向认知诊断模型的参数估计算法大多数采用MCMC算法[9],也有些研究针对纵向GDINA模型提出了EM算法[21],故在纵向认知诊断模型下这2种算法的表现也有待进行比较研究.另外,在估计未知参数标准误方面[22],MCMC算法表现如何,有待考虑.