一种基于Logistic回归的基本信度分配函数的构造新方法

刘邱云,王璐璐,黄 涛

(1.江西师范大学数学与统计学院,江西 南昌 330022;2.江西经济管理干部学院财务与金融学院,江西 南昌 330088)

0 引言

Logistic回归[1-3]模型分类方法是在统计分析领域中基于具体模型的分类方法，它在处理分类问题时，既能对样本所属的类别进行预测，又能对分类的相关概率信息进行计算.此方法常被用于疾病诊断、经济预测及数据挖掘等领域[4-5].

证据理论[6]作为不确定性推理的一种重要方法,能较好地表达及融合决策层的不确定信息,较广泛地应用在决策分析、信息融合以及模式识别等领域[7-9]中.使用证据理论做不确定性推理,首先要解决如何表示不确定性信息,即构造基本信度分配(BBA)函数问题.

在运用证据理论时，基本信度分配函数作为一种集值随机变量即随机集[10],它的构造方式与具体运用紧密相关.李世诚等[11]利用马尔可夫随机场(MRF)构造BBA函数，建立了图像邻域证据场.童涛等[12]借助SVM分类结果作为独立证据生成BBA函数,解决了对SAR图像目标的有效分类.李新德等[13]结合PNN网络生成目标识别矩阵以获取BBA函数,提出了一种面向多特征飞机图像目标的信息融合方法.S. Petit-Renaud等[14]基于非参数回归分析针对已知的输入向量，预测输出变量的值，得到模糊信任分配(FBA)函数,并构造为集值模糊集上的一个BBA函数.XU Peida等[15]用一种非参数方法生成BBA函数,以处理测试样本与概率间的关系模型中的分类问题.M.C. Garrido等[16]针对不完全信息和异构的分类问题，基于回归方法构造了不完整数据集上的证据函数.就以上研究趋势可以发现:基本信度分配函数的构造侧重利用问题内在的不确定性[17],尤其是对无法用概率描述的不确定性建立模型,以体现证据理论在处理不确定性问题中的优势.与以上研究相比较，Logistic回归是一种更简单的模型，尤其对于大规模的线性分类，操作更方便.Logistic回归利用非线性映射,将离分类平面比较远的点的权重大大降低,而与分类更相关的数据点的权重就得到了相对提高.基于此,本文结合Logistic回归分类,提出一种新的证据理论基本信度分配函数的构造方法.

本文的主要贡献有如下2方面:(i)首先以多类Logistic回归分类法输出的样本后验概率和分类正确率建立证据权重系数，其次再建立加权的基本信度分配函数，最后通过加权D-S证据融合进行决策，判别样本所属的类别；(ii)将构造的新方法应用于多特征图像分类.

1 Logistic回归分类

1.1 2类Logistic回归分类法

假设n个训练样本是{x,y},其中x=(x1,x2,…,xn),xi是d维的样本特征向量,y={y1,y2,…,yn},此处用1和0作为类别标签，分别表示正类和负类，则将样本x归入类别中正类的“概率”为

p(y=1|x;θ)=g(θTx)=1/(1+e-θTx),

这里θ是d维的模型参数,也就是回归系数,g(θTx)是Logistic函数.

本文使用极大似然估计方法来求解模型参数，由于直接对似然函数进行最大化通常较麻烦，因此先将似然函数取对数，再最大化.这里,

进一步,转换成代价函数：

事实上,对代价函数最小化就相当于对似然估计最大化，再结合梯度下降法对l(θ)的极大值进行求解，最终得到参数θ.

1.2 多类Logistic回归分类法

为了将2类回归分类法推广为多类回归分类法，这里使用one-vs-all策略，即假设分类问题中有c个类，将其中某一个类作为一类，而其余的类作为另一类，以此建立一个2类分类器，按这种方式一共可以建立c个2类分类器.假设类别标签y∈{1,2,…,c},c个参数θi(i=1,2,…,c),则

(1)

2 权重BBA函数的构造及分类

2.1 权重BBA函数的构造

定义2设同一识别框架Θ上有2个独立证据，其基本信度分配函数分别为m1和m2,则用D-S组合规则融合后的证据m=m1⊕m2为

(2)

定义3假设有Q个样本，其中所属类分类正确的样本个数为q,则样本分类正确率为

E=q/Q.

(3)

定义4假设分类器包含c个类,其识别框架为Θ={L1,L2,…,Lc},E(Li)为分类器对第i类的分类正确率,则第i类的权重系数分配函数为

(4)

其中n=|Θ|,这里正整数k越大表明分类正确率越高,即赋予的权重越大.由此可见权重系数W(Li)体现了各证据的可靠程度.

定理1假设分类训练样本集的样本共有n个特征，使用Logistic回归分类法对第j个特征进行训练，由式(3)得分类正确率为Ej(Li),由式(4)得权重系数为Wj(Li)(j=1,2,…,n;i=1,2,…,c),xs为待识别样本,利用式(1)代入第j个特征可求得pj(y=i|xs),引入折扣因子α(α≥1)有

于是建立第j个特征对应的权重BBA函数mWj为

(5)

2.2 分类步骤

步骤如下:

(i)提取样本的若干个特征(假设有n个);

(ii)利用训练样本集中类别已知的样本,求解回归参数θi(i=1,2,…,c);

(iii)通过式(5)建立加权的基本信度分配函数mW(Li);

(iv)利用式(2)对这些基本信度分配函数做D-S证据融合mW1⊕mW2⊕…⊕mWn(Li),最后根据argmaxmW1⊕mW2⊕…⊕mWn(Li)=Li0做决策,即将待分类样本xs归入第i0类.

3 应用于图像分类

为了将上述新方法应用于图像分类，本文选取在Scene 15场景分类数据集中的kitchen(K)、livingroom(L)及bedroom(B) 3类室内场景图像作为分类对象.每个类型含200幅图像，随机选取100幅图像作为训练样本，另外100幅图像作为验证样本.对比模型为Hu不变矩、单一纹理特征和加权D-S证据融合特征.

由于在图像分类中，图像的Hu不变矩与纹理特征相互独立，所以使用加权D-S证据融合的做法是合理的.

模型应用于图像分类的流程图如图1所示，其步骤如下:

(i)提取场景图像样本的特征量——Hu不变矩和纹理特征;

(ii)根据2个特征量,对类别已知的100幅图像进行训练,求解出Logistic回归参数θi(i=1,2,3),并依次计算出2个特征量的正确率和权重系数,然后借助式(1)将验证样本中提取的特征代入,得到p(y=Li|x),其中Li∈(K,L,B);

(iii)通过式(5)构造加权的基本信度分配函数mW(Li),其中Li∈(K,L,B);

(iv)最后通过式(2)做D-S证据融合,并根据argmaxmW1⊕mW2(Li)判定验证样本的类别.

图1 图像分类流程图

3.1 提取图像特征

对于图像分类，本文提取在图像矩特征量中的Hu不变矩及在纹理特征中的灰度共生矩阵.

3.1.1 Hu不变矩 图像的矩特征是以图像分布的各阶矩来描述灰度的统计特征的方法，它具有较好的平移、旋转和比例不变性.借助2阶和3阶中心矩,M.K. Hu构造了如下表达式的7个不变矩:

f1=η20+η02,

f3=(η30-3η12)2+(3η21-η03)2,

f4=(η30+η12)2+(η21+η03)2,

f5=(η30-3η12)(η30-η12)((η30+η12)2-3(η30+η12)2)+(3η21-η03)(η21+η03)(3(η30+η12)2-(η03+η21)2),

f6=(η20-η02)((η30+η12)2-(η03+η21)2)+η11(η30+η12)(η03+η21),

f7=(3η21-η03)(η30+η12)((η30+η12)2-3(η03+η21)2)+(3η12-η30)(η21+η03)(3(η30+η12)2-(η03+η21)2),

其中ηpq(p,q=0,1,2,3)表示归一化中心矩.用100个训练样本和100个验证样本的7个Hu不变矩特征构造出图像的矩特征向量为

FA=(f1,f2,f3,f4,f5,f6,f7).

3.1.2 纹理特征 图像的纹理特征通过灰度共生矩阵的4个指标(熵T1、能量T2、对比度T3、相关性T4)来描述.其中熵T1描述了纹理的复杂程度和非均匀程度,能量T2描述了图像的纹理粗细度和灰度分布的均匀程度,对比度T3描述了某像素值的亮度与其领域像素值的亮度的对比情况,相关性T4描述了纹理的一致性.它们的表达式分别为

其中Pi, j即为P((i,j)/d,θ).这里θ表示方向;d表示距离;P为灰度共生矩阵;μi表示灰度共生矩阵各行的均值,μj表示各列的均值;σi表示灰度共生矩阵各行的标准差,σj表示各列的标准差.构造出图像的纹理特征向量为FB=(T1,T2,T3,T4).

3.2 实验与结果分析

首先从提取到的3类室内场景图像样本的Hu不变矩和纹理特征中随机选出100个训练样本，利用多类Logistic回归分类法进行参数学习，以获得优化参数θi(i=1,2,3);再把训练样本代入训练好的模型中以获取上述3类样本的分类正确率Ej(Li),结果如表1所示.

表1 各特征的分类正确率

然后以上述特征为证据体(k=2),按照定义4处理得到2个特征的加权系数,结果如表2所示.

表2 各特征的加权系数

最后对100个验证样本进行测试，针对不同的折扣因子α值,分别得到样本单一特征的平均分类正确率与加权融合的平均分类正确率，结果如图2所示.

图2 α取不同值的各特征的分类正确率

由图2可知:通过加权D-S证据融合后的平均分类正确率高于单一特征的平均分类正确率；根据单一的纹理特征或Hu不变矩特征分类的正确率不稳定，尤其是单一的纹理特征起伏更加明显，而加权D-S证据融合特征分类的正确率高且相当稳定，因此可信度较高.

当折扣因子α=3.5时，各特征的分类正确率和F均值结果如表3所示.其中图像bedroom(B)样本采用2种单一特征分类的正确率分别为0.64、0.72,采用加权D-S证据融合特征后正确率提高到0.86;图像livingroom(L)样本的分类结果类似，采用2种单一特征分类的正确率分别为0.79、0.78，采用加权D-S证据融合特征后正确率提高到0.84；而图像kitchen(K)样本的Hu不变矩的分类正确率低于加权D-S证据融合特征后的分类正确率,K样本的纹理特征的分类正确率高于加权D-S证据融合特征后的分类正确率,恰好与D-S证据理论的特点相符,即降低证据之间的冲突程度，增大可信度.根据F均值分析数据可得类似结果.

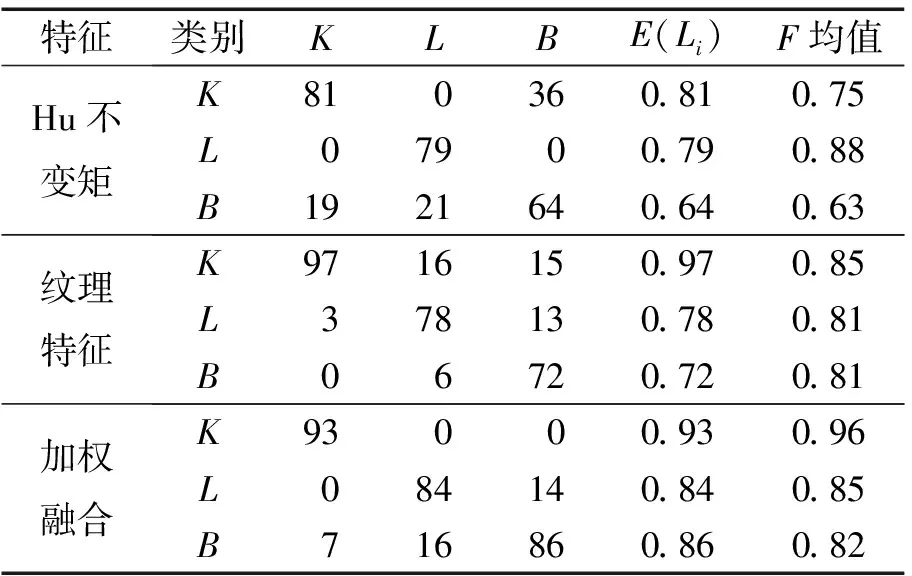
表3 各特征的正确率混合矩阵

4 结论

本文提出了一种新的基于Logistic回归分类模型的基本信度分配函数的构造方法，并且在多特征图像分类上验证了该方法的有效性.这种新方法利用多类Logistic回归分类法，分别基于单一纹理特征和Hu不变矩对图像样本进行初步识别，并以Logistic回归分类法输出的后验概率与分类正确率建立证据权重系数，从而构造出加权的基本信度分配函数；最后利用加权D-S证据理论对样本的各个特征信息进行有效融合，并根据融合后的最大值对样本所属的类别做决策.实验结果显示:本文提出的新方法实现了多特征的有效融合，既提高了分类的正确率，又改正了使用单特征导致的分类正确率的不稳定的缺点.