基于吸收度的三支决策社团划分算法
万仁霞,张宇红,苗夺谦
(1.北方民族大学数学与信息科学学院,宁夏 银川 750021;2.同济大学计算机科学与技术系,上海 201804)
0 引言
在现实世界中存在着各种各样的网络,如城市交通网络[1]、社会网络[2]、生物网络[3]等,它们都可以抽象成复杂网络.而复杂网络又是由若干个社团构成的,社团的结构性[4]主要表现为:在同一个社团中的节点联系较为紧密,在不同社团间的节点联系较为稀疏.研究网络的社团结构可以更加准确地理解复杂网络的拓扑结构及其内在原理.因此,如何有效地进行社团划分是社团研究者们的研究方向之一.
近年来,许多学者从不同角度对网络的社团划分[5]算法进行了研究.Newman快速算法(Newman fast algorithm,NFA)[6]依靠模块度获得最佳社团结构;自包含GN算法[7](self-contained GN algorithm)给出了强社团结构和弱社团结构2种变量的定义,为社团结构的好坏提供了一种参考标准;B.W. Kernighan等[8]提出了基于图划分的社团划分算法,该算法需要提前预知社团划分的数目才可以实现社团划分;U.N. Raghavan等[9]提出一种快速标号传播算法(label propagation algorithm,LPA),该算法利用网络自身结构来判定社团结构,复杂度较低且收敛快,但缺点是比真实社团结构的精度略低.上述算法从不同角度和不同层面对复杂网络的社团划分问题进行研究,并取得了一定的研究成果.目前,社团划分算法大多数是非重叠的社团划分算法,其对于重叠部分的处理采用传统的二支决策技术,即根据已有的信息、社团对节点的归属做出接受或拒绝的判决.然而,由于信息的模糊或不充分等因素,许多网络存在重叠的社团结构[10],所以基于二支决策技术的社团划分会导致社团划分结果的不可靠问题.因此,如何对网络中重叠部分的节点进行有效地划分,以便发现社团潜在的规律,已引起了许多学者的关注.李敏毓等[11]提出一种社团结构特征研究,旨在处理在社交网络中的重叠社团并解决现有的社团划分算法结果分辨率低的问题.LFM(largest fitness measure)是基于局部优化的适应度函数的社团发现算法[12],该算法在发现网络中的重叠社团和有关层次结构的社团方面具有较好的效果.郭娜等[13]提出了一种基于最大生成树的重叠社团发现算法,该算法对初始社团划分结果进行优化,且避免了社团之间重叠的出现.
三支决策(three-way decisions,3WD)理论[14]的思想是由决策粗糙集理论(decision-theoretic rough sets,DTRS)[15]产生的,旨在解决在现实世界中的不确定信息的决策问题,为模糊信息处理[16]提供一种新的解决思路.由于三支决策符合人类思维和认知特点,能较好地处理在实际决策过程中出现的不确定性问题,所以它一经提出便得到国内外学者的广泛关注.杨雪洁等[17]提出了一种基于子模优化的边界域处理社团发现算法,旨在用三支决策模型及子模优化思想来划分社团结构.方莲娣等[18]提出一种基于三支决策的非重叠社团划分算法,该方法将初始聚类形成的重叠社团进行2次划分以形成最终的非重叠社团.
本文通过节点的重要度来刻画节点间的关系,采用三支决策思想来解决社团节点重叠问题,提出了一种基于吸收度的三支决策社团划分算法,即根据不同节点归入不同社团域的动作参数所产生的损失函数来定义吸收度,并依据吸收度对已获取的重叠节点进行划分,不仅较好地体现了节点的真实归属,还可以获取更好地接近全局最优社团.本文采用3个真实的网络数据集对3WD-PPOC算法进行了验证,实验结果表明本文所提算法对在社团中的节点处理可行且有效.
1 相关概念
1.1 节点属性重要度
在一个无向无权网络G=〈V,E〉中,节点集合为V,边集合为E,在节点集合V中一对点即对应边集合E中的一条边.
定义1[19]设节点集合V={e1,e2,…,en},令(ei,ej)表示节点ei与节点ej之间的边,若ei和ej相连,则边存在;若ei和ej不相连,则边不存在.边集E={(ei,ej):ei,ej∈V;1≤i,j≤n},则节点ei的度Di表示ei的邻居节点的数目,即与该节点连接的其他节点的数目,Di的表达式为
Di=|{(ei,ej):ei,ej∈V;(ei,ej)∈E}|.
定义2[20]设节点集为V={e1,e2,…,en},那么在节点集中所有节点的平均度为〈k〉,〈k〉的表达式为
由于ei、ej属于同一网络,且Di表示节点ei的邻居节点数目,于是可得到如下节点平均度的结论.
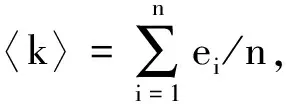
定义3[21]邻接矩阵Wn×n表示在网络中节点ei与节点ej之间的连接关系,其中wij为在邻接矩阵中对应的元素,取值为0或1,n为节点总数,即若节点ei和ej之间有连接关系,则wij=1;若节点ei和ej之间没有连接关系,则wij=0.
定义4[22]节点重要度矩阵H的定义为
其中将矩阵对角线上的元素全部置为1,它表示在网络中每个节点对于自身的重要度贡献比值为1.由定理1知,在网络中的节点重要度矩阵H是网络邻接矩阵的映射.当i≠j时,wij映射为wijDj/〈k〉2;当i=j时,wij映射为1.
1.2 三支决策
三支决策[23]理论对于在信息处理中不确定决策问题的解决具有高效性,尤其是对信息不精确、条件不充分的情况.其核心思想是将决策项分成3 种决策规则,分别是正域决策、负域决策和边界域决策.当证据不完整、不充足时,可以采用边界域决策;当证据精准、完善时,可以采用正域决策或者负域决策.正域决策和负域决策是明确的,即三支决策主要围绕边界域的处理展开研究.
三支决策的研究主要基于决策粗糙集,整个论域被划分为3个部分,即正域(POS)、负域(NEG)和边界域(BND),分别代表接受、拒绝和不承诺3种决策结果.决策粗糙集模型理论[24]将概率粗糙集和最小风险贝叶斯决策结合起来,通过计算各类决策风险损失值,对正域(POS)、负域(NEG)和边界域(BND)进行划分.
文献[24]对三支决策给出了具体解释:假设有3种状态的集合Ω={X1,X2,X3},对应于概率粗糙集上的正域、负域、边界域.由分类结果的3个域构造出一个决策动作集D={αP,αN,αB},其中αP、αN、αB分别代表将一个对象分类到概率粗糙集上的正域、负域、边界域的决策动作,且不同的决策动作代表不同的分类结果.
2 基于吸收度的三支决策社团划分算法
三支决策模型根据对象的正域、负域、边界域采取不同的决策规则,尤其在处理不确定性问题时,可以通过信息量的增多,做出更为准确的判决.
2.1 社团中的3个域
基于三支决策的思想,实现对网络重叠社团结构的划分.对于初始社团划分后获得的重叠社团结构的定义如下:
(i)正域(POS)表示被考察社团的非重叠节点;
(ii)边界域(BNG)表示重叠部分的节点;
(iii)负域(NEG)表示除正域及边界域外的节点.
如图1所示,左右2个椭圆分别代表2个社团结构,且这2个社团之间存在社团重叠结构,即节点5、节点6以及节点7.网络节点集为V={1,2,3,4,5,6,7,8,9,10,11},社团X={1,2,3,4,5,6,7},依据三支决策思想,正域QPOS(X)={1,2,3,4},边界域QBND(X)={5,6,7},负域QNEG(X)={8,9,10,11}.

图1 重叠社团3个域的划分
显然,社团结构满足如下性质.
性质1在网络G=〈V,E〉中,对于任意社团X,有:(i)QPOS(X)∪QBND(X)∪QNEG(X)=V;(ii)QPOS(X)、QBND(X)、QNEG(X)两两相交为空.
这表明:社团的正域、边界域、负域是网络节点的一个划分,且当在社团中的2个域明确后,其余1个域也是确定的.因此,在本文中,仅讨论社团的正域、边界域的构成,不对负域赘叙.
2.2 吸收度
借鉴三支决策阈值[25]的概念,本文给出社团划分的吸收度定义.
定义5假设一个社团可以划分为Ω={Y1,Y2,Y3},即对应于社团的正域、负域、边界域.当在社团中的节点归到不同的社团域中时,可以得到不同的动作参数L={αP,αN,αB},其中αP、αN、αB分别代表节点归入不同社团域的动作参数,且不同的动作参数代表不同的社团域划分结果,可能出现9种损失函数(见表1).其中第1列函数表示当节点归入社团Y1,动作参数为αP、αN、αB时带来的损失函数,记为λPY1、λNY1、λBY1;第2列函数表示当节点归入社团Y2,动作参数为αP、αN、αB时带来的损失函数,记为λPY2、λNY2、λBY2;第3列函数表示当节点归入社团Y3,动作参数为αP、αN、αB时带来的损失函数,记为λPY3、λNY3、λBY3.

表1 损失函数
节点归入不同社团域可以得到不同的损失函数,因此不同节点在不同的情况下会归入不同的域.本文将根据吸收度的不同职能,将吸收度区分为F吸收度和P吸收度:
F=(λPY3-λBY3)/((λPY3-λBY3)+(λBY1-λPY1)),
(1)
P=(λBY3-λNY3)/((λBY3-λNY3)+(λNY1-λBY1)),
(2)
其中F吸收度用来控制社团边界域的形成,P吸收度用来控制社团边界域节点的再划分.
可以证明,F、P吸收度满足如下性质.
性质20≤P 本文首先根据重要度矩阵,给出非重叠的社团划分算法,该算法在不引入吸收度时形成了初始社团结构.主要实现步骤如算法1所示. 算法1PPC算法. 输入:无向无权网络G=〈V,E〉及重要度矩阵H. 输出:网络社团Aj(j=1,2,…,k). (i)计算网络的节点重要度矩阵H; (ii)随机选择k个节点z1,z2,…,zk,作为初始社团的中心,令Aj={zj}(j=1,2,…,k); (iv)计算各社团中心,若各中心未发生变化,则转入步骤(v),否则,转向步骤(iii); (v)输出社团Aj(j=1,2,…,k). 在步骤(iii)中的HZ代表在社团中所有需要被考察节点Z的重要度值. 算法1实际上是一种典型的非重叠社团划分的算法,为重叠社团划分创造了初始社团结构.不同于一般社团构建的算法,本文的算法采用节点重要度来划分节点的社团归属. 本文结合三支决策思想,引入吸收度的概念,在上述算法产生的初始社团结构的基础上进行局部再划分处理,从而达到对重叠社团节点的更精细划分,其主要实现步骤如下. 算法23WD-PPOC算法. 输入:无向无权网络G=〈V,E〉、重要度矩阵H及λPY1、λNY1、λBY1、λPY2、λNY2、λBY2、λPY3、λNY3、λBY3值. 输出:无重叠网络社团结构. (i)计算网络的节点重要度矩阵H; 考虑到人们在工厂工作而Milk-run在生产供应路线上行驶的事实,必须解决某些安全问题。首先,火车必须可以自由进出Milk-run运输车道,并且路线上不应放置任何物料,因为这些因素可能对司机构成威胁并导致延误。为了使员工关注工厂内的交通情况,必须对车道进行清晰的标识,并且培训员工如何应对车辆的流通,Milk-run火车必须拥有绝对的优先通行权。 (ii)随机选择k个节点z1,z2,…,zk,作为初始社团的中心,令Aj={zj}(j=1,2,…,k); (iv)计算各社团中心,若各中心未发生变化,则转入步骤(v),否则,转向步骤(iii); (v)通过式(1)~(2)计算F吸收度和P吸收度; (vi)对于任意网络节点Z,若存在社团Al、Am,有||HZ-Hzi|-|HZ-Hzk||≤F,则将节点Z归入社团Al、Am的边界QBND(Al)、QBND(Am),即Z为社团Al、Am的共同边界点(社团重叠节点); (vii)构建社团正域:QPOS(Ai)=Ai-QBND(Ai) (i=1,2,…,k); (x)更新QPOS(Aj0)的中心rj0; (xi)更新边界域:QBND(Aj)=QBND(Aj)-{Z} (j=i1,i2,…,il); (xii)若QBND(Al)≠∅(l=1,2,…,k),则转步骤(ix),否则,转步骤(xiii); (xiii)输出社团正域QPOS(Ai)(i=1,2,…,k). 算法2的步骤(i)~(iii)实际上执行的是算法1的内容,对重叠社团的划分起到初始化的作用.即算法2是算法1引入吸收度概念后的改进,从而能更好地处理重叠社团节点的划分.其中,在步骤(vi)中的F吸收度用于形成社团边界域,可以刻画社团的重叠区.步骤(ix)是对社团重叠区的节点(即边界域中的节点)进行最终的社团归属判决,P吸收度用于刻画边界域中节点的划分.F吸收度作用于边界粗社团的形成过程,即若F吸收度值越大,则所构成的社团结构就越粗糙;P吸收度作用于区分边界域中社团节点的细化过程,即若P吸收度越小,则边界社团中节点的划分就越精细.由于算法的边界域是基于多个社团的共同边界点而产生的(即步骤(vi)),不同于一般的三支决策处理类似问题(如三支聚类[26])的结果,所以在本文算法的边界域中的节点同时为多个社团潜在的节点,这为步骤(ix)~(xii)在多社团边界域上开展更新提供了必要条件. 算法输出为社团正域,可以证明这些社团正域满足如下的性质. 性质3在无向无权网络G=〈V,E〉中,经过算法2产生的社团正域QPOS(Ai)(i=1,2,…,k)满足: (ii)QPOS(Ai)∩QPOS(Aj)=∅(1≤i,j≤k,且i≠j). 即经过算法2后输出的所有社团正域是整个网络节点的一个有效划分. 为了验证本文所提算法的有效性和可行性,本文采用了3个典型的社交网络数据集作为实验数据集,分别是著名的空手道俱乐部成员网络(Zachary′s karate club)、足球联盟网络(American college football)和海豚社会关系网络(Dolphins).数据集可在网上(http://www-personal.Umich.edu/~mejn/netdata)的数据集中获取.数据集的基本信息如表2所示. 实验环境为英特尔酷睿双核P8500处理器,内存8 GB,64位Windows10操作系统.主要编程语言为Matlab、R语言编程工具. 表2 实验数据集 衡量社交网络中社团划分质量的标准主要有内部评价指标和外部评价指标[27-29]. 3.2.1 内部评价指标 在社交网络中,模块度函数作为社团划分好坏的量化标准已经被广泛使用. 模块度函数Q[28]定义如下: 若社团内部边的比例不大于在任意连接时的期望值,则有Q=0,且Q的上限为1.若社团结构越明显,则越接近1.在实际的网络中,Q的取值范围一般为0.3~0.7. 3.2.2 外部评价指标NMI指标[29]可以用来估计具有已知分区的真实社团结构与社团划分结果之间的相似性.NMI反映了划分的社团结构与真实社团结构非常相似,若NMI值为1,则2个社团结构完全相同,若NMI值为0,则2个社团结构完全不同.其计算公式为 NMI(X|Y)=1-(H(X|Y)+H(Y|X))/2, 其中X表示原社团结构的集合;Y表示使用本算法得到的社团结构的集合;H(X|Y)表示X在Y上的规范化条件熵;H(Y|X)表示Y在X上的规范化条件熵. 3.3.1 吸收度与模块度的关系 从3WD-PPOC的算法描述可以看出,损失函数通过吸收度F、P来影响社团划分的效果,图2直观展示了本文算法(3WD-PPOC)的吸收度F、P对模块度Q的影响.从图2可以看出,对于Zachary数据集,当损失函数为λPY1=0、λPY3=6.4、λNY1=13.6、λNY3=0、λBY1=4、λBY3=0.4时,F、P吸收度为(F,P)=(0.60,0.40),此时模块度参数最优值为0.417;对于Football数据集,当损失函数为λPY1=0、λPY3=5.6、λNY1=15.6、λNY3=0、λBY1=4.5、λBY3=0.1时,F、P吸收度为(F,P)=(0.550,0.005),模块度参数最大值为0.604;对于Dolphins数据集,当损失函数为λPY1=0、λPY3=5.6、λNY1=15.6、λNY3=0、λBY1=4.5、λBY3=0.1时,F、P吸收度为(F,P)=(0.550,0.005),此时模块度参数最佳值为0.546. 图2 基于实验数据集吸收度与模块度的关系图 3.3.2 基于典型数据集的划分效果 (i)基于Zachary 空手道俱乐部网络实验.Zachary空手道俱乐部网络[30]是美国某大学空手道俱乐部的关系网络,该网络包含34个节点及78条边,其中节点表示俱乐部成员,边表示成员之间存在的关系.Zachary空手道俱乐部成员关系网络是复杂网络、社团发现技术等领域的典型测试网络数据集,在网络中的人物关系因某种原因而被分成若干个小社团,该网络的原始结构如图3所示. 图3 Zachary网络初始社团结构 据上述“吸收度与模块度的关系”实验,得到社团划分结构,即将Zachary网络划分为4个社团,如图4所示. 图4 3WD-PPOC算法对Zachary网络的社团划分结果 (ii)基于Football足球联盟网络实验.Football数据集是经典的社团研究数据集之一,该网络由115个球队的613场比赛抽象而成,如何根据不同球队之间的实力合理划分球队,并合理安排相应的赛事是该实验关注的重点,该网络的原始结构如图5所示. 图5 Football 网络初始社团结构 根据上述“吸收度与模块度的关系”实验,得到社团划分结构,将Football网络划分为6个社团,社团划分的结果如图6所示. 图6 3WD-PPOC算法对Football网络的社团划分结果 (iii)基于Dolphins海豚社会关系网络实验.Dolphin海豚数据集是D. Lusseau等使用长达7 a的时间观察新西兰Doubtful Sound海峡62只海豚群体的交流情况而得到的海豚社会关系网络.这个网络具有62个节点及159 条边,节点表示海豚,而边表示海豚间的接触的频率,该网络的原始结构如图7所示. 图7 Dolphins网络初始社团结构 根据上述“吸收度与模块度的关系”实验,得到社团划分结构,将Dolphins网络划分为4个社团,社团划分的结果如图8所示. 图8 3WD-PPOC算法对Dolphins网络社团划分结果 从图4、图6和图8可以看出,划分后3个数据集的社团结构比较紧密,这说明本文的算法对边界域的节点得到了合理的划分. 为验证本算法的有效性,本文首先将PPC算法(本文算法1)和3WD-PPOC算法进行模块度Q值对比,结果如表3所示. 表3 基于实验数据集的PPC算法和3WD-PPOC的模块度Q值对比 从表3可以看出,在引入吸收度后,Zachary网络社团、Football网络社团及Dolphins 网络社团的模块度均大于没有引入吸收度的模块度,即吸收度的引入可以使延迟决策划分到边界域的重叠节点做出2次决策,使划分后的社团结构更加紧密.基于吸收度的决策结果,对重叠社团的划分好坏有较显著的影响,边界域中的重叠节点的划分更为合理和稳定. 为了进一步验证算法性能,本文将3WD-PPOC算法与经典的Newman算法、GN算法、重叠社团划分算法LFM算法、重叠社团划分最新算法(文献[13]、文献[18])进行模块度值、NMI值比较,结果如表4和表5所示.各算法的时间复杂度如表6所示. 表4 各算法在实验数据集上的Q值对比 表5 各算法在实验数据集上的NMI值对比 表6 算法时间复杂度对比 从表4~表6可以看出:本文所提出的3WD-PPOC算法和Newman算法、文献[18]算法的时间复杂度均为O(n2),其他算法的时间复杂度都高于O(n2),这表明3WD-PPOC具有良好的计算开销.在Zachary网络、Football网络、Dolphins网络中,3WD-PPOC都获得了最高的模块度值,3WD-PPOC的NMI值在3个实验数据集上均在0.8以上,除了在Zachary网络数据集上的NMI值略低于Newman算法外,在其他网络数据集上均优于其他比较算法.Newman算法属于贪心算法的一种,它通过不断迭代更新形成新的社团结构,社团划分结果能较好地刻画社团间的关系.Newman算法与3WD-PPOC的时间复杂度相同,但在模块度方面Newman算法低于3WD-PPOC.在实验数据集上,3WD-PPOC的模块度Q值比Newman算法、GN算法、LMF算法的分别提升了12.4%、10.6%、44.0%,这表明3WD-PPOC比Newman算法在刻画社团内部节点连接稳定性方面具有更好的优势.特别是在Dolphins网络上,3WD-PPOC的NMI值为0.935,远高于其他比较算法,这说明3WD-PPOC算法对该数据集的社团划分精度已达到相当高的程度,划分结构的质量优良. 综上所述,本文所提出的3WD-PPOC算法在处理社团网络划分问题上具有一定优势,在保持较好的处理时间开销下还能有效地对复杂网络节点进行社团划分,且划分出来的社团内部节点具有较好的连接稳定性. 本文将三支决策的思想应用于重叠区域的社团划分,提出了一种基于吸收度的三支决策社团划分算法.该算法根据社团的重要度矩阵和吸收度产生社团重叠区,再通过三支决策建立社团节点与边的界域、正域、负域的对应关系.三支决策思想的引入,有效提高了社团划分的质量.基于真实数据的实验结果表明:本文所提算法能够有效地进行社团划分,F吸收度刻画了社团边界的细节,P吸收度的引入则可以增加边界域重叠节点的归属程度,即提高了社团的模块度.对比其他社团划分算法,本文所提算法在实验网络中能取得较高的划分质量.划分后的各社团结构紧密,这表明该算法对社团重叠节点的划分具有较好的稳定性.下一步将考虑以提高社团的NMI值为目标改进初始重叠社团的划分方法.2.3 PPC算法流程

2.4 3WD-PPOC算法流程


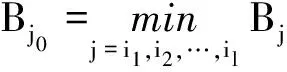
3 算法验证及分析
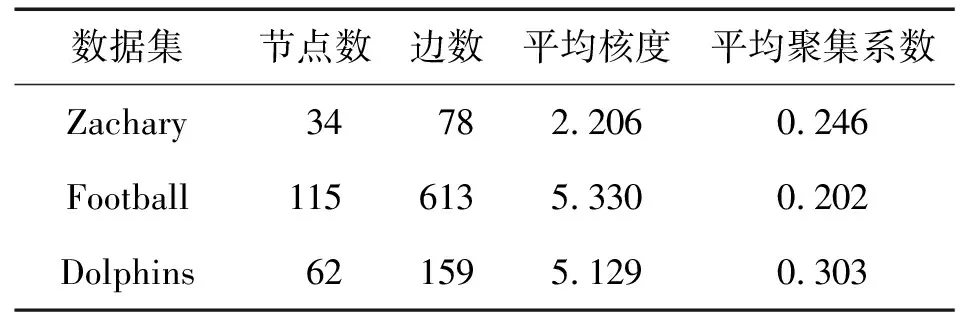
3.1 实验数据与实验环境
3.2 评价指标
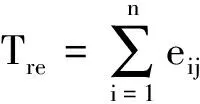
3.3 实验与结果分析


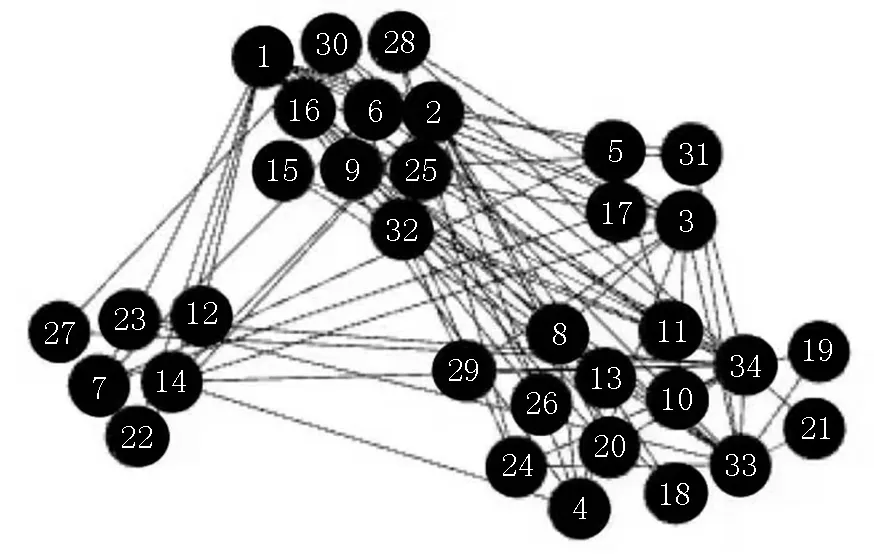


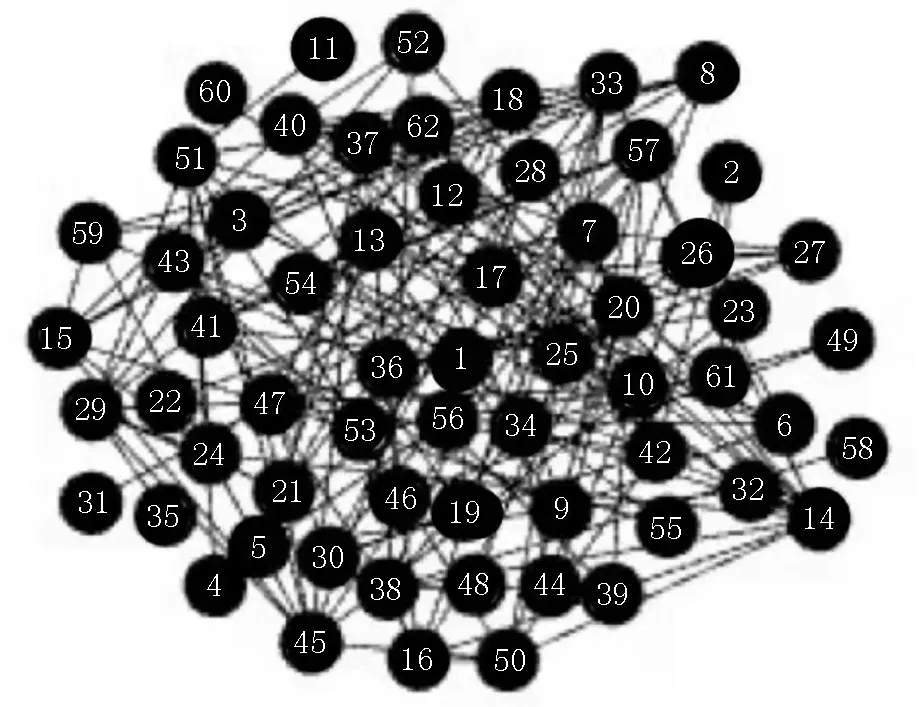
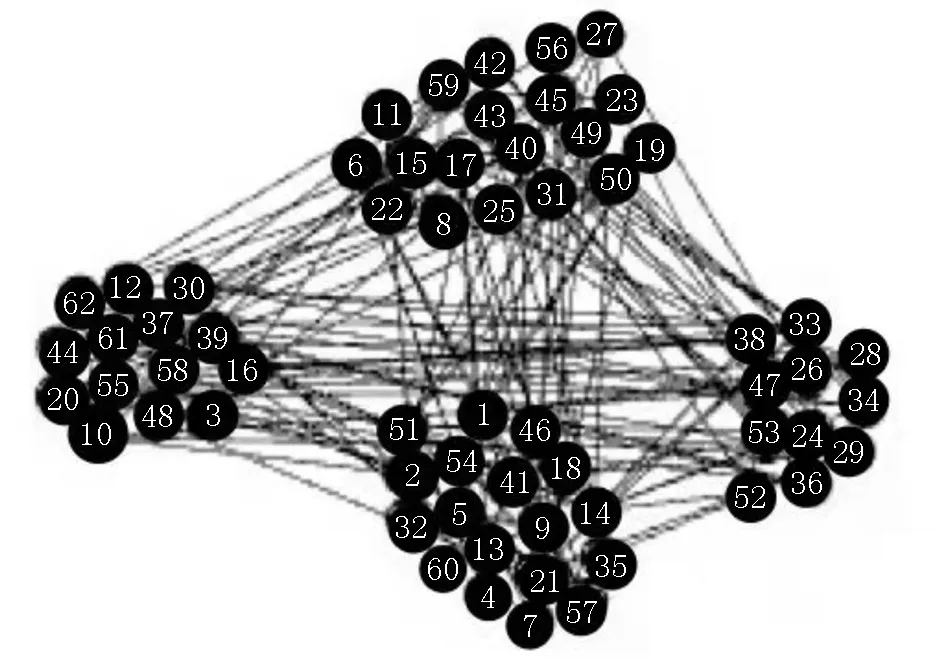
3.4 模块度、NMI值、时间复杂度分析




4 结束语

