结合横向振荡和空间正交的向量血流速度测量

郝鹏慧，杜宜纲，李双双，朱 磊，何绪金

(深圳迈瑞生物医疗电子股份有限公司，广东深圳 518057)

0 引言

在超声临床诊断应用中，血流速度的测量具有十分重要的意义和临床价值。常规的血流成像方法包括彩色多普勒技术、频谱多普勒技术和能量多普勒技术等。随着数字信号处理以及系统软硬件技术的发展，以上技术的成像质量和血流灵敏度都有了很大幅度的提升。但本质上，其核心技术依旧是基于Kasai等[1]在1985年提出的自相关算法，且只能计算血流速度的纵向(沿超声传播方向)分量，然后通过角度校正来估计实际血流速度。但由于人体血流具有复杂的流动形态(如涡流、湍流等)，这就导致角度校正可能会存在很大的误差，进而导致速度估计存在较大偏差，而且以上方法也难以估计血流的实际流向。

为了解决上述血流速度估计方法不能获得实际血流速度大小和方向以及角度依赖等问题，科学家们提出了一系列新的方法来精确计算血流速度和流向[2-4]。其中大部分方法都是通过同时估计血流速度多个方向的分量，然后根据这些分量的大小和方向去计算实际血流速度的大小和方向。也有一部分方法是直接获得实际血流速度的大小和方向。这些方法都可被称为向量血流成像[5]，大致可以分为以下4类[6]：(1)多角度多普勒分析[7-9]，该方法使用多个或一个探头产生偏转角度不同的多个声束，然后分别使用多普勒原理分析计算各个速度分量，最终获得实际的血流矢量。(2)横向声场法[10-15]，使用特定的发射、接收变迹技术，使得发射、接收声场包含纵向和横向两个分量，进而计算血流速度的纵向和横向分量，最终获得实际的血流矢量。(3)斑点追踪法[16-18]，根据超声图像中斑点大小的变化和散射子与扫描速度之间的运动关系，从而计算得到实际的血流矢量。(4)方向互相关分析[19-21]，使用互相关技术和多方向波束合成方法来确定血流速度的方向和大小，从而获得实际的血流矢量。以上方法各有优势，本文主要从第二种方法入手，分别概括了横向振荡(Transverse Oscillation,TO)法和空间正交(Spatial Quadrature,SQ)法的基本原理和成像过程，以及各自的优缺点，并通过对比分析提出了一种结合方法即奇偶振荡(Odd Even Oscillation,OEO)法。该结合方法可以有效地解决TO法存在的成像计算量大以及SQ法存在的相位混叠现象和对噪声灵敏度高的问题。最后，通过实验验证了该结合方法的有效性。

1 横向声场法

1.1 横向振荡(TO)法

传统的彩色多普勒等技术只能测量血流速度的纵向分量，这是因为发射、接收声场只在纵向振动传播，因此血流速度只有纵向分量可以引起回波产生多普勒效应。应用自相关技术也只能计算纵向速度分量，由于横向没有声场振动传播，所以也就无法计算横向的速度分量[8]。如果发射、接收声场不仅在纵向振动传播，也在横向振动传播，那么血流速度的纵向和横向分量都能引起多普勒效应，最终就可以计算得到实际的血流速度矢量，这也是横向声场法的基本原理。根据超声探头变迹方程与焦点区域声场或远场之间的傅里叶关系[22]，可知通过设计特殊的变迹方程(包含两个分离的sinc函数)就可以在焦点区域或远场产生横向声场。根据线性系统理论，应用相同的发射或接收变迹，可以得到相同的目标声场[10]。因此为了简化测量，大部分获得横向声场的方法都是接收变迹。

Jensen等[10,12]提出的TO方法就是其中一种，示意图如图1所示。探头的接收变迹方程包含两个sinc函数，每个sinc函数的宽度为w，两个sinc函数峰值之间的距离为d[23]，那么在焦点区域或远场产生的横向声场的波长大致正比于d，声波的宽度和 w有关[2]。

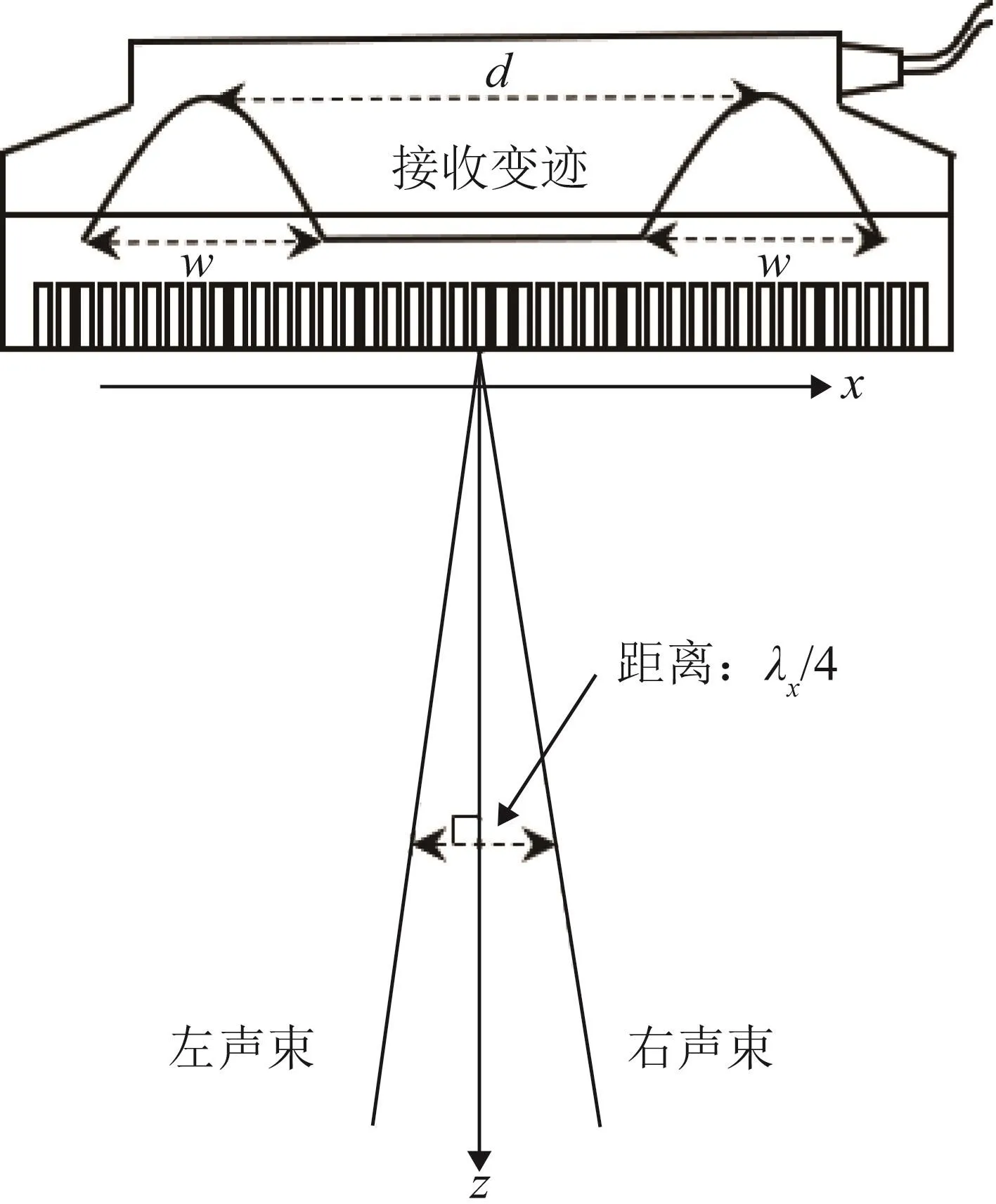
图1 TO方法示意图Fig.1 Principle diagram of TO method

传统的血流速度估计是基于多普勒原理的，方法很多，常用的主要是相位估计法。传统方法需要分别接收同相回波信号和正交回波信号，然后根据自相关算法计算血流纵向速度分量。同样，如果想要测量血流横向速度分量，必须得到横向声场回波的同相信号和正交信号。TO方法通过微微偏转接收声束，以产生两束正交的回波信号(如图1中的左声束和右声束[2])。两束声束之间的距离为横向声波波长λx的1/4，这样两束声束之间的相位差为90°，组成了一对正交信号，可以用于横向速度分量估计，其中：

式中，λx表示横向声场的波长，λ为纵向声场的波长，z为纵向探测深度。另外，由于TO方法需要在空间上进行两次波束合成(左右波束)，所以较传统的彩色多普勒成像，TO波束合成所消耗的计算资源会增加一倍。

使用FieldⅡ[24-25]仿真上述声场，结果如图2所示。FieldⅡ的设置参数为线阵192阵元，频率为5 MHz，阵元间距(pitch)为波长的一半，聚焦距离为20 mm，从图中可知，左右声束的声场均偏离中心位置，相位相差90°，符合理论。

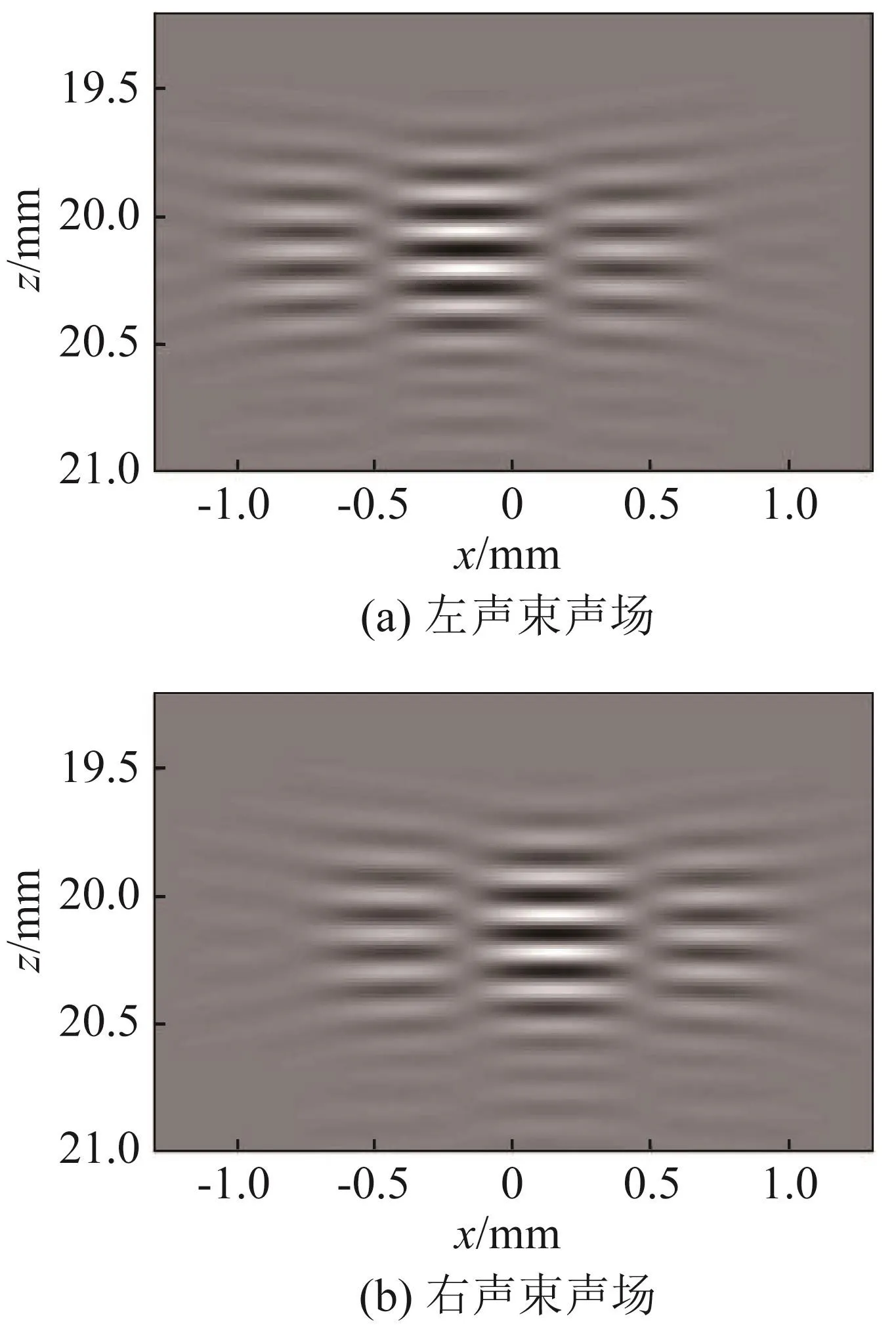
图2 TO方法接收声场图Fig.2 Receiving acoustic field in TO method

假设采集到的左右IQ/RF信号分别为Rleft和Rright，则横向正交信号Rsq和纵向正交信号Rsqh分别为[26]

在这里TO方法使用式(12)提升计算精度，通过复合计算得到(φ1+φ2)和(φ1-φ2)，而不是通过单独计算，这样就降低了计算结果对噪声的灵敏度[12]，同时也避免了当相位大于π时，使用反正切函数计算相位时出现的混叠现象。

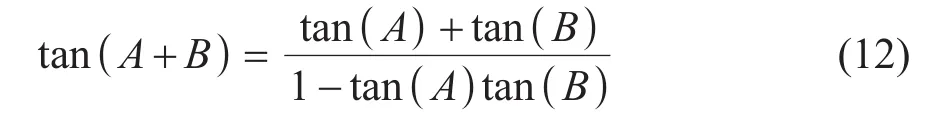
1.2 空间正交(SQ)法

Anderson[11]的SQ法是类似于TO法的另一种方法，其产生横向声场的原理与TO法相同，都是利用特殊的接收变迹实现的，只是产生横向正交信号的方法不同。SQ法的示意图如图3所示。SQ法的接收变迹函数是奇偶两种变迹(希尔伯特变换对)，这样的变迹函数所产生的横向声场同样也是正交的，得到的奇偶信号可以直接用于计算速度的横向分量和纵向分量。值得注意的是，TO法在计算某一点的速度时需要在空间上进行两次波束合成(左右声束)，而SQ法只需要进行一次波束合成(仅需乘以不同的接收变迹值，以得到奇偶信号)，所以SQ法的成像计算量是TO法的1/2。

图3 SQ方法示意图Fig.3 Principle diagram of SQ method

使用FieldⅡ仿真上述声场，FieldⅡ设置参数为线阵192阵元，频率设为5 MHz，阵元间距(pitch)为波长的一半，聚焦距离为20 mm，结果如图4所示。从图4中可知，奇偶声场相位相差90°，与理论值相符。

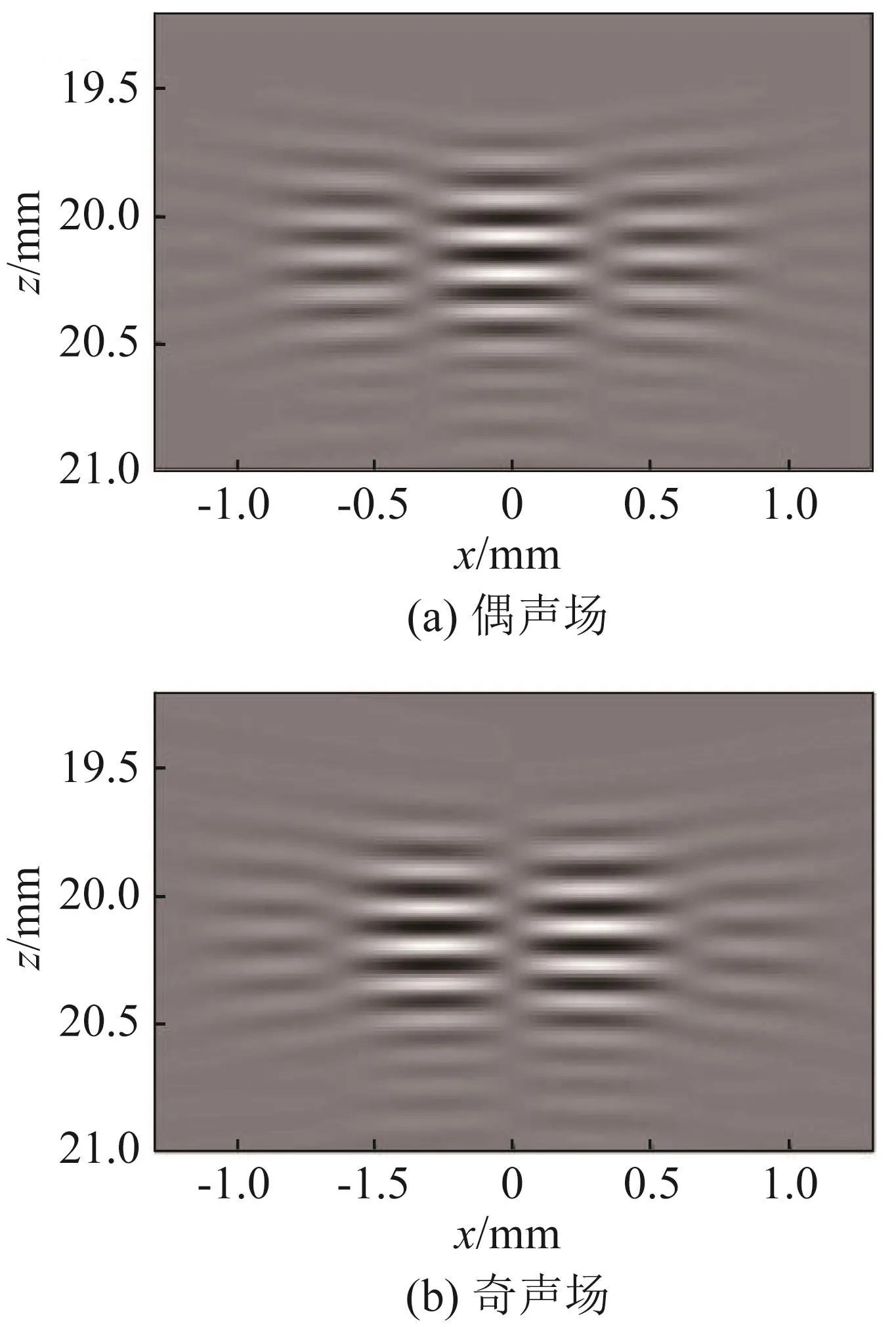
图4 SQ方法奇偶接收声场图Fig.4 Receiving acoustic field in SQ method

假设采集到的奇偶IQ/RF信号为Reven和Rodd，可以表示为[27-29]

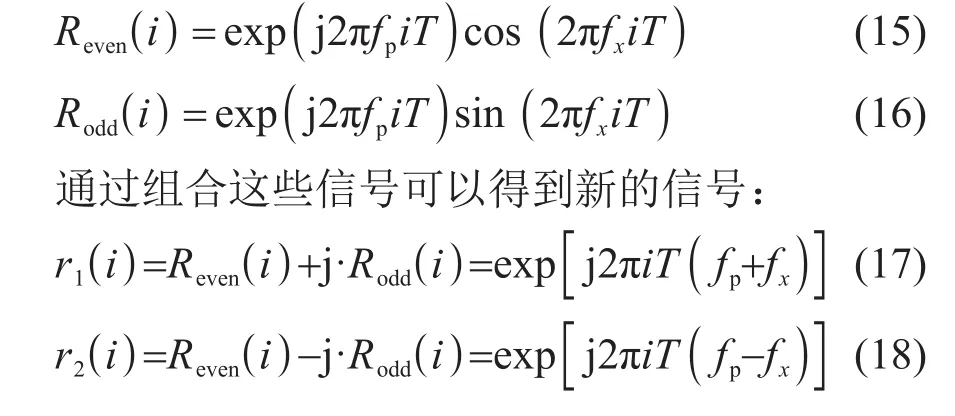
与TO法获得相位信息的方法不同，这里采用了外差解调的方法，即：

由于SQ方法是直接单独计算相位的，所以对噪声的灵敏度特别高，因而也容易出现相位混叠的现象。

1.3 奇偶振荡法(OEO)

通过以上分析可以得知，TO法成像计算量大，但是避免了相位混叠现象，而且降低了对噪声的灵敏度。而SQ方法虽然成像计算量小，却对噪声的灵敏度特别高、容易发生相位混叠，两种方法各有利弊。因此本文提出了一种结合方法，即奇偶振荡法。该方法先利用SQ法进行波束合成得到回波信号，即1.2节中的式(17)、(18)，然后利用TO法进行信号处理计算血流速度，即利用1.1节中的式(12)、(13)、(14)计算速度，既减小了计算量又避免了相位混叠现象，同时降低了算法对噪声的灵敏度。

2 实验研究与结果

实验数据采集设备使用的是迈瑞(Mindray)多普勒超声成像系统Resona 7和线阵探头L11-3U，测量位置为颈动脉，检查模式为颈动脉彩色多普勒模式。因为采集到的数据是未做波束合成的IQ/RF数据，所以TO实验和SQ实验可以使用同一批数据，只是各自的波束合成不同。TO法要使用设计好的接收变迹函数进行左波束和右波束两个波束合成，SQ法则要使用设计好的奇偶接收变迹函数分别进行奇偶波束合成。数据处理流程如图5所示。

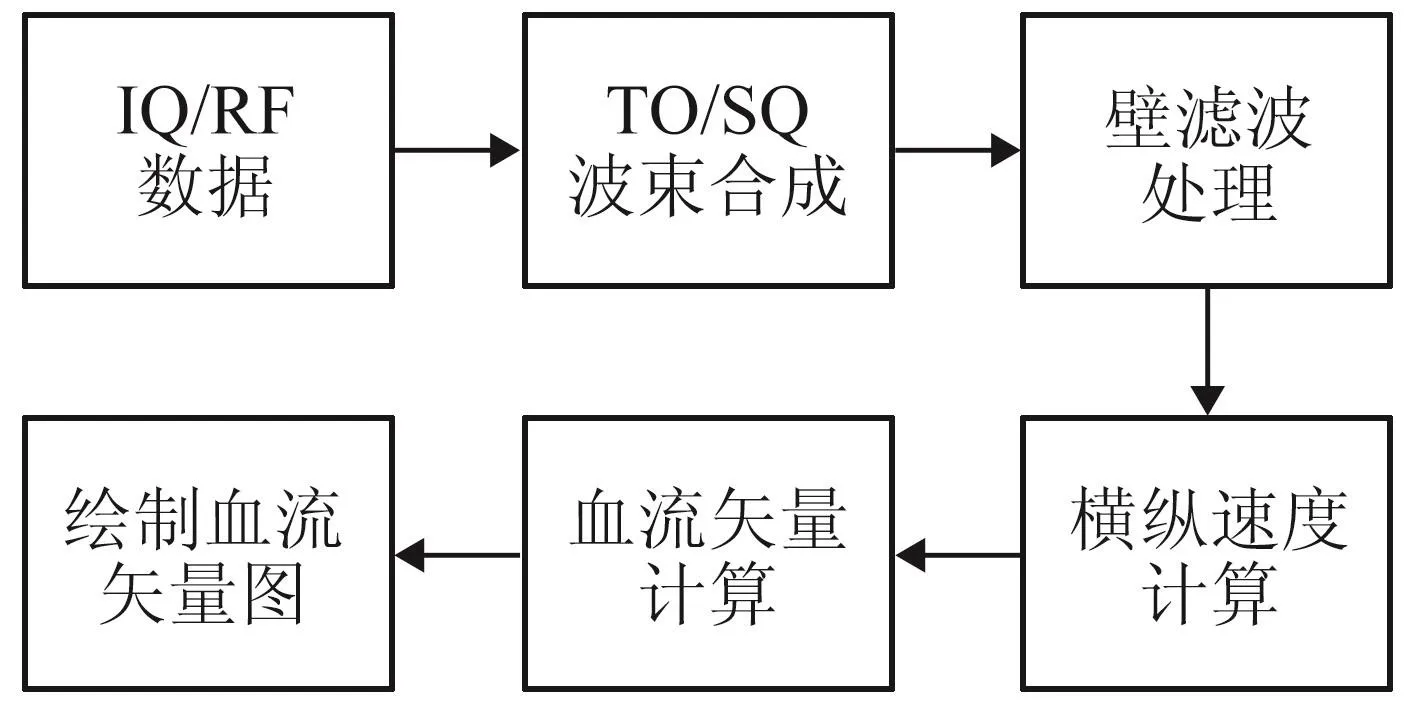
图5 数据处理流程图Fig.5 Flowchart of data processing

对采集到的IQ/RF数据，首先要进行特殊的波束合成(TO/SQ)；之后再进行壁滤波处理，滤除低速运动的血管壁和其他杂乱信号；接着使用1.1中的式(13)和(14)，以及 1.2 中的式(23)和(24)，计算得到每一个探测位置的横纵向速度分量；最后根据各速度分量计算并绘制血流矢量图。

为了验证TO和SQ波束合成的计算量，本文使用采集到的IQ/RF数据，通过后处理的方式分别进行两种波束合成，并统计他们各自计算消耗的时间(计算机配置：i7-8700K CPU，32 GB内存)。结果如表1所示。

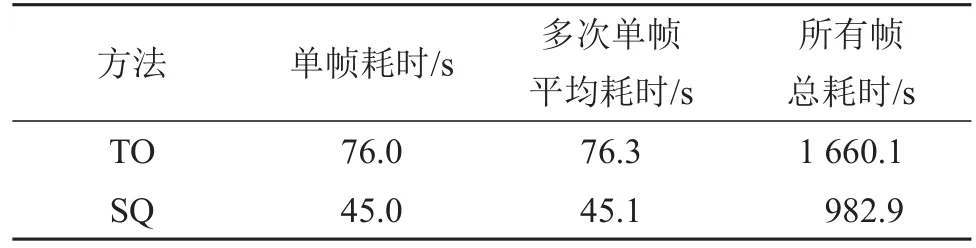
表1 TO法和SQ法波束形成所消耗的时间Table 1 Time consuming for beamforming by TO and SQ methods

为了验证本文提出的奇偶振荡法对成像质量的影响，分别对三种成像结果进行了对比分析。图6、图7和图8分别为TO法、SQ法、OEO法计算得到的血流矢量图叠加上灰阶图像的结果。本次实验总共采集了22帧数据，图6～8中的图像为第2、9、14、20帧的结果。为了观察三种方法计算得到的血流速度在帧之间的变化，同时计算并绘制了所有帧ROI区域内平均血流速度的变化曲线，结果如图9所示。

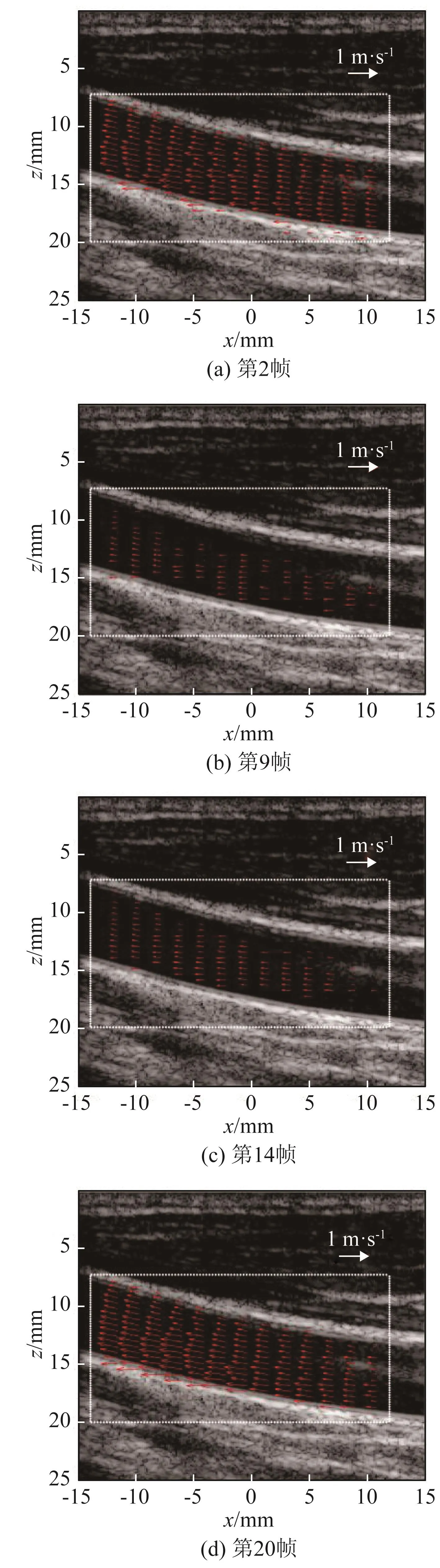
图6 TO方法血流矢量图Fig.6 Vector flow images obtained in TO method

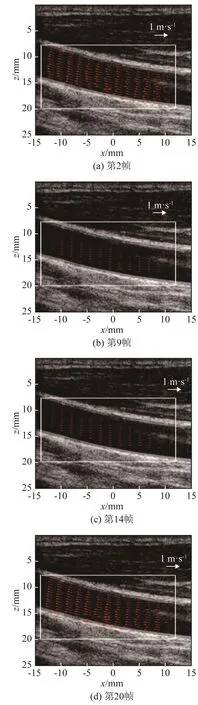
图7 SQ方法血流矢量图Fig.7 Vector flow images obtained in SQ method

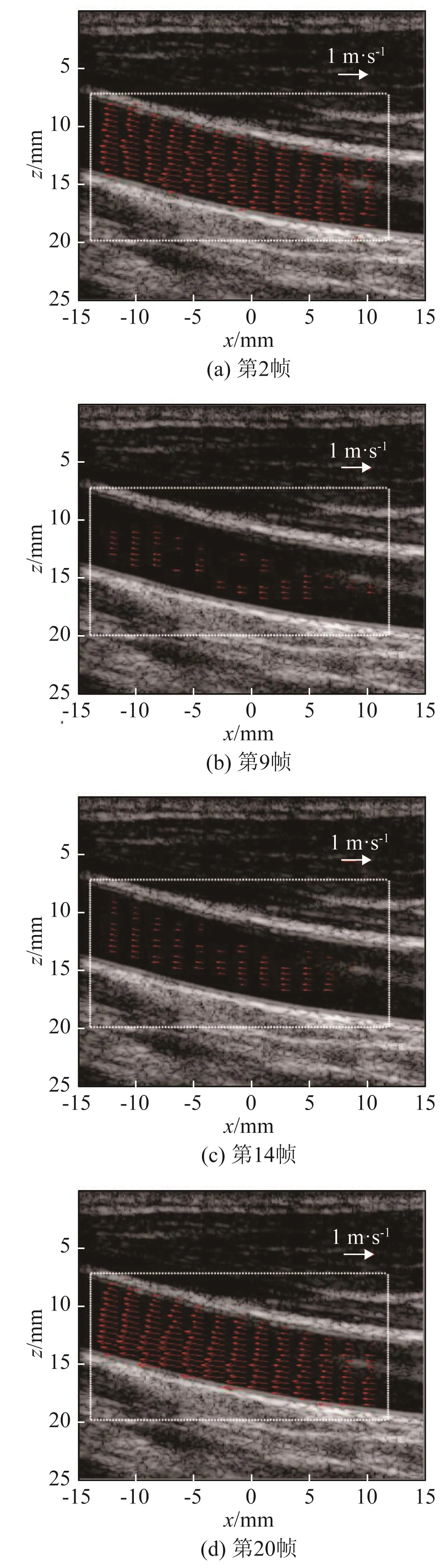
图8 奇偶振荡法血流矢量图Fig.8 Vector flow images obtained in OEO method

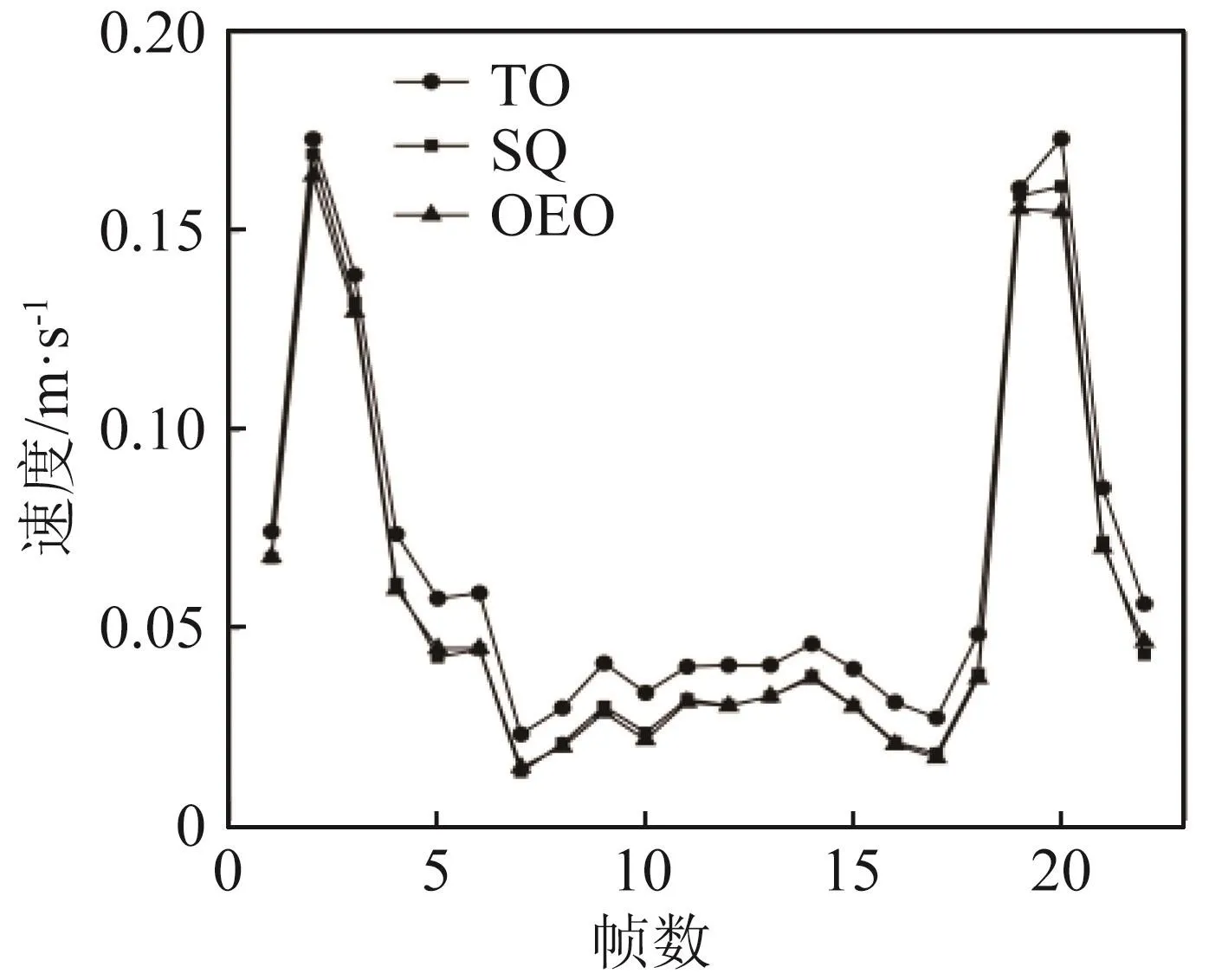
图9 TO、SQ、OEO方法得到的内所有帧的感兴趣区域（ROI）内平均血流速度曲线Fig.9 Average velocities in whole ROI of all frames obtained by TO,SQ and OEO methods

3 分析与讨论

从实验结果来看，TO法的波束合成计算时间(单帧：76 s，全帧：1 660 s)大于SQ法的波束合成计算时间(单帧：45 s，全帧：983 s)，这是由于TO方法需要在空间上做两次波束合成，而SQ只需要做一次。从成像结果来看，TO法不论是在收缩期，还是舒张期，血流矢量都没有出现太大偏差，而SQ法在收缩期时部分长箭头(即高流速)出现反转，原因可能是相位估计时出现了混叠现象，舒张期和TO法类似。本文提出的奇偶振荡(OEO)法成像结果与TO法类似，在舒张期和收缩期都没有出现长箭头反转，即避免了血流速度过高时计算出现的相位混叠现象。另一方面OEO法波束合成所消耗的时间与SQ法保持一致，节省了计算资源，也提高了成像帧率。从所有帧ROI区域内的平均血流速度曲线来看，TO法所获得的速度略微高一点，原因可能是在计算左右波束合成线时横向波长有略微偏差，而SQ法和OEO法在波束合成时不需要计算横向波长。总体来看，三种方法计算得到的血流速度基本保持一致，但是从参考文献[13]可知：SQ法的信号处理过程对噪声灵敏度高。

4 结论

本文提出的奇偶振荡(OEO)向量血流成像方法既有效解决了TO成像法中波束合成计算量大的问题，也解决了SQ法中计算高速血流时出现的相位混叠现象和对噪声灵敏度高等问题，提高了横向振荡向量血流成像的性能。另外该方法还可以扩展应用于凸阵和相控阵超声探头，能够提升超声对全身血管相关疾病的诊断能力。