稀疏贝叶斯学习用于噪声互相关提取格林函数
郭启超,李风华,杨习山
(1.中国科学院声学研究所,北京 100190;2.中国科学院大学,北京 100190)
0 引言
两点之间的时域格林函数(Time Domain Green’s Function,TDGF)可以通过此两点之间环境噪声的互相关函数(Noise Cross-correlation Function,NCF)累积得到[1-3],这为海洋被动声层析[4-6]提供了一种实用方法。该方法的主要问题是NCF累积时间较长。目前,频域白化等预处理方法可以一定程度上改善TDGF的提取质量[7]。空域滤波方法[8-10]是一种可以显著加快TDGF提取的有效技术。此外实验数据表明缩小带宽有助于滤除非扩散噪声干扰,从而提高NCF累积效果。但是,当频率带宽太窄时,传统的反傅里叶变换(Inverse Fast Fourier Transform,IFFT)无法区分TDGF中相邻的到达时间,影响了NCF方法在海洋声被动层析中的应用。
由于NCF方法从环境噪声中估计出少量的TDGF到达时间,该过程可被视为压缩感知(Compressed Sensing,CS)理论中的稀疏重构问题[11-13]。并且由于短时间内TDGF是近似稳态的,因此NCF累积过程可以看做CS中的多观测向量模型(Multiple Measurement Vector,MMV)问题。稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)[14-15]是一种 CS 算法,其通过贝叶斯框架寻找欠定线性系统的稀疏解。SBL与人的思考模式类似,首先假设未知变量服从某种先验分布,然后通过贝叶斯公式对样本数据进行“学习”,不断更新已有认知,最终作出对未知参数的推断。与基于L1惩罚项的CS算法(比如Lasso等)相比,SBL在MMV问题中能自动寻找稀疏度(如TDGF到达时间个数)[16],保持较高的计算效率[17]。在水声学领域,SBL算法已成功应用于波达方向估计[18]、声源定位[19]、水平波数[20]分离方面。
本文利用SBL从较窄频带(带宽为70 Hz)的海洋环境噪声中提取两接收器之间的TDGF到达结构,首先构造了NCF方法的多观测向量模型,其中字典矩阵由傅里叶变换算子构成,观测矩阵由预累积后的频域NCF组成。预累积是指对于给定总快拍数的频域NCF,首先以某个固定的快拍数间隔累积,依次生成每一个观测向量。预累积目的是增强每一个观测向量的信噪比,从而提高SBL的分辨率。为了保证SBL的稳健性,同时预累积快拍数也不能过大。实际使用中应该选取满足分辨率门限的最小预累积快拍数。
联合预累积处理的SBL方法兼顾了噪声提取TDGF的分辨率与稳健性,能够有效获取较窄频带下传统方法无法分辨的TDGF到达时间。仿真与海试实验数据验证了该方法的性能,并且分离得到的到达时间可以用于海水平均声速反演,突破了传统方法提取TDGF到达时间精度的限制。该方法拓展了SBL的应用场景,并且可以与空域滤波方法结合,为自适应选取噪声频段,实现快速海洋被动声层析提供了一种可行方法。
1 理论
1.1 被动TDGF提取
本小节介绍时域格林函数(TDGF)被动提取的基本方法。两点之间的归一化噪声互相关函数(NCF)在频域可以表示为[8]
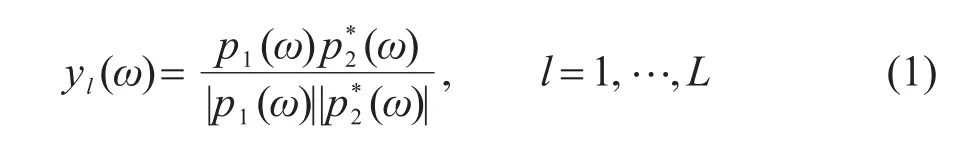
式中:yl(ω)表示一个快拍的频域NCF;L为快拍数;p1(ω)与p2(ω)分别表示两个接收器记录的噪声信号的频域形式;(·)*表示求共轭复数,归一化的目的是通过频域白化的预处理方法消除强频率能量的干扰。利用两条阵列指向端射方向的波束输出互相关代替原本的两个单接收器信号互相关,可以显著地提高每一快拍NCF的质量[18]。对多个快拍的频域NCF进行累积,然后求反傅里叶变换(IFFT),即可获得两接收器位置之间的TDGF[21]:
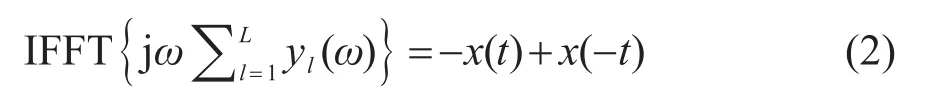
式中:x(t)与x(-t)分别表示因果TDGF与非因果TDGF,它们关于原点对称;jω为相移因子。IFFT方法存在的问题是当频带较窄时,TDGF分辨率低而无法直接应用于声速反演。
1.2 TDGF稀疏模型
本小节将建立频域NCF提取TDGF的稀疏表示模型。给定NCF的总快拍数L,首先将NCF以每ΔL(1≤ΔL≤L)快拍数的间隔累积,重新得到 L′=L/ΔL快拍的NCF。
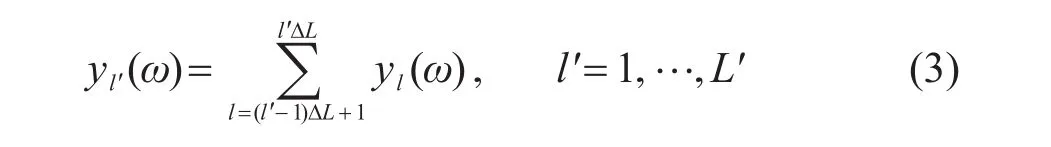
式(3)的作用是调节稀疏贝叶斯学习(SBL)获取的TDGF的分辨率与稳健性(在3.3节中证明)。只考虑因果TDGF,假设每一快拍新的NCF可以看作TDGF与加性高斯噪声的形式,将式(3)代入式(2),并且对式(2)两边进行傅里叶变换,可得到:
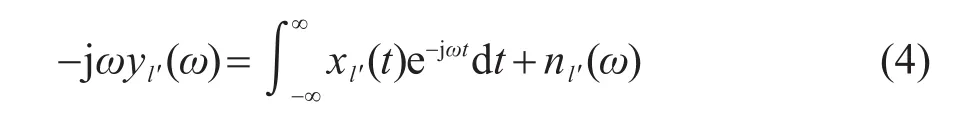
式中:nl′(ω)表示加性高斯白噪声。为了方便表述,用 yl′,xl′与 nl′分别表示 -jωyl′(ω),xl′(t)与 nl′(ω)。令Y=[y1… yL′]∈ CN×L′为观测矩阵,其每一列的观测向量等于预累积后的频域NCF乘上因子-jω,N为NCF包含的频率点数。令 X=[x1… xL′]∈CM×L′,其每一项xm,l′为第l′快拍的TDGF在第m个时间点的复数幅度,并且m=1,…,M,M为TDGF包含的时间点数。此时,将式(4)中的傅里叶变换离散化后,可以得到:

式中:A∈CN×M,为字典矩阵,其每一项 an,m=e-j2π[m(n-1)]/N联系着观测向量中第n个频点与TDGF中第m个时间点之间的傅里叶变换。Z=[n1… nL′]∈ CN×L′, 为 加 性 复 高 斯 白 噪 声 。 假 设N≪M,则式(5)是欠定的。由于稳态的TDGF中只有少量的K个时间点的能量不为0,因此每一快拍TDGF是K-稀疏的,即K≪M。模型(5)为压缩感知框架中经典的多观测向量模型。
1.3 SBL求解模型
本小节简要概括利用SBL求解TDGF模型的方法。假设每一快拍噪声nl′符合均值为0、方差为σ2的 复 高 斯 分 布 , 即 nl′~ CN(0,σ2I), 则 似 然 分布为[17]
选择我院接受的进行超声检查的300例甲状腺结节患者作为案例,对患者采用本院现有的超声量化分级系统实施诊断和评估。本次研究的研究案例均符合要求,经过病理诊断后具备知情权,签署知情同意书。
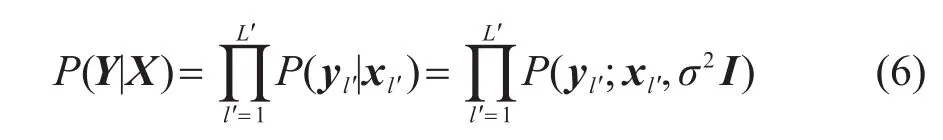
式中:I表示单位向量。假设每一快拍TDGF的幅度服从复高斯先验分布,且不同快拍之间相互独立,则多快拍信号X的先验分布为[17]
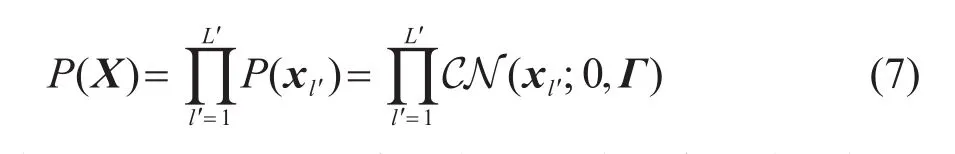
式中:Γ=diag(γ)是一个对角协方差矩阵,其对角元素γ=[γ1…γM]T表示TDGF在每个时间点处的能量。由于TDGF的稀疏性,在算法运行中,大部分时间点的能量γ会趋于0。根据高斯先验与高斯似然分布,得到数据的边缘分布P(Y)也是高斯分布[17]:
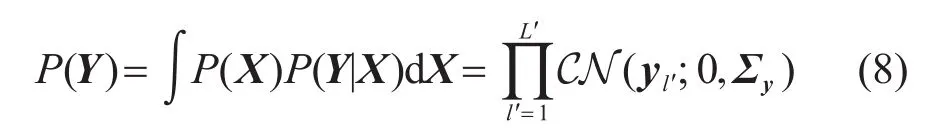
式中:Σy=AΓAH+σ2I表示模型方差。SBL通过最大化数据边缘分布得到TDGF的能量γ[17]:
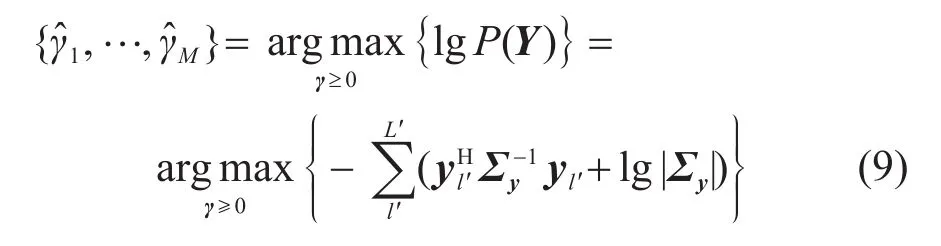
令式(9)中目标函数的导数为0,可得到能量γ的迭代更新解[17]:

式(10)中的每次迭代都需要知道噪声方差的估计值σ2,该变量可以通过每次更新的信号能量计算[17]:
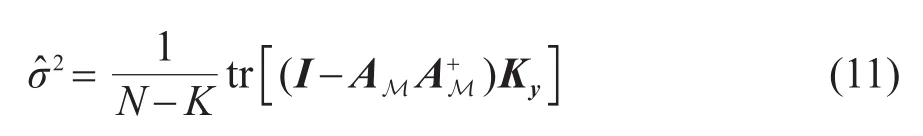
式中:AM为非0位置对应的字典向量的集合,Ky=YYH/L′表示样本协方差矩阵,(·)+表示矩阵的伪逆操作。实际使用中,给定信号能量γ与噪声方差σ2的初始值(例如设置γ=1,σ2=0.1),直到前后两次迭代γ的改善值收敛到一个预设的阈值。此时,信号X的最大后验估计为[17]


2 仿真实验
2.1 仿真环境介绍

图1 实验布放图及声速剖面Fig.1 Layout of the experiment and sound speed profile
2.2 仿真结果
图2给出了不同频带下基于IFFT方法提取TDGF结果,图中粗实线是基于噪声互相关提取的两个接收器之间的TDGF,细虚线是根据将一个接收器作为声源,计算得到的相应接收器之间的信道响应,黑色圆点表示BELLHOP理论计算得到的各条声线到达时间。从图2可以看出,被动TDGF波形与相应的信道响应基本一致,均存在四个明显的到达波包(在图中用1、2、3、4标注),分别对应4条主要声波路径的到达时间,但两者对应波包(尤其是第1、第2个波包)的幅度有区别,这与海面噪声源提取TDGF的理论相符[22]。仿真结果同时也表明,在较宽的频带情况下(20~400 Hz),基于IFFT方法可以获得较为准确的TDGF峰值到达时间,而在较窄频带条件下(110~180 Hz),基于IFFT方法无法分辨TDGF的时间结构。
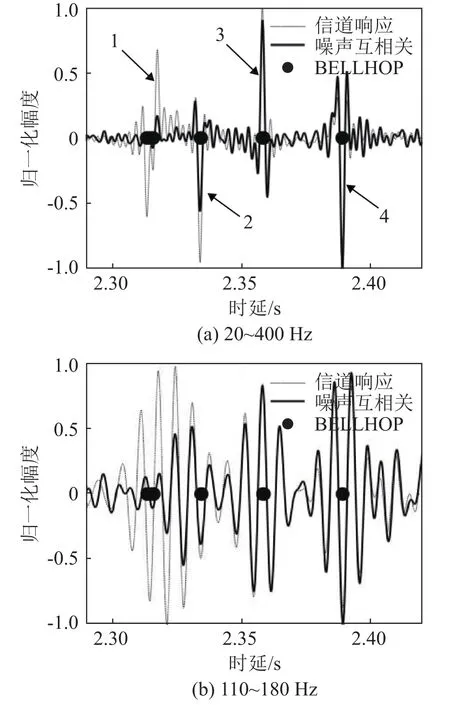
图2 IFFT法提取TDGF与通过将一个接收器作为声源计算的信道响应对比Fig.2 Comparison between the simulated TDGF extracted by IFFT and the channel impulse response obtained by setting one receiver as sound source.
图3给出了基于本文提出的预累积SBL方法得到的TDGF时间结构。在110~180 Hz频段下,给定NCF的总快拍数(1 440),图3中显示了经过不同快拍数ΔL预累积后,基于IFFT(细虚线)与SBL(粗实线)的提取结果,黑色圆点表示计算得到的理论值。从图3可以看出,基于IFFT方法的计算结果不受ΔL影响。对于SBL,随着ΔL增加,TDGF的包络逐渐变窄,当ΔL等于60、90或120时,其第二个包络成功分辨TDGF的第二个到达时间。但是,也不是ΔL越大越好,当ΔL过大时(比如本文中ΔL大于720),基于SBL的估计结果可能与真值产生偏差。
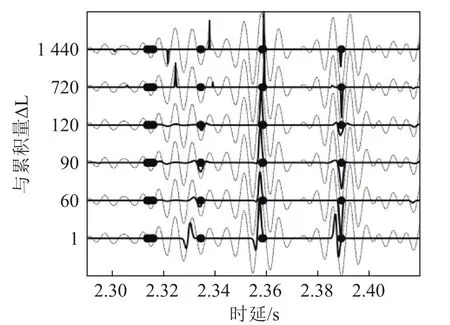
图3 不同预累积量下利用IFFT与SBL从NCFs中提取的TDGF仿真Fig.3 Simulated TDGF extracted from NCFs under different prestacking snapshots by IFFT and SBL
3 海试实验
3.1 海试实验数据介绍
本节利用海试实验数据验证本文提出的预累积SBL算法的有效性。实验于2018年5月在中国南海某海域开展。有两套接收系统同步记录海洋环境噪声,在实验过程中利用温深仪(Temperature Depth sensor,TD)每30 s同步测量一次海水声速剖面。数据处理中,首先将噪声信号分割成若干快拍,每一快拍长度为10 s。利用1.1节中的方法产生每一快拍频域NCF。
3.2 不同频带下提取的TDGF对比
对比不同频带下IFFT与SBL的TDGF提取结果。图4(a)、4(b)分别为20~400 Hz与20~90 Hz频段时、使用IFFT与SBL,从720快拍(2 h)NCF中提取的TDGF,散点为使用BELLHOP根据实测水文仿真的TDGF到达时间理论值。当频段为20~400 Hz时,IFFT与SBL中均存在4个明显的独立波包(在图中分别用1、2、3、4标注),分别与Bellhop计算得到的4个到达时间相吻合。当频段为20~90 Hz时,IFFT无法分辨各到达时间,而SBL仍然能够较好分辨各到达时间。
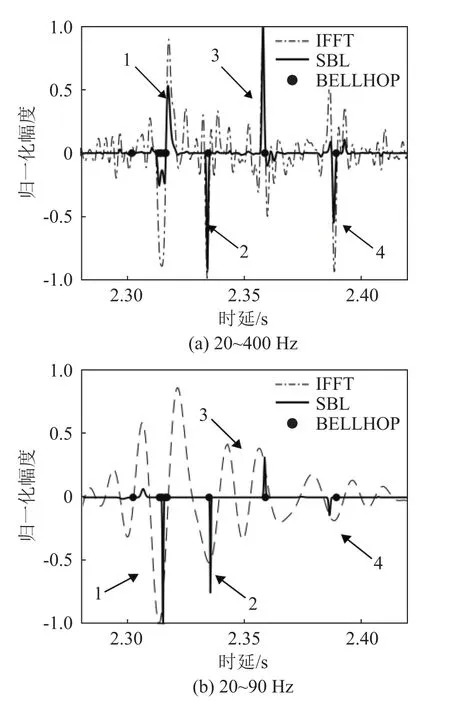
图4 不同频段的海洋环境噪声中提取的TDGFFig.4 TDGF extracted from ocean ambient noise in different frequency bands
3.3 预累积处理对SBL提取TDGF的影响
本节讨论预累积量ΔL与基于SBL方法提取TDGF的分辨率与稳健性之间的关系。图5分别给出了经过不同ΔL预累积之后,基于IFFT(细虚线)与SBL(粗实线)方法得到TDGF,信号频段为110~180 Hz,散点表示BELLHOP理论值。数据处理结果与仿真结果一致,IFFT均无法分辨TDGF的前两个到达时间,SBL在ΔL为30或120时,可以较好地估计第二个到达时间(包络的波谷位置)。而当ΔL=1(不进行预累积)或ΔL=720(全部预累积)时,估计结果分别出现了分辨率低与偏差大的问题。
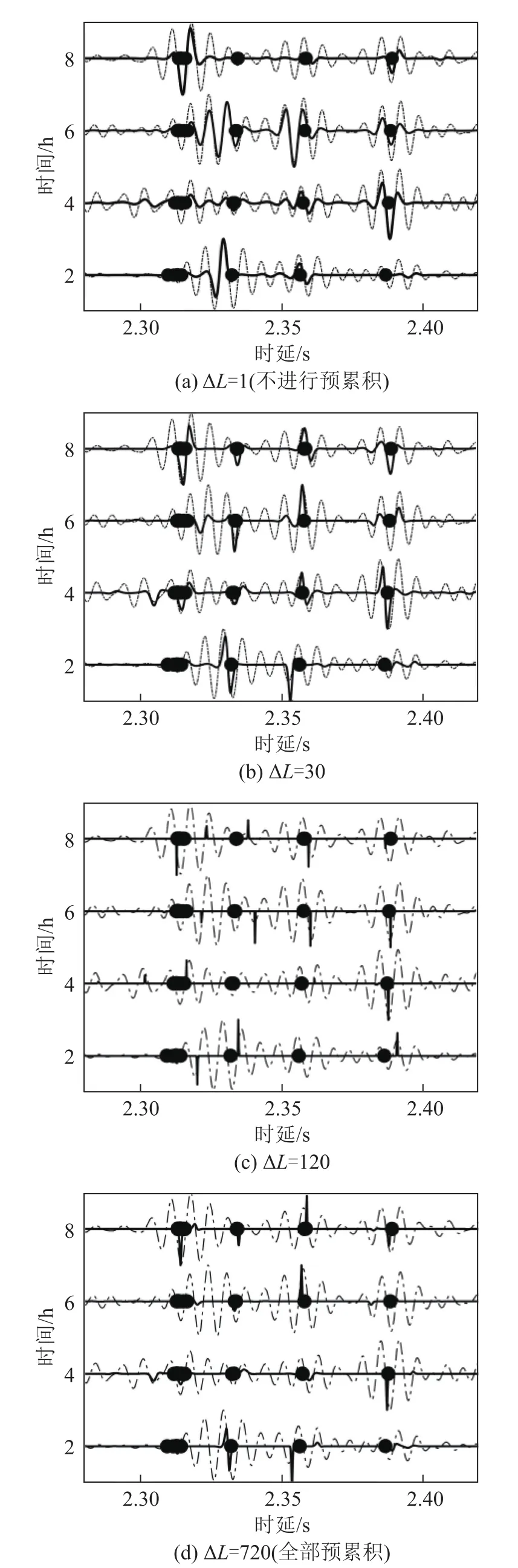
图5 不同预累积量时,利用IFFT与SBL从海洋环境噪声中提取TDGF的结果Fig.5 The results of TDGF extracted from ocean ambient noise with different ΔL by IFFT and SBL
定义TDGF的包络宽度(Band Width,BW)为其Hilbert包络绝对值下降3 dB时两个到达时延的差值:

图6为经过70 h平均后,SBL估计的第二号到达时间在包络宽度内的最大误差随ΔL的变化情况。随着ΔL的增大,最大误差先减小后增大。原因是SBL估计的TDGF的分辨率与稳健性是一对相反关系,即随着ΔL的增大,TDGF的分辨率提高但稳健性降低。当ΔL较小时,分辨率的提高起主要作用,也就是说,包络变窄使得TDGF的“随机误差”范围变小;而当ΔL较大时,稳健性的损失起主要影响,即包络中心位置与真值之间偏差使得TDGF的“系统误差”增大。图6同时也说明,通过选取合适的ΔL,SBL可以在分辨率与稳健性间进行折中。
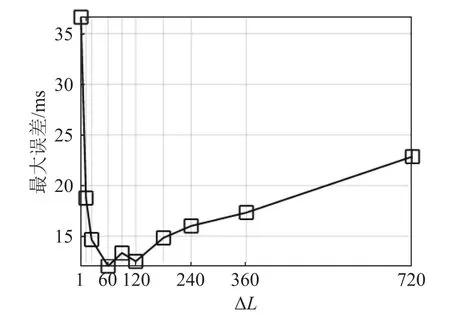
图6 70 h平均的SBL估计的TDGF第二号到达时间的最大误差随预累积量的变化Fig.6 Variation of the 70 h averaged maximum error of the second arrival time of TDGF estimated by SBL with differentΔL
进一步讨论预累积量ΔL对基于SBL方法提取TDGF的分辨率与稳健性的影响。SBL假设待估计的稀疏向量中的每个元素都服从一个均值为0、方差为γ的高斯分布。在算法运行中,γ中的绝大部分值会变成0(无噪情况下)或者趋于0(有噪情况下)。在给定总快拍数条件下,一方面,预累积快拍数越多,则每一个观测向量的信噪比越高,则非真值位置的能量越容易趋于0,也可以理解为数据信噪比越高,则SBL的“学习”效果越好,越能确切地将靠近真值附近的非真值点的能量置0,表现在波形上就是包络窄,分辨率高;另一方面,若预累积后的各观测向量已经具有较好的信噪比,那么将多个观测向量组成矩阵输入SBL,比简单地累积为一维的向量效果好。原因是:(1)在稳态情况下,不同观测向量之间有共同的稀疏性[23],简单累积为一维向量会“浪费”共同稀疏性的约束,导致估计的非0位置不稳定。(2)预累积会导致样本协方差矩阵维度减小,估计的噪声方差不稳定(式(11)),而噪声方差又会影响SBL对非0位置的估计(式(10))。因此在实际使用中,应该首先根据频带范围确定分辨率的最低门限,然后选取达到分辨率门限的最小ΔL。
3.4 结果
图7给出了使用IFFT与SBL从每2 h NCFs中提取一次TDGF,共计70 h的提取结果,其中黑色点线为利用实测声速剖面通过BELLHOP软件计算的TDGF到达时间理论值,噪声数据的频段为110~180 Hz,SBL的预先累积量ΔL设置为12,为了尽可能提高SBL的稳定性,减小声速反演误差,ΔL的选取小于图6中的最优解60。从图7可以看出,基于SBL方法可以清晰看到4条声线的到达时间结构,而IFFT只能看到较宽的三个区域,无法准确分辨各条声线的到达时间,其原因是基于IFFT的提取方法对应的不同声线信号之间发生“混叠”。

图7 使用IFFT与SBL从海洋环境噪声中提取的共计70 h的TDGF结果Fig.7 The results of TDGF extracted from 70 h ocean ambient noise by IFFT and SBL
图8为利用SBL估计TDGF的第二条声线到达时间反演得到的海水平均声速与TD实测的海水平均声速的比较,二者之间的均方根误差为0.6 m·s-1。实验结果证实了相比于传统方法,预累积SBL提取的TDGF可以更准确地获取较窄频带下的声线到达结构。
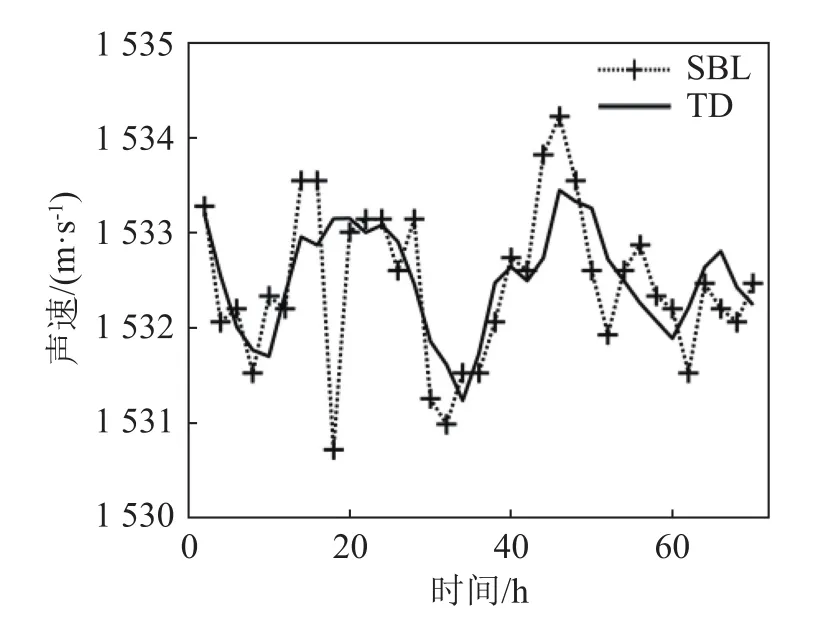
图8 利用SBL提取的TDGF第二号到达时间反演海水平均声速与温深仪实测声速对比Fig.8 Comparison between the averaged sound speed inverted by the second TDGF arrival time estimated by SBL and the measured sound speed by bathy thermograph
4 结论
为解决较窄频带下传统的噪声互相关提取TDGF方法时域分辨率低的问题,提出了一种基于SBL的噪声互相关TDGF提取方法。首先建立了TDGF的稀疏模型,其中字典矩阵由傅里叶变换算子组成,观测矩阵由频域噪声互相关函数组成。然后提出利用预累积处理来折中SBL估计TDGF的分辨率与稳定性。仿真与实验数据处理结果表明:通过选取合适的预累积量,基于SBL方法可以准确、稳健地从较窄频带的海洋环境噪声中获取TDGF的时间到达结构,有效克服传统方法时间精度低的问题,为之后开展自适应挑选噪声频段,实现快速被动声层析提供了一种可行方法。

