声流条件下超声空化气泡分布研究

孙世琪，刘 斌，付 汨，吴 雪，王 晶

(北京工商大学人工智能学院，北京 100048)

0 引言

超声空化效应是指声波在液体中传播时，声压产生周期性交替变化，在液体中形成局部的压缩相与膨胀相，溶于液体中的微小气泡核在膨胀相生长，在压缩相被压缩直至溃灭的一系列动力学过程。在超声空化过程中会产生高温、高压以及局部微射流等极端现象，为物料破碎、化学催化等过程提供了有利条件，在化工、生物、医药卫生以及仪器清洗等方面有广泛应用[1-3]。由超声空化所引起的声化学反应活性取决于空化的分布范围和强度，超声空化的分布范围越广、强度越大，声化学反应活性越强。超声空化作为一种高效提供能量的方法，如何增强超声空化的分布范围，提高声化学反应效率和声能利用率，成为现阶段超声研究的重要内容。

当超声功率较小时，超声波在料腔介质中满足小振幅传播特性，空化气泡聚集在声源附近，空化分布范围极小，影响了声化学反应效率，限制了超声空化的大规模工业应用。针对这一问题，Klíma等[1]研究了反应料腔内的声强分布并对料腔形状尺寸进行了优化设计；马立康等[2]研究了液位和超声功率对超声空化强度的影响。随着超声功率的增大，声波振幅增大，声波在介质中呈现非线性传播特性，介质吸收声能并转化为动能，产生稳定的声致流动现象[4]。Moussatov等[5]发现在声强较大时，声源附近的锥形气泡群会形成轴向射流；Rubinetti等[6]提出了不同参数、料腔几何形状和材料的声流数值求解模型；刘继伟[7]研究了声流效应和驻波声流场中悬浮颗粒的运动情况。由此可见，现有研究大多只对超声空化或声流现象进行了单方面的研究，缺少声流现象对超声空化场分布影响的相关研究。

针对现有研究的不足，本文以柱形腔体中的声场为对象，研究声流条件下超声空化气泡的分布情况，在理论分析的基础上，利用仿真分析和实验研究，初步探讨了较大功率超声作用形成声流时的流场分布特性以及声流效应对超声空化空间分布特性的影响，进而对比研究有、无声流现象时的空化效应的区域增强效果，以期从空化效应的增强和优化的角度，对如何提高声化学反应效率及超声声能的利用进行探讨，为超声空化工程在工业领域中的进一步深入应用提供相关的理论分析和实验参考。

1 声流效应形成机制

在较大振幅条件下，声传播所形成的非线性效应是导致声流现象的原因，声场中声场量的一阶微小项提供周期分量，二阶微小项提供直流分量，根据声流现象中各个物理量的不同扰动级数，将流体介质中p、v和ρ的时间平均值分为直流成分和周期性成分[8]：

其中：p为流体总压力，p0为流体初始压力，p1为声压；v为流体速度，v0为流体的宏观流动速度，v1为介质粒子在平衡位置做往复运动的速度；ρ为流体密度，ρ0为流体初始密度，ρ1为受超声作用后流体密度的改变量。

流体运动过程中的质量守恒方程与N-S方程分别为[4]

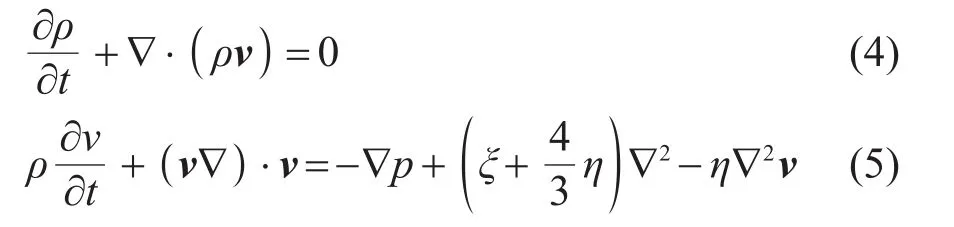
其中：ξ和η分别为流体的容变黏度和切变黏度。

将声场量转化为流场量，需要对式(4)、(5)进行时间平均处理，保留二阶微小项得到时间平均后的质量守恒方程与N-S方程为[8]

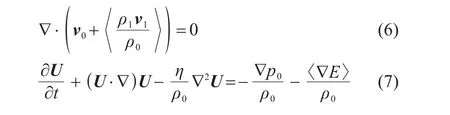
式(7)等号右侧为驱动单位质量流体介质流动的驱动力。当只有声场作用时∇p0=0，诱导流体形成声流现象的驱动力F为声辐射力，大小等于空间声场的能量密度差[8]：

在不忽略二阶微小项的条件下，只要声场中存在能量密度差，就有作用于流体中的力使流体流动。

2 声流速度场仿真分析

2.1 声流流场的有限元模拟

结合上述诱导声流形成的声辐射力分析，应用有限元方法可以获得料腔内各区域声流的速度大小与方向，进而预测空化气泡的运动和分布情况。

根据实验材料中提供的圆柱形料腔声场的几何模型，采用二维轴对称模型；变幅杆端部为声源，变幅杆浸入溶液深度为10 mm；声场传播介质为水，材料密度为1 000 kg·m-3，声速为1 480 m·s-1；由于声波波长远大于料腔壁厚，且水与空气的声阻抗相差很大、与有机玻璃的声阻抗相差很小，所以声学边界设定的条件是变幅杆侧壁与水交界面为硬声场边界，其余均为软声场边界；以声辐射力作为流体的动力输入条件，流体边界设定的条件是水与空气交界面为开放边界，其余均为无滑移边界。由于流体网格的尺寸要求远大于声学网格，采用共用流体网格，网格数量为2 265～3 203，网格划分的最小单元为0.09 mm，满足声学网格需求。

(1)采用压力声学频域接口和稳态研究对料腔内声能密度分布进行求解。由于声流的产生是由于声传播的非线性效应所引发，需考虑流体黏性的影响，因此添加一个用于表示黏性耗散的偶极子源项qd[6]：

其中：c为介质中的声速，ω为声源的角频率。

通过得到的声能密度求解流体在轴向和径向所受声辐射力的分量，已知平面圆形声源在径向的质点速度约为轴向质点速度的1%[6]，声辐射力径向分量可以忽略，因此只需求解声辐射力的轴向分量即流场中流体的体积力。

(2)根据计算得到的体积力，采用层流接口和稳态研究对料腔内声流速度场进行求解，得到速度分布的云图。

2.2 声流速度分布特性分析

2.2.1 功放电流对声流速度分布特性的影响

功放电流分别为40、80和120 mA时，液位高度为70 mm、内径为60 mm的圆柱料腔内声流的速度分布如图1所示，距变幅杆端部不同轴向距离处的声流速度值如图2所示。

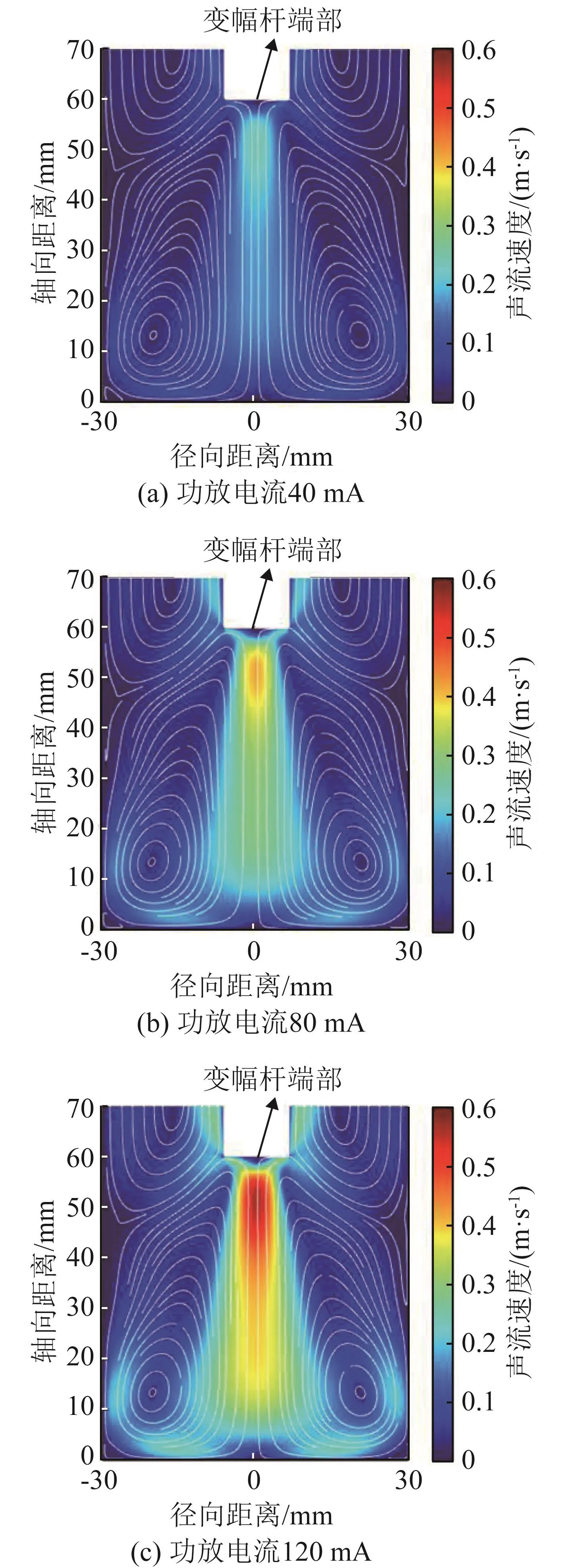
图1 不同功放电流下圆柱料腔内声流速度分布Fig.1 The acoustic flow velocity distribution in the cylindrical cavity under different power amplifier currents

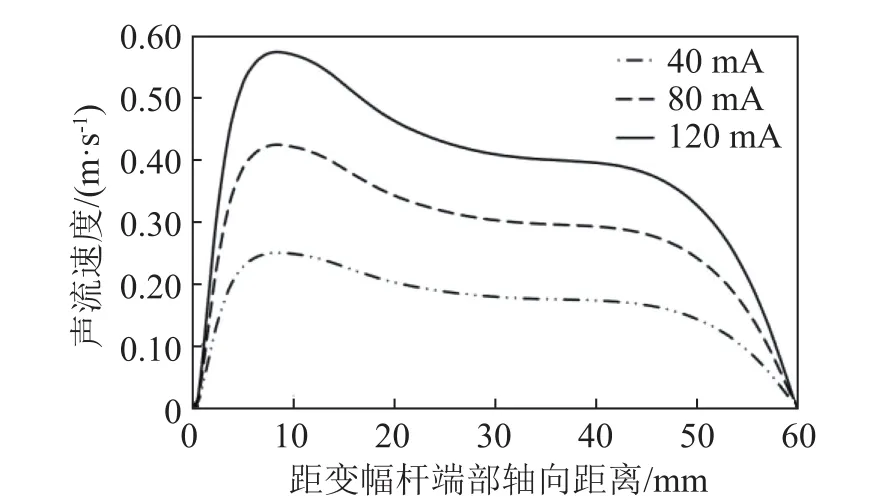
图2 不同功放电流下圆柱料腔轴向的声流速度分布Fig.2 Acoustic flow velocity distribution in the axial direction of cylindrical cavity under different power amplifier currents

由图1可知，流体从变幅杆端部出发形成射流，沿着轴向运动，在接触料腔底部时运动方向发生偏转，沿着料腔底部向壁面运动，最终在变幅杆浸入端两侧和料腔底部与侧壁交界处形成稳定的往复运动的涡流。由图2可知，料腔内声流速度值在变幅杆端部附近随着轴向距离的增加急速增大，在距变幅杆端部约8 mm处声流速度达到最大值，然后随着轴向距离的增加而逐渐减小，在液面、料腔底部以及侧壁处速度大小趋近于0。在流体运动过程中，声辐射力的轴向分量使其加速，液体的粘滞力则作用相反，使得流动速度逐渐减小；流体远离变幅杆端面位置后，声辐射力的轴向分量逐渐减小，与流体粘滞力相同时，流体达到最大速度，此后流体做减速运动。由图1、2可知当液位高度相同、超声功率不同时，料腔内同一位置处的声流速度值随着功放电流的增加而增大，因此声源的输入功率能够影响声流速度的分布。

2.2.2 液位高度对声流速度分布特性的影响

功放电流为80 mA，液位高度分别为50、60和70 mm时，内径为60 mm的圆柱料腔内声流速度分布如图3所示，距变幅杆端部轴向不同距离处的声流速度值如图4所示。由图3、4可知，超声功率相同、液位高度不同时，距变幅杆端部相同距离处的声流速度也不同；由图4可知不同液位高度下的声流速度极值随着液位高度的增加而增大，因此圆柱料腔中不同的声场几何形状可影响声流速度分布。

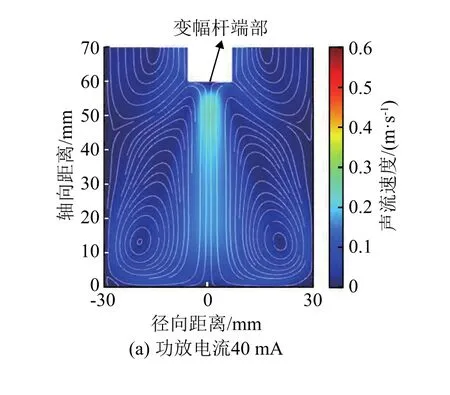
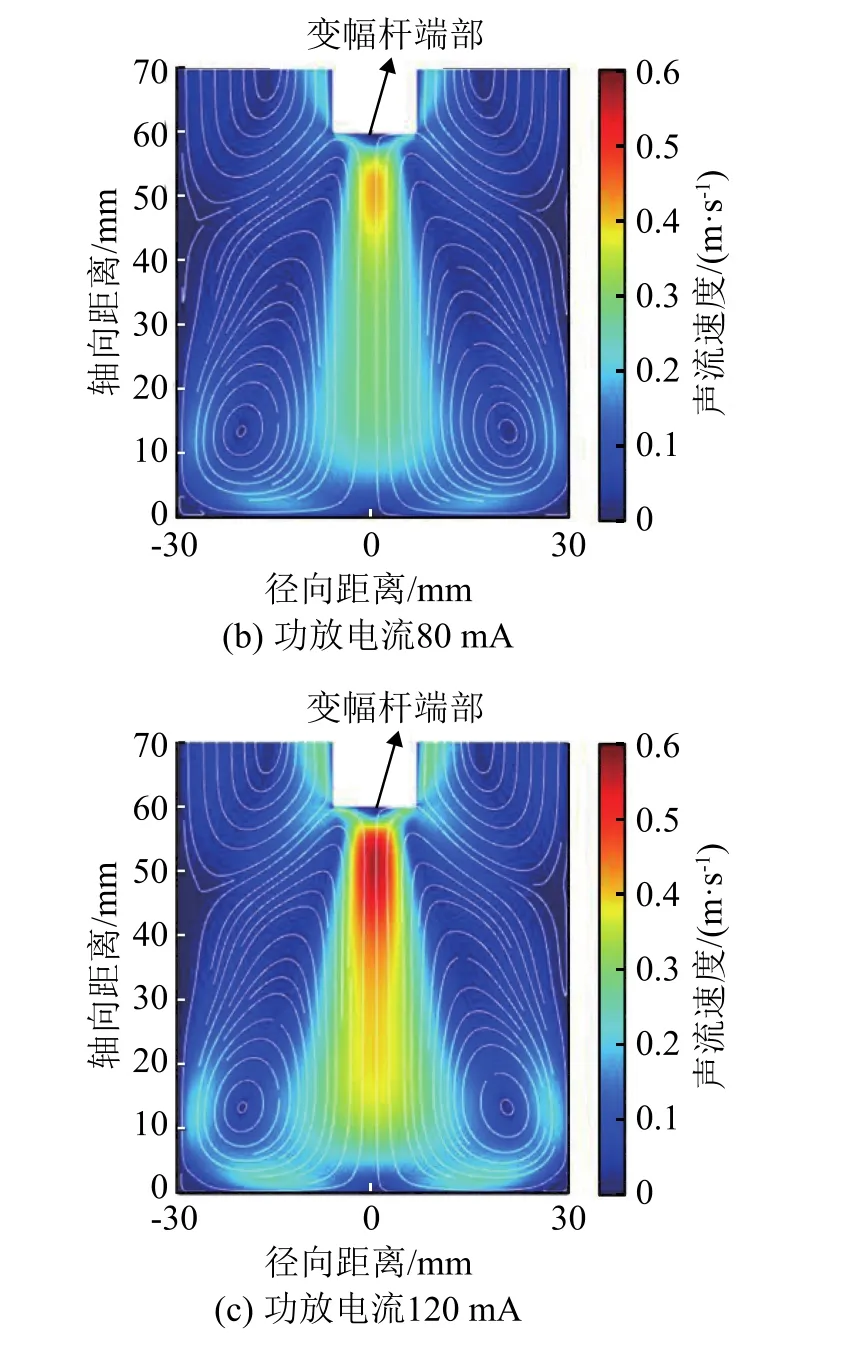
图3 不同液位高度下圆柱料腔内声流速度分布Fig.3 The acoustic flow velocity distribution in the cylindrical material cavity under different liquid level heights

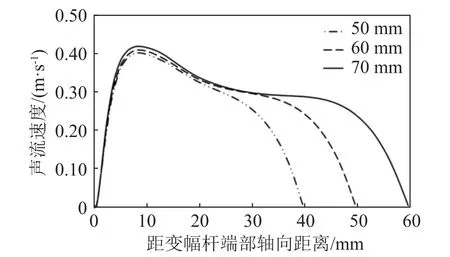
图4 不同液位高度下圆柱料腔轴向的声流速度分布Fig.4 Acoustic flow velocity distribution in the axial direction of cylindrical cavity under different liquid level heights

根据仿真结果可以预测，在变幅杆端部附近的空化气泡能够在声流的作用下沿着轴向运动，并在容器底部发生偏转，实现较大程度的扩散，增大声 化学反应区域的面积；当输入功率和液位高度不同时，柱形料腔中声流速度分布不同，因此在不同的声场条件下，空化气泡溃灭前的运动距离和分布范围也存在差异。声流速度越大的声场几何模型中，空化气泡运动的距离越远。

3 声致化学发光实验

3.1 材料与仪器

3.1.1 实验材料

质量分数为0.1%的氢氧化钠与0.01%的鲁米诺溶于超纯水(含气量为0)配制成的鲁米诺水溶液试剂。料腔容器采用内径为60 mm、壁厚为2 mm的圆柱形有机玻璃筒，玻璃筒一端开口、一端封闭。

3.1.2 实验仪器

实验采用频率为20 kHz的变幅杆式超声换能器，变幅杆端的辐射端面直径为13 mm。超声波发生器的额定功率为200 W，与换能器配套，频率20 kHz，频率自动跟踪。照相设备采用尼康D90单反式数码相机。

3.2 实验方法

超声空化气泡溃灭时产生的能量使水电离出的羟基能够与鲁米诺试剂发生反应，发出肉眼可见的蓝光。这种现象称为声致化学发光(Sonochemiluminescence,SCL)，配合长时间曝光拍摄，可以明显观察到反应料腔内空化场的分布情况[9]。

在暗室条件下，向内径为60 mm的柱形料腔注入不同液位高度的鲁米诺试剂，变幅杆浸入液面的深度为10 mm，观察不同电流条件下功率超声处理时的鲁米诺发光现象，采用数码相机曝光拍摄，曝光时长为5 min，采用水浴槽控制温度，保持温度恒定。实验测试系统装置如图5所示，图中r为圆柱形料腔半径，d为变幅杆式超声换能器浸入深度，H为料腔内液位高度。

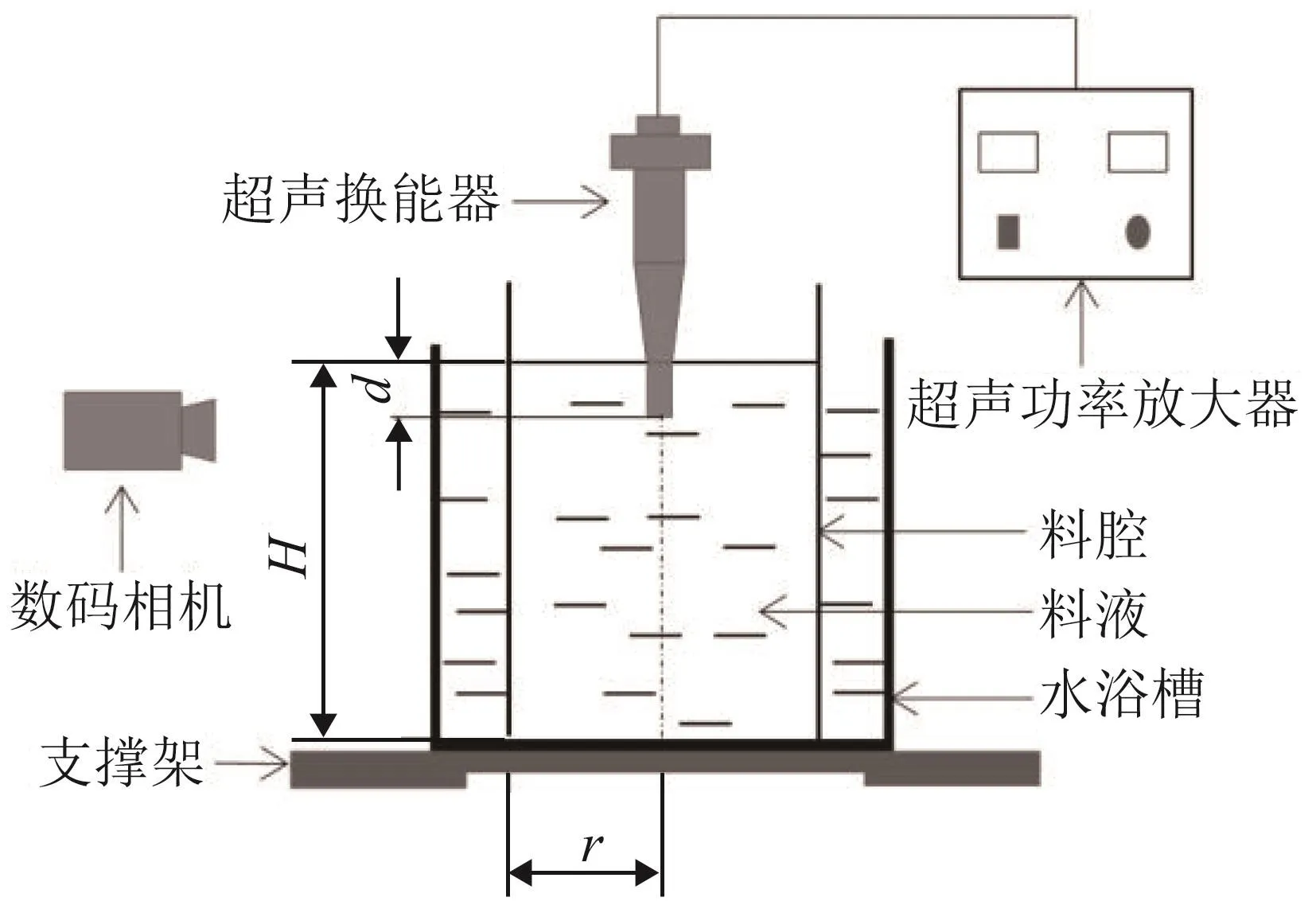
图5 实验测试系统简图Fig.5 Schematic diagram of the experimental test system

3.3 空化气泡分布的SCL图像分析

3.3.1 功放电流对空化气泡分布的影响

功放电流分别是40、80和120 mA时，内径为60 mm、液位高度为70 mm的圆柱形料腔内空化气泡分布的SCL图像如图6所示。由图6可知，在同一液位高度下，超声功率较高时料腔声场中出现声流现象。对图6(a)～6(c)进行二值化求解[10]得到空化面积占比分别为14.02%、20.92%和28.16%，功放电流120 mA时的空化面积占比，比40 mA时提高了100.86%。因此料腔形状尺寸一定时，声流对空化面积有明显的增效作用，且超声功率越高，空化气泡分布范围越大，空化气泡由变幅杆端部区域沿轴向扩散至料腔底部以及其他区域。

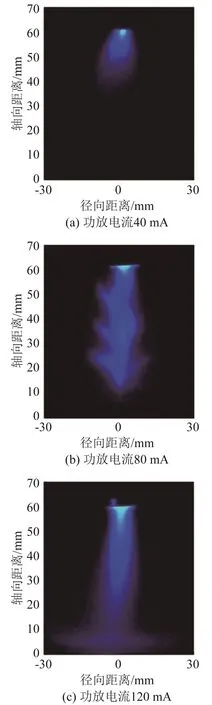
图6 不同功放电流下圆柱料腔内空化气泡分布的SCL图像Fig.6 SCL images of cavitation bubble distribution in the cylindrical cavity under different power amplifier currents

3.3.2 液位高度对空化气泡分布的影响

功放电流80 mA，液位高度分别为50、60和70 mm时，内径为60 mm的圆柱料腔内空化气泡分布的SCL图像如图7所示。图7(a)表明液位较低时，空化气泡在声流的作用下从变幅杆端部区域沿轴向运动扩散，大部分气泡在运动过程中沿径向扩散，一小部分气泡再继续沿轴向运动时发生溃灭；图7(b)表明一部分气泡运动至料腔底部时才发生偏转，向侧壁方向扩散；图7(c)表明液位足够高时空化气泡只沿变幅杆轴区域运动扩散，气泡在运动到料腔底部之前就已溃灭，空化效应区域较为集中。对图7(a)～7(c)进行二值化求解得到空化面积占比分别为28.52%、32.26%和18.55%，空化面积占比随着液位高度的升高先增大后减小。因此，在固定超声功率下，合理的液位高度对空化面积有明显的增效作用。

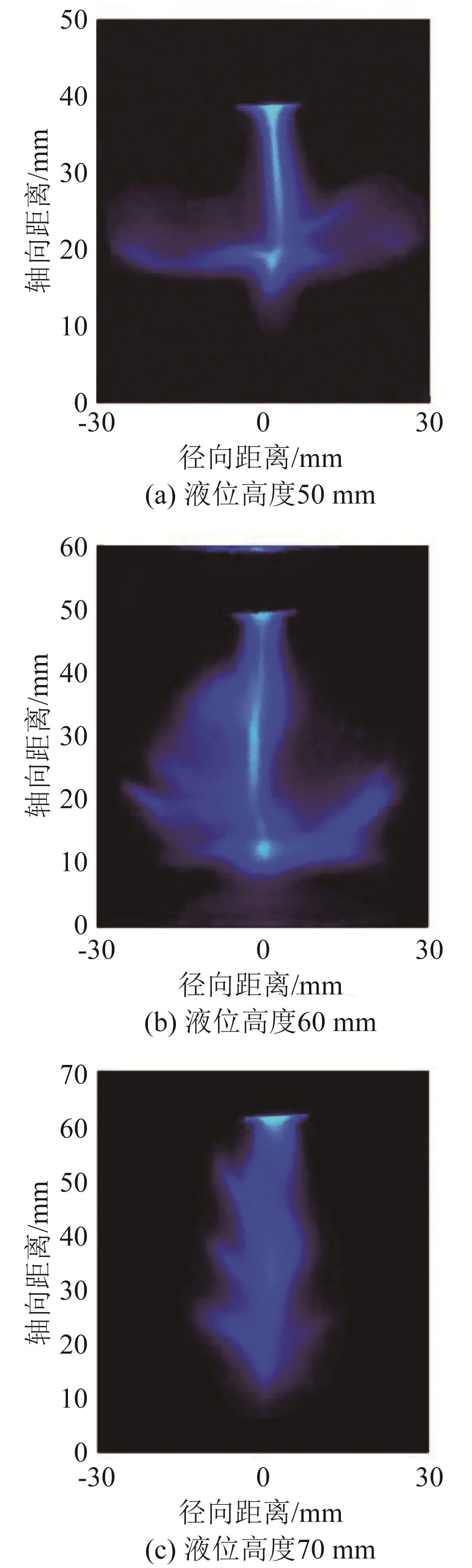
图7 不同液位高度下圆柱料腔内空化气泡分布的SCL图像Fig.7 SCL images of cavitation bubble distribution in the cylindrical material cavity under different liquid level heights

4 结果对比与分析

功放电流分别是40、80和120 mA时，内径为60 mm、液位高度为70 mm的圆柱料腔内声能密度分布如图8所示。声能密度表示了单位体积的液体中所具有的能量，由图8可知，料腔内高声能密度区域均分布于变幅杆端部附近，其他区域声能密度接近于零。根据能量守恒原理，空化气泡只能在高声能密度处形成，因此，在该形状尺寸下的料腔中，空化气泡只在变幅杆端部附近形成，且较大功放电流条件下变幅杆端部产生的气泡数量多。

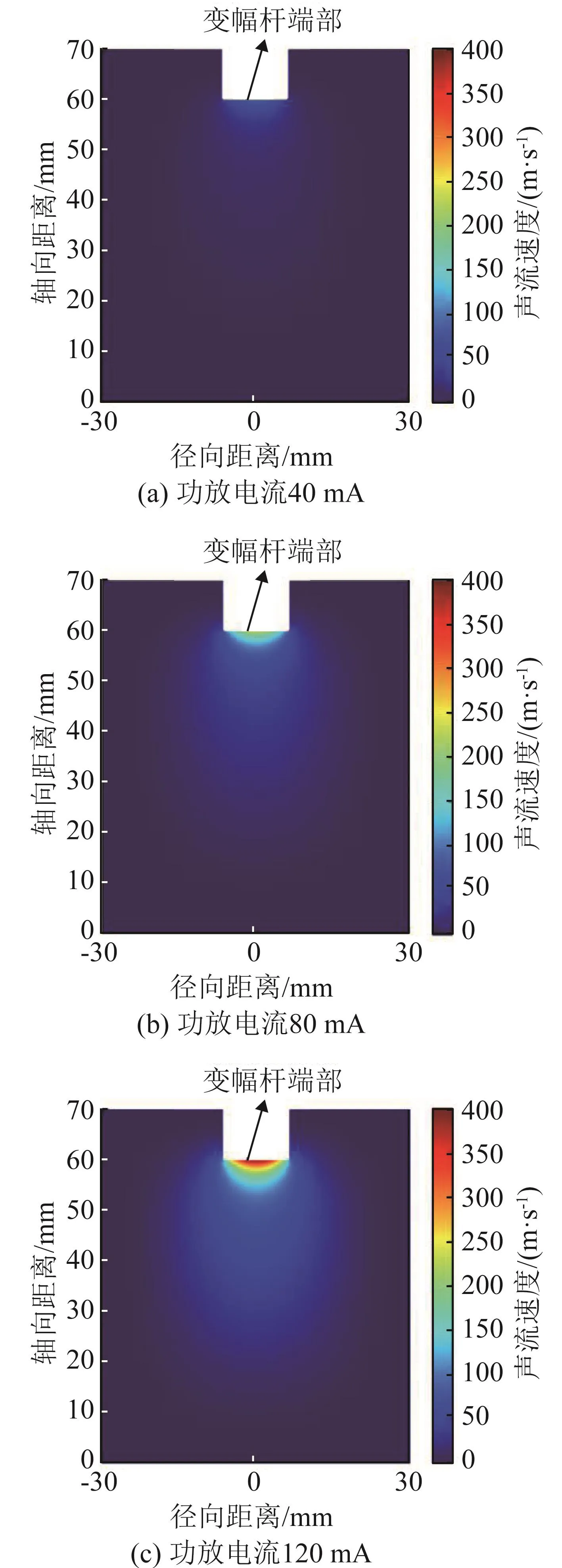
图8 不同功放电流下声能密度分布Fig.8 Distributions of sound energy density under different power amplifier currents

不同超声功率下声流速度分布与空化气泡分布对比如图9所示。图9表明不同超声功率时料腔内空化气泡的分布存在较大差异，原因是当功放电流为40 mA时，声流速度极值很小，认为声波是线性传播，无声流现象，空化气泡聚集在变幅杆端部附近，无法扩散；随着功放电流的增大，声波振幅增大，料腔内出现声流现象，空化气泡在声流作用下运动到距离变幅杆端部较远的区域，而不只存在于变幅杆端部的高声能密度区域。图9(b)和9(c)说明当声流现象出现后，圆柱料腔内超声空化气泡分布范围与声流速度分布区域吻合度较高，声流条件下空化气泡分布范围增大，空化面积增大，声化学反应效率增强。对比图9(a)～9(c)可知，空化气泡只在声流速度大于0.2、0.15和0.1 m·s-1左右的区域内分布，而在低于这些值的区域内几乎观察不到空化气泡的存在。因此，固定形状、尺寸的料腔声场达到一定的声流速度阈值时，才会出现空化效应区域增强效果，空化效应区域增强位于大于声流速度阈值的区域内。声流速度阈值由功放电流大小决定，当电流较小时，声流速度相应较小，气泡获得的动量就小，气泡还没运动到声流速度为0的区域就发生了溃灭；当电流较大时，声流速度相应较大，气泡快速扩散，气泡来不及溃灭就运动到了声流速度较小的区域，然后再发生溃灭。因此，功放电流越大，阈值越趋近于0，可近似得到声流条件下超声空化气泡理想的扩散和分布效果。

图9 不同功放电流下声流速度分布与空化气泡分布对比Fig.9 Comparison of acoustic flow velocity distribution and cavitation bubble distribution under different power amplifier currents

功放电流为80 mA，液位高度分别为50、60和70 mm时，内径为60 mm的圆柱料腔内的声流速度分布与空化气泡分布的对比如图10所示。图10(a)～10(c)表明，当功放电流相同、液位高度不同时，圆柱料腔内超声空化气泡的分布范围也存在较大差异。图10(a)表明液位较低时，声流速度较小，流场对空化气泡的曳力作用较弱，气泡获得的轴向动能较小，气泡还未溃灭轴向动能便已耗尽，气泡提前沿径向扩散。图10(b)表明液位高度增加时，声流速度增大，一部分空化气泡在声流的作用下从变幅杆端部区域沿轴向运动过程中径向扩散，一部分气泡运动到料腔底部时才发生偏转，最后扩散至料腔其他区域。图10(c)表明空化气泡只存在于变幅杆轴向区域，原因是虽然高液位时声流速度值较大，但是由于液位过高，空化气泡还未运动至料腔底部就已溃灭，且液位越高空化气泡运动的轴向距离越远。

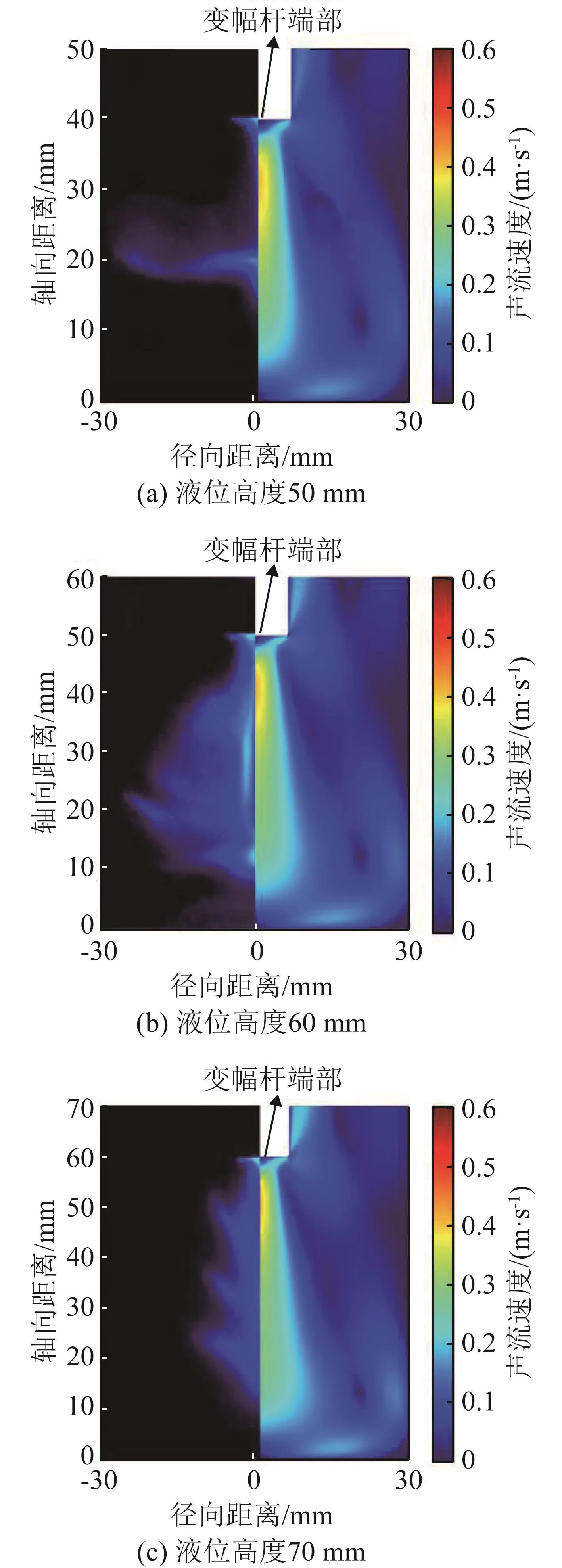
图10 不同液位高度时下声流速度分布与空化气泡分布对比Fig.10 Comparison of acoustic flow velocity distribution and cavitation bubble distribution under different liquid level heights

5 结论

本文基于有限元方法对内径为60 mm的圆柱形料腔中声流速度场的分布进行了仿真分析，并对声流条件下料腔中增大空化效应的规律进行探究；基于声致化学发光原理，采用20 kHz的超声对不同输入功率和不同液位高度条件下的圆柱料腔中超声空化气泡的分布进行了SCL图像测量。通过模拟仿真和实验测量，对圆柱形料腔内声流条件下空化气泡的分布进行了分析，得出了以下结论：

(1)在功放电流高于80 mA(电功率为17.6 W)时，在超声作用下，料腔声场中出现声流现象，流体介质获得动能从变幅杆端部出发，沿着轴向运动，在接触料腔底部时运动方向发生偏转，沿着料腔底部向壁面运动，最终形成稳定的往复运动的涡流。

(2)对比无声流现象和有声流现象两种情况，结果表明，在声流条件下，圆柱形料腔内空化气泡不再只聚集于变幅杆端部附近区域，而是在声流作用下沿变幅杆轴向运动扩散至其他区域，极大扩张了声化学反应的范围，提高了空化强度。

(3)声流条件下料腔内超声空化气泡的分布与功放电流和液位高度有关。液位高度相同时，当功放电流从40 mA(电功率为8.8 W)增加到120 mA(电功率为26.4 W)时空化面积占比提高了100.86%；功放电流(电功率)相同时，液位高度60 mm时空化面积占相对于50 mm和70 mm分别提高了13.11%和73.91%。空化气泡主要有在料腔中部沿径向扩散、沿变幅杆轴向且在料腔底部沿径向扩散、沿变幅杆轴向扩散三种扩散分布模式。

(4)在实际情况下，对于固定形状、尺寸的料腔，在声流条件下存在一个特定的声流速度阈值，当达到这一声流速度阈值时，才会出现空化效应区域增强效果，空化效应区域增强位于大于声流速度阈值的区域内。