钻柱偏心旋转对环空摩阻压降影响的数值模拟研究
田 野,蒋东雷,马传华,徐一龙,于晓东,宋洵成
(1.中海石油(中国)有限公司海南分公司,海南海口 570312;2.中国石油大学(华东)石油工程学院,山东青岛 266580)
斜井、大位移井和水平井等复杂结构井钻井过程中,钻柱在井眼中会出现偏心旋转,影响了环空钻井液的流动和循环压耗,进而使井底钻井液当量循环密度(ECD)发生变化,而准确预测环空摩阻压降是复杂结构井控压钻井的重要理论基础[1-2]。钻井液环空摩阻压降常规计算方法假设钻柱在井眼内居中,且未考虑钻柱旋转,因而无法直接计算复杂结构井的环空摩阻压降。为此,国内外学者开展了偏心环空摩阻压降计算理论和试验研究[3-25],建立了各种偏心环空流动摩阻压降计算模型,但均存在一定局限性,如解析模型中只考虑了偏心,没有考虑钻柱旋转,尚未建立符合现场工况的偏心环空摩阻压降计算模型。此外,环空层流摩阻压降的数值本身并不高,且偏心和旋转对环空摩阻压降的影响一般小于20%,因此,试验研究对压力计精度和操作精度的要求更加苛刻,导致文献公布的试验数据不系统,规律认识不一致。所以,基于试验数据建立的回归模型适用性差,现场应用时存在计算结果不合理现象。为此,笔者应用数值模拟方法,研究了正常钻井参数条件下,转速和偏心对复杂结构井典型环空(φ127.0 mm钻杆和φ215.9 mm井眼)摩阻压降的影响,进而建立了偏心旋转环空无因次摩阻压降计算模型,可以精细描述环空压力场和准确计算ECD,为控压钻井水力参数优化提供指导。
1 三维偏心环空流动数值模拟
1.1 数值模拟参数
复杂结构井的生产井段井径大多为215.9 mm,通常为控压钻井的主要井段。该井段钻进时,钻柱转速一般不超过120 r/min,钻井液排量不超过40 L/s。φ127.0 mm钻杆一般应用φ168.0 mm接头,考虑井眼10%的扩径率,钻杆接头紧贴井壁情况下的钻柱偏心度为62.89%,偏心度计算公式可表示为:
式中:E为偏心度;δ为偏心距,即沿井筒轴线视图中钻杆和井筒2个圆心间的距离,m;rw为井筒半径,m;rd为钻杆半径,m。
数值模拟时,假设钻井液性能和排量不变,改变钻柱转速和偏心度,主要模拟参数设定为:钻井液流性指数n为0.615,稠度系数K为0.518 Pa·sn,钻井液密度1 300 kg/m3、入口速度1.50 m/s,钻柱偏心度0~67.42%,转速0~114.65 r/min。由于偏心度和转速模拟矩阵划分得越细密,建立的回归模型预测结果精度越高,但模型也越复杂。综合考虑这2方面因素和偏心度对摩阻压降梯度的影响规律,不均匀设置了12个偏心度:0(偏心距0),22.47%(偏心距10 mm),26.97%(偏心距12 mm),31.46%(偏心距14 mm),35.96%(偏心距16 mm),40.45%(偏心距18 mm),44.94%(偏心距20 mm),49.44%(偏心距22 mm),53.93%(偏心距24 mm),58.43%(偏心距26 mm),62.92%(偏心距28 mm)和67.42%(偏心距30 mm);均匀设置了7个转速:0,19.11,38.22,57.32,76.43,95.54和114.65 r/min,构建了84个数值模拟点。
1.2 物理模型及网格划分
为消除入口段对模拟结果的影响,设定环空长度为5 m(大于20倍环空直径),重力方向为X轴,环空轴线方向为Z轴,应用Design Modeler建立了12个偏心度的环空流道几何模型,并进行了结构化网格划分以加速收敛。以22.47%偏心度模型为例,网格划分结果如图1所示,共划分了640 000个控制体网格,673 680个节点。网格最大扭曲度为0.28,最小扭曲度为1.54×10-2,平均扭曲度为0.13,网格质量优良,满足FLUENT对网格质量的要求,有利于计算收敛。
1.3 数值模拟方法有效性分析及参数设置
应用FLUENT进行三维偏心环空流动数值模拟分析时,需要确定的主要问题有:流态模型(层流或湍流模型)、离散格式、算法、非牛顿流体最大黏度及边界条件。笔者基于可以获取准确解析解的同心环空不旋转工况,确定上述参数。流速为1.50 m/s时,应用摩阻压降解析计算方法,得到雷诺数为2 300,层流摩阻压降计算结果(894.86 Pa/m)略大于紊流摩阻压降计算结果(853.00 Pa/m),故数值模拟研究时选择层流模型。为提高计算精度,选择二阶迎风格式,应用SIMPLE算法加速收敛。入口边界设定为速度入口(1.50 m/s),出口边界为压力出口,钻杆壁面和环空壁面为固体静止壁面,壁面处无滑移;在模拟钻柱旋转时,钻杆壁面处设定为对应的旋转角速度。调整钻井液黏度为最大值0.055 Pa·s时,数值模拟结果为896.91 Pa/m,与解析结果(894.86 Pa/m)相对误差为0.23%,故应用上述条件进行偏心旋转工况下的数值模拟分析。

图1 22.47%偏心度下偏心环空物理模型与网格划分Fig.1 Physical model and meshing of eccentric annulus with the eccentricity of 22.47%
2 数值模拟结果分析
2.1 偏心环空流动特征分析
以偏心度53.93%和转速114.65 r/min的情况为例,在模型轴线4 m处建立一个截面,该界面处轴向、切向速度剖面如图2、图3所示。为进一步分析偏心和旋转对流速的影响,在该截面处建立一条自窄间隙到宽间隙的高边方向线,获取并绘制偏心度53.93%、转速114.65 r/min,偏心度53.93%、转速19.11 r/min,偏心度22.47%、转速114.65 r/min和偏心度22.47%、转速19.11 r/min等4种工况下的轴向和切向流速沿该线的分布,结果见图4和图5。为方便分析,定义X轴正方向为井筒高边方向(自钻杆下方窄环空间隙指向钻杆上方的宽环空间隙),Y轴为截面中垂直于X轴的方向。

图2 偏心环空轴向流速剖面Fig.2 Axial velocity profile of eccentric annulus
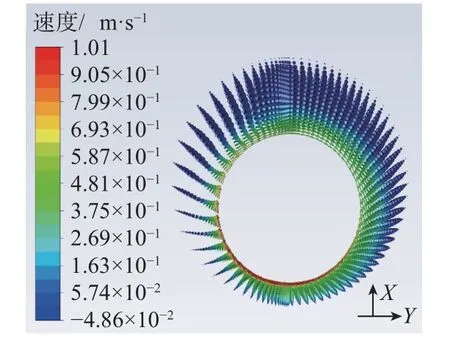
图3 偏心环空切向流速剖面Fig.3 Tangential velocity profile of eccentric annulus
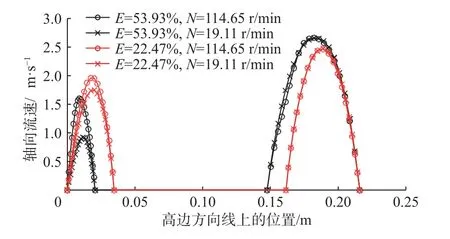
图4 轴向流速沿高边方向线分布Fig.4 Axial velocity distribution along the high-side direction line
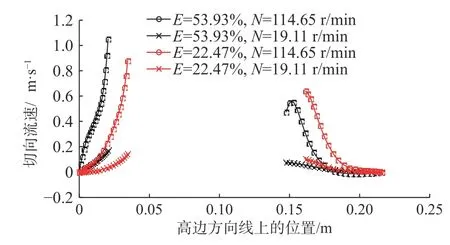
图5 切向流速沿高边方向线分布Fig.5 Tangential velocity distribution along the high-side direction line
从图2可以看出:1)钻杆上方环空中间区带的轴向流速最高,钻杆下方窄环空区带的轴向流速最低;2)钻杆顺时针旋转时,Y轴右侧环空的轴向流速高于左侧环空;3)钻杆壁面和井壁处的轴向流速为0,与数值模拟中2个壁面处的无滑移边界条件一致。
从图3可以看出:1)距离钻杆壁面越近,钻井液的切向流速越大;2)钻杆壁面下部区域的钻井液切向流速最大,上部宽环空区带的切向流速最小。
从图4可以看出:1)钻杆上方宽环空区带和钻杆下方窄环空区带的钻井液轴向流速均基本呈抛物线分布,壁面处轴线流速为0,中间位置轴向流速最大;2)偏心度越大,宽环空区带钻井液轴向流速越大,窄环空区带钻井液轴向流速越小;3)偏心度越大,转速对窄环空区带的钻井液轴向流速分布影响越大;4)相同偏心度条件下,不同转速下的宽环空区带钻井液轴向流速分布基本重合,即转速对宽环空区带的钻井液轴向流速影响极小。
从图5可以看出:1)窄环空区带的钻井液切向流速大于宽环空区带;2)偏心度越大,宽环空区带钻井液切向流速越低,窄环空区带钻井液切向流速越大,这2个区域钻井液切向流速差异也越大;3)转速比偏心度对钻井液切向流速的影响更大。
钻柱偏心和旋转对环空钻井液流速分布的影响复杂,难以直接得到二者对摩阻压降的影响规律。但从岩屑运移的角度来说,钻柱偏心度越大,转速对窄环空区带钻井液轴向流速和切向流速的影响越大,而钻杆下方恰恰是岩屑堆积的重点区域,因此可以推断,提高转速可显著改善大斜度井段岩屑的运移效果。
2.2 摩阻压降梯度数值模拟计算结果
流体在流道内的流动通常分为流动发展阶段和稳定阶段,为了准确获取摩阻压降梯度数值模拟结果,沿模型中钻柱上方流域中心点建立一条轴线,分析压力沿该轴线的变化情况,以确定数值模拟的流动稳定阶段。钻井液静压力沿轴线变化的模拟结果见图6。
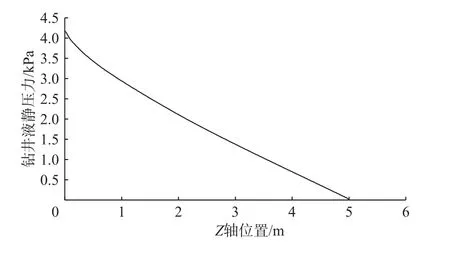
图6 钻井液静压力沿宽流域中心线的分布Fig.6 Static drilling fluid pressure distribution along the center line of wide flow domain
从图6可以看出,流道入口附近压降梯度较大,距流道入口1.50 m之后,钻井液静压力与Z轴位置呈理想线性关系,这表明流道入口1.50 m内为流动发展阶段,之后进入流动稳定阶段。基于此,在模型轴线2.00和5.00 m处建立2个截面,分析2个截面之间的压差,求取摩阻压降梯度。不同偏心度和钻杆转速下的摩阻压降梯度计算结果见表1。
2.3 偏心度对偏心环空摩阻压降梯度的影响
基于表1数据,绘制不同钻杆转速下环空摩阻压降梯度与偏心度的关系曲线,如图7所示(图中红色加粗直线为根据解析式计算出的同心不旋转摩阻压降梯度)。从图7可以看出:1)不同转速下,偏心度对环空摩阻压降梯度的影响规律不同,且没有单调关系;2)大多数情况下,偏心旋转环空摩阻压降梯度大于同心不旋转环空摩阻压降梯度,但在偏心度大于53.93%且转速小于38 r/min时,偏心旋转环空摩阻压降梯度低于同心不旋转环空摩阻压降梯度,也就是说,大斜度井段若采取滑动钻进方式且不考虑岩屑堆积造成的流动截面积减小,环空摩阻压降梯度会低于旋转钻进工况;3)不同转速下,偏心环空摩阻压降梯度与偏心度的关系曲线在偏心度约45%处存在一个交点,偏心度小于45%时,随偏心度增大,偏心环空摩阻压降梯度均略有增大;4)偏心度大于45%且转速高于57 r/min时,偏心环空摩阻压降梯度随偏心度增大而增大;5)偏心度大于45%且转速小于57 r/min时,偏心环空摩阻压降梯度随偏心度增大而减小。
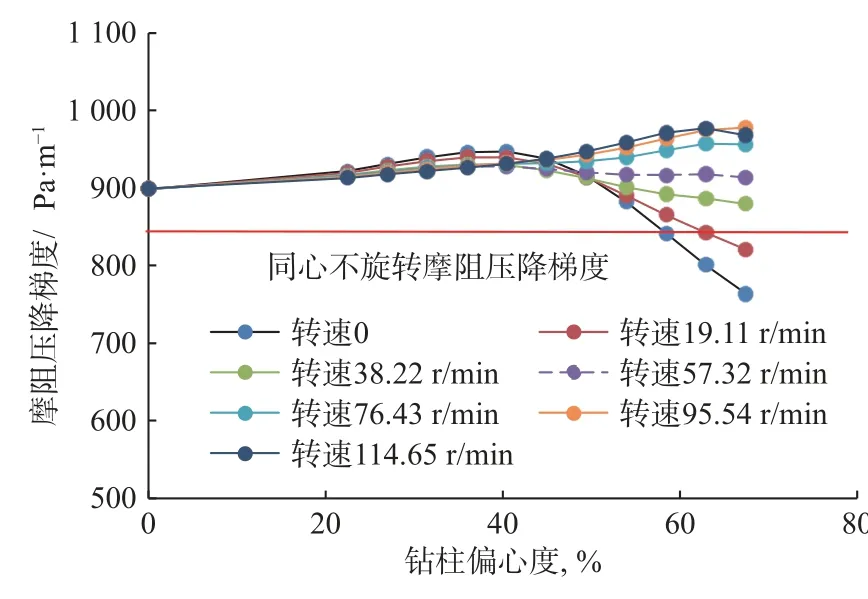
图7 偏心环空摩阻压降梯度与钻柱偏心度的关系曲线Fig.7 Variation of frictional pressure drop gradient in eccentric annulus with eccentricity of drill string
2.4 转速对偏心环空摩阻压降梯度的影响
基于表1数据,绘制不同钻杆偏心度下环空摩阻压降梯度与转速的关系曲线(见图8)。从图8可以看出:1)钻杆偏心度小于53.93%时,转速对环空摩阻压降梯度的影响较小,随着转速增大,偏心环空摩阻压降梯度略有降低;2)钻杆偏心度大于53.93%时,偏心环空摩阻压降梯度随转速增大而增大,但转速大于60 r/min后,转速对偏心环空摩阻压降梯度的影响减弱,也就是说,低转速下偏心度对摩阻压降梯度的影响远大于高转速情况。

表1 偏心环空摩阻压降梯度数值模拟计算结果Table 1 Numerical computation results of frictional pressure drop gradient in eccentric annulus

图8 偏心环空摩阻压降梯度与钻柱转速的关系曲线Fig.8 Variation frictional pressure drop gradient in eccentric annulus with rotational speed of drill string
3 偏心环空摩阻压降梯度预测模型的建立
将表1中的摩阻压降梯度数据除以同心不旋转工况下的摩阻压降梯度,得到无因次偏心环空摩阻压降梯度(见表2)。由于转速和偏心度对环空摩阻压降梯度的影响规律复杂,不具有单调特征,若强行建立一个综合考虑转速和偏心度的二元关系模型R=f(N,E),则预测精度会比较低。为此,按照偏心度和转速进行分类,分别建立偏心环空摩阻压降梯度预测模型。
建立心环空摩阻压降梯度预测模型时,定义了无因次旋转因子RN和无因次偏心因子RE:

式中:RN为无因次旋转因子,即相同偏心度下某转速时的摩阻压降梯度与基准摩阻压降梯度(即转速为0、偏心度为0时的摩阻压降梯度)的比值;RE为无因次偏心因子,即相同转速下某偏心度时的摩阻压降梯度与基准摩阻压降梯度的比值;Δpf,0为同心不旋转工况下的幂律流体摩阻压降梯度,Pa/m;Δpf,N为相同偏心度不同转速时的摩阻压降梯度,Pa/m;Δpf,E相同转速不同偏心度时的摩阻压降梯度,Pa/m。
将2类偏心环空摩阻压降梯度预测模型的预测结果与数值模拟结果进行比较发现,偏心度分类预测模型的残差平方和为3.61×10-4,而转速分类预测模型的残差平方和为2.25×10-3,前者的预测精度比后者高一个数量级,所以最终确定将表2中的数据进行回归,建立偏心度分类环空摩阻压降梯度预测模型。
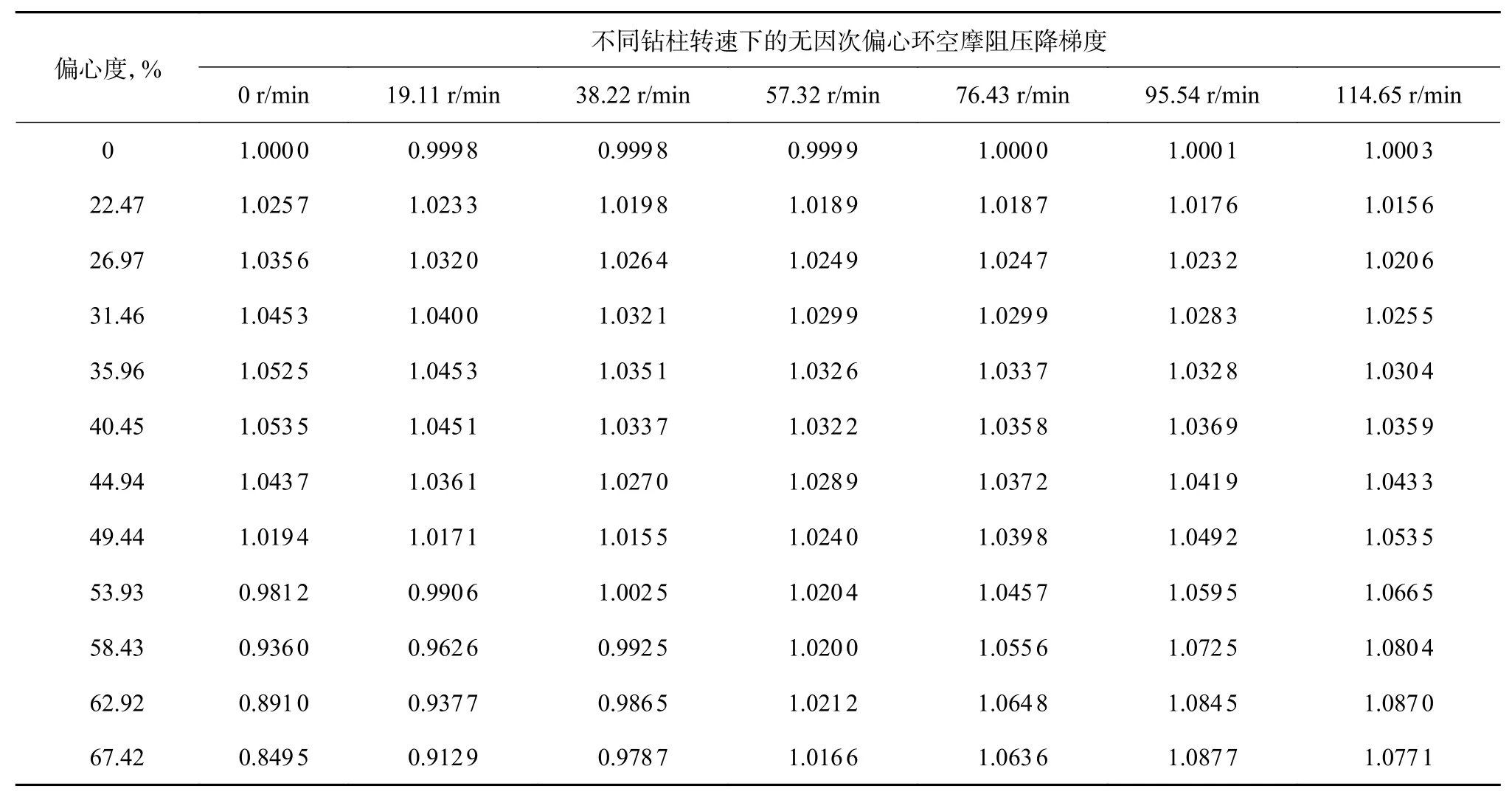
表2 无因次偏心环空摩阻压降梯度数值模拟结果Table 2 Numerical simulation results of dimensionless eccentric frictional pressure drop gradient
1)E=0时的预测模型为:
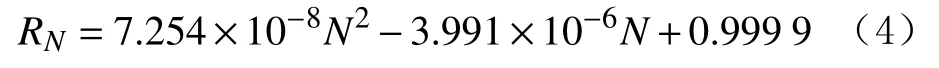
2)E=22.47%时的预测模型为:
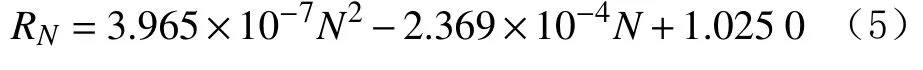
3)E=26.97%时的预测模型为:
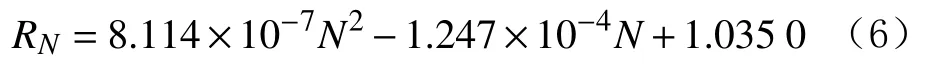
4)E=31.46%时的预测模型为:

5)E=35.96%时的预测模型为:
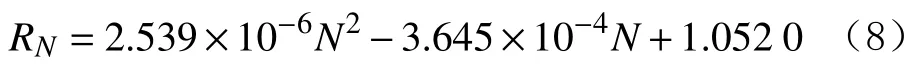
6)E=40.45%时的预测模型为:
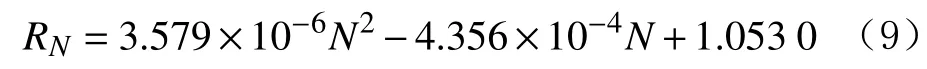
7)E=44.94%时的预测模型为:
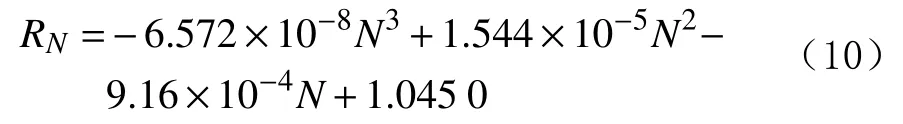
8)E=49.44%时的预测模型为:
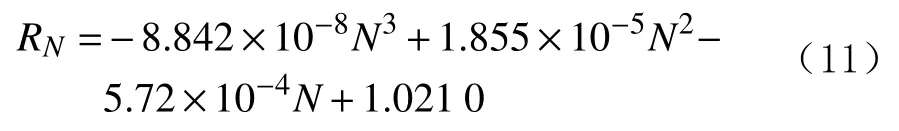
9)E=53.93%时的预测模型为:
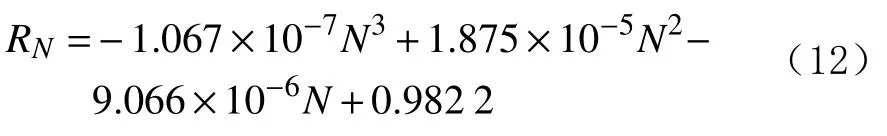
10)E=58.43%时的预测模型为:
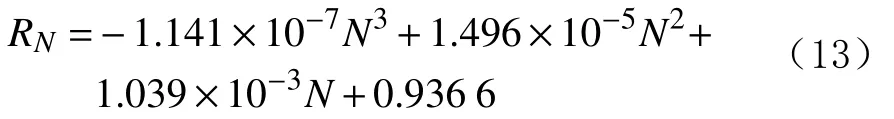
11)E=62.92%时的预测模型为:
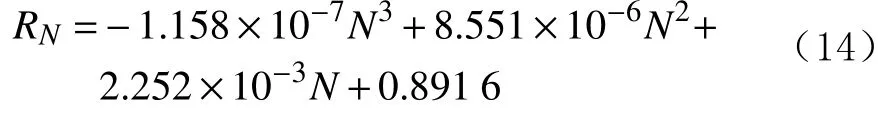
12)E=67.42%时的预测模型为:

式中:N为转速,r/min。
利用上述预测模型计算偏心环空摩阻压降梯度的主要步骤为:
1)基于钻井液流变性和流道尺寸,根据解析式[26]计算同心不旋转工况下的幂律流体摩阻压降梯度 Δpf,0;
2)根据计算点所在井段特征(增斜段、降斜段还是稳斜段),以及井斜角、造斜率、钻柱尺寸、井眼尺寸和稳定器尺寸等参数,依据钻柱屈曲理论[17,27-28],确定偏心度E;
3)查找偏心度E在12个偏心度的区间[E1,E2],选取相应的预测模型计算偏心度E1和E2时的无因次旋转因子RN,1和RN,2,应用插值法计算偏心度E时的无因次旋转因子RN;4)根据式(2)计算偏心环空摩阻压降梯度Δpf,N。
4 模型预测结果验证
南海某水平井水平段的钻具组合为:φ215.9 mm钻头+φ171.0 mm旋转导向工具+φ206.0 mm倒划眼稳定器+φ165.1 mm液压震击器+φ127.0 mm加重钻杆8根+φ127.0 mm钻杆。钻井液密度为1 280 kg/m3,稠度系数为0.72 Pa·sn,流性指数为0.66;钻井液排量为0.033 m3/s,钻柱转速为110 r/min。
基于上述数据,首先,应用Haciislamoglu方法[17]计算了偏心度为20%、30%、40%和50%时文中提出的无因次摩阻压降梯度系数Rlam(对应文中的RN),分别为0.94、0.98、0.98和0.98,均小于1.0,与现场工况不符,进一步印证了基于有限室内试验数据建立的回归模型的实用性不强。之后,应用建立的偏心环空摩阻压降梯度预测模型,以10 m为距离步长,计算了该井钻井液循环工况下φ215.9 mm井段偏心环空摩阻压降。为方便与现场PWD实测数据进行对比,按照已有公式计算得到了该井段的当量循环密度,计算值与实测值对比见图9,平均相对误差为0.45%,验证了模型的准确性。
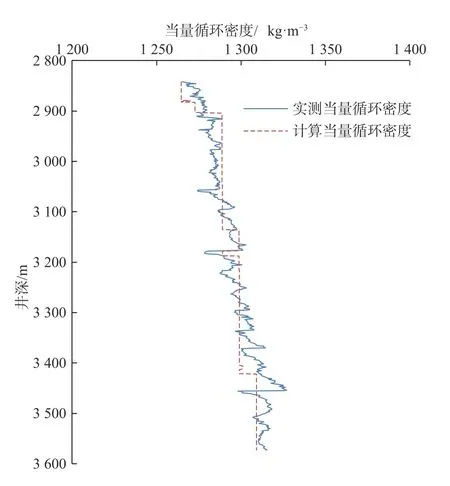
图9 南海某水平井φ215.9 mm井段当量循环密度计算值与实测值对比Fig.9 Comparison between calculated and measured values of ECD in φ215.9 mm section of a horizontal well in the South China Sea
钻井液循环工况下某井深处当量循环密度的计算公式为[29]:

其中
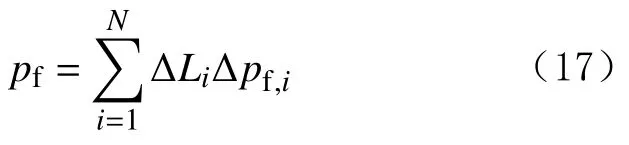
式中:ρce为当量循环密度,kg/m3;ph为静液柱压力,Pa;pf为摩阻压降,根据井眼轨迹分段计算并累计求和,Pa;Dv为目标点垂深,m。
5 结论与认识
1)三维环空流动数值模拟结果显示:偏心度越大,转速对窄环空区带的钻井液轴向流速分布影响越大,但转速对宽环空区带的钻井液轴向流速影响极小;窄环空区带的钻井液切向流速大于宽环空区带,偏心度越大,宽环空区带钻井液切向流速越低,窄环空区带的钻井液切向流速越大,这2个区域的钻井液切向流速差异也越大,转速比偏心度对钻井液切向流速的影响更大。
2)模拟计算结果显示,偏心环空摩阻压降梯度与偏心度、钻柱转速之间的关系复杂,不存在单调关系,难以建立综合考虑转速和偏心度的具有较高预测精度的二元关系模型;而按照偏心度和转速进行分类,分别建立偏心环空摩阻压降梯度预测模型,更有利于工程应用。
3)对比预测模型的预测结果与数值模拟结果发现,偏心度分类预测模型的预测精度比转速分类预测模型的预测精度高一个数量级,为此,通过对数值模拟数据回归分析,建立了偏心度分类环空摩阻压降梯度预测模型。
4)应用偏心度分类环空摩阻压降梯度预测模型,计算了南海某水平井的φ215.9 mm井段当量循环密度,并与PWD测试结果进行了对比,平均相对误差为0.45%,验证了模型的准确性,可用于精细描述钻井环空循环压力场和准确计算当量循环密度。

