基于异质能源统一建模方法的天然气网安全域稳态模型

宋晨辉，肖 峻，秋泽楷，焦 衡，屈玉清

（智能电网教育部重点实验室（天津大学），天津市 300072）

0 引言

综合能源系统（integrated energy system，IES）是实现多能互补与碳中和的关键载体［1］，中国能源局已将综合能源服务纳入发展规划［2］。但多能互联也带来了新的安全问题，即扰动易在异质能源系统传递，引发大范围连锁故障［3-4］。IES 安全性已成为国内外研究焦点。

IES 安全性研究主要基于“逐点法”［3，5-10］，包括稳态［3，5-7］与动态［8-9］两方面。针对稳态，文献［3］提出了多能流安全分析的概念；文献［5］提出一种灵敏度分析方法，可分析注入电功率对燃气压力的影响；文献［6］提出一种考虑管道N-1 的多能流安全分析方法；文献［7］研究了不同工况下耦合元件对IES 安全性的影响。文献［8-9］进一步考虑了动态，文献［8］建立了考虑动态的多能流模型；文献［9］进行IES 状态估计时，考虑了天然气暂态前后时间断面的相关性。

相较逐点法，电力系统安全域方法具有分析效率高、安全信息丰富的优势［10］，逐渐被应用于IES 及天然气网的稳态分析［11-16］。文献［11］提出了IES 安全域的概念，并提出一种高精度的边界拟合方法。文献［12］提出了基于凸包的IES 鲁棒安全域，并分析了忽略管存的稳态域的可用性。文献［13］在区域IES 安全域建模时考虑了N-1。对于天然气网，文献［14］提出了天然气网安全域的概念、模型与安全控制方法；文献［15］提出了天然气网在给定注入流量下的压力安全域。现有研究表明安全域对于天然气网的在线安全评估具有重要作用，能够判断供需关系下运行方案的可行性，为调度提供决策［14-15］。

但无论是逐点法，还是域方法，均以异质能源网各自固有模型为基础:如电力网采用潮流方程、天然气网采用管道压降方程［14］、热力网采用水力与热力方程［7］。这些模型的数学差异很大，缺乏统一框架，为异质能源的综合分析带来了壁垒［16-17］。

异质能源网本质上都是能量网络，可以从统一的视角进行建模分析［18］，文献［16-17，19-23］对此展开了研究。文献［19-20］最早将电路思想用于异质能源网分析，建立了多能源网络的广义电路理论［16，21］。文献［17，22-23］提出统一能路理论，建立了异质能源的能路模型，研究已涉及天然气网的气路［17］与状态估计［23］、潮流计算［22］等。

广义电路理论与统一能路理论的思想都是将异质能源系统的稳态与动态分析纳入统一框架，本文首次将该思想引入天然气网安全分析，提出了天然气网的安全域模型。较已有模型［14］，本文模型在数学形式上实现了天然气网和电力网在安全域上的统一，为后续建立IES 安全域通用化模型奠定了基础。同时，显著提升了天然气网安全域的计算效率，发掘了异质能源统一建模方法在天然气网安全分析中的应用价值。

1 天然气网安全域的基础概念

1.1 工作点

电力系统采用工作点［10］描述安全性。参考电力系统定义天然气管网工作点:能描述管网运行状态安全性的最小变量集合［14］。工作点选取运营商关心的流量作为变量［14］:

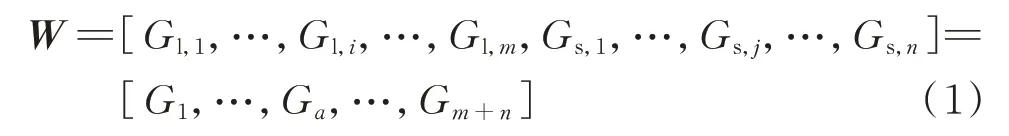
式中:W为工作点向量；Gl，i和Gs，j分别为负荷i、气源j的流量；m和n分别为负荷和气源的节点个数；Ga为节点a的流量，其中a=1，2，…，m+n。

1.2 安全性

天然气管网的运行安全性［14］定义为:对于某工作点，其所有状态量是否满足运行约束。若满足，则运行安全，该点是安全工作点，记为Ws；若不满足，则存在隐患，工作点不安全。

天然气管网的临界安全性［14］定义为:对于一个安全工作点，是否至少存在一个负荷节点，在其流量增加或减少后，形成的新工作点将不安全。若存在，则运行临界安全，原工作点是临界安全工作点，简称临界点，记为Wb。

临界安全性定义中，流量增加导致的临界安全性为正临界性，流量减少导致的临界安全性为负临界性。

1.3 安全域

天然气管网系统安全域［14］（security region for natural gas pipeline network system，NGS-SR）定义为:管网运行时，所有安全工作点构成的集合，记为ΩSR。NGS-SR 在状态空间中为封闭区域，域内点安全，域外点存在隐患。

安全边界［14］定义为:NGS-SR 中所有临界点构成的集合，记为∂SR。安全边界分为上边界和下边界:具有正临界性的全部临界点构成上边界；具有负临界性的全部临界点构成下边界。

输气能力（gas transmission capability，GTC）［14］定义为:天然气管网安全运行时的最大输气量。GTC 点是管网输气量最大时的运行状态，代表了NGS-SR 中最高效的工作点。

2 基于气路的天然气网安全域建模

2.1 稳态气路模型

异质能源统一建模时，基于气路建模天然气管网［17］，其气压与流量对应电路的电压与电流。本节在动态气路模型［17］基础上，建立稳态气路模型，包括管道稳态气路与网络稳态方程两部分。

2.1.1 管道的稳态气路

线性化天然气动量守恒方程，再推导得到管道稳态气路，如图1 所示，具体过程见附录A。

图1 天然气管道的稳态气路Fig.1 Steady gas circuit of natural gas pipeline

图1（a）为分布参数气路，用于刻画dx长度管道微元的气压降和流量差。图1（b）为图1（a）等效的π形集中参数气路［17］。

图1（a）中，Rg、Lg、kg、Cg、p分别为分布参数气阻、气感、受控气压源与气容、气压源气压。稳态时，“气感短路，气容断路”［17］，各元件公式如下:

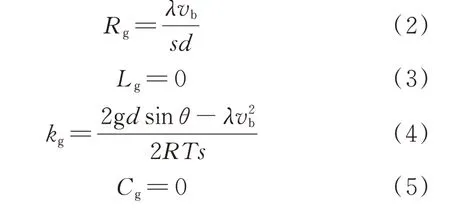
式中:λ、vb、s、d、θ分别为管道的摩擦系数、天然气流速基值、横截面积、内径和倾角；g 为重力加速度；R和T分别为天然气气体常数和温度。需注意:vb为气路建模的主要误差来源，其设定可根据经验或参考文献［22］。

稳态时，图1（b）中的集中参数计算公式如下:

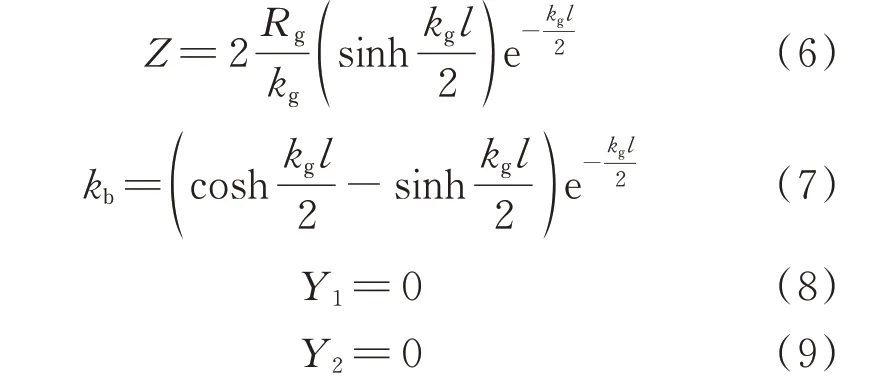
式中:Z、kb、Y1、Y2分别为π 形气路集中参数的支路阻抗、受控气压源和两端对地导纳；l为管长。

2.1.2 网络的稳态方程

在得到管道π 形集中参数气路后，进一步考虑管网支路特性［17］与网络拓扑，采用文献［17］方法可推导得到天然气网络稳态方程。文献［17］推导时将压缩机建模为气压源，对实际运行描述偏理想。在天然气领域，用压缩机压比模拟含压缩机管道的压力变化更为常见［23］，因此本文借鉴文献［21］，将压缩机建模为气路变压器:

式中:pc′、pc、K分别为压缩机首、末端气压和压比。

此外，本文规定节点流出为正方向。原因如下:管网分析时，若更关注负荷，通常规定流出为正［13-14］，而本文算例以负荷为主。

天然气网络稳态方程的具体推导过程见附录A，推导结果如下:

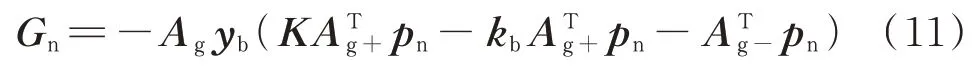
式中:Gn和pn分别为节点流量、气压构成的列向量；Ag、Ag+、Ag-分别为节点-支路关联矩阵、节点-流出支路关联矩阵和节点-流入支路关联矩阵，其含义见附录A；K为压缩机压比方阵，对于第i行、第i列元素(K)i，i，用(K)i，i=K表示支路i接入了压比为K的压缩机，否则取1；yb和kb分别为支路导纳和受控气压源构成的对角矩阵，矩阵元素采用π 形气路集中参数的稳态值。

引入广义节点导纳矩阵［17］Y'g:

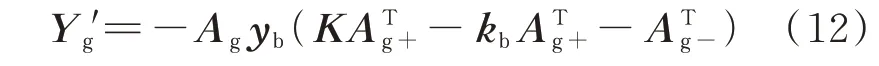
则天然气网络稳态方程将表示成与电力网络稳态方程相统一的数学形式:

需注意，上述气路模型中，天然气流量均采用质量流量；若采用体积流量，需在得到天然气质量流量结果后，除以标准状态下的天然气密度。

2.2 安全域模型

2.2.1 安全域

得到网络稳态方程后，可建模得到与电力网安全域数学形式相统一的天然气网安全域ΩSR。

式中:Gx、Gminn、pax、pin分别为节点流量和气压上、下限构成的列向量；A为Ag的左逆矩阵；Cb为管道容量构成的列向量；Kmax和Kmin分别为将矩阵K中的K替换为其上、下限值构成的矩阵；Ws为安全工作点，需满足平衡约束h(Ws)和安全约束g(Ws)，依次为:网络方程、节点流量和压力的上下限、管道流量上限、压缩机压比上下限。

上述安全域模型适用于输配气管网，原因如下:对于不同级别的管网，其模型都可采用本文的天然气网络方程，只是摩擦系数的计算公式不同，并不影响建模过程与结果。

2.2.2 安全边界

模型如式（15）所示，含义如下:Wb∈ΩSR表示工作点Wb位于域内，[Gl，1，…，Gl，i，…，Gl，j，…，Gl，m]是Wb中由负荷构成的向量。负荷i增加后形成新工作点W*，其中G*l，i为其元素。若∀ε*≠0，∃i=1，2，…，m，使得W*∉ΩSR，则Wb是一个边界点，全部Wb构成安全边界。若ε*＞0，则Wb具有正临界性，位于上边界；若ε*＜0，则Wb位于下边界。

2.2.3 输气能力

输气能力的模型如式（16）所示:

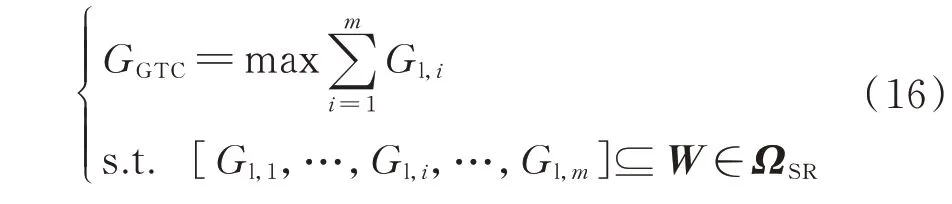
式中:GGTC为GTC 点流量；W∈ΩSR表示W是位于域中的安全工作点。

2.3 模型的统一性

附录B 表B1 对比了电力网安全域模型［10］、天然气网安全域传统模型［14］和本文模型。可以看出，本文模型在异质能源安全域建模中，体现出很好的统一性:传统模型的平衡约束采用管道压降方程，数学形式与电力网不同；而本文模型平衡约束采用网络方程，与电力网模型的数学形式一致。本文模型平衡约束能采用网络方程的原因是:在气路中，天然气流量与气压分别对应功率（电流）与电压，天然气网可表示为气阻等元件构成的气路图。网络方程只与气路图元件参数与拓扑相关，不受限于能量形式。

2.4 模型的保守性

本文的天然气网稳态安全域未考虑动态过程。天然气网传输较慢，其管存效应可缓解天然气生产与使用的不平衡［24］，使得域外点可能是安全的。虽然稳态域在判断安全性上具有一定保守性，但其在安全分析与调度中仍具备可用性。原因如下:

首先，电力系统存在类似先例。经典的基于稳定域边界的主导不稳定平衡点法［25］也具有保守性:通过该方法判断为稳定的情况，一定稳定；判断为不稳定的，再通过时域仿真判断。这将大大减少时域仿真次数，提高安全评估效率［25］。

其次，管网运行的实际流量通常小于设计流量，使得稳态域可满足多数情况下的安全分析与调度。

2.5 模型的扩展性

本文的天然气网稳态安全域，为扩展到动态安全域奠定了基础。后续可考虑如下路径:

路径1 是直接建立动态安全域模型，再研究求解方法。动态偏微分方程存在求解困难，可以在建模中，借鉴“统一能路理论”［17，22］和“广义电路分析理论”［16，21］将偏微分方程简化为代数方程。

路径2 是对稳态域结果进行修正。动态情况下，安全域是依赖于时间和分析节点的函数，但对于某时间断面的安全域，仍可采用本文提出的稳态建模方法。但稳态建模因未考虑管存而具有保守性，可采用动态仿真工具校验域外点的安全性，也可设计修正因子修正域。

在扩展到动态安全域时，还需考虑IES 的多时间尺度特性［26］。首先，电力系统也具有多时间尺度特性，可借鉴现有电力系统动态安全域的处理方法［10］。其次，还可借鉴广义电路理论和统一能路理论，将偏微分方程转化为代数方程，使得在分钟级与小时级的时间尺度内，能用统一模型来表征不同时间尺度能源网络的动态特性［16，22］。

本文模型能扩展适应IES 的多主体性［26］。当简化分析市场多主体机制时，安全域的统一分析可通过交换异质能源系统的边界信息，实现更高层面的多能源全局运行的安全和高效；当充分考虑市场多主体机制时，可通过对运行工作点和异质能源耦合关系进行约束，建立兼顾多主体利益的域模型。

3 安全域求解与观测

由于本文安全域模型不是显式的解析式，难以直接求解，故需进行仿真求解:先求解域的边界点，再对边界点拟合得到拟合表达式。求解到域后，还能进一步观测其二维/三维视图。上述方法的具体流程见附录C 图C1（a），包括3 步。

3.1 基于气路的安全域建模

1）输入管网参数:气体常数R，温度T，管道参数（摩擦系数λ等），节点流量与压力上下限Gmaxn、Gminn、pmaxn、pminn，压比上下限Kmax、Kmin。

2）将天然气管网等效为气路。

3）跟据式（2）至式（9）计算气路参数。

4）考虑管网支路特性和拓扑约束，根据式（11）至式（13）表示广义节点导纳矩阵和网络方程。

5）根据管网元件范围表示安全约束。

6）得到形如式（14）所示的安全域模型。

3.2 安全边界点计算

以上边界点为例说明，下边界点求解类似。

循环生成初始点W=[Gi，Gj]，对每个初始点迭代修正求边界点；修正时，修正Gi，保持Gj不变。对于M（M＞2）维安全域情况，同理选定一个负荷流量进行修正，其余M-1 个负荷流量保持不变。

1）参数初始化和生成首个初始点。设定初始点采样间距α，对Gj等间距采样。计数k=1，生成首个初始点，令Gi，1=Gmaxi或(Gmini+Gmaxi)/2，Gj，1=Gmaxj，其中Gmaxi和Gmini分别为节点i流量的上、下限。

2）由初始点求边界点。单个初始点求边界点子流程见附录C 图C1（b），这是一个基于二分法的修正过程，步骤如下。

步骤1:输入第k个初始点。

步骤2:设定修正步长初值β0、收敛精度ε、修正点安全性标志位Fs。ε是初始点迭代修正到边界点时修正步长需满足的精度，是迭代结束的一个条件。Fs是记录修正点是否安全的变量:若修正点安全，则Fs=1，否则Fs=-1。

步骤3:修正步长βi=β0，迭代次数ki=0；校验初始点安全性，根据安全性结果设置Fs初值。

步骤4:将初始点设为修正点迭代的初值。

步骤5:开始迭代，对修正点进行安全性校验。计算修正点的天然气流速基值vb。将修正点的负荷流量、气源压力、压缩机压比、天然气流速基值代入网络方程，计算修正点状态量。

若状态量满足安全约束，则为收敛性校验做准备，即ki=ki+1，Fs(ki)=1；若Fs(ki)Fs(ki-1)＜0，则令βi=βi/2，执行步骤6。

若状态量不满足安全约束，则该点位于域外，在边界上方，需对Gi进行负向修正，使该点向域内移动，即ki=ki+1，Fs(ki)=-1；若Fs(ki)Fs(ki-1)＜0，则令βi=βi/2，Gi，k(ki)=Gi，k(ki-1)-βi，生成下一个修正点，执行步骤7。

步骤6:收敛性校验。若βi≤ε，满足收敛性，则输出Gi，k、Gj，k，得到一个边界点，迭代结束；否则该点在域内，位于边界下方，需对Gi正向修正，使之向边界移动，即ki=ki+1，Gi，k(ki)=Gi，k(ki-1)-βi，生成下一个修正点，并令βi=βi/2，返回步骤4。

步骤7:若Gi，k(ki)=Gi，k(ki-1)-βi，初始点在Gi方向上无对应边界点，迭代结束；否则，返回步骤4。

3）若子流程2）修正到边界点，则记录该边界点Wb，k=[Gi，k，Gj，k]，生成下一个初始点:k=k+1，Gi，k=Gi，k-1，Gj，k=Gj，k+α，执行子流程4）；否则，已得到全部边界点，执行3.3 节步骤。

4）若Gj，k＞Gmaxj，则初始点在Gi方向上超出状态空间边界，已得到全部边界点，执行3.3 节步骤；否则返回子流程2）的步骤2，修正该初始点。

3.3 安全域的表达式拟合与观测

1）利用边界点对Gi、Gj分段线性拟合［11］，结合节点流量约束，得到安全域拟合表达式。

2）将求解结果绘于Gi-O-Gj平面，得到安全域视图。对于三维安全域，通过三维视图进行观测；对于M（M＞3）维安全域，利用文献［14］方法降维观测。

4 算例分析

4.1 算例原始数据

先采用5 节点天然气管网系统［14］作为测试算例进行验证。系统结构如图2 所示，其中N1～N5表示节点，C1表示压缩机，参数见附录D。

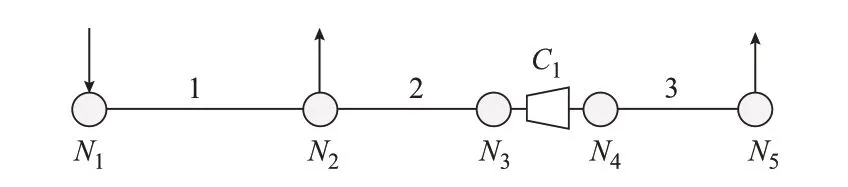
图2 5 节点天然气管网系统结构Fig.2 Structure of 5-bus natural gas network system

4.2 安全域建模求解

4.2.1 安全域建模

基于网络方程进行NGS-SR 建模，包括2 步。

1）将管网系统表示为如图3 所示的等值气路。系统将等效为3 段π 形等值气路串联形式。其中，Zbj、kbj、Ybj，1、Ybj，2（j=1，2，3）分别表示管道1、2、3 的支路阻抗、受控气压源和对地导纳。稳态分析时，气容和气感分别作断路和短路处理。

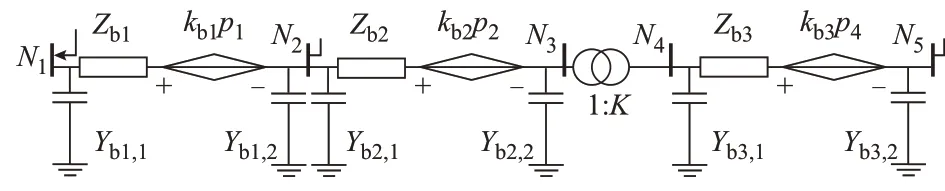
图3 5 节点天然气管网系统的等值气路Fig.3 Equivalent gas circuit of 5-bus natural gas network system

对应的形如式（13）所示的天然气网络方程如下:

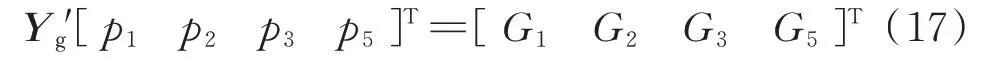
式中:G1、G2、G3、G5分别为节点N1、N2、N3、N5的流量；p1、p2、p3、p5分别为节点N1、N2、N3、N5的压力。Y'g的详细推导过程与表达式见附录E。

2）根据3.1 节，得到基于网络方程的NGS-SR模型如式（18）所示:

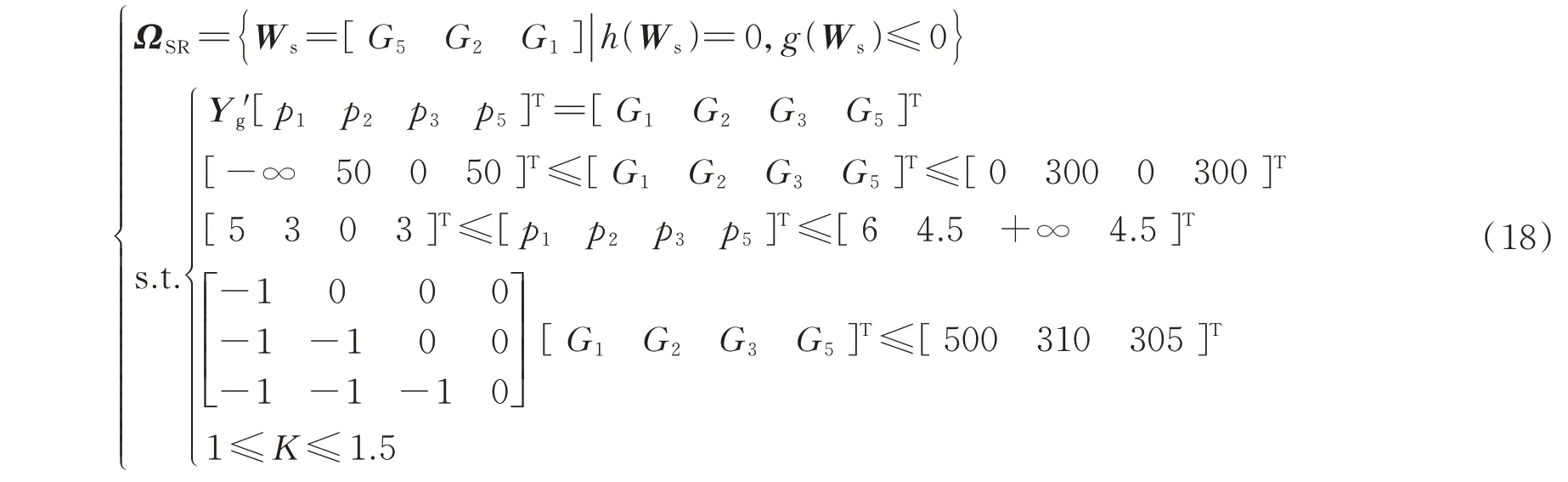
4.2.2 模型求解过程

首先，对工作点的安全校验过程进行说明。将待校验工作点对应的p1、G2、G3、G5、G3、G5、K与vb代入式（18），得到含4 个变量（G1、p2、p3、p5）的线性方程组，其系数矩阵与增广矩阵的秩相等，存在唯一解，可求得工作点全部状态量:若满足安全约束，则工作点安全；否则不安全。

然后，根据3.2 节，求解安全边界点:利用上述安全分析结果，修正初始点到边界点。图4 以上边界点为例对此过程进行展示。

以图4 中Wb，1=[80，297，-377]为例，示意了单个上边界点的迭代修正过程:

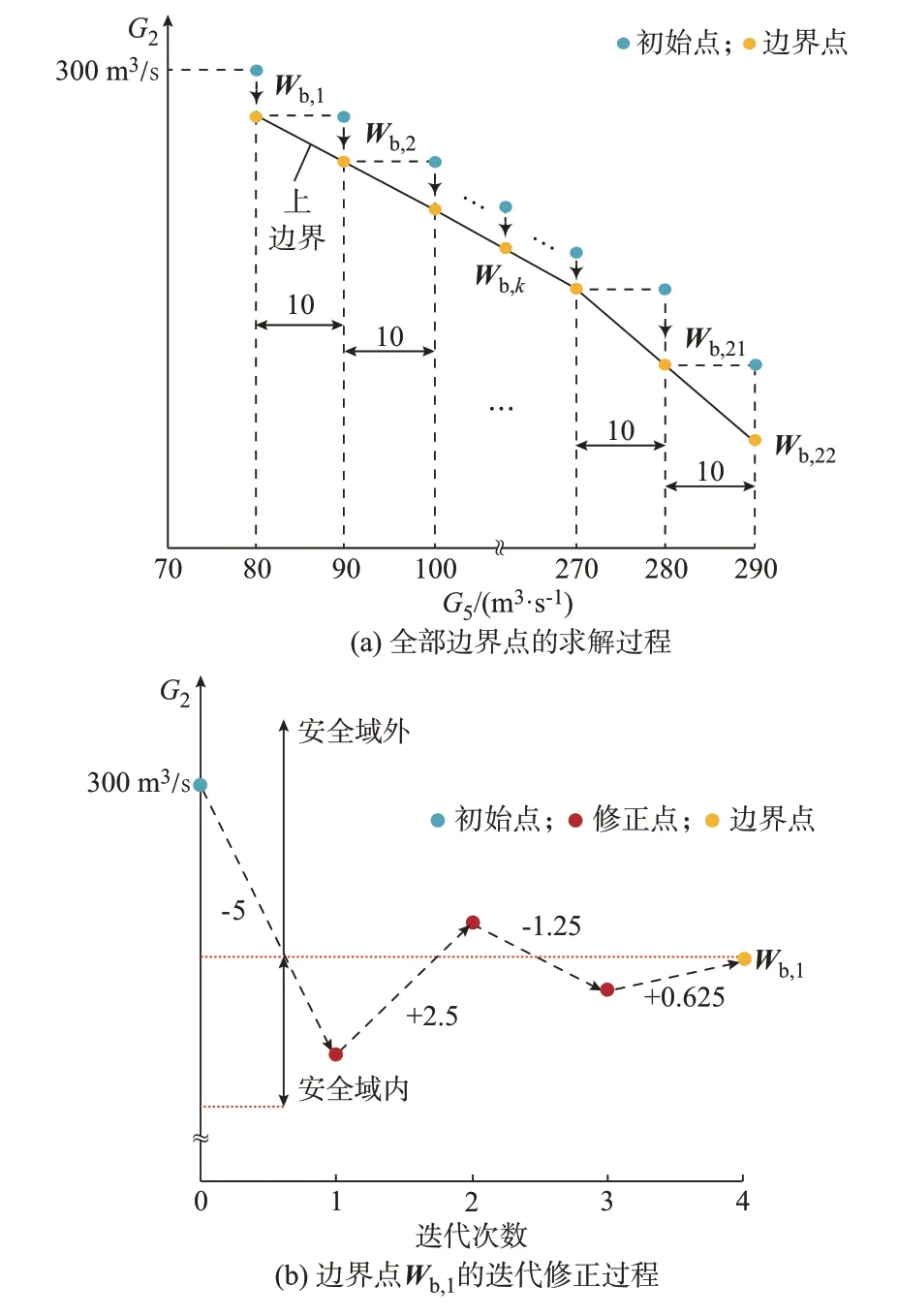
图4 上边界点求解过程Fig.4 Solution process of upper boundary points

1）初始点的G2取其上限值，即300 m3/s，修正步长β的初值取5 m3/s，收敛精度ε取1 m3/s；

2）校验修正点的安全性，根据校验结果对G2进行正/负向修正；

3）经过4 次迭代修正，修正步长依次为5，2.5，1.25，0.625 m3/s（+/-表示修正方向），修正点安全且β=0.625 m3/s＜1 m3/s，求解得到边界点Wb，1。

需说明，边界点求解平均迭代7 次，收敛很快。这是由于修正第k个初始点时，G2初值取第k-1 个边界点G2值，以保证其与边界点Wb，k很接近。附录F 表F1 展示了上边界点详细迭代次数。

最后，根据3.3 节，得到NGS-SR 求解结果，包括:1）上、下边界点；2）安全域拟合表达式。同时，还进一步给出了可视化图像。

4.2.3 求解结果

1）边界点

算例共求得上边界点22 个，下边界点7 个，详见附录F。上边界点包括15 个GTC 点和7 个输气量非GTC 的临界点（简称非GTC 点）。

2）NGS-SR 表达式与可视化图像

利用边界点对安全边界进行分段线性拟合，得到安全域的拟合表达式如表1 所示，包括4 段。

表1 5 节点天然气管网系统NGS-SR 的拟合表达式Table 1 Fitting expression of NGS-SR of 5-bus natural gas network system

本文拟合区域与精确域结果并无严格包含关系，但拟合结果偏保守，有助于保证区域内工作点的安全性。此外，利用文献［11］方法可计算得到拟合结果最大误差为0.41 m3/s，在0.1% 以内，精度较高。

图5 给出了NGS-SR 的观测结果，与表1 所示4 段表达式对应。

图5 5 节点天然气管网系统安全域Fig.5 NGS-SR of 5-bus natural gas network system

4.3 与传统方法对比

传统方法［14］基于管道压降方程对NGS-SR 建模，本文采用网络方程对NGS-SR 建模。本节对比2 种方法的求解结果和时间，以验证本文方法的正确性与高效性。首先对比状态量求解及安全分析，因为其是安全域计算的基础；然后对比安全域求解。本文的实验环境如下:2.50 GHz Intel Core i5-2450 处理器，内存4 GB，仿真平台MATLAB R2014a。

4.3.1 工作点状态量求解及安全分析的对比

针对某工作点，通过2 种方法计算其状态量，再进行安全性和临界性校验。以边界点Wb，1=[80，297，-377]、随机生成的安全工作点［58，155，-213］与不安全工作点［160，223，-383］为例对比，如表2 所示。表中，Gb1、Gb2、Gb3分别表示管道1～3的天然气流量。

由表2 可以得出以下结论。

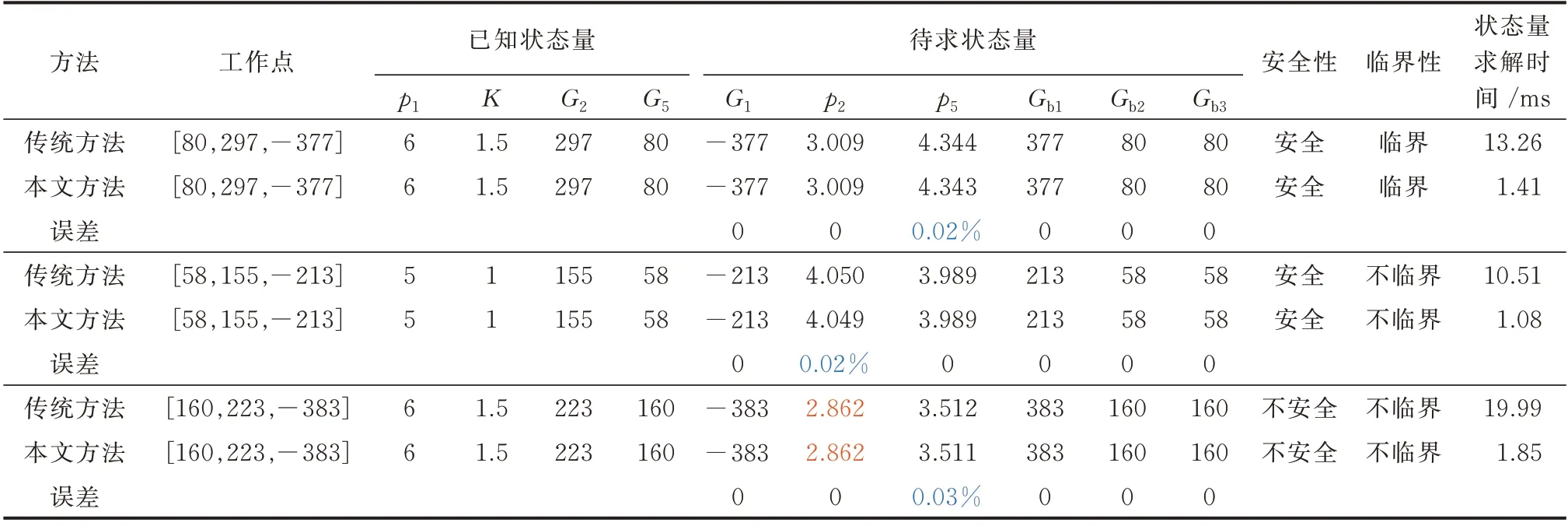
表2 典型工作点的状态变量计算结果、安全性与临界性校验结果对比Table 2 Result comparison of state variable calculation, security and criticality verification for typical operating points

1）本文计算的状态量有很小误差:仅气压存在误差，最大为0.03%。误差主要由于气路引入了天然气流速基值:若基值等于实际流速，则网络方程与管道压降方程等价，理论上将不存在误差；通过合理取值或修正基值可有效减小误差［22］。

2）由于状态量计算误差很小，不会影响到工作点安全性和临界性结果，具体验证见附录G。这为本文方法求解安全域边界点奠定了基础。

3）本文方法状态量计算效率提高约10 倍，原因是建模时线性化了天然气流动过程的动量守恒方程［17］，避免了传统方法采用非线性管道压降方程求解时的迭代过程。

4.3.2 安全域求解的对比

首先，对比建模结果。传统方法［14］结果如式（19）所示。相较本文模型式（18），式（19）含管道压降方程这一非线性约束（约束第一式），更为复杂。

其次，对比模型求解结果。以N2、N5为观测节点，以10 m3/s 为采样间隔，采用传统方法［14］求解边界点，与本文结果对比，如表3 所示。

由表3 看出，2 种方法求解的边界点相同，故由此得到的拟合表达式及NGS-SR 图像也一致，说明了本文方法的正确性。求得边界点相同的原因如下:网络方程引入的状态量求解误差很小，未影响到工作点的安全性与临界性校验结果。

表3 传统方法和本文方法求得的边界点对比Table 3 Comparison of boundary points obtained by traditional method and proposed method

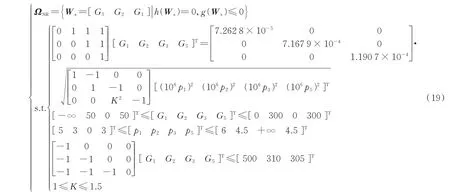
最后，比较NGS-SR 求解时间。对于测试算例，传统方法耗时582.58 s，本文方法仅耗时22.07 s，求解效率提高26.40 倍。原因是:1）本文基于网络方程的模型求解不存在非线性方程求解的迭代过程；2）引入二分法，提升了边界点的修正效率。

此外，本文NGS-SR 计算效率的提升是由模型改进带来的，而非由算法改进带来的。换而言之，其他算法可与本文模型结合，进一步提升计算效率。

4.4 实际算例验证

4.4.1 算例原始数据

以图6 的比利时东南地区管网［14］为例进行验证，包含9 个节点N1～N9、11 条管道与3 台压缩机C1～C3，参数见附录H。

图6 比利时东南地区天然气管网系统结构Fig.6 Structure of southeastern Belgium gas network system

4.4.2 安全域结果

首先，边界点求解参数如下:以5 m3/s 为采样间隔，对节点N3、N5、N8的负荷在状态空间中采样；修正节点N9负荷。对于首个初始点，N9节点处负荷初值取30 m3/s；修正步长初值取4 m3/s，其收敛精度取1 m3/s。

上述参数条件下，共求解到上边界点338 个，包括155 个GTC 点和183 个非GTC 点，详见附录I。下边界仅为一个点，即［0，0，125，69，-194］，该点是状态空间边界下限的交点。

接着，利用边界点进行拟合，结果如表4 所示。

表4 比利时东南地区天然气管网系统的NGS-SR 拟合表达式Table 4 Fitting expression of NGS-SR of southeastern Belgium gas network system

最后，由于本算例安全域维度大于3，可通过降维观测可视化，附录J 进行了展示。

4.4.3 与传统方法对比

关于求解结果，传统方法［14］求得的边界点与本文相同，进而拟合表达式也与表4 相同。本文方法与传统方法的差异仅在求解过程:由于引入流速基值，工作点的状态量计算存在微小误差。但该误差并未影响到工作点的安全性和临界性校验结果。

关于求解时间，传统方法耗时164.06 h，本文耗时3.23 h，效率提高约50.79 倍。可见，随着算例规模增加，本文方法的计算效率优势更加明显。

5 结语

本文借鉴异质能源统一建模的思想，对天然气网安全域的建模与求解进行了研究主要贡献如下:

1）提出了基于异质能源统一建模方法的天然气网安全域稳态模型，在安全分析上实现了天然气网和电力网的数学形式统一；

2）提出了天然气网安全域的全维求解方法，能得到域边界点与拟合表达式，并实现可视化观测；

3）通过经典5 节点算例和比利时管网实际算例验证了本文模型及方法的正确性；本文方法效率相对现有方法提升了1 个以上数量级。

本文工作表明了异质能源统一建模方法在天然气网安全分析中的应用前景，为电、气、热异质能源的综合安全分析奠定了基础。本文方法可扩展到天然气网动态安全域，扩展后将更具备实际价值。下一步研究主要包括考虑动态特性和多主体特性的IES 安全域、IES 安全域的解析表达式等。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。