多区域互联电-气耦合系统分散协调分布鲁棒优化调度

张亚超，谢仕炜，朱 蜀

（1. 福州大学电气工程与自动化学院，福建省福州市 350108；2. 国网湖南省电力有限公司调度控制中心，湖南省长沙市 410004）

0 引言

近年来，为提高风电、光伏等可再生能源的消纳水平，建设多能互补融合的综合能源系统已成为能源互联网发展的重要方向［1］。基于电力与天然气系统的物理互联和交互作用开展电-气耦合系统协同优化研究具有重要意义［2-3］。

针对含可再生能源的电-气耦合系统的协同优化运行，文献［4］引入区间数表征风电出力的不确定性，以电力、天然气网联合运行成本的区间函数为目标构造多目标优化问题，求解得到区间形式的调度决策。文献［5-6］建立基于风电出力场景集的两阶段随机规划调度模型，然而场景集规模对模型求解效率和决策有效性有直接影响。文献［7］构造风电出力不确定量的盒式不确定集，并采用鲁棒优化（robust optimization，RO）方法寻求最恶劣场景下的调度决策。鉴于传统RO 所得决策过于保守的缺点，文献［8-9］分别建立风电出力不确定量的模糊集和概率分布置信集，提出分布鲁棒优化（distributionally robust optimization，DRO）调度模型求解电-气耦合系统的协调优化决策。

然而，上述研究均假设电力、天然气系统的运行参数和状态信息同步共享，在集中优化框架下制定综合能源系统的协同调度决策。在工程实际中，电力、天然气系统分属不同能源供应商，仅支持少量数据信息的交互。因此，研究电-气耦合系统的分散式优化方法具有实际应用价值。文献［10-11］针对电力、天然气系统的多主体自治决策特点，提出了基于交替方向乘子法（alternative direction method of multipliers，ADMM）的电-气耦合系统的分散式协同优化框架，但未计及风电出力不确定性的影响。文献［12］建立了面向风电消纳的日前-实时两阶段嵌套分散协调鲁棒调度模型，并采用改进的ADMM和列与约束生成（column and constraint generation，C&CG）方法进行求解。

现代综合能源系统可看作根据地理区域划分的几个子系统构成的一个大规模能量耦合系统。不同子系统的能量交互可提高系统运行的灵活性和可靠性，促进可再生能源消纳［13］。针对可再生能源出力的不确定性，文献［14］和文献［15］分别提出基于分区可调RO 和DRO 的多区域电力系统分散式协同调度模型。文献［16-17］针对多区域互联的电-气耦合系统建立了基于ADMM 求解的分散式协同优化框架。文献［18］提出了计及风电不确定性的多区域电-气耦合系统分散协调鲁棒调度模型。上述研究中存在如下问题亟待解决:未充分考虑多区域互联系统中风电出力、燃气机组耗气量及联络线交互能流等不确定因素的影响，使得协同调度计划的有效性受到质疑。其次，如何在风电出力不确定集中融入更多的不确定量统计信息，以提高系统运行的经济性。此外，尽管ADMM 已广泛应用于多区域分散协调优化问题，但当子问题数较多时无法保证算法的内在公平性，且求解效率较低。

综上分析，本文提出一种计及风电出力、燃气机组耗气量及联络线能流交互不确定性的多区域互联电-气耦合系统多决策主体分散式协调优化框架。针对各区域内配电网，建立基于风电出力模糊集的DRO 调度模型以降低传统RO 决策的保守性，并通过优化区域间联络线交互功率基值及调整量实现区域间的备用共享，提高系统运行的经济性和灵活性。针对各区域天然气网，建立二阶锥规划模型，根据燃气机组耗气量范围检验其备用配置的有效性。此外，在构建各决策主体协同交互机制的基础上，采用一种基于平行正则化改进的ADMM 求解上述分散式协调优化调度模型，减轻区域间信息交互量，提高求解效率，并实现多区域系统的全局优化。最后，以3 区域互联电-气耦合系统为例，验证了所提模型和求解方法的有效性和实用性。

1 多区域电-气耦合系统结构

本文构建的多区域互联电-气耦合系统的基本结构如图1 所示。

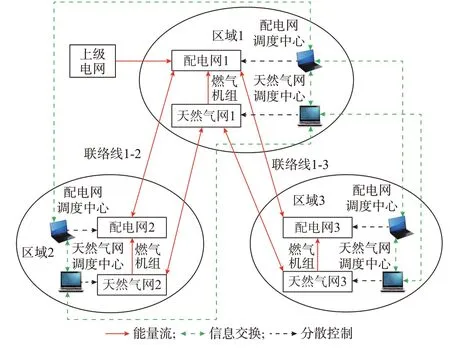
图1 多区域电-气耦合系统Fig.1 Multi-area electricity-gas coupling system

该系统包括3 个不同区域的综合能源系统，各区域内的配电网和天然气网以燃气机组作为耦合元件。区域1 内配电网与上级电网相连，并通过联络线1-2 和1-3 分别同区域2 和3 内的配电网连接。区域1 内天然气网通过联络管道1-2 和1-3 分别同区域2 和3 内的天然气网相连。同一区域内的配电网和天然气网，不同区域的配电网、天然气网之间根据其耦合元件和联络元件的运行约束条件分别构建耦合变量实现信息交换，各配电网和天然气网决策主体在“分散控制、协同优化”的框架下通过自治优化来实现多区域互联电-气耦合系统的最优协调调度。

2 电-气耦合系统模型

2.1 天然气网模型

天然气网中气井产出的天然气通过管道输送至气负荷节点。天然气网的购气成本为:

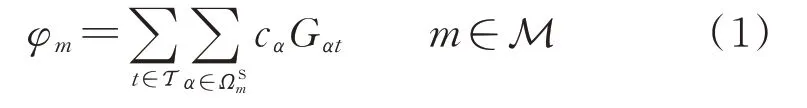
式中:φm为区域中天然气网在整个调度周期内的购气成本；cα为气源α的供气价格；Gαt为气源α在时段t的供气流量；m和M分别为区域的索引和集合；t和T分别为调度时段的索引和集合；ΩSm为区域m中的气源集合。

天然气网运行约束包括气源流量约束式（2）、节点气压约束式（3）、管道气潮流方程式（4）和式（5）、管道流量约束式（6）和流量平衡方程式（7）。

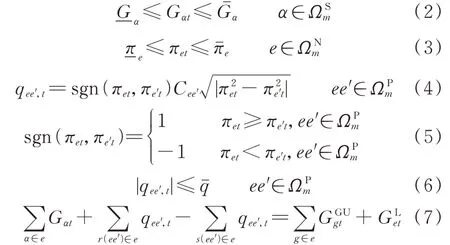
2.2 配电网分布鲁棒调度模型

面向多区域互联的配电网，本文提出一种考虑风电出力、燃气机组耗气量以及联络线传输有功功率等多重不确定性的分布鲁棒调度模型。区域m中配电网目标函数fm包括日前和实时阶段的系统运行成本，可表示为:

式中:F0(·)和Ft(·)分别表示日前阶段和实时阶段的目标函数；为日前阶段决策变量；EPt(·)为求期望；ξ͂t为时段t风电预测误差不确定量构成的向量；Pt为ξ͂t在模糊集Ft上的分布。

2.2.1 日前阶段建模

配电网在日前阶段的决策变量如下:

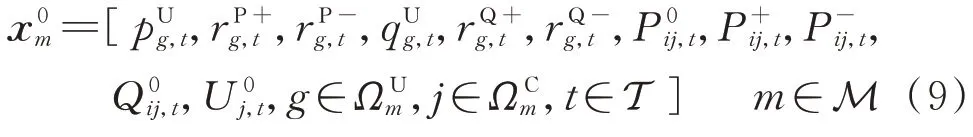
式中:p和q分别为机组g在时段t发出的有功和无功功率；r和r分别为机组g在时段t提供的向上、向下有功备用容量；r和r分别为机组g在时段t提供的向上、向下无功备用容量；P和Qt分别为配电网子系统经联络线ij流入耦合节点j的有功和无功潮流；P和P分别为联络线ij中有功潮流的向上、向下调节容量；U为耦合节点j在区域m内配电网侧的节点电压；ΩUm和ΩCm分别为配电网中发电机组和耦合节点的集合。

日前阶段的目标函数包括机组发电成本、有功/无功备用容量成本以及联络线有功调节容量成本，可表示为:

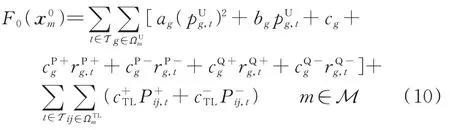
本文采用不考虑网损的线性化潮流模型［19］，日前阶段的运行约束条件如下:

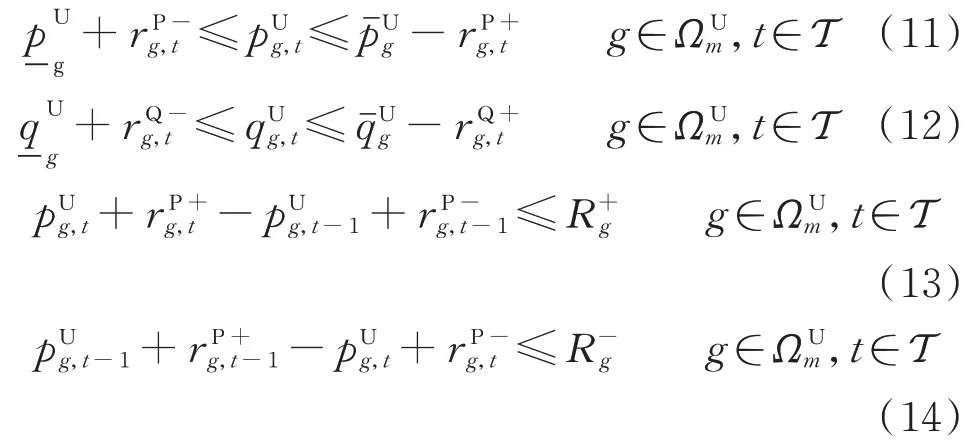
2.2.2 实时阶段建模

配电网实时阶段的决策变量xtm可表示为:

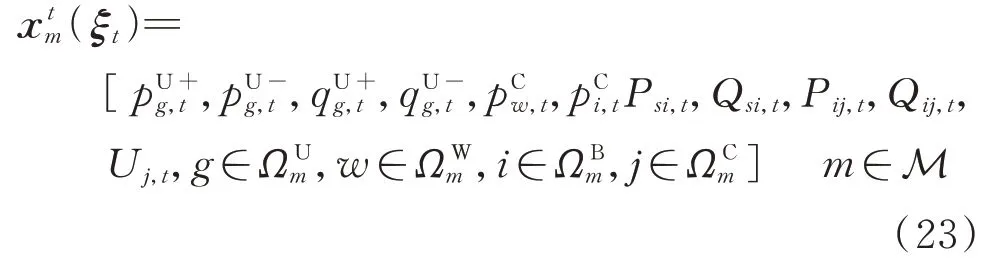
式中:ξt为不确定量ξ͂t的某一具体值；p和p分别为机组g在时段t的向上、向下有功出力调整量；q和q分别为机组g在时段t的向上、向下无功出力调整量；p为风机w在时段t的弃风量；p为配电网节点i在时段t的弃负荷量；Psi，t和Qsi，t分别为上级电网节点s注入配电网节点i的有功和无功功率；Pij，t和Qij，t分别为配电网子系统实时阶段经联络线ij流入耦合节点j的有功和无功潮流；Uj，t为配电网实时阶段节点j的电压值；ΩWm为区域m内风机集合。

针对不确定量ξ͂t的某一具体值ξt，与上级电网相连的配电网子系统在实时阶段的时段t的目标函数包括购电成本，弃风、弃负荷成本以及机组的有功、无功调整成本，可表示为:

式中:i∈π(s)表示与上级电网s相连的配电网节点i；cM为主网购电价格；cW和cL分别为单位弃风、弃负荷的惩罚价格；dP+g和dP-g分别为机组g的向上、向下有功调整价格；dQ+g和dQ-g分别为机组g的向上、向下无功调整价格。

在某一时段t，配电网的运行约束条件如下:

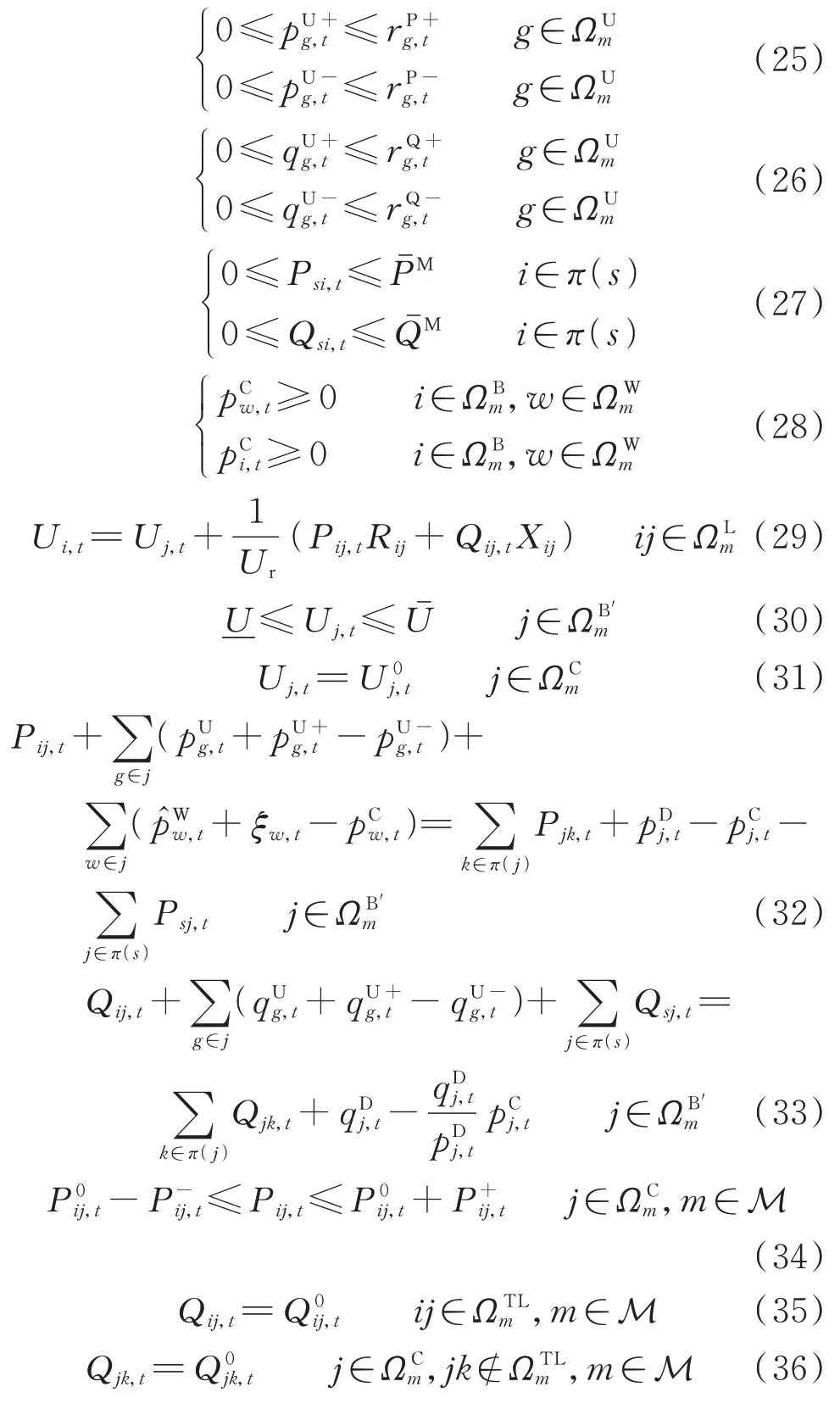
2.3 同一区域内电-气耦合关系

配电网和天然气网之间的耦合变量为燃气机组出力，为与配电网侧区分，将天然气网侧燃气机组出力及向上、向下备用容量分别表示为p，r和r。同一区域内配电网和天然气网的一致性约束为:

式中:ΩGUm为区域m内的燃气机组集合。

机组出力与耗气量的关系如下:

式中:FHHV为天然气高位热值；Gg(·)表示机组g的耗气量函数；αg和βg为机组g的耗气量参数。

由于配电网中燃气机组提供备用容量配置的有效性受到天然气网可供气量的影响，即燃气机组提供向上、向下备用容量的极端场景分别对应机组耗气量的最大、最小需求，故燃气机组耗气需求不确定性集的边界值可表示为［20］:

2.4 多区域互联网络的一致性约束

如图2 所示，以区域m和区域n内配电网为例，图中互联节点i和j之间线路为联络线，对网络进行解耦后将联络线ij归入区域m内配电网，将节点j视为两个网络的耦合节点，其一致性约束可表示为:

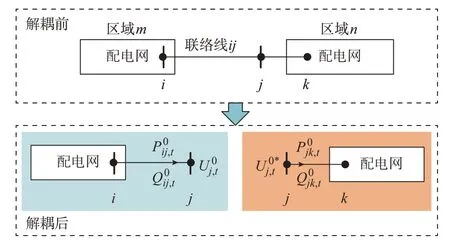
图2 多区域互联配电网的一致性约束Fig.2 Consistency constraints of multi-area interconnected distribution networks

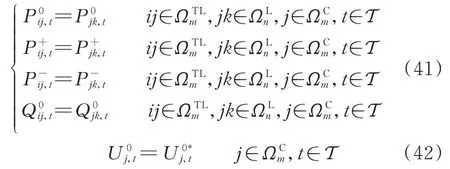
式中:U为耦合节点j在区域n内配电网侧的节点电压。

同理，设区域m内天然气网节点i′和区域n内天然气网节点j′通过管道i′j′联络，可对其解耦后将联络管道i′j′归入区域m内天然气网，将节点j′视为两个天然气网的耦合节点，其一致性约束可表示为:

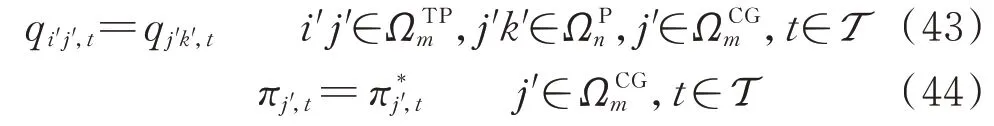
式中:ΩTPm和ΩCGm分别为区域m内联络管道集合和天然气网耦合节点集合；πj′，t和分别表示耦合节点j′在区域m内和区域n内天然气网侧节点的气压。

3 模型求解

计及风电不确定性的配电网，结合对偶理论和线性决策规则对上述DRO 问题求解，针对天然气网的非线性优化问题，结合二阶锥松弛技术转换为二阶锥模型求解。在此基础上，提出一种改进的ADMM 求解多区域互联系统的分散协调调度问题。

3.1 配电网子问题求解

配电网的DRO 问题可表示为如下紧凑形式:

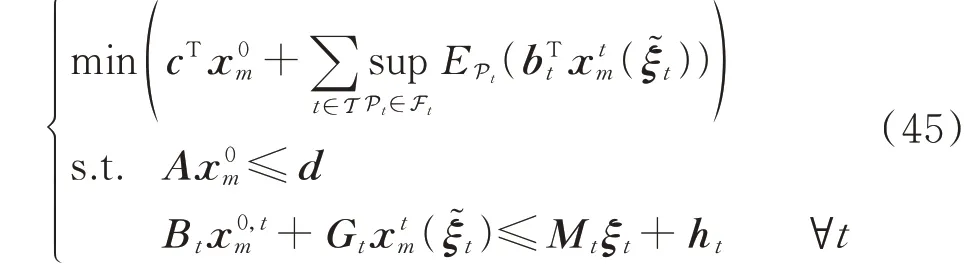
式中:c、d、bt、ht为常系数向量；A、Bt、Gt、Mt为常系数矩阵；x为在日前阶段的时段t 的决策变量构成的向量。

模糊集Ft可表示为:

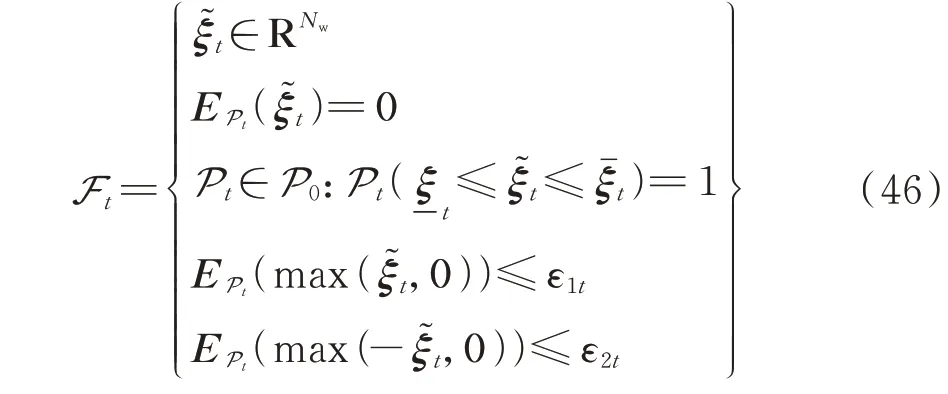
式中:P0为不确定量的概率分布集合；Nw为风机数目；E Pt(·)表示求Pt分布下的期望；和分别为风电预测误差的上、下边界；ε1t和ε2t为风电预测误差矩信息的分布特性参数。

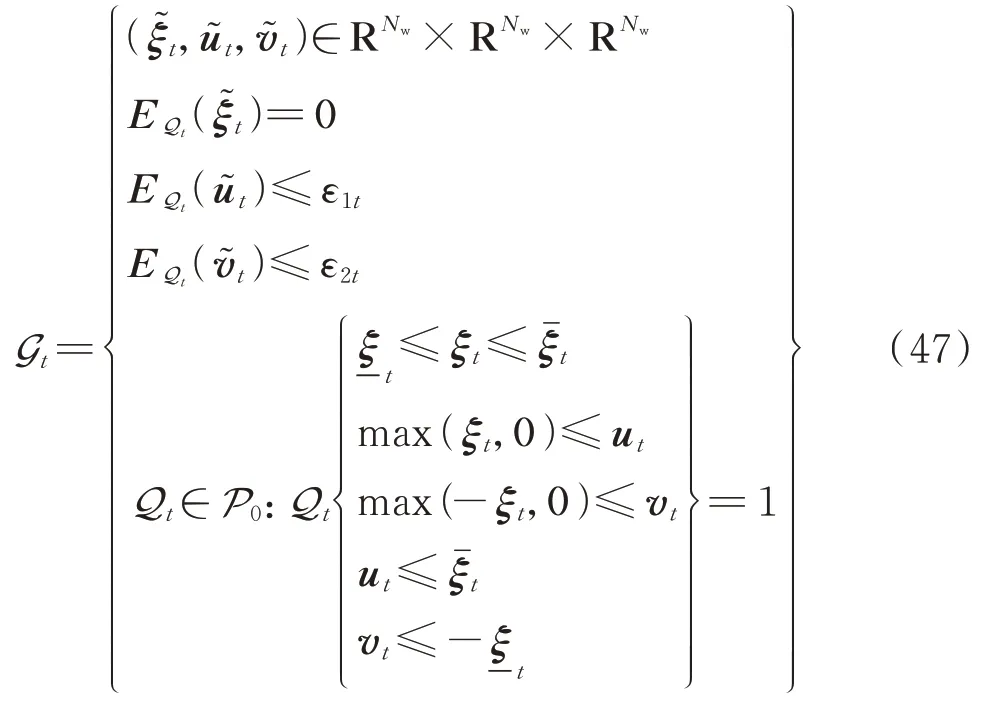
式中:Qt为不确定量和辅助不确定量的联合分布；EQt(·)表示求Qt分布下ξt的期望；ut和vt分别为u͂t和v͂t的某一具体值。

根据上述扩展模糊集Gt中的最后一行可得不确定量(ξt，ut，vt)的不等式约束的紧凑形式，即

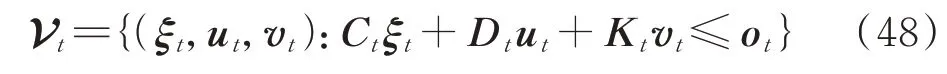
式中:Ct、Dt、Kt为常系数矩阵；ot为常系数向量。

结合式（47）的扩展模糊集，子问题式（45）中的实时阶段目标函数和约束条件可表示如下:

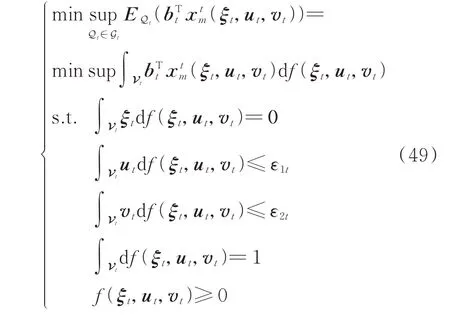
式中:f(ξt，ut，vt)表示不确定量的概率测度。

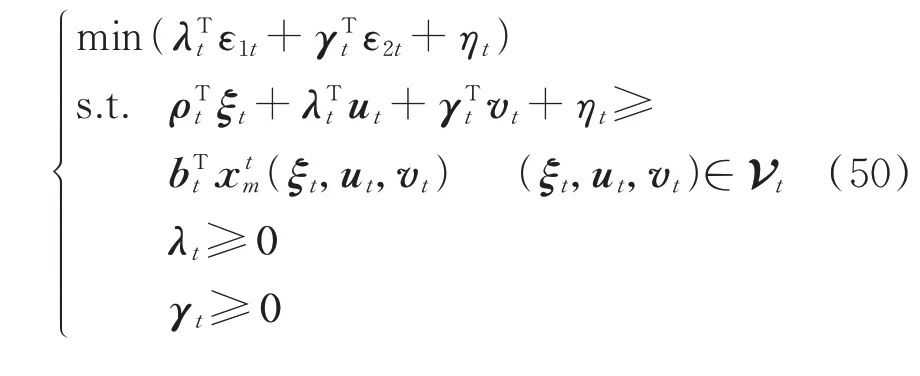
式（49）中约束条件与扩展模糊集Gt相对应。根据对偶理论，可将上述半无限优化问题转化为［21］:式中:ρt、λt和γt分别为与式（49）中前3 行约束对应的对偶向量；ηt为与式（49）中第4 行等式约束对应的对偶变量。

引入如下线性仿射规则描述实时阶段决策变量与不确定量之间的关系［22］:

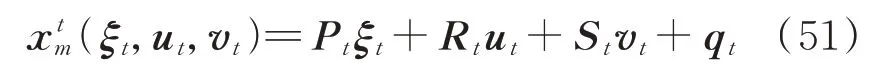
式中:Pt、Rt、St∈RNt×Nw为待求解的系数矩阵，其中Nt表示实时阶段决策变量的维度；向量qt∈RNt×1。

结合式（51），可将式（50）中约束条件转化为:

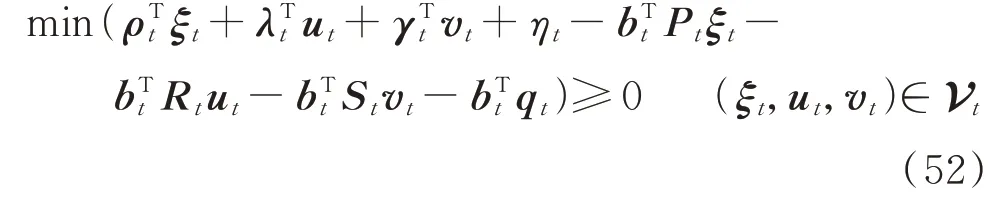
以上最小化问题中不确定量的约束即为式（48），设该不等式约束对应的对偶向量为πt。根据对偶理论可得式（52）的鲁棒对等形式［23］，即

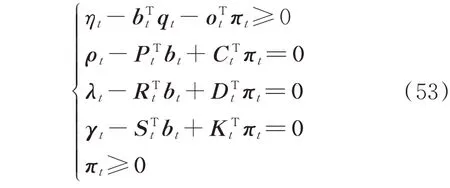
同理，子问题式（45）中含不确定量的约束可转化为如下鲁棒对等形式:

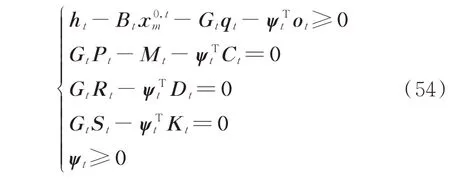
式中:ψt为式（48）不等式约束对应的对偶变量。

综上，式（45）的DRO 问题可转化为:

3.2 天然气网子问题求解

假设天然气网管道中气流方向已知且在日前调度中不发生变化，则管道潮流方程式（4）可表示为:

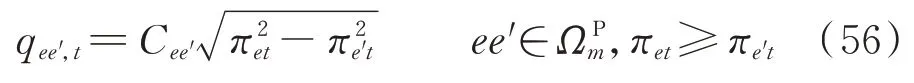
上式可转化为如下两个不等式约束:

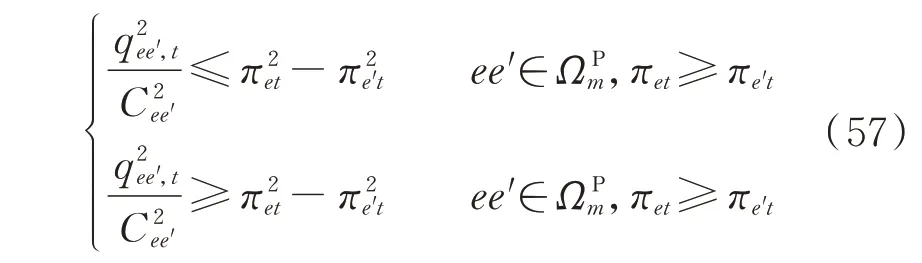
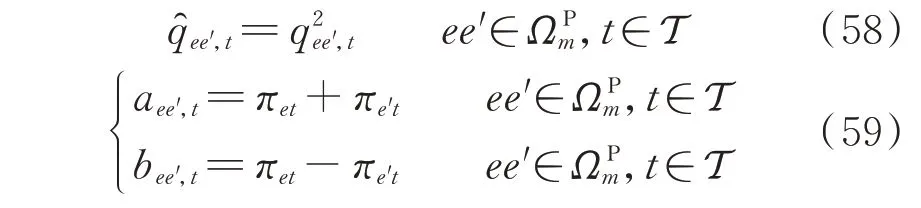
引入辅助变量νee′，t和ϕee′，t分别表示q̑ee′，t和aee′，tbee′，t的凸化逼近，则式（57）中第1 行约束可转化为如下二阶锥约束:

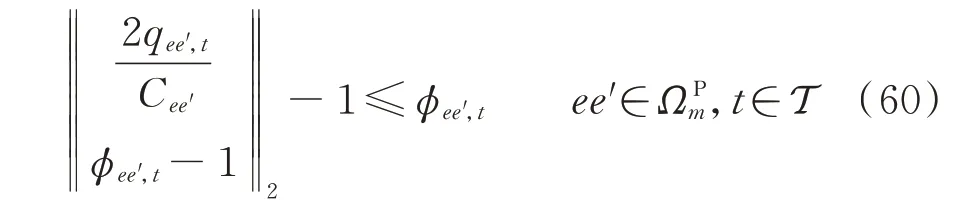
式（57）中第2 行约束可转化为［24］:

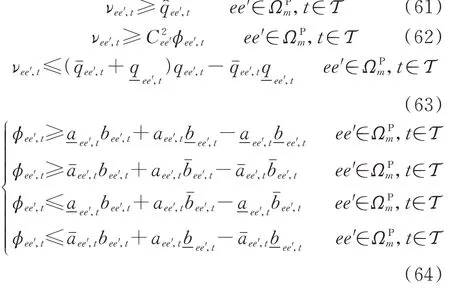
综上，可将含非线性约束的天然气网优化问题转化为二阶锥规划问题进行求解。

3.3 多区域分散协调问题的求解框架

针对多区域互联电-气耦合系统的协调优化问题，提出改进的ADMM 对其进行求解。

将区域m内天然气系统的决策变量ym定义为:

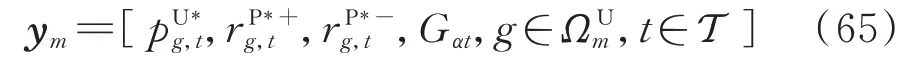
结合式（9）和式（23），可将配电网决策变量定义为:

多区域分散协调优化问题的一致性约束包括式（38）、式（41）—式（44），可将其写成如下紧凑形式:

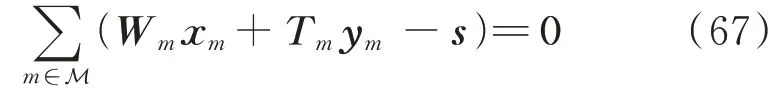
式中:Wm和Tm为常系数矩阵；s为常系数向量。

故该问题的增广拉格朗日函数可表示为［25］:

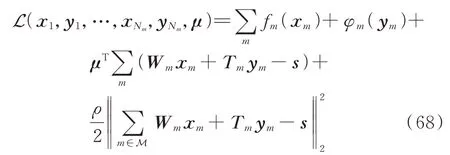
式中:Nm为区域个数；μ为与一致性约束对应的拉格朗日乘子向量；ρ为惩罚因子。

ADMM 是求解含两个可分离算子凸优化问题的有效分散式数学优化方法［26］，当区域数为1 时，单区域电气耦合系统的迭代格式如下:

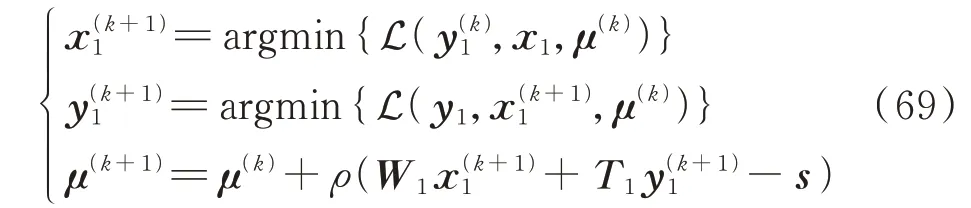
式中:k表示迭代次数；y1和μ分别为核心变量的原始部分和对偶部分；x1为区域中配电网决策向量。

然而，将ADMM 直接推广至含多个可分离算子的分散式优化问题时（m为2），其迭代格式如下:

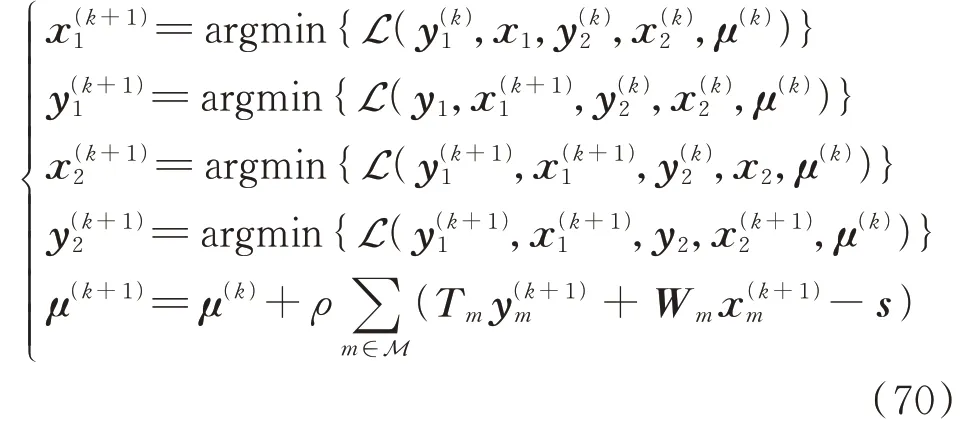
式中:y1、x2、y2为核心变量的原始部分；μ为核心变量的对偶部分。

由式（70）可看出，核心变量原始部分包含3 部分变量，在迭代中求解各部分变量时接收到的最新信息量是不同的，因此当可分离算子大于2 时，无法保证ADMM 内在的公平性。此外，虽然已有研究表明采用直接推广的ADMM 求解含多个可分离算子的实际工程问题是可行的，且能较快收敛，然而随着多区域协调优化问题规模的增大，每次迭代中逐一求解式（70）中所有子问题的耗时亦将增加。

因此，为兼顾算法的内在公平性及其高效求解，本研究结合适用于求解含多个可分离算子分散式优化问题的平行分裂增广Lagrange 乘子法（具体流程详见附录A），提出一种基于平行正则化改进的ADMM。其基本思路为:针对含多个可分离算子的分散式优化问题，选取某一子问题f1(x1)为首问题，则其余子问题被视为平行子问题。在每次迭代中，求解上述首问题获取其最新的决策变量x(k+1)1，依据原始ADMM 的交替性质将x(k+1)1传递给所有平行子问题，故任一平行子问题接收到的k+1 次迭代信息量相同，保证了算法内在的公平性。此外，为防止上述平等求解的子问题决策变量过于自由化导致算法不收敛，借鉴增广拉格朗日函数的思想，在平行子问题的目标函数中额外引入一个正则项对其进行自我约束。在每次迭代过程中，除首问题以外的平行子问题可并行求解以降低求解时间成本。综上，改进的ADMM 的求解步骤如下:

步骤1:设置迭代次数k=0，初始化各区域内配电网和天然气网子问题的决策变量，记为{y(0)m，x(0)m}，∀m∈M。拉格朗日乘子μ(0)=0，并设置惩罚因子ρ，收敛误差εP和εD。

步骤2:选取区域1 中配电网的DRO 子问题作为首问题，求得其最优决策如式（71）所示。

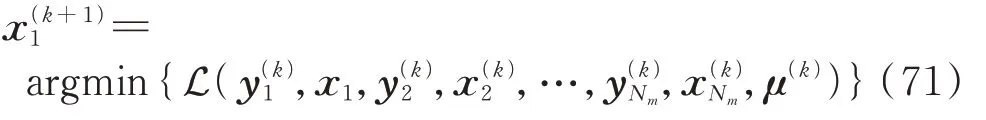
步骤3:并行求解多区域互联系统中余下的正则化配电网DRO 子问题和正则化天然气网子问题，其最优决策如下所示。

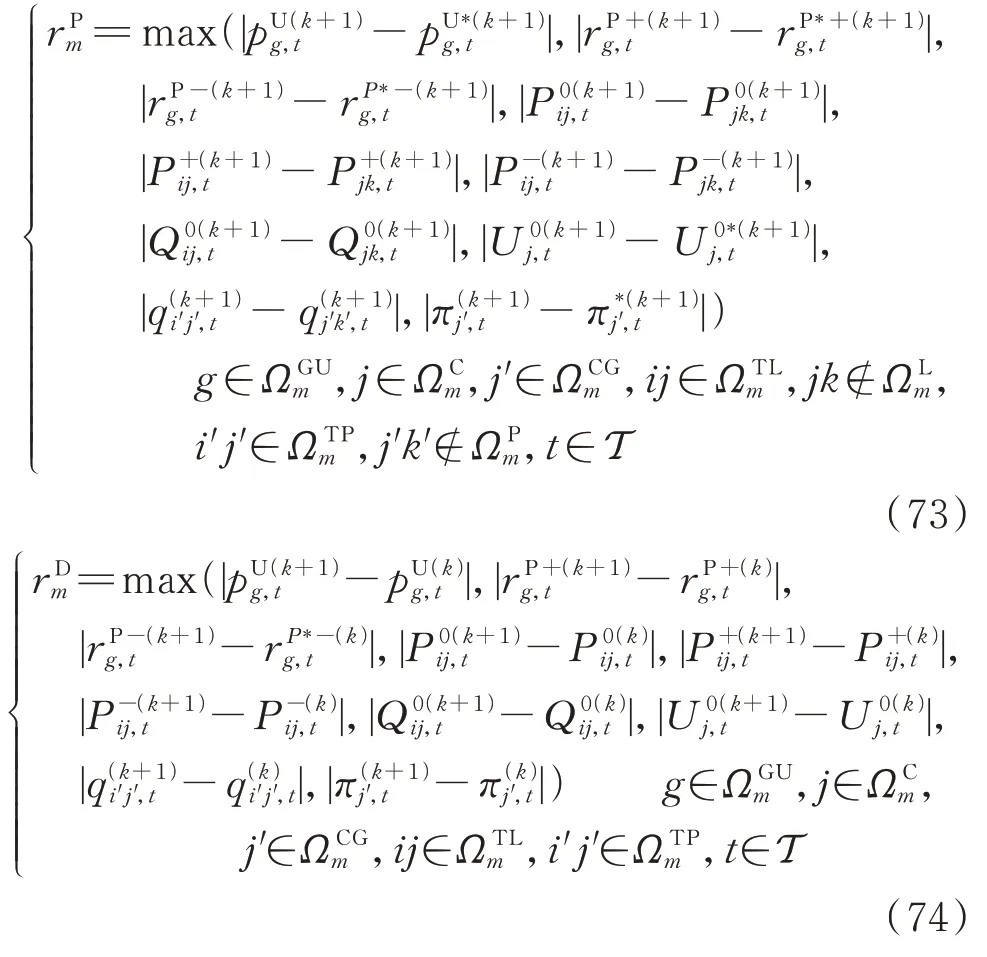
步骤4:计算如下原始残差和对偶残差。式中:rPm和rDm分别为原始残差和对偶残差。

当所有区域中的原始残差和对偶残差均满足max(rPm，m∈M)≤εP和max(rDm，m∈M)≤εD收敛条件时，迭代停止，获取多区域互联系统的最优调度决策{y(k+1)m，x(k+1)m}，m∈M。当收敛条件不满足时，进入步骤5。

步骤5:采用式（75）更新拉格朗日乘子，设置迭代次数k=k+1 并返回步骤2。

上述算法需要说明的是:在步骤2 选择区域1的配电网子问题作为首问题进行求解得到的决策变量x(k+1)1，该决策信息直接用于并行求解步骤3 中其他区域配电网子问题和所有区域天然气网子问题。因此，可选取跟其他子问题交换信息最多的子问题作为首问题，以便于更多决策信息传递。

本文中多区域电-气耦合系统的模型求解框架见附录B 图B1。

4 算例分析

4.1 系统描述

为验证所提模型和方法的有效性，本文选取3 个区域互联的电-气耦合系统进行仿真分析，其网络拓扑见图3。该系统中区域1 的配电网子系统分别通过联络线与区域2、3 内的配电网子系统连接，区域1 天然气网分别通过联络管道与区域2、3 内天然气网连接。3 个区域的配电网系统依次为改进的IEEE 33 节点配电网、IEEE 47 节点配电网和IEEE 56 节点配电网。各区域内配电网分别与7 节点天然气网通过燃气机组（G1、G2、G3）耦合，如图3 中蓝色虚线所示。配电网中发电机组接入情况见附录B 表B1，其中燃气、燃煤机组的运行参数及风电出力数据见文献［27］，区域1～3 中风电装机容量依次为1、2、1 MW，各区域配电网运行参数见文献［28］。

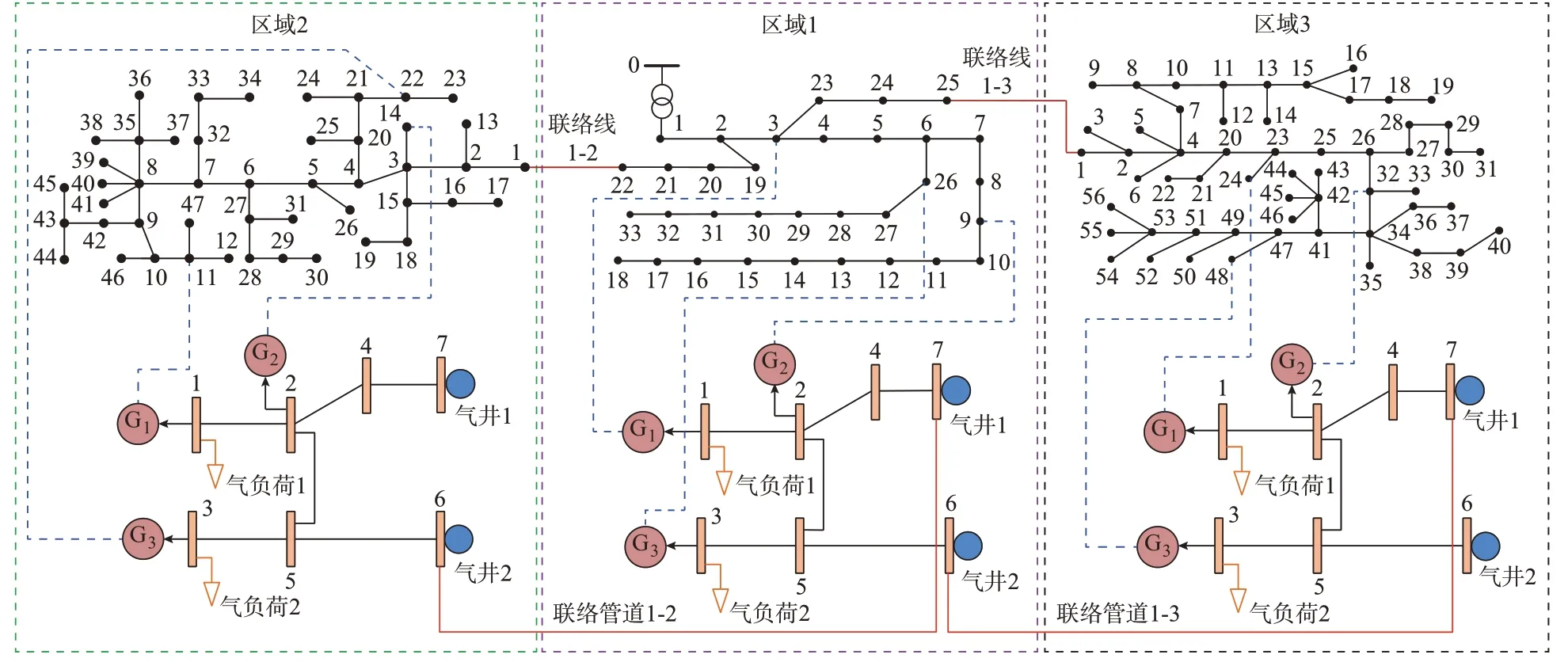
图3 多区域电-气耦合系统拓扑Fig.3 Topology of multi-area electricity-gas coupling system

配电网其他参数设置如下:节点电压限制设置-U=0.9 p.u.，=1.1 p.u.；线路传输功率限制L=2 MW，QˉL=2 Mvar；单位弃风、弃负荷惩罚价格cW=200 美元/(MW·h)，cL=1 000 美元/(MW·h)；联络线有功调整价格c=c=30 美元/MW。天然气系统运行参数见文献［29］，气源1 和2 的供气价格分别为c1=0.080 6 美元/m3，c2=0.059 4 美元/m3。分散式算法参数设置如下:εP=0.001，εD=0.001，ρ=1，σ=1。本文在MATLAB R2016a 平台调用CPLEX 12.6.0软件包对优化问题进行求解。

4.2 模式设计

针对多区域互联电-气耦合系统，本文设计如下不同调度模式进行算例分析，验证所提分散协调优化调度框架和DRO 方法的有效性。

模式1:不考虑风电出力不确定性的多区域电-气耦合系统优化调度。

模式2:考虑风电出力不确定性的多区域电-气耦合系统RO 调度。

模式3:考虑风电出力不确定性的多区域电-气耦合系统DRO 调度。

模式4:考虑风电出力不确定性和联络线有功备用的多区域电-气耦合系统DRO 调度。

模式1 仅考虑风电基准场景下的日前调度问题，即配电网子系统的目标函数为fm=F0(x0m)。故该调度问题是一个确定性分散式优化问题。模式2和3 考虑风电出力不确定性时，对配电网子问题分别采用传统RO 和本文所提DRO 方法进行建模求解，在日前和实时阶段联络线传输功率保持不变。其中，模式2 中采用的风电出力不确定集可表示为:Ut={ξ͂t∈RNw:-ξt≤ξ͂t≤ξˉt}。同所提DRO 模型的求解方法类似，可采用鲁棒对等变换转化为确定性优化问题求解。模式4 中考虑了联络线的有功备用以便于发挥多区域互联时配电网间联络线功率灵活可调的优势，即联络线传输功率基值作为日前阶段决策变量，其向上、向下调整量作为实时阶段决策变量。

4.3 仿真结果分析

针对上述4 种模式，采用所提改进ADMM 求解分散式协调优化调度问题，不同区域配电网运行成本见表1，天然气网运行成本见附录B 表B2。

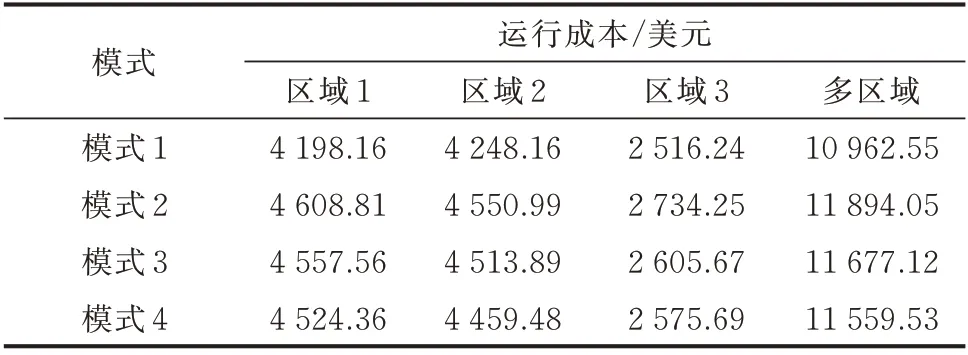
表1 不同模式下的配电网运行成本Table 1 Operation costs of distribution networks in different modes

由表1 可知:模式1 中不考虑风电不确定性时各区域的配电网运行成本最小。与模式1 相比，模式2中考虑风电不确定性的RO 调度决策所得配电网运行成本显著增大；模式3 中DRO 调度决策的各区域配电网运行成本比模式2 中均有所下降，配电网总运行成本降低了216.93 美元；与模式3 相比，模式4考虑联络线有功备用的DRO 调度决策时，区域1、区域2 和3 的运行成本分别减小了33.2、54.41、29.98 美元，其中区域1 的目标函数中计及联络线有功调节容量成本为116.15 美元。考虑联络线有功备用后，3 个区域总运行成本降低了117.59 美元。

由此可见，针对含风机的配电网子问题，本文采用的DRO 方法在原始不确定集中融入了风电预测误差的统计分布信息构造模糊集，可降低传统RO方法的保守性。此外，针对多区域互联的配电网协调优化问题，考虑联络线交换功率的不确定性可促进区域间有功备用共享及其灵活调整性能，使得互联配电网在应对风电不确定性时可获取更加经济的备用资源，从而进一步降低整体运行成本。

由附录B 表B2 可知，不同调度模式下天然气网子问题运行成本相差不大，其原因在于天然气网目标函数仅包括日前购气成本，考虑风电不确定性时只需对燃气机组提供向上、向下备用的可行性进行校验。

此外，本研究中不同模式下天然气网之间联络管道的输气量较小且相差不大。以下主要对不同模式下配电网之间联络线传输功率的差异进行分析。模式1～3 中配电网联络线传输的有功功率如图4 所示；模式4 中配电网联络线传输的有功功率可调区间如图5 所示。不同模式下联络线传输无功功率见附录B 图B2。

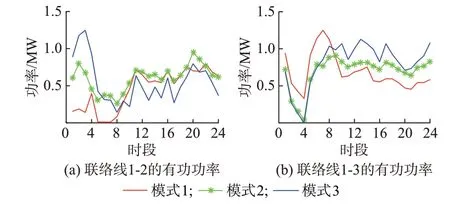
图4 联络线传输的有功功率Fig.4 Active power flows through tie-lines

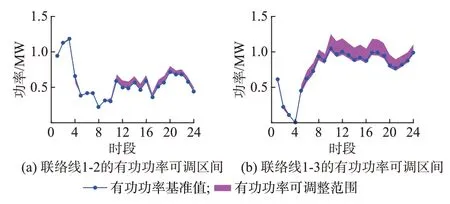
图5 联络线传输的有功功率可调区间Fig.5 Adjustable intervals of active power flows through tie-lines

由图4 可知，未考虑风电出力不确定性的模式1中联络线传输的有功功率的波动幅度最小，模式2和3 考虑风电出力的不确定性后联络线传输有功功率的波动幅度显著增大。由图5 可知，区域1 和3 之间联络线1-3 有功功率可调区间的宽度明显大于区域1 和2 之间联络线1-2 的有功功率可调区间。其原因在于:区域2 中的可调机组包括3 台燃气机组和2 台燃煤机组，而区域3 中仅配置3 台容量较小的燃气机组，故在风电实时出力较日前预测值出现大幅波动时，可通过联络线1-3 获取更多经济性更好的有功备用以降低整个互联系统的总运行成本。由附录B 图B2 可知:联络线在不同运行模式下传输的无功功率明显小于其传输的有功功率，在整个调度周期内的波动也较平稳，表明各区域内配电网主要通过该区域的机组无功出力的调整实现系统无功功率的就地平衡。

4.4 求解算法性能分析

采用基于平行正则化的改进ADMM 求解多区域互联电-气耦合系统分散协调调度问题，当调度时段为21 时，配电网之间耦合变量的变化曲线见附录B 图B3，其中图B3（a）中红色、蓝色曲线分别表示从区域1 内配电网流入耦合节点的有功功率和从耦合节点流入区域2 内配电网的有功功率，其余子图意义类似，不再赘述。所提算法的原始残差和对偶残差的对数收敛曲线见附录B 图B4。

从附录B 图B3 可看出，不同区域配电网流经耦合节点的有功功率在迭代初始时分别取其上下限，经历较大的振荡后在迭代末期达到一致；与耦合节点相关的无功功率和节点电压在整个迭代过程中数值相差不大。由图B4 可知，在迭代次数达到21 时，原始残差和对偶残差均小于设定的收敛值（0.001）。

为验证所提改进ADMM 的优越性，对4.2 节设计的4 种模式分别采用原始ADMM 进行求解，两种求解方法的迭代次数和求解时间见表2。

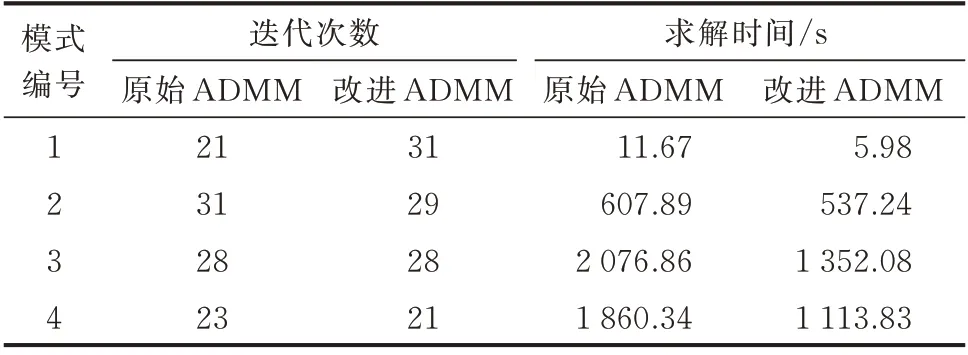
表2 不同求解方法的性能Table 2 Performance of different solving methods

从表2 可看出，模式1 下原始ADMM 的迭代次数明显小于所提改进ADMM，在模式2～4 中两种方法的迭代次数相差不大。不同模式下改进ADMM 的求解时间均小于原始ADMM 的求解时间。模式1 为确定性优化问题，运行时间最短；模式2 中传统RO 模型的运行时间较模式1 明显增大；模式3 和4 中构建了融合更多不确定量统计信息的DRO 模型，其求解时间进一步增加。随着配电网调度模型求解时间复杂度的增大，与原始ADMM 相比，改进ADMM 求解的高效性能愈发显著。其原因在于:原始ADMM 在每次迭代中需要对6 个子系统的优化问题依次进行求解，而所提改进ADMM在每次迭代中对选取的首问题进行求解后，可对其余5 个子系统优化问题并行求解，大大降低了一次迭代过程中的求解时间成本。此外，表2 中4 种模式采用以上两种求解方法时总运行成本最大相对差值仅为0.23%。综上可知，与原始ADMM 相比，改进ADMM 在保证求解精度的同时可提高求解效率，具有更好的工程实用性。

5 结语

针对多区域电-气耦合系统中存在的多种耦合关系及多重不确定性因素，本文提出一种基于平行正则化的改进ADMM 的分散协调优化框架。通过算例分析，可得如下结论:

1）与仅考虑风电出力边界信息的传统RO 方法相比，本文融合风电出力的历史分布信息建立不确定量模糊集，建立了配电网的DRO 调度模型，可有效降低传统RO 方法的保守性，提高调度决策的经济性能；

2）针对多区域互联的配电网联络线传输功率，构造基准有功功率值及其可调整区间，以适应风电出力在实时调度中的不确定性，促进了区域间有功备用共享及其灵活调整，可进一步提高整个系统运行的经济性和可靠性；

3）与原始ADMM 相比，采用基于平行正则化的改进ADMM 求解该多区域分散协调优化问题时具有更优越的求解性能。算例分析表明，随着子系统优化问题求解时间复杂度的提高，所提改进ADMM 通过子问题并行求解的策略可显著降低问题求解时间，验证了本文所提分散式方法的有效性和实用性。

需要指出的是，本文所提配电网DRO 模型的求解时间与传统RO 模型相比有明显增加，当配电网中考虑更多的源荷不确定因素时，所提模型求解的时间复杂度会进一步增大。下一步研究工作将致力于如何改善高维不确定量条件下模型的求解效率。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。