基于可靠性显式表达的交直流混合配电网规划方法

仲礼鹏，王梓耀，余 涛，刘易锟，彭秉刚，曾 江

（1. 华南理工大学电力学院，广东省广州市 510610；2. 广东省电网智能量测与先进计量企业重点实验室，广东省广州市 510610）

0 引言

配电网中，直流负荷和分布式可再生能源的规模日益增加，直流配电技术因其突出的供电能力、较强的可控性以及与负荷良好的兼容性受到了广泛关注［1］。目前，交流负荷依然是配电网中的主要负荷形式，因此，发展交直流混合配电网是最佳的过渡方式之一［2］。

近年来，交直流混合配电网方面的研究成果很多，但是主要侧重于优化调度方面［3-8］，规划方面的研究相对较少。文献［9］提出了一种考虑配电系统安装和运营成本的交直流混合配电系统随机规划模型。文献［10］提出了一种基于遗传算法的交直流混合配电网规划综合方法。文献［11］提出了一种交直流混合配电网双层规划模型，同时综合考虑源-网-荷-储的协同优化运行。上述文献针对交直流配网规划进行了不同方面的研究，提供了很多极具价值的解决方法及思路，但在构建配电网规划模型时尚未将系统可靠性作为目标或约束。文献［12-13］构建了考虑N-1 突发事件的交直流配电系统规划模型；文献［14-15］研究了计及预期未供应电量（expected energy not supplied，EENS）损失的交直流混合配电系统规划启发式多目标优化模型。然而，传统的可靠性评估算法（如解析法或蒙特卡洛算法［16-17］）包含复杂的拓扑搜索和逻辑判断，难以运用数学解析式的显式表达集成到配电网规划模型中，仅能采用启发式算法求解此类模型，难以保证规划模型的收敛性和最优性［18-19］，造成一定的经济性或可靠性损失。

近年来，部分学者克服了传统可靠性评估算法无法显式表达的困难，提出交流配电网的显式可靠性评估算法并将其应用于配电网扩展规划中［20-21］。在此基础上，文献［22］提出了线性化的显式函数表达式，在保证准确性的同时，提升了配电网规划的求解效率。然而，关于交直流配电网显式可靠性评估算法的研究仍是空白。

为弥补上述缺陷，本文提出交直流混合配电网的可靠性显式表达模型，得到评价配电系统可靠性常用的系统平均停电频率指数（system average interruption frequency index，SAIFI）、系统平均停电持续时间指数（system average interruption duration index，SAIDI）及EENS 的显式表达，并以此为基础，提出了一种考虑可靠性成本的交直流混合配电网混合整数线性规划（mixed-integer linear programming，MILP）模型。该规划模型通过引入可靠性激励机制，将规划方案的SAIFI 和SAIDI 对应的经济成本、EENS 对应的经济损失、配电网投资运营成本一并考虑到目标函数中，得到的规划方案能够很好地兼顾配电网的经济性和可靠性。最后，对13 节点案例进行仿真，验证了所提模型的有效性，比较了模型求解所得的交直流混合最优规划方案、交流最优规划方案、直流最优规划方案的各项重要指标，并分析了换流器故障率对规划结果的影响。

1 交直流混合配电网基本元件与结构

本文所研究的交直流混合配电系统的基本元件与结构如图1 所示［14］。基本元件包括交直流总线、负荷、断路器、分布式电源（DG）以及换流器，交流总线节点上的直流负荷和直流DG 需通过换流器与总线连接，直流节点同理。

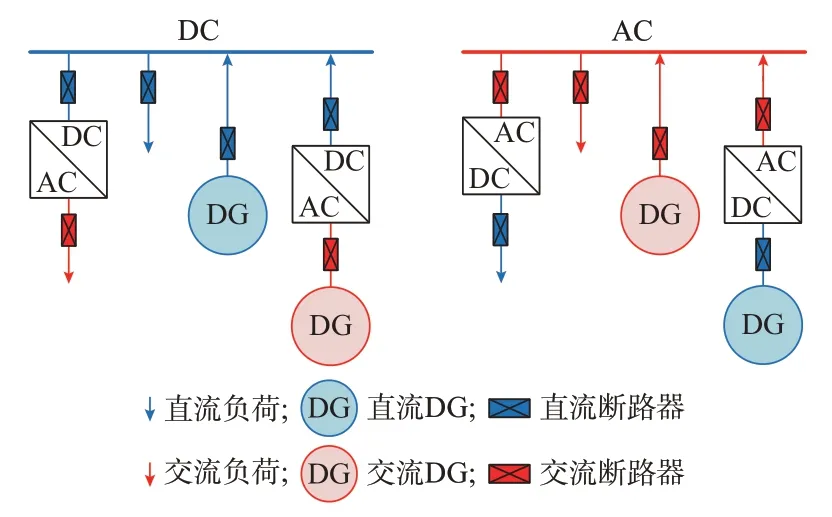
图1 交直流混合配电网基本元件与结构Fig.1 Basic components and structure of AC/DC hybrid distribution network

交直流混合配电网中连通节点间的支路类型因换流器存在而复杂多样，主要连接方式包括如图2所示的A、B、C、D 类。

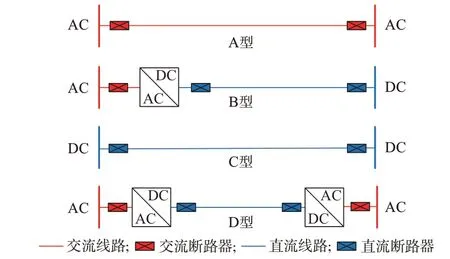
图2 4 类支路的结构示意图Fig.2 Schematic diagram of structure of four types of branch circuits

在A 型连接方式中，2 个交流总线节点间通过交流线路直接连接；在B 型连接方式中，交流总线节点和直流总线节点之间通过交流节点侧的电压源型换流器（voltage source converter，VSC）和直流线路连接；在C 型连接方式中，2 个直流总线节点间用直流线路直接连接；在D 型连接方式中，2 个交流总线节点间通过2 个VSC 用直流线路连接。但受限于目前换流器投建成本高、故障率高，且故障后修复时间长、难度大，在配电系统中相较于A 型连接方式，D 型连接方式的经济性和可靠性都更低［23］。因此，本文不考虑D 型连接方式。

2 交直流混合配电网规划模型

为兼顾配电系统的经济性与可靠性要求，本文所建立的交直流混合配电网规划模型以投资建设成本CI、运行维护成本CO以及可靠性相关成本CR的总和CT最小化为目标函数，表达式为:

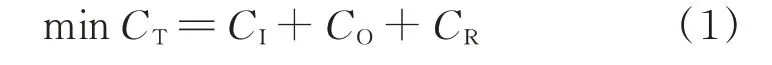
2.1 投资建设成本

目标函数中的投资建设成本包括线路、换流器、断路器的年均摊投建成本。为了方便计算，本文以支路和节点为模块计算整个配电系统的投建成本，表达式为:

式中:yb为线路b投建的0-1 决策变量，值为1 时表示投建，否则值为0；ρb，k为拟投建支路b建设为k型连接方式的0-1 变量，值为1 时表示建设该类型，否则值为0；Cb，k为支路b在k型连接方式下的线路投建年均摊成本；xi为节点i的投建类型0-1 决策变量，值为1 时表示待规划节点建设为直流节点，值为0 时表示待规划节点建设为交流节点；CACi和CDCi分别为节点i建设为交流节点时对应的投建成本和建设为直流节点时对应的投建成本；Bc为拟投建支路集合；ψp为待规划节点集合。

由图2 的结构可知，节点建设类型与最佳线路连接方式有如下对应关系:

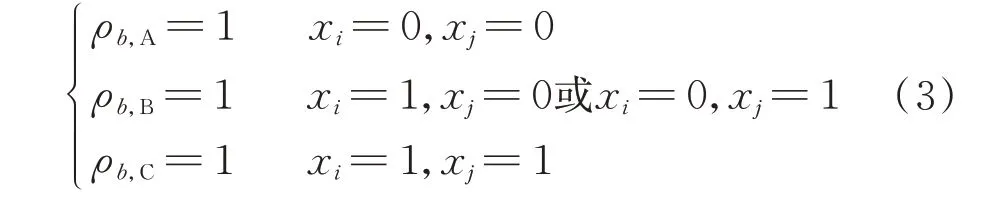
2.2 运营维护成本

系统运营维护成本CO包括线路的运营成本、向上级电网的购电成本Q以及DG 的运行成本ODG。其中，不同规划方案的网络损耗都体现在向上级电网的购电成本中。表达式为:

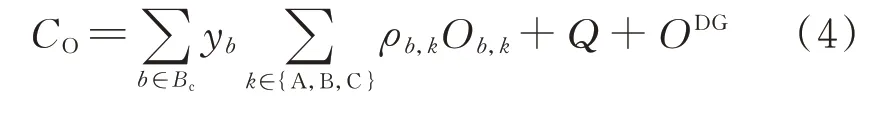
式中:Ob，k为支路b在k型连接方式下的线路年运维成本。

2.3 可靠性相关成本

目前，大多数研究在计及供电可靠性成本时大都只考虑EENS 的损失。然而，随着用户对供电可靠性的要求越来越高，基于SAIFI 和SAIDI 的可靠性激励机制逐渐被关注。在激励机制下，供电可靠性指标不能达到预定标准将受到处罚。同样的，若能达到预定的奖励标准将获得相应奖励。

通用的激励机制如附录A 图A1 所示，大致分为奖励区域、死区和惩罚区域，奖励区域和惩罚区域包括线性区和饱和区［22］。

本文在配电系统参与可靠性激励的前提下，将因停电造成的预期未供应能量带来的收入损失CEENS以及基于SAIFI 和SAIDI 这2 个可靠性指标的激励（分别表示为CSAIFI和CSAIDI）均考虑到可靠性成本中。可靠性激励可能是奖励（数值为正）或惩罚带来的损失（数值为负）。可靠性相关成本CR的表达式为:

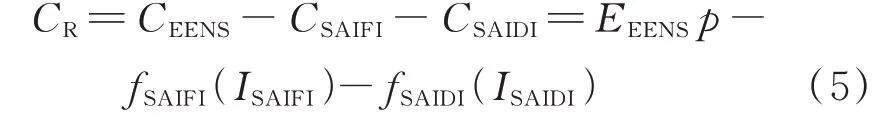
式中:EEENS为EENS 的值；p为电价；fSAIFI(·) 和fSAIDI(·)分别为可靠性指标SAIFI 和SAIDI 对应的分段激励函数；ISAIFI和ISAIDI分别为规划方案的SAIFI和SAIDI。

引入激励机制能够将评价配电系统可靠性的可靠性指标转化为与投建成本同一量纲的经济成本，从而指导规划结果，在追求经济性最优的同时，保证足够的可靠性。当然，激励机制也应当设计合理，文献［24］对如何设计激励机制参数进行了相关研究。

2.4 约束条件

在配电网规划模型中，需要对规划方案下的运行场景进行潮流校验，包括正常运行情况下的交直流潮流方程、节点电压约束、支路功率约束。

2.4.1 线性基尔霍夫电压定律（KVL）约束

对交直流混合配电网络中3 种典型连接线路构建KVL 方程为:

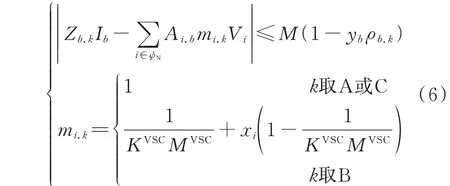
式中:Zb，k为支路b在k型连接方式下的阻抗值；Vi为节点i的电压；Ib为支路b线路电流；Ai，b为节点关联矩阵中第i行第b列对应的元素，表示节点i与支路b的连接关系，值为1 时表示支路远离节点，值为-1 时表示支路的参考方向朝向节点，值为0 时表示支路与节点无连接关系；ψN为节点集合；mi，k为节点i在k型连接方式下的电压系数；KVSC为与脉宽调制方式相关的换流器系数；MVSC为换流器脉宽调制比；M为足够大的正整数。

式（6）中利用Big-M法构建了一系列不等式，使得这些不等式只有在双变量乘积项yb ρb，k等于1 时才有意义，否则将被松弛。本文对类似问题均采用Big-M法处理。电压系数的推导过程见附录A 图A2、式（A1）至式（A4）。

2.4.2 线性基尔霍夫电流定律（KCL）约束

由于B 型连接线路和换流器的影响，负荷节点中交流节点和直流节点的KCL 方程有很大区别，表达式为:

式中:D和D分别为节点i的交流负荷需求和直流负荷需求；SCDG和SCDG分别为节点i所安装的交流DG 和直流DG 的容量；ηivt和ηrec分别为逆变器和整流器的换流效率；VACr和VDCr分别为交流节点和直流节点的额定电压；ηVSC为VSC 的换流效率；nb为支路b电流系数，B 型线路时取值为，否则为1，详细推导过程见附录A 图A3、式（A5）和式（A6）。

式（7）为直流节点处的KCL 方程，只有当节点i规划为直流节点（即xi=1）时才有意义，式（8）同理。

与上级电网相连的公共连接点满足的KCL 约束为:

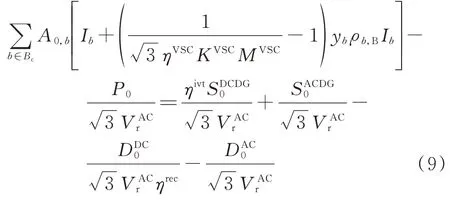
式中:A0，b为与上级电网的公共连接点关联矩阵中第0 行第b列对应的元素；P0为与上级电网相连的公共连接点向交直流混合配电网注入的功率；CDG和CDG分别为与上级电网的公共连接点所安装的交流DG 和直流DG 的容量；D和D分别为与上级电网公共连接点的交流负荷需求和直流负荷需求。

2.4.3 辐射状运行约束

对于拥有1 个变电站节点的N节点规模系统，要保证其辐射状结构需要满足2 个条件:1）必须有N-1 条回路；2）必须保证每个负荷节点都与变电站节点有连接关系，即不能存在孤岛运行状态［25］。事实上，当系统满足3.2 节的平衡约束时即已满足了条件2，还需要的约束为:

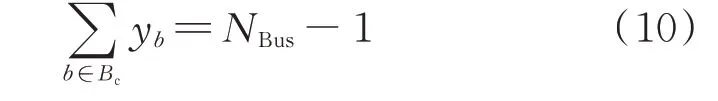
式中:NBus为包括公共连接点在内的总的节点数量。

2.4.4 支路电流约束

支路电流满足的约束为:

式中:I和I分别为交流线路和直流线路允许通过的最大电流值。

2.4.5 节点电压约束

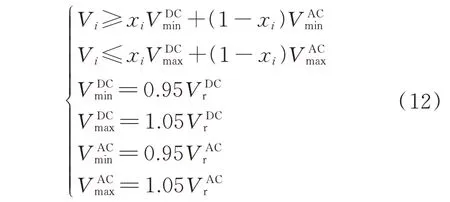
式中:V和V分别为交流节点电压的上、下限；V和V分别为直流节点电压的上、下限。

3 可靠性显式表达模型

可靠性指标SAIFI、SAIDI 以及EENS 的显式表达是式（5）可靠性成本能够融入规划目标的基础。本文基于虚拟潮流的思想推导得到了可靠性指标关于节点类型及线路投建决策变量的显式表达模型。

为了保证建立的交直流混合配电网可靠性显式表达模型求解的可行性以及适当地简化建模过程，本文基于以下实用假设。

1）交流断路器的故障率相较于换流器一般低一个数量级［26］，因此，本文暂不做考虑。本文可靠性评估只考虑线路、换流器以及直流断路器的一阶永久性故障，不考虑交流断路器故障或者系统多个元件同时发生永久性故障。

2）配电网一次网架开环运行，馈线及换流器两端均配置断路器，继电保护方案通过断路器动作实现。可靠性评估中忽略故障馈线上所有负荷点在继电保护动作期间的停电时间。

3）线路或换流器发生故障后，配套的断路器动作不影响上游负荷的正常运行；故障下游负荷须在故障处理完成后恢复正常运行；上游线路发生故障后下游部分负荷可由DG 供电。

4）当区域内存在重要负荷时，模型计算所用的节点负荷需求与用户数量按照失去该负荷对生命安全和经济性的影响程度进行加权计算［27］。

3.1 EENS 显式表达模型

在如图1 所示基本结构为基础的辐射状交直流配电网中，线路或线路上的VSC 发生故障都将导致下游所有节点与上游连接断开。除了部分负荷由DG 继续供能外，其余负荷将进入停电状态。节点与DG 或负荷连接处的整流器/逆变器发生故障将导致其直接相连的DG 或负荷无法正常运行。

基于此，可以从线路类型故障和节点类型故障2 个方面考虑元件故障导致的预期未供应电量，具体表达式为:

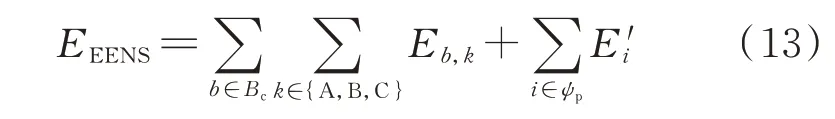
式中:Eb，k为支路b在k型连接方式下因故障导致的下游缺供电量；E′i为因节点i与负荷或DG 相连接的换流器发生故障而导致的负荷停电量与DG 缺供电量。Eb，k和E′i可以分别通过式（14）和式（15）计算得到。

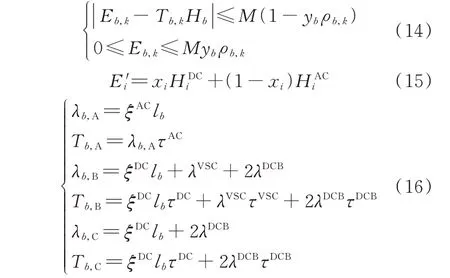
式中:Hb为因线路b故障而导致的下游负荷功率缺失量；Tb，k为线路b在k型连接方式下的等效故障修复时间；Tb，A、Tb，B、Tb，C分别为线路b在A、B、C 型连接方式下的等效故障修复时间；lb为线路b的长度；λb，A、λb，B、λb，C分别为在A、B、C 型连接方式下等效故障率；ξAC、ξDC分别为交流线路和直流线路单位长度的故障率；λVSC为VSC 的故障率；λDCB为直流断路器的故障率；τAC、τDC、τVSC分别为交流线路、直流线路、VSC 的故障修复时间；τDCB为直流断路器的故障修复时间；HACi和HDCi分别为节点i建设为交流节点和直流节点时因节点端元件故障损失的等效负荷需求［27］。

在式（14）中，当待规划支路投建为k型连接方式（即yb ρb，k=1）时，第2 个不等式将被松弛，Eb，k被第2 个不等式约束为Tb，k Hb；否则（即yb ρb，k=0），Eb，k被约束为0。式（15）在节点类型不同时赋予E′i不同的表达式。

上述等式中还有至关重要的一个变量Hb需要求解，考虑到上游故障后分布式电源依然可以为部分负荷继续供电，Hb应为下游负荷与DG 供电之差，且需保证其为非负数。因此，可以结合Big-M法构建的约束表达式为:

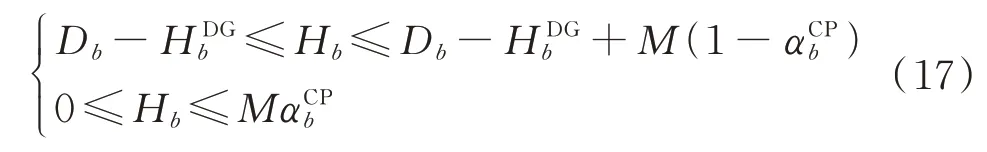
式中:Db为支路b下游的总的最大负荷需求；HDGb为支路b下游的所有DG 计及换流效率的供电容量；为辅助二值变量，用以保证Hb非负。

当Db＞HDGb时，只有α取1 才能满足所有不等式约束，此时，Hb被约束为Db-HDGb，即线路b故障而导致的下游负荷功率缺失量等于下游最大负荷需求总量与DG 供电量的差值；当Db＜HDGb时，只有αCPb取0 才能满足所有不等式约束，此时，Hb被约束为0，不会出现Hb取负数这种不符合实际的情况。

针对式（17）中引入的新变量Db，引入非负变量和，其中，和分别为支路b正、负方向的虚拟负荷需求潮流。根据实际情况，须保证和只能有一个取非0 值，这个条件可以通过引入辅助二值变量αDb构建约束表达式满足。

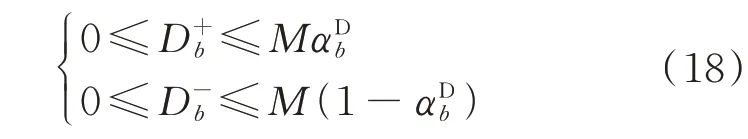
于是，Db的约束表达式为:

式中:L和L分别为根据负荷重要程度进行加权计算的交流节点和直流节点的等效负荷需求；L和L分别为公共连接点下的交流类型和直流类型的等效负荷需求；G0为与上级电网相连的公共连接点下游的等效总负荷需求。

式（20）针对每个待规划节点构建了类似KCL平衡方程的虚拟负荷潮流平衡方程，式（21）则是针对与上级电网连接的公共连接点建立了虚拟负荷潮流平衡方程。式（22）的不等式约束使得当待规划支路b不投建时，Db取值为0。

3.2 SAIFI/SAIDI 显式表达模型

相似的，可以分别从线路元件故障和节点端元件故障进行与SAIFI 和SAIDI 相关指标ISAIFI和ISAIDI的计算，表达式为:

式中:Fb，k和Jb，k分别为因支路b在k型连接方式下的线路或元件故障将会导致的下游用户停电次数和停电时长；′ 和分别为因节点端与负荷连接处的元件故障导致的用户停电次数和停电持续时长；F和FDCi分别为节点端建设为直流和交流节点时，节点端故障对应的用户停电次数；J和J分别为节点端建设为直流和交流节点时，节点端故障对应的用户停电时长；NLb为支路b发生故障时下游受影响的等效用户数量；Ni为节点i下计及负荷重要程度加权计算得到的等效用户数［27］。

考虑到线路故障时下游的DG 依然可以为部分负荷供电，因此，式（31）和式（34）中的NLb并不直接等于支路b下游的用户数量。当支路b下游安装了DG 时，应估计故障时DG 的可供电用户数量，表达式为:

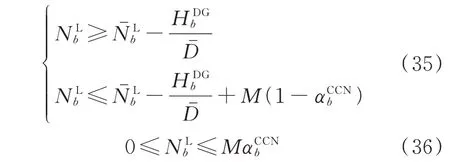
4 模型处理

当前模型依然存在绝对值项、双线性项、逻辑表达等非线性部分，为了得到MILP 模型，需要对模型进一步线性化处理。

4.1 逻辑判断线性化

式（3）对应的逻辑关系式可以用式（42）的线性表达式等价表示。

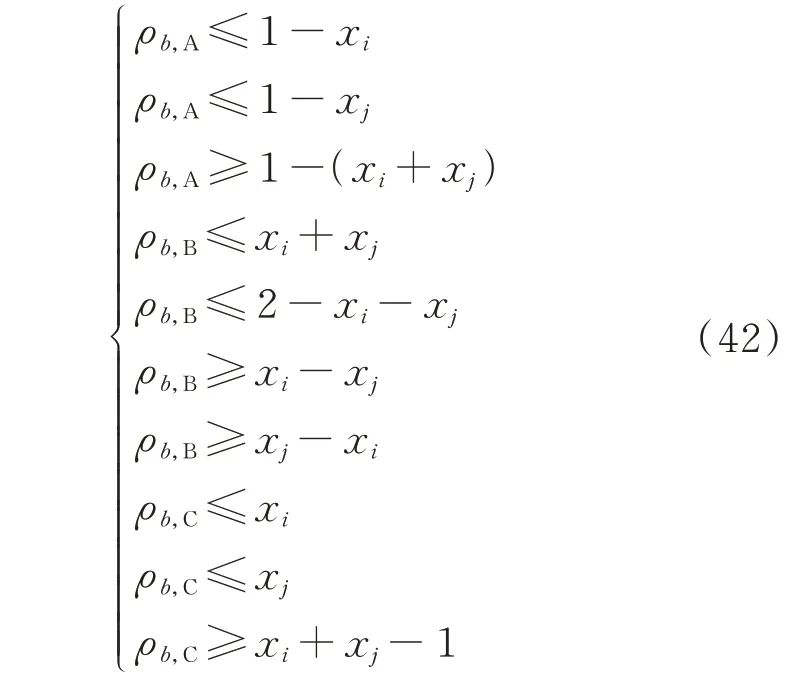
4.2 双线性乘积项线性化

模型中包含的双线性乘积项都可以采用McCormick 包络方法进行线性化处理［28］。即对形如ω=xy的乘积项，将其线性化的约束为:

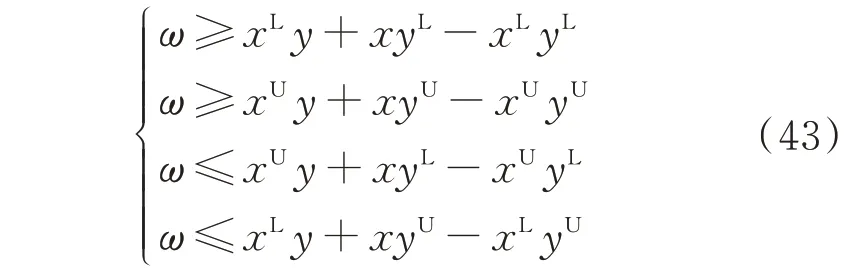
式中:xL和yL分别为变量x和y的下限；xU和yU分别为变量x和y的上限。

模型存在的其他非线性项为:

1）计算线路中VSC 安装容量时的线路电流绝对值项；

2）计算激励成本的分段线性函数。

以上非线性部分的具体处理方法见附录A 式（A7）至式（A12）。

5 算例分析

对本文建立的交直流混合配电网MILP 模型，在Python 环境下进行编程实现，调用Gurobi 9.0.3求解器，运行环境中，CPU 型号为Intel Core i7-6700，主频为3.40 GHz，内存容量为8 GB。

5.1 算例与模型参数

本文算例模型的拓扑如附录A 图A4 所示。除公共连接点确定为交流节点外，其余12 个节点都是待规划节点，类型未定。案例中共有26 条拟投建支路。

拟投建支路数据、节点信息、配电网中交直流线路及换流器的平均故障率与故障修复时间、供电可靠性激励机制参数以及交流线路和直流线路的各参数见附录A 表A1 至表A5［9，14，22］。

中压交直流混合配电网算例交流节点的额定电压为4.16 kV，直流节点的额定电压为6.8 kV；整流器、逆变器、VSC 的换流效率均为98%，脉宽调制比均为0.96，容量裕度均为10%；换流器均采用正弦波脉宽调制方式，换流器系数取 3/8；换流器单位投建成本均取170 美元/（kV·A）；系统安装的所有交直流断路器均采用2 kA 额定电流的断路器，造价为每台26 000 美元［14］；直流分布式电源发电成本为209 美元/（MW·h），补贴为106 美元/（MW·h）；交流分布式电源发电成本为92.2 美元/（MW·h），无补贴；年均电价取80 美元/（MW·h）；折现率为5%；所有元件的有效使用年限为20 年。

5.2 不同规划方案比较分析

为研究交直流混合配电网中兼顾经济性和可靠性的最佳规划方案，本文对比了交流规划方案（即所有节点类型决策变量x均为0）、直流规划方案以及交直流混合规划方案在经济性和可靠性上的优缺点。

3 种规划方案的各项主要投资的年均摊成本以及可靠性指标如表1 所示。其中，方案1、方案2 和方案3 分别为交流、直流和交直流混合规划方案。为精简篇幅，3 种方案的拓扑如附录A 图A5 所示，各方案下换流器规划容量如表A6 和表A7 所示。

表1 规划结果对比Table.1 Comparison of planning results

由表1 可知，交直流规划方案的投建成本以及规划总成本都低于交流和直流规划方案。其中，投建成本相较于交流规划方案和直流规划方案分别节省了1.74%和3.26%。可靠性方面，由于现有的换流设备（尤其是整流器）以及直流断路器故障率相对较高，故障修复时间也较长。因此，接入整流器较少的直流规划方案在可靠性方面相对优秀，SAIFI 相较于交流规划方案和交直流规划方案分别降低了8.11%和7.11%。

另外，从表中可以看出，本文所用的可靠性激励机制参数不适合交直流网络，导致各方案最优解的SAIFI 和SAIDI 均落在可靠性激励函数的饱和区。因此，直流规划方案的可靠性指标虽然优于交流方案，但二者的可靠性成本相差甚小。

5.3 换流设备故障率变化影响分析

目前，换流设备的高故障率是限制直流配电网发展的一个重要因素。随着电力电子技术的发展，换流设备的故障率逐步下降，这对未来的规划结果也必然有较大的影响。

在5.2 节中，已经体现出附录A 表A4 的可靠性激励机制参数并不适用于本文的交直流算例。因此，根据5.2 节各最优方案的可靠性指标数值，本节对可靠性激励机制参数进行了相应修改（见表A8），并基于修改后的可靠性激励机制研究了换流设备故障率变化对规划方案可靠性指数的影响，结果如图3 所示。

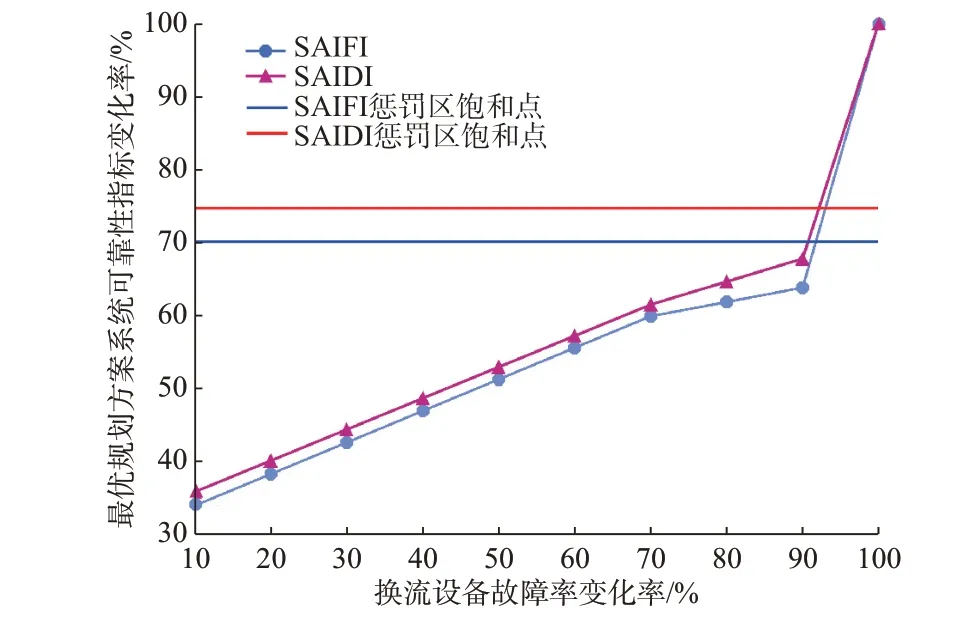
图3 可靠性敏感度分析结果Fig.3 Result of reliability sensitivity analysis

由图3 可知，最优规划方案的可靠性指数SAIFI 和SAIDI 对换流设备故障率变化的敏感度略有不同，但趋势基本一致，均随着故障率的降低而减小。

修改后的SAIFI 和SAIDI 的激励机制惩罚饱和点分别取2.50 和10.00，转化成比例分别对应图3 中的蓝线和红线。由图3 可知，当前故障率下，最优方案的可靠性指标落在惩罚饱和区。因此，目标函数中的可靠性成本对求解结果失去影响，得到的最优规划方案可靠性极差。当可行解中有能够达到惩罚饱和区以下的解时，目标函数中的可靠性经济成本将会促使模型求解得到可靠性较好的规划方案。

另外，从图3 中的斜率变化可以看出，当故障率降低至当前所取值的70%以下时，求解得到的最优规划方案的拓扑不再发生变化，与当前所取值的70%情况下得到的最优规划方案拓扑一致。新激励机制下，敏感度分析求解得到的各最优规划方案的拓扑见附录A 图A6 至图A9，VSC 参考规划容量见表A9。

5.4 模型求解效率分析

本文在13 节点算例下对3 种规划场景进行了规划模型构建。场景1 为交流配电网规划；场景2 为直流配电网规划；场景3 为交直流混合配电网规划。各场景下规划模型分别利用本文方法和遗传算法进行求解。其中，遗传算法的种群规模、交叉概率和最大代数分别设置为50、0.7 和4 000，最优解与求解效率如表2 所示。

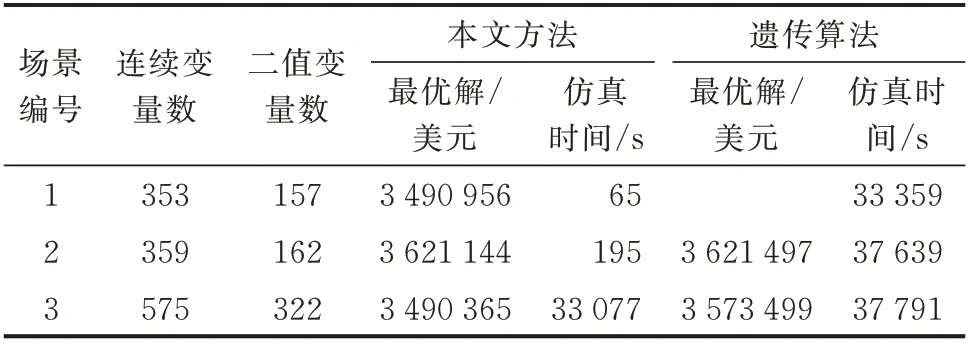
表2 模型复杂度与求解效率对比Table 2 Comparison of model complexity and solution efficiency

由表2 可知，交直流混合配电网MILP 模型相较于传统的交流配电网规划模型，无论是模型复杂度还是算法求解效率都面临更大的挑战。同时，对比本文方法与遗传算法的最优解及仿真时间也验证了启发式算法难以保证求解结果全局最优的缺陷以及求解效率上的不足。

6 结语

本文提出了交直流混合配电网的可靠性显式表达模型与线性潮流约束，并结合线性化处理技巧提出了一种计及可靠性成本的交直流混合配电网MILP 模型，为考虑可靠性的交直流混合配电网网架规划优化提供了有效的解决方案和分析思路，主要包括:

1）针对中压交直流混合配电网混合整数规划模型中的众多非线性部分进行线性化处理，将模型简化为MILP 模型；

2）提出交直流混合配电网中主要的可靠性指标EENS、SAIFI 和SAIDI 的显式线性表达模型。并将EENS、SAIFI 和SAIDI 相关的可靠性成本计入目标函数，构建能够较好兼顾经济性与可靠性的MILP 模型；

3）比较了交直流配电网场景下交直流混合规划方案、交流规划方案和直流规划方案的重要评价指标。结果表明，在交直流混合配电网系统中交直流混合规划方案综合评价最优，但目前相较于交流方案所具备的优势较小；

4）研究了换流器故障率降低对求解得到的最优规划结果的影响。结果表明配电系统的可靠性会随着换流设备故障率降低而显著提高。同时，最优规划结果的拓扑也会因故障率降低或者可靠性在规划中的权重变化而改变。

在后续的研究中，将进一步考虑交直流系统中换流器的不同控制模式及运行状态，并研究高效的模型求解算法，使交直流配电网规划模型能够适应不同运行场景，提升模型的鲁棒性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。