高效二阶注意力对偶回归网络的超分辨率重建

廉炜雯，吴 斌，张红英，李 雪

1.西南科技大学 信息工程学院，四川 绵阳 621010

2.特殊环境机器人技术四川省重点实验室，四川 绵阳 621010

人类主要通过视觉获取信息，图像质量的好坏决定了绝大多数基于视觉领域的应用效果。这也是超分辨率重建技术兴起，并日益发展的原因所在，高质量的图像也是顺利开展大部分图像处理研究与应用的前提[1-2]。单幅图像超分辨率（single image super resolution，SISR）重建方法主要分为以下三类：基于插值的方法[3-4]、基于重建的方法[5]和基于学习的方法[6-7]。虽然前两种方法比较简单，但重建后的图像质量不高，还伴有一定程度的模糊和伪影现象。近年来，基于深度学习的SISR方法因其优异的重建性能成为本方向的研究重点，其基本思想是通过学习算法建立高、低分辨率图像之间的映射关系来指导图像复原工作[8-9]。Dong等[10]首次将深度学习应用于超分辨率重建领域，并提出端到端映射的SRCNN网络。在此基础上，Dong等[11]又提出了基于SRCNN的改进算法FSRCNN，该算法能更快速、更清晰地重建低分辨率图像。Kim等[12]提出了基于残差的深层网络结构VDSR，该网络采用较大的学习率加速收敛速度，同时采用自适应梯度剪裁来解决梯度爆炸和梯度消失问题。Kim等[13]提出了DRCN方法，将深度递归思想应用在SISR领域，达到卷积层间的参数共享，在加深网络的同时，尽可能不增加网络参数量。Li等[14]提出了SRFBN方法，将人类视觉系统中常见的反馈机制应用到SISR中，来改进具有高级信息的低级表示，在具有约束的循环神经网络（recurrent neural network，RNN）中使用隐藏状态来实现反馈方式，该反馈模块旨在处理反馈连接并生成强大的高级表示，为自上而下的反馈流提供高级信息。

虽然深度学习近年来在SISR重建领域取得了显著成就，但仍然存在以下不足：（1）超分辨率重建是一个典型的病态问题，其高分辨率（high-resolution，HR）图像与低分辨率（low-resolution，LR）图像的映射关系是非线性的，就会使得可能的函数映射空间过大，模型出现自适应的问题。（2）现阶段基于卷积神经网络（convolutional neural networks，CNN）的SISR方法在重建过程中没有充分利用原始LR图像中的信息，从而导致性能相对较低。（3）大多数基于CNN的SISR方法没有充分学习更具辨识性的高级特征表示，很少利用中间层固有的特征相关性，阻碍了CNN的表达能力。针对以上问题，本文提出了一种高效二阶注意力对偶回归网络（efficient second-order attention dual regression network，ESADRNet），该网络通过在原始网络的基础上增加对偶回归任务缩小映射空间，找到LR和HR之间的最优映射关系。此外，本文还采用高效二阶通道注意力机制（efficient second-order channel attention，ESOCA）来更好地学习特征间的相关性，通过高于一阶的特征统计来自适应的调整特征，使网络专注于更多的特征信息，并增强网络的学习能力。采用多级跳跃连接残差注意力模块（multi-level skip connection residual attention group，MLSCRAG）和共享源跳跃连接（shared skip connection，SSC）结构的叠加，更好地利用LR图像中的高频信息，以产生更好的重建效果。实验结果表明，与SRCNN、FSRCNN、VDSR、DRCN和SRFBN-S网络相比，本文方法的重建效果更好。

1 高效二阶注意力对偶回归网络基本块设计

1.1 对偶回归网络

现阶段，大多数图像超分辨率重建网络都只包含原始回归任务，即LR到HR的映射关系，但SISR是一个典型的病态问题，LR图像与HR图像的映射关系具有不适定性，即存在无限多的HR图像可以通过下采样的方式获得相同的LR图像，这就使得LR到HR的映射空间过大，模型出现自适应的问题。本文的对偶回归网络可以很好地解决这一问题，该网络既包含LR到HR的映射关系又包含HR到LR的映射关系。对偶回归网络的主要思路是利用机器学习中的对称属性来构建网络，通过反馈对机器学习任务的效果进行加强和指导[15-16]。对偶回归网络主要可以分为两个任务：原始回归任务和对偶回归任务，该网络的示意图如图1所示。

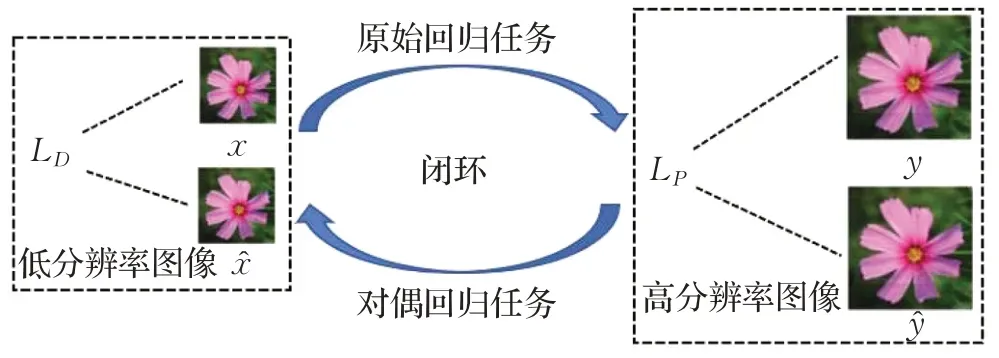
图1 对偶回归网络结构示意图Fig.1 Schematic diagram of dual regression network structure

从图1可以看出，对偶回归网络将超分辨率重建分为LR图像域和HR图像域，建立两者之间的闭环映射关系，相互学习和促进，提高模型的泛化能力。具体理论依据如下，设E(P,D)=E[LP(P(x),y)+λLD(D(P(x)),x)],并且Ê(P,D)是其经验损失。函数空间Hdual无穷大，设LP(P(x),y)+λLD(D(P(x)),x)为X×Y在区间为[0,C]上的映射。对于任意误差δ＞0,其概率至少是1-δ,并且泛化误差E(P,D)中所有(P,D)∈Hdual,通过拉德马赫尔复杂度得到模型的推广界[17]：

其中，N是样本数量是对偶学习的经验拉德马赫尔复杂度。B(P,D)为对偶回归任务的推广界，可由以下公式表示：

由此得出B(P,D)≤B(P)。其中B(P)(P∈H)是有监督学习的推广界，用拉德马赫尔复杂度表示为

以上公式表明，对偶回归网络的推广界依赖于函数空间Hdual的拉德马赫尔复杂度，根据公式（1）可知，在监督学习中对偶回归网络比传统网络的推广界更小，从而有助于实现精确的SISR。

1.2 多级跳跃连接残差注意力模块（MLSCRAG）

目前大多数CNN网络模型的深度和复杂度增加，这就使得网络的计算和收敛难度加大，为了能更好地提取具有区别性的特征表示，利用各个特征之间的相关性。本文提出的MLSCRAG由M个多级跳跃连接残差块（MLSCR）和一个高效二阶通道注意力模块（ESOCA）构成，经过第g个MLSCRAG模块后的Fg用公式可表示为：

其中，Wg是相应的权重，如图2所示的MLSCRAG在训练时能绕过丰富的低频信息，使网络更关注具有区别性的特征表示。此外，在每个MLSCRAG的末端都加入一个高效二阶通道注意力模块（ESOCA），这就让重建网络更加专注于特征的相互依赖性。

图2 MLSCRAG模块结构示意图Fig.2 Schematic diagram of MLSCRAG module structure

MLSCRAG模块与典型的注意力机制模块相比有以下三点优势：（1）典型的注意力机制模块前期大多采用简单的卷积残差块来提取图像特征信息，而本文提出了MLSCR，能加强特征信息间的相互关联，提取更丰富的特征信息。（2）本文采用由全局协方差池化构成的ESOCA模块对串联的MLSCR模块提取到的特征进行进一步的处理，典型的注意力机制只利用全局平均池化的一阶特征信息进行特征提取，只能获取单个通道的平均值，而二阶统计量相较一阶统计量能更有效地关注更具辨识性的特征表示。（3）典型的通道注意力机制采用两个具有非线性全连接（fully connected，FC）层来捕获非线性的跨通道交互信息，通过降维来控制模型的复杂度，但捕获所有通道之间的依赖关系并非必要，本文采用卷积核大小为k的快速1D卷积实现一种不降维的局部跨通道交互策略，能更有效地捕获跨通道交互，既能保证效率又能保证有效性。

1.3 多级跳跃连接残差块（MLSCR）

大多数卷积神经网络中的残差块都只是对特征向量多次堆叠卷积处理，并没有很好地利用特征信息之间的相关性，从而使得上下文特征信息关联性较差，网络性能欠佳。针对以上问题，本文设计了多级跳跃连接残差块（MLSCR），其结构如图3所示。

图3 MLSCR模块结构示意图Fig.3 Schematic diagram of MLSCR module structure

由图3所示，一个3×3卷积层、PReLU激活函数层和α倍跳跃连接组成一个子残差块，两个子残差块和β倍跳跃连接组成一个MLSCR模块。设其输入为x，经过第一个和第二个子残差块的输出分别为y1和y2，经一个MLSCR后的输出为y3，则分别可由下式表示：

从输出y3可以看出，当输入x经过MLSCR模块后不仅可以得到经第二个基本残差块G2(x)处理后的输出，还可以得到经第一个基本残差块G1(x)处理后的输出和输入x。

以上为单个MLSCR模块的输出结果，若将多个MLSCR模块串联，经过第三个和第四个子残差块的输出分别为y4和y5，经第二个MLSCR模块后的输出为y6，则分别可由下式表示：

通过经第二个MLSCR模块后的输出y6可以得出，相邻两个MLSCR模块的子残差块中的卷积层都要对前面每个卷积层的特征向量进行卷积，然后再输出。这就充分利用了相邻子残差块内部卷积层间特征向量的相关性，使网络能提取到更丰富的特征信息。

1.4 高效二阶通道注意力模块（ESOCA）

研究表明，只利用全局平均池化的一阶特征信息限制了网络的表达能力，而深度卷积神经网络中的二阶统计量比一阶统计量更有效地关注具有区别性的特征表示，但这会使网络的复杂度增加，为了克服性能和复杂性权衡的矛盾，本文设计了一种高效二阶通道注意力（ESOCA）模块，其结构如图4所示。

图4 ESOCA模块结构图Fig.4 ESOCA module structure diagram

ESOCA模块主要由协方差归一化和高效通道注意力机制两部分组成。给一组H×W×C的特征图f=[f1,f2,…,fC]，其中C个特征图的尺寸为H×W，将该特征图重构为具有C维s=WH个特征的特征矩阵X，然后样本协方差矩阵可以计算为：

归一化后的协方差矩阵表征了通道特征的相关性，然后将归一化后的协方差矩阵作为全局协方差池化的通道描述符。如图4所示，设通过缩小得到通道统计量z∈RC×1，然后计算z的第c维统计量可表示为：

其中，HGCP(·)表示全局协方差池化函数，这也是本文ESOCA模块与其他注意力机制模块的区别之一。常用的一阶池化操作有平均池化、最大池化、随机池化和全局平均池化等。平均池化即对邻域内特征点求平均，能很好地保留图像背景信息，但会使图像变模糊；最大池化即对区域内的特征点取最大值，能很好地保留图像纹理特征，但在一定程度上影响了梯度回传；随机池化只需对特征图中的元素按照其概率值大小随机选择，即元素值大的被选中的概率也大，与最大池化不同，并非只取最大值元素，该池化方法简单，泛化能力更强；全局平均池化则是直接把整幅特征图进行平均池化，然后输入到softmax层中得到对应的每个类别的得分，该方法大幅度降低了网络参数，减少了过拟合现象，但上述池化方法都属于一阶池化，只能提取到一阶特征，而无法探索高层次的特征。全局协方差池化是用一个二阶的统计方法来替换一阶的全局平均池化，即将一阶的均值替换为二阶的协方差，解决了小样本高维度难以统计的问题并且有效利用了协方差矩阵的几何结构，探索更多的特征分布，并获取高于一阶且更具辨别性的特征表示。

给定聚合特征y∈RC，在不进行降维处理的情况下，通道注意可以通过下式计算得到：

其中，W是参数量为C×C的矩阵，本文使用带状矩阵Wk来学习通道注意，该方法能更有效地捕获本地跨通道交互信息，Wk可以表示为：

由上式不难看出，Wk矩阵中涉及k×C个参数，该方法相较于其他方法可以进行快速高效的运算，其主要原因有以下几点：（1）该方法参数量通常小于用群卷积方法实现的参数，避免了群卷积方法中不同组之间的完全独立性。（2）深度可分离卷积方法没有考虑跨通道交互信息，使模型的性能不佳。（3）用FC层实现虽然考虑了跨通道交互，但是需要大量的参数，导致模型的复杂性较高，特别是对于较大的通道数。

对于式（15），yi的权重仅考虑yi与其k个邻域之间的关系计算得到，并使所有通道共享相同的学习参数，即：

这种不降维的局部跨通道交互策略可以通过卷积核大小为k的快速1D卷积来实现，充分利用全局协方差池化聚合信息的特征依赖性，在显著降低模型复杂度的同时保持网络性能，其函数表示如下[18]：

式中，C1D表示1D卷积，式（17）中的方法由只调用涉及k参数的高效通道注意（efficient channel attention，ECA）模块。该方法避免降低维度，有利于学习更有效的通道注意，比采用两个FC层的通道注意力机制效果更好[19]。其交互的覆盖范围（即1D卷积的卷积核大小k）与通道维数c成正比，本文k=3。最后就可以得到通过通道注意力机制缩放后的特征图：

式中，ωc和fc分别表示第c个通道的比例因子和缩放后的特征图。

2 网络框架设计

2.1 总体网络结构

本文的超分辨率卷积神经网络是基于U-Net网络[20]构建的，该模型由两部分构成：原始回归网络和对偶回归网络。原始回归网络主要由下采样模块和上采样模块构成，下采样模块采用步长为2的卷积层，FReLU激活函数和卷积层串联，该下采样模块能利用像素级的建模能力提取更复杂的细节信息。再基于多级跳跃连接残差注意力模块（MLSCRAG）、共享源跳跃连接（SSC）和亚像素卷积构建渐进式上采样网络，使网络具有更强大的特征表达和相关特征学习能力，让网络在训练时更关注具有区别性的相关特征，提取更丰富的特征向量相关信息；最后利用与原始回归网络下采样模块相同的结构构成对偶回归网络，来约束映射空间，寻找最优重建函数。结构如图5所示。

2.2 原始回归网络

原始回归网络（图5中的黑线）由上采样（图5左半部分）和下采样（图5右半部分）模块组成，网络根据不同的比例因子，分别包含lbs个基本块，其中s表示比例因子，每个基本块包括一个下采样模块和一个对应的上采样模块，即有2个基本块用于4×上采样网络（如图5），有3个基本块用于8×上采样网络。

图5 ESADRNet网络结构图Fig.5 ESADRNet network structure diagram

2.2.1 下采样模块

原始网络参考U-Net网络的下采样部分来设计，由步长为2的卷积层、FReLU激活函数和卷积层构成，如图5所示。激活函数中的空间不敏感是阻碍视觉任务实现显著改善的主要原因，自适应的捕获空间相关性成为激活函数需要解决的重点问题。本文采用FReLU激活函数作为下采样模块的激活层。FReLU[21]是2020年由旷视提出的一种新的激活函数，实现像素级空间信息建模且性能优于其他激活函数。为了使深度神经网络更好地重建复杂的细节信息，FReLU采用漏斗激活可视化任务，可以使用像素级的建模能力轻松获取复杂的信息，有助于提取物体的精细空间布局，通过添加可忽略的空间条件开销，将激活函数扩展到二维激活。其表达式为：

式中，t(·)是一个依赖于空间上下文的二维漏斗状空间条件，本文将二维空间条件设置为ParamPool，即表达式可写为y=max(x,ParamPool(x))，参数池化窗口为3×3。

2.2.2 上采样模块

与基本U-Net网络不同，在上采样部分本文采用B个MLSCRAG和SSC相结合的基本模块及上采样器构成，如图5所示。每个MLSCRAG还包括M个MLSCR模块和一个ESOCA模块，如图2所示。该模块能很好地解决由于神经网络深度过深导致的梯度消失和爆炸的问题，不仅有助于深层神经网络的训练，而且还可以从LR图像中绕过丰富的低频信息，使网络集中在拥有更多纹理细节的高频信息重建上。MLSCR模块通过在基本的残差块中加入含有不同权值的多级跳跃连接来增加上下文信息的关联性，增强网络性能。ESOCA模块主要是通过二阶特征统计和高效通道注意力机制来自适应地调整通道特征，使网络拥有更强大的特征表示和特征相关学习能力，以获得更具辨识性的特征表示。本文的上采样器由一个卷积层和一个像素重洗（Pixel-Shuffle）层[22]组成，其中像素重洗层起到压缩空间维度、扩张分辨率维度的作用。设B是MLSCRAG的数目，M是MLSCR的数目，F是基本特征通道数目。对于4×网络本文设置B=30,M=10,F=16,对于8×网络本文设置B=30,M=10,F=8。此外，在ESOCA模块中，本文用1D卷积实现一种不降维的局部跨通道交互策略，并设置1D卷积的卷积核k为3。在MLSCR模块中，本文设置其参数分别为α=0.1,β=0.1。

2.3 对偶回归网络

对偶回归网络（图5中的灰线）是对HR图像进行多次下采样得到不同比例系数的LR图像，对偶回归任务的目的是学习一个降采样操作，这比学习上采样映射的原始任务简单得多。因此，该对偶回归网络和原始回归网络中的下采样模块相同，只有两个卷积层和一个FReLU激活函数层，其计算成本比原始模型低得多，但在实践中效果良好，可以减少可能的函数映射空间，找到最优的函数映射。

2.4 损失函数

本文采用对偶回归网络，引入了对LR图像的附加约束。除了学习LR到HR图像的映射外，本文还学习了HR到LR图像的映射。原始和对偶回归任务可以形成一个闭环，并提供相互监督的训练模型P和D。如果P(x)是正确的HR图像，那么下采样得到的图像D(P(x))在理论上也是非常接近输入的LR图像x。给定一组含有N对样本的数据集其中xi和yi表示成对数据集中的第i对LR和HR图像，其训练损失函数可表示为：

其中，LP和LD分别表示原始回归任务和对偶回归任务的L1损失函数，λ为控制对偶回归损失的权重。经过多次实验对比，在训练中设置λ=0.1，具体实验结果见3.2.2小节所示。

3 实验与结果分析

3.1 实验配置

3.1.1 实验环境配置

本次实验采用Facebook推出的Pytorch深度学习框架，实验操作系统为Ubuntu18.04，CUDA版本为CUDA10.0，CPU为Intel i5-9600KF，GPU为NVIDIA GeForce RTX 2060 SUPER，显存大小为8 GB。

3.1.2 数据集

实验采用DIV2K和Flickr2K数据集进行神经网络的训练，分别包括800和2 650张训练图片。通过随机截取RGB输入低分辨率图像的48×48大小图像与对应的高分辨图像区域作为配对训练数据，并分别将图像进行旋转90°、180°和270°，并对应进行翻转，得到每张图像的变体，达到增加训练数据的目的。本文使用4个常用单幅图像超分辨率测试集在2×比例因子、4×比例因子和8×比例因子分别进行测试和比较，包括Set5、Set14、BSD100和Urban100。

3.1.3 实验参数设置

本方法使用Adam优化器进行参数优化，设置β1=0.9,β2=0.999，并将minibatch设置为32。学习率初始化为10-4，然后每100个epochs减小一半。

3.1.4 评价指标

本文采用客观评价方法和主观评价方法对图像重建效果进行评价，客观评价方法包括两种常用的图像质量评价指标：峰值信噪比（peak signal to noise ratio，PSNR）和结构相似性（structural similarity，SSIM）。经过模型重建后输出的高分辨率重建结果与标签高分辨率图像在YCbCr空间计算Y通道上的PSNR值和SSIM值，从而更客观地表明本文算法优于其他算法。PSNR通常用于测量图像压缩等有损变换的重建图像质量，数值越大，劣化程度越小，重建效果越好。SSIM表示图像的相似性程度，SSIM(x,y)的取值范围为[0，1]，比较的x、y两幅图像越相似，SSIM的值就越大，重建后的结果就越接近真实图像。

3.1.5 模型细节

网络使用Conv（1，1）和Conv（3，3）分别表示卷积核大小为1×1和3×3的卷积层。使用Convs2表示步长为2的卷积层。采用一个卷积层和一个亚像素卷积层构成上采样器，来提高特征图的比例大小。此外，使用h和w来表示输入LR图像的高度和宽度。因此，对于4×模型，输出图像的形状应为4h×4w。模型设计细节如表1所示。

表1 4×模型设计细节Table 1 4×model design details

3.2 对比实验与模型分析

3.2.1 网络实时性及参数规模

如表2所示，本文在4×放大比例因子下对模型参数量以及图像在不同的基准数据集下总重建时间进行实验。该网络模型的总参数量是10.8×106，在Set5数据集上的平均重建速度是0.34 s/张；在Set14数据集上的平均重建速度是0.37 s/张；在BSD100数据集上的平均重建速度是0.236 2 s/张；由于Urban100数据集中的图像分辨率较高，重建难度较大，模型的平均重建速度是1.086 6 s/张。综上所述，该模型可以达到实时处理的效果。

表2 4×模型上网络实时性及参数规模Table 2 4×network real-time performance and parameter scale on model

3.2.2对偶回归损失权重λ对网络性能的影响

经过多次实验来研究对偶回归损失权重λ对网络性能的影响，由表3可知，将λ从0.001增加到0.1时，对偶回归损失逐渐变得重要，并增加了监督能力。若进一步将λ增加到1、2、5和10，对偶回归损失项将远比原始回归损失重要，并阻碍最终性能。为了在原始回归和对偶回归之间取得良好的平衡，本文选取λ=0.1对模型进行训练。

表3 4×模型上对偶回归损失权重λ对网络性能的影响Table 3 Impact of dual regression loss weight λ on network performance on 4×model

3.2.3 高效二阶通道注意力模块（ESOCA）有效性

为了验证高效二阶通道注意力模块（ESOCA）的有效性，本文在4×模型上用Set5测试集分别对算法的不同模块进行消融实验，具体结果如表4所示。Ra表示有30个含有10个MLSCR的MLSCRAG模块的实验模型，该模型的PSNR值达到31.98 dB。Rb表示在Ra模型的基础上，在每个MLSCRAG模块间加入SSC的实验模型，性能可以从31.98 dB提升到32.04 dB，主要原因是共享源跳跃连接在重建时绕过来自LR图像的低频信息。Rc表示在Ra模型的基础上在每个MLSCRAG模块末端加入一个一阶通道注意力模块（FOCA），网络性能从31.98 dB提升到32.10 dB。Rd表示在Ra模型的基础上在每个MLSCRAG模块末端加入一个二阶通道注意力模块（SOCA），网络性能从31.98 dB提升到32.14 dB。Re表示在Ra模型的基础上在每个MLSCRAG模块末端加入一个高效二阶通道注意力模块（ESOCA），网络性能从31.98 dB提升到32.18 dB。Rf、Rg和Rh分别表示在Rc、Rd和Re的基础上加入SSC后的网络性能。由此可以看出ESOCA模块的有效性，二阶统计量比一阶统计量更有效的关注具有区别性的特征表示，提升网络性能，用1D卷积实现的不降维的局部跨通道交互高效注意力机制可以更好地提高网络性能。由表可见，Rf、Rg和Rh模型的性能均在一定程度上优于Rc、Rd和Re模型的网络性能，而Rh模型在实验中的性能最好，故在本文网络中采用该网络对数据集进行训练。

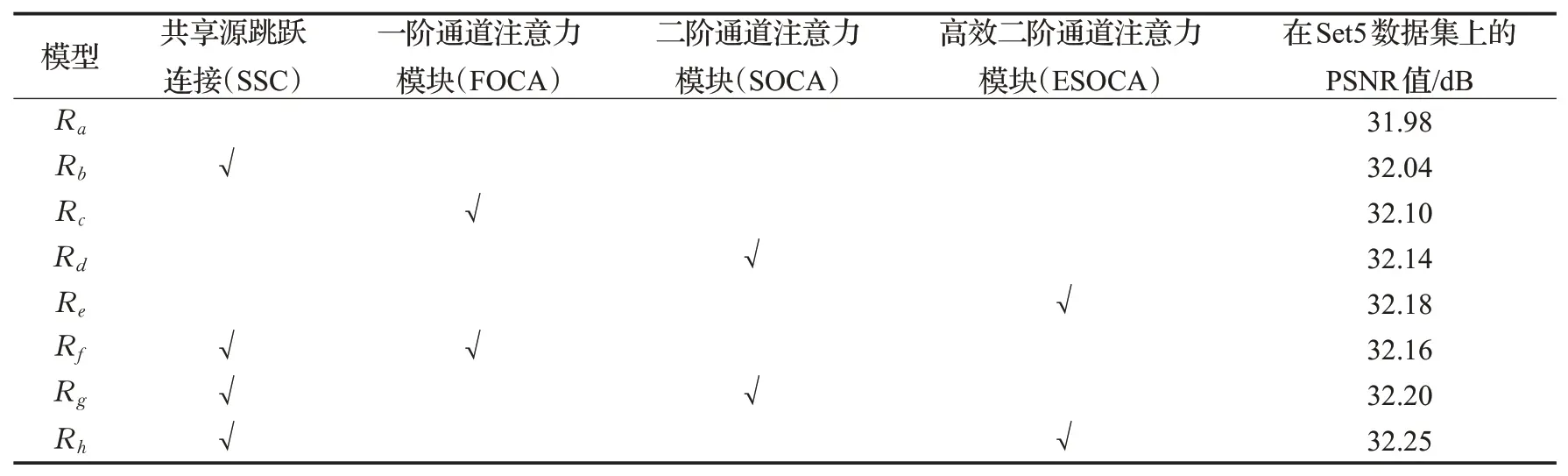
表4 4×模型上高效二阶通道注意力模块（ESOCA）有效性Table 4 Effectiveness of efficient second-order channel attention module（ESOCA）on 4×model

3.2.4 高效二阶通道注意力模块（ESOCA）实现成本

如表5所示，对4×比例因子下MLSCRAG模块末端分别加SOCA和ESOCA模块的模型参数量，在Set5基准数据集上总测试运行时间和PSNR值进行实验对比。MLSCRAG模块末端加SOCA模块的模型参数量是14.5×106，在Set5基准数据集上总测试时间是2.48 s，PSNR值是20.20 dB。本文的ESOCA模块通过1D卷积避免降低维度，比采用两个FC层的通道注意力机制效果更好，网络模型参数量减少了25.52%，在Set5基准数据集上总测试时间提高了0.78 s，即平均重建速度提高了0.156 s/张。而PSNR值也由32.20 dB提高到32.25 dB。

表5 4×模型上高效二阶通道注意力模块（ESOCA）实现成本Table 5 Realization cost of efficiency second-order channel attention module（ESOCA）on 4×model

3.2.5 算法对比实验

为了验证本文方法的有效性，本文选取了5种已有的基于深度学习的SISR方法，SRCNN、FSRCNN、VDSR、DRCN和SRFBN-S，与传统的Bicubic算法，在2×、4×和8×的比例因子下分别进行实验对比，结果如表6所示。从表中不难看出，无论是在2×、4×还是8×的比例因子下，在不同的测试集下，本文算法的客观评价指标PSNR和SSIM均处于领先。

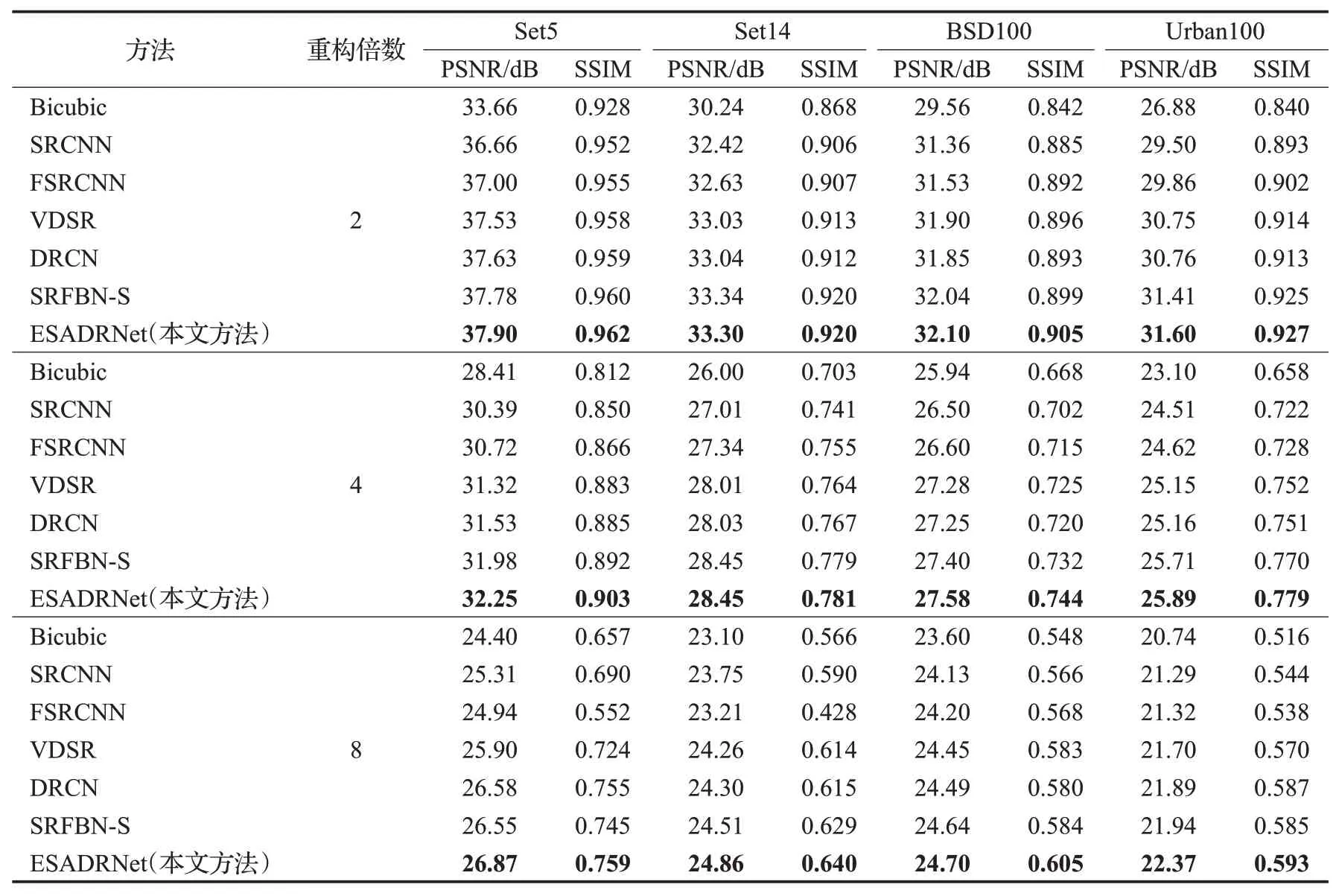
表6 不同算法PSNR和SSIM指标对比Table 6 Comparison of PSNR and SSIM indicators of different algorithms

本文还对不同算法的主观视觉效果进行了对比测试，图像来自Set5、BSD100和Urban100测试集，结果如图6所示。为了方便观察重建效果，文中选取了各图像中容易辨别的细节特征，例如图6（a）中的眼睫毛部分，从图中明显可以看出本文方法重建的图像睫毛根根分明，十分接近原图；图6（b）中的飞机螺旋桨部分，其他算法都未能很好地重建出图像的边缘细节信息，只有本文方法重建出来的图像在细节纹理部分比较清晰；图6（c）中的公交车内饰部分，其他算法都有明显的模糊和伪影现象，只有本文方法重建出来的图像边缘更锐利；图6（d）中的建筑物细节，只有本文方法重建出来的图像细节信息更丰富。因此，定量数据与定性视觉效果，均表明低分辨率图像通过本文算法重建后的效果整体优于所对比的重建算法。

图6 与不同算法的视觉效果对比Fig.6 Comparison of visual effects with different algorithms

4 结束语

本文设计了一种基于高效二阶注意力对偶回归网络（ESADRNet）的单幅图像超分辨率结构，该网络引入对偶回归任务能有效缩小LR-HR图像的映射空间，通过共享源跳跃连接（SSC）和多级跳跃连接残差块（MLSCR）绕过LR图像中大量的低频信息，使网络专注于学习上下文特征表示间的相关性。此外，除了利用空间特征相关性外，本文还采用高效二阶通道注意力（ESOCA）模块，通过全局协方差池化来学习特征相关性，以获得更具辨别性的特征表示。FReLU作为网络的激活函数层，使网络具有像素化建模能力。通过大量对比实验表明本文方法不论从客观指标还是主观视觉上，均优于对比方法。