基于S 分量指数加权H 分量的圆形直方图阈值法

张智豪，范九伦

（西安邮电大学通信与信息工程学院，西安 710021）

0 概述

彩色图像分割是图像分析、图像理解和计算机视觉领域的一个重要课题［1-3］。然而，使用最广泛的RGB 颜色空间［4］并不适合彩色图像分割任务，原因是R（红）、G（绿）、B（蓝）3 个分量具有高度相关性。对于HSI 颜色空间而言，H（色调）、S（饱和度）和I（强度）是线性无关的，H 和S 分量反映了颜色属性，I 分量是对光线强度的描述。HSI 模型［5-6］的3 个分量能够准确量化像素点的颜色信息，在以色彩为主要特征的图像分割任务中［7-9］具有较大优势。

HSI 颜色空间可以用一个圆锥模型来表示，像素的色调（H）值由该点到圆面上圆心的直线与水平线所形成的圆心角表示，饱和度（S）大小可以由像素点与所在圆面的圆心之间的距离表示，且其随距离的增大而增大，亮度（I）大小可以由像素点所在圆面与圆锥顶部之间的距离表示，且其随距离的增大而增大。H 分量通常被用来在宏观上区分某一种颜色，每种颜色对应特定的波长，其反映了颜色的“质量”。S 分量指颜色的纯度，即颜色的深浅程度，表示一种纯色被白光稀释的程度，在通常情况下，颜色越鲜艳，饱和度越高。

H 分量具有周期（循环）特性，用直方图表示时是一个圆形直方图。基于H 分量的圆形直方图可以实现彩色图像的图像检索［10-11］和阈值分割［12-14］。然而，仅使用H 分量的圆形直方图在进行图像检索或阈值选取时，饱和度（S）低的像素会导致色调（H）直方图出现大量的“毛刺”，使得直方图看起来参差不齐，不够平滑，不易理解与分析，图像分析效果受这些无意义“毛刺”的影响很大。为此，HANBURY［15］提出构建S 分量加权H 分量的直方图，并将其应用于数据库中的图像检索，其基本思想是：色彩更丰富（饱和程度更高）的像素在色调（H）直方图中获得的权重比色彩更少（饱和度更低）的像素高。通过计算S 分量加权H 分量的直方图，可以减小像素对标准色调（H）直方图的影响。然而，在实际的彩色图像分析中，仅对彩色图像的色调（H）分量进行大小为饱和度（S）自身的加权，往往不能得到易于分析的直方图，尤其在对图像进行分割处理时，直方图的好坏对最佳阈值选取尤为重要。为此，本文在HANBURY研究成果的基础上，引入可变的指数加权因子α，提出S 分量指数加权H 分量的直方图公式，该公式将H 分量直方图、S 分量加权H 分量的直方图作为特例。线性直方图上的Otsu 法和最大熵法是2 个经典的阈值分割方法［16-17］，本文提出圆形直方图上的最大熵法并给出递推公式［12-14］。LAI等［18］基于线性Otsu 法给出2 个圆形Otsu 版本，本文给出另一种圆形Otsu 法的表述，并以最优指数加权因子的饱和度指数加权色调直方图作为预处理，通过对圆形最大熵 法、LAI等［18］所提2 个圆形Otsu 版本进行对比 实验，以验证本文方法的有效性。

1 S 分量指数加权H 分量的直方图

传统的线性直方图通过统计像素点在整幅图像中出现的次数来反映一幅图像的像素分布，而圆形直方图不同于线性直方图，其直方图的起点和终点是相连接的，如图1 所示。相较RGB 颜色图像，HSI颜色图像更能匹配人眼的颜色感知，这在一些光照不均匀的情况下能够发挥优势，因此，许多研究人员在图像分割中使用HSI 颜色空间模型［5-6］。H 分量是颜色“质量”的反映，每种颜色都有相应的波长和色相。因为色调独立于高光和阴影，所以色调对于区分不同颜色的物体非常有效，充分利用彩色图像的色调分量信息，可以使图像分割达到期望结果。彩色图像的色调值是在[0°，360°)区间内周期性变化的，色调H 分量的频率直方图通过首尾连接而形成圆形直方图，因此，圆形直方图能够体现色调值呈周期性变化这一性质。

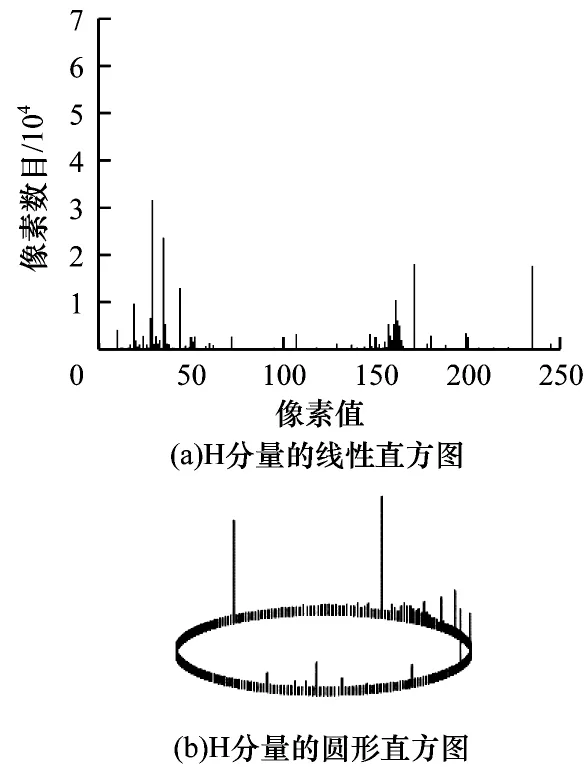
图1 H 分量直方图Fig.1 H-component histogram

本文用H(x，y)表示色调（H）分量通道尺寸为M×N的彩色图像中任意像素的色调（H）值，将H 分量在每一个色调θ上的出现频率记为h(θ)，表示式如下：

其中：θ∈[0°，…，360°)表示H 分量直方图的取值；δ表示kronecker 符号函数。

如前文所述，用H 分量直方图进行处理具有局限性，为此，HANBURY［15］提出通过S 分量加权H 分量直方图的方式来改善直方图，具体公式如下：

在HSI 颜色空间中，H 分量表示颜色种类，S 分量表示颜色的鲜艳程度。为了进一步增强H 分量的表示效果，本文通过引入指数加权因子α来增强或削弱饱和度（S）的影响。S 分量指数加权H 分量的直方图定义如下：

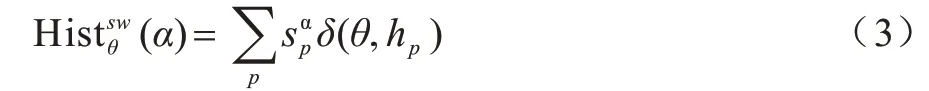
其中：指数加权因子α可以为任意非负值。

当指数加权因子α=0 时，式（3）仅表示原来的H 分量直方图（式（1））；当指数加权因子α=1 时，式（3）即为HANBURY［15］给出的表述（式（2））。可以看出，式（3）具有一般性。如何确定合适的α值，下文将在实验部分进行讨论。

2 圆形直方图上的阈值法

圆形直方图的阈值化方式不同于传统的线性直方图阈值化方式。线性直方图的2 类阈值只需要找到一个介于灰度直方图区域[0，1，…，N-1]内的阈值点，然后将线性直方图分成2 个部分，而圆形直方图的0 点和N-1 点首尾相连，2 类阈值需要找到2 个阈值点，然后将圆形直方图分成2 个部分。借鉴灰度直方图阈值中的Otsu 法，LAI等［18］给出圆形直方图上的2 种阈值选取准则。

对于圆形直方 图{h(t)}，t∈Ω=[0，1，…，N-1]，N-1 和0 这2 个元素相邻，需要找到2 个阈值t0和t1（沿逆时针方向寻找阈值，t0∈Ω，t0≺t1，“≺”代表逆时针方向），其中，第一个阈值作为圆形直方图的起点，另外一个阈值将圆形直方图分为2 个部分。参考LAI等［18］所给的定义，如果t0≤t1，则t0到t1的部分记为t0…t1；如果t0＞t1，则t0到t1的部分记为t0…N-1 ∪0…t1。将循环和定义为

t0…t1-1和t1…t0-1（逆时针方向）2 个部分的概率分别记为：

在线性直方图上，针对最大类间法的Otsu 有3 个等价描述［16，19］。LAI等［18］给出上述2 个阈值选取准则。作为对比，本文提出另一个阈值选取准则。圆形直方图的整体角均值的三角矩定义如下：

整体角均值μL定义为：

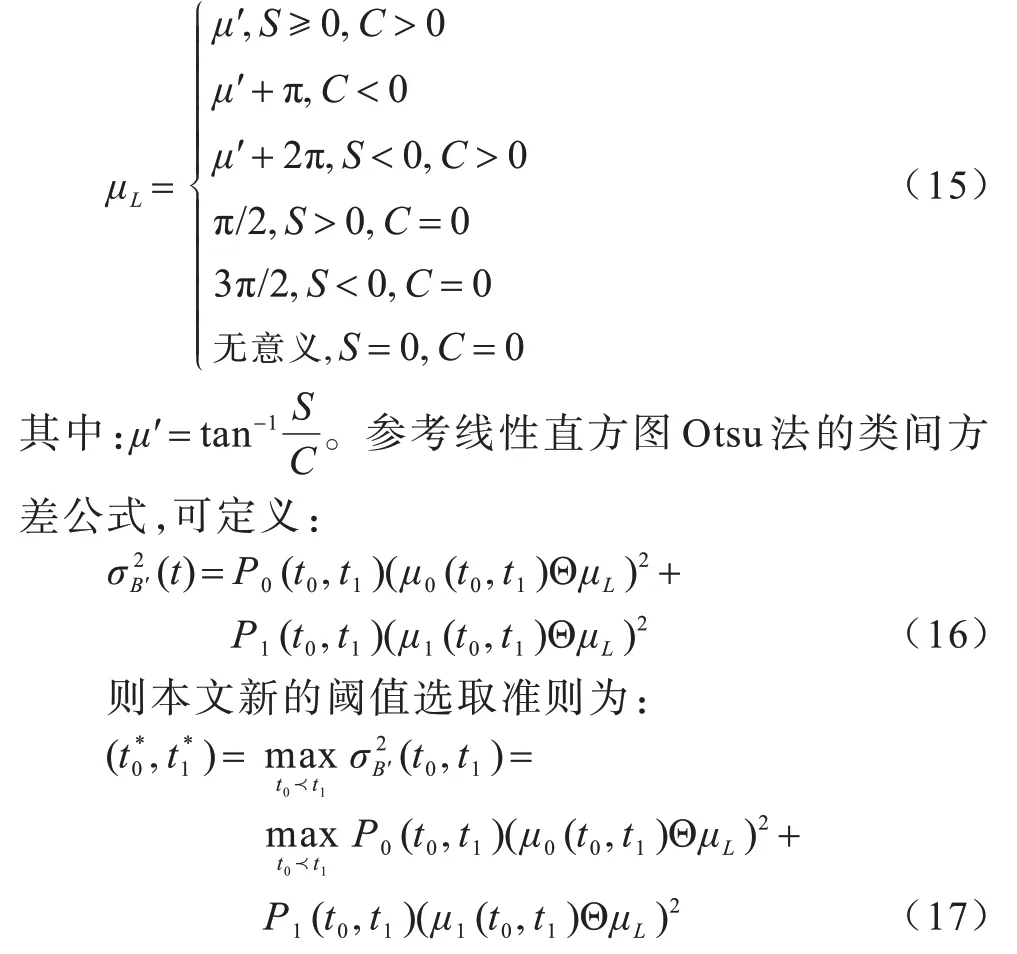
圆形统计［20-22］与线性统计存在差异，因此，与LAI等［18］的讨论结果相同，式（17）与式（10）、式（11）并不等价。

3 实验结果与分析

3.1 指数加权值确定

图2（a）是一幅实际采集的图片，图2（b）是图2（a）在HSI空间下的图像，图2（c）、图2（d）分别为图2（a）的色调（H）、饱和度（S）通道。在检查色调（H）图像时，可以看到，对于低饱和度（黑色或白色）区域，色调（H）可以有一个很大范围的取值，这并不对应于彩色图像中任何显著的颜色差异。简单的H 分量直方图只计算每个色调（H）值在色调通道中出现的次数，如图3（a）所示。这个直方图最值得注意的特性是存在等间距的尖峰，这些峰值是由于在离散网格上使用极坐标系统引入的离散误差所造成的，KENDER［23］首先指出了这一点，它们的高度在包含大量灰度像素的图像中被放大。S 分量指数加权H 分量的直方图如图3（b）～图3（d）所示，可以看出，峰值的振幅大幅减少，且随着加权因子α的不断增大，峰值振幅下降幅度也增大，从而得到一个更容易解释的直方图。

图2 车牌图Fig.2 License plate map

图3 图2（c）在不同指数α 加权后的直方图Fig.3 Fig.2（c）histogram after different index α weighting

本文提取了色调（H）图像中像素数目最多的色调值，图4中提取图2（a）在155～165范围内的H分量值，可以看到，这些峰值对应图像中饱和程度最高的区域颜色，但是，这些峰值在简单的H分量直方图上并不容易识别。通过结合H阈值和S阈值，可以很容易地去除由这些阈值提取的附加背景像素。图5显示利用圆形直方图上的最大熵法［12-14］对由不同指数加权因子得到的直方图进行阈值选取分割后的图像，可以看出，当加权因子α=2时，分割出的车牌相较其他加权因子值时效果更优。

图4 图2（a）在155～165 范围内的色调分量值Fig.4 Fig.2（a）H-component values between 155 and 165

图5 不同指数加权后的最大熵分割图Fig.5 Maximum entropy segmentation graph weighted by different indexes

图3（a）～图3（d）验证了利用S 分量对H 分量直方图进行加权处理后可以得到更平滑、更易于解释的直方图，有助于后续分割过程中对阈值进行选取。如何确定合适的加权因子值是应用的关键，为此，本文以1 为加权因子值的临界点，对大于1（实验中只取到5）和0～1 之间的不同加权因子值，以0.1 为步长进行测试，从而得到最合适的加权因子值。经过对Berkeley 等图像数据库中图片的大量测试后发现：在区间［0.1，0.8］范围内的饱和度加权色调直方图分割后的图像基本上没有变化，因此，不失一般性地，选取α=0.5 作为该区间范围内的代表值；在区间［0.9，1.8］范围内的饱和度加权色调直方图分割后的图像变化不大，因此，不失一般性地，选取α=1 作为该区间范围内的代表值；在区间［1.9，5.0］范围内的饱和度加权色调直方图分割后图像变化不大，因此，不失一般性地，选取α=2 作为该区间范围内的代表值。基于图5 实验以及对公开图像数据库的测试结果，本文最终将α=2 作为指数加权值。

3.2 圆形阈值法比较

为了测试本文所提方法的性能，在PC 机上用MATLAB（2018 版）在H 组件上进行实验。在实验之前，先对H 分量进行S 分量指数加权预处理，然后比较LAI等［18］给出的式（12）、式（13）和本文提出的新阈值准则式（17），此外，还使用文献［12-14］中不同的圆形最大熵阈值法作为对比。其中：文献［12］通过在圆形直方图中引入累积分布函数，然后利用累积分布函数的最优熵，沿顺时针或逆时针方向将圆形直方图扩展为线性直方图；文献［13］将洛伦兹曲线引入圆形直方图，通过洛伦兹曲线的最佳索引，将圆形直方图沿顺时针或逆时针方向扩展成线性直方图，最后通过对线性化圆形直方图采用熵阈值得到彩色图像的目标；文献［14］是在圆形直方图上直接进行阈值选取，提出一种基于圆形直方图的最大熵阈值递归方法，使得在2 类或多类阈值的圆形直方图上搜素最优阈值的运行时间大幅缩减，提高了分割效率。通过分析可以发现，本文所提方法与文献［12-13］方法的区别主要在于对H 分量直方图的预处理和最佳阈值的选取方式上，本文通过式（17）选取最佳阈值对，而文献［12-13］先选取最佳断点将圆形直方图线性化后再利用阈值准则选取最佳阈值；本文所提方法与文献［14］方法的主要区别在于对H 分量直方图的预处理以及圆上阈值对选取准则的不同，文献［14］主要针对圆上最大熵法的时间复杂度进行优化，而没有提升分割结果的其他评估指标。综上，本文方法的优势在于对H 分量直方图的预处理，以及利用圆形统计提高圆形直方图阈值选取的一般性和适用性。

图6 所示为Berkeley 图像数据库中的6 幅RGB原图，图7 所示为图6 对应的H 分量圆形直方图，图8所示为图6 对应的指数加权因子α=2 时的S 分量加权H 分量圆形直方图，图9 中从左到右分别为利用式（12）、式（13）、文献［12-14］中的圆形最大熵阈值法以及式（17）所得的2 类分割结果图，最后一列为基准分割结果。以基准分割图作为参考，通过对比可以看出，相较LAI等［18］给出的式（12）、式（13）以及圆形最大熵阈值法［12-14］，本文提出的圆上阈值分割准则分割结果更好，目标区域更加明显，与基准图更为相近。

图6 RGB 原图Fig.6 RGB original images

图7 图6 对应的H 分量圆形直方图Fig.7 H-component circular histograms of the fig.6

图8 图6 对应的S 分量加权H 分量圆形直方图Fig.8 S-component weighted H-component circular histograms of the fig.6

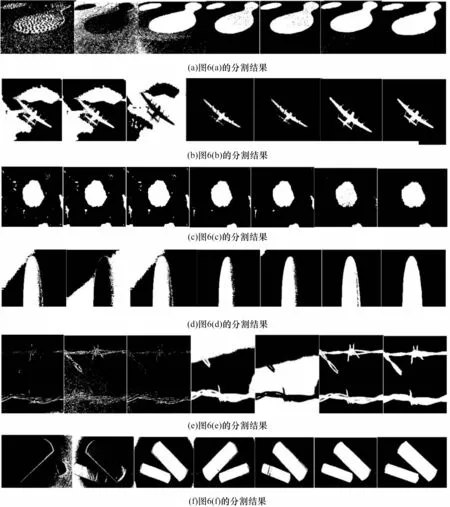
图9 不同方法的分割结果对比Fig.9 Comparison of segmentation results of different methods

为了定量比较不同阈值分割准则的分割性能，使用图像分割质量评价指标［24-25］对分割效果进行评估。表1所示为6种阈值化方法的所有分割结果的时间平均值（运行15次）、平均像素精度（PA）值［24］和平均结构相似度（SSIM）值［25］。从表1可以看出，相较LAI等［18］给出的式（12）、式（13）以及文献［12-14］中的圆形最大熵阈值法，本文提出的新的阈值分割准则具有最高的PA值和SSIM 值，更接近于基准图。对于PA 和SSIM 这2个指标，式（12）、式（13）可能存在分割色调值的问题，而本文方法可以修改式（12）、式（13）对色调的分割结果。

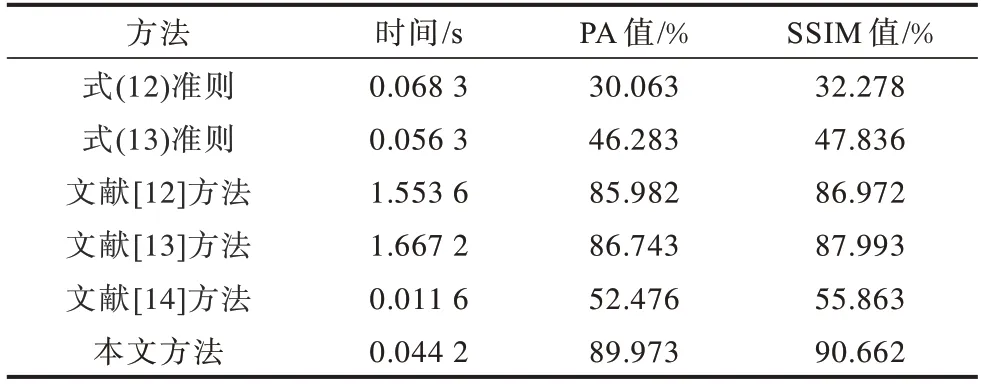
表1 6 种分割方法的性能对比结果Table 1 Performance comparison results of six segmentation methods

4 结束语

H 分量圆形直方图中存在较多毛刺，不利于阈值选取，为此，本文给出一种S 分量指数加权H 分量的直方图公式，并通过大量实验得出指数加权因子的最优取值，在此基础上，提出一种新的圆形直方图阈值分割法。该方法以S 分量指数加权H 分量的直方图作为预处理，将其与文献［12-14］所提圆形最大熵阈值分割法、文献［18］给出的2 个圆形直方图阈值分割准则进行实验对比，结果表明，本文圆形直方图阈值分割法具有有效性。下一步将在本文方法的基础上将2 类阈值扩展为多类阈值，以实现对多类复杂情景的目标分割。