基于神经网络算法的救生筏橡胶基布质量预测方法

刘智玉，刘佃森，汪 军

(1.上海游龙橡胶制品有限公司，上海 201205；2.东华大学 纺织学院，上海 201620)

1 救生筏质量要求

救生筏的生产加工过程较为复杂，在原料纱线、坯布性能、织物结构、橡胶性能、加工工艺和成品救生筏性能之间存在着内在的非线性关系。救生筏生产企业在产品生产过程中，普遍会在标准要求的基础上额外增加一些质量冗余量，以形成一个“质量安全区”，可以对冲产品质量波动带来的潜在风险；但 如果质量安全区预留范围过大，则意味着生产中需使用质量过剩的原料和更高的加工工艺，会显著增加生产成本；此外，由于目前增加救生筏产品牢固度和质量的主要手段是通过增加救生筏基布厚度和橡胶涂层厚度来实现，所以质量冗余量过大，会造成救生筏偏厚重，其轻量化受到影响。另外，在现实中有些生产企业为了降低成本，盲目追求轻量化而将质量安全区偏小掌握，在遭遇产品质量波动时，出现最终产品检测质量不达标的情况。近年我国曾对市面上出售的渔船气胀式救生筏进行集中质量抽样专项检查，检查范围涵盖全国11家气胀式救生筏生产企业，检查结果显示，救生筏合格率仅为85.7%[1]。

可见，如果想将救生筏的质量安全区控制在既能满足质量要求，又能满足产品的轻量化需求，并合理降低产品成本的范围，就需在科学研究指导下进行。

目前常见的研究方法是通过采购不同原料，修改加工工艺生产试验样品，然后对样品进行检测，以确定原料及加工工艺的质量安全区，但这种方法会浪费大量试验样品及人力、物力，且效率极低。因此，若能找到一种替代历史经验的虚拟产品质量预测方法，则能为合理确定质量安全区提供更高效准确的依据，从而提高企业生产效率和产品竞争力，达到产品标准规定和满足实际使用中对救生筏的质量要求，对救生筏企业具有重要的现实意义。

在机器学习技术出现之前，纺织领域主要应用数学和统计模型进行产品质量预测。随着机器学习技术的发展，逐渐在纤维分类、纱线纺制、织物疵点检测、印染质量预测等领域都得到应用[2-4]。但目前在救生筏产品领域还没有应用研究的相关报道。在众多机器学习技术中，人工神经网络(Artificial Neural Network，简称ANN)算法目前应用最为广泛。神经网络算法容错能力较好，具有自适应性，自学习能力较强，善于处理数据间的非线性关系。本文的研究重点是基于神经网络算法根据坯布质量进行救生筏橡胶基布质量预测的方法研究。

2 预测模型建立

2.1 特征参数选择

救生筏体的质量要求主要为：满足浮力、不漏气、抗损坏(抗气压压力、常见碰撞等)。救生筏体的橡胶基布质量是保障这些优异性能的关键点之一。我国水产行业标准规定，橡胶基布以5000 m或月产量为一批提交验收，其抗拉强度、撕裂强度等指标的抽样率为每批抽样1次[5-6]。在生产质量控制中，这种检测抽样率只适用于产品质量波动小且无异常状况发生的情形，如果产品质量异常波动，就存在无法发现次品的概率。由于抗拉强度、撕裂强度等指标的检测是破坏性试验，所以即使要控制因质量异常造成的次品率，也只能尽量合理地增大抽样率，无法将抽样率提升太高。此外，从坯布到橡胶基布的加工成本较高，若对橡胶基布加大抽样率，检测成本会较大。如果能通过对坯布质量的检测结果预测出橡胶基布的质量水平，则可通过加大对坯布检测抽样率代替增大橡胶基布抽样率，实现较低成本监测橡胶基布的质量。

根据标准质量要求及生产实践经验，选出对橡胶基布质量影响较大的坯布经向抗拉强度、坯布纬向抗拉强度、坯布经向扯断伸长率及坯布纬向扯断伸长率这4项质量指标作为神经网络的输入变量，并以橡胶基布的经向抗拉强度、纬向抗拉强度、经向撕裂强度、纬向撕裂强度这4项质量指标作为输出变量，建立橡胶基布质量预测模型。

2.2 神经网络设计

1989年Robert Hecht-Nielsen证明了多层感知器(MLP)的万能逼近定理(Universal Approximation Theorem)，即对于任何闭区间内的1个连续函数f，都可用含有1个隐含层的神经网络来逼近[7]，因此1个3层的神经网络能完成任意m维到n维的映射。一般普通数据集常用单隐层的3层神经网络来进行质量预测建模。笔者也采用这种架构，建立了1个包含单隐层的3层MLP神经网络模型。

神经网络最重要的参数之一是隐层中神经元节点的个数，选择神经网络中隐层神经元节点数的经验公式[8-9]为：

(1)

式中：

s——隐层神经元数；

m——输入神经元数；

n——输出神经元数。

以m，n为4，代入式(1)，计算得s值为5.2。采用样本数据多次试验，最终选定网络的隐层神经元数为5，建成的3层神经网络预测模型为4-5-4结构，如图1所示。

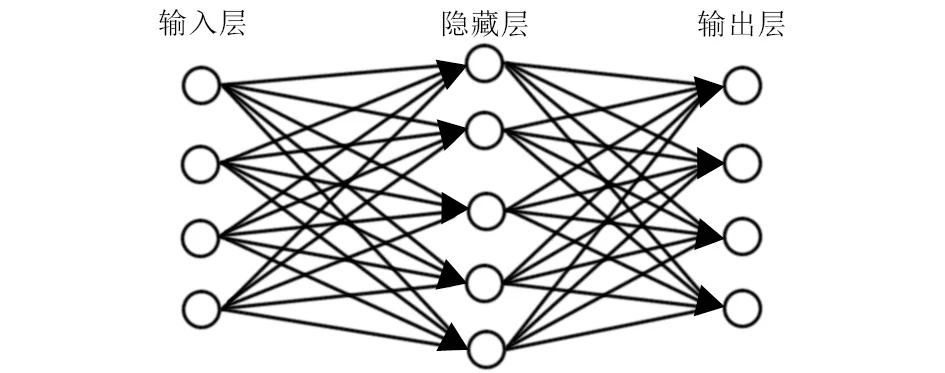
图1 3层神经网络预测模型

使用不同超参数值运用该预测模型进行预测，经过对比试验确定优选的超参数设置，最终确定该神经网络的主要超参数设定：优化器为均方差传播算法RMSprop，迭代轮次为1000，学习率为0.001，激活函数选择ReLU函数。本模型的编程语言为Python，深度学习框架为Keras。

3 试验方法

本试验共有42个样本数据，其中，将28个样本数据作为训练集，7个样本数据作为验证集，7个样本数据作为测试集。在应用神经网络时，所有输入特征的变化范围越相似，则预测效果越好。当所有输入特征的均值为0、方差为1时是最理想状态，对试验数据采用标准化处理方法[10]进行数据缩放，可以达到这种效果。本试验在预测前对所有样本数据均进行了标准化处理。

预测后将预测值与实测值对比，并采用平均绝对百分比误差(MAPE)作为评估指标。其表达式为：

(2)

式中：

p——测试集样本数；

yi——第i个测试样本的实测值。

4 试验结果分析

橡胶基布经向抗拉强度、纬向抗拉强度、经向撕裂强度、纬向撕裂强度的实测值与预测值比较分别见表1～表4。

表1 经向抗拉强度的实测值与预测值比较

由表1～表4可知，橡胶基布经向抗拉强度、纬向抗拉强度、经向撕裂强度、纬向撕裂强度这4项质量指标的预测值相对于样本实测值的平均绝对百分比误差(MAPE)分别为1.15%，0.53%，0.69%，0.68%。在所有预测值中，单值最高绝对百分比误差为2.40%，这充分表明该神经网络预测模型是有效的。

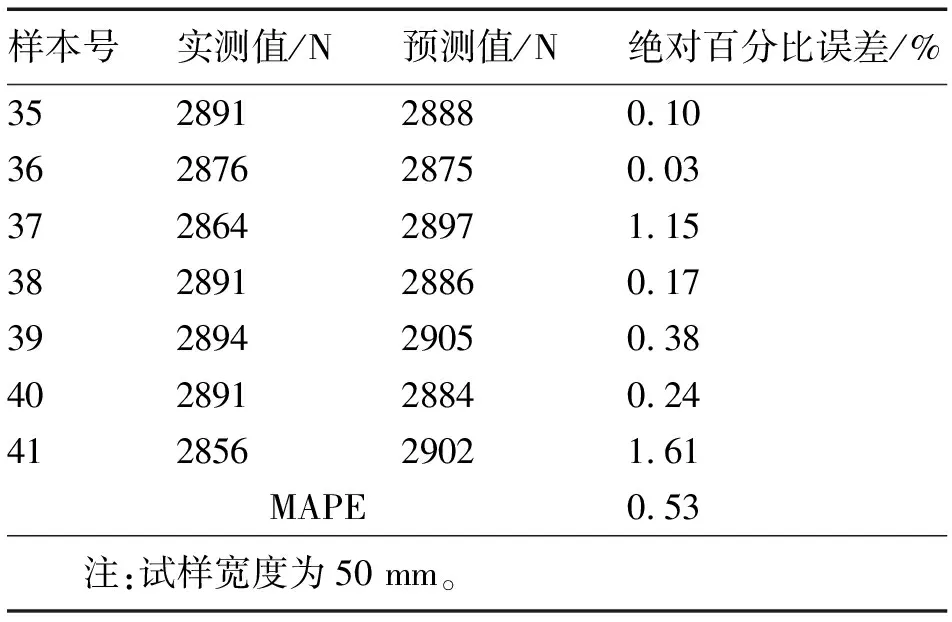
表2 纬向抗拉强度的实测值与预测值比较

表3 经向撕裂强度的实测值与预测值比较

表4 纬向撕裂强度的实测值与预测值比较

在实际生产质量控制中，不同质量指标的质量安全范围常控制为15%～30%，因此该神经网络预测模型的准确度可满足生产实践中对质量安全区优化控制的要求。

5 结语

笔者研究建立了救生筏橡胶基布质量预测的神经网络模型。根据救生筏产品质量标准，对救生筏功能及质量具有重要影响的橡胶基布抗拉强度和撕裂强度进行质量预测。将橡胶基布的坯布抗拉强度和扯断伸长率作为输入变量，采用MLP神经网络建立橡胶基布质量预测模型。经试验得知，预测值与实测值吻合较好，橡胶基布经向抗拉强度、纬向抗拉强度、经向撕裂强度及纬向撕裂强度4个质量指标的预测值相对于样本实测值的平均绝对百分比误差分别为1.15%，0.53%，0.69%，0.68%，预测值与实测值的绝对百分比误差均远小于生产实践中质量安全区常见控制范围。运用该质量预测模型，在满足质量安全区控制要求的同时，提高了预测速度且减少了成本浪费。