基于振动信号的热辊运行监测方法
刘冠华,薛 学,王 青,彭森林,袁明清,侯 伟
(1.北京中纺精业机电设备有限公司;2.中国纺织科学研究院有限公司:北京 100016)
0 引言
热(冷)牵伸辊在化纤生产过程中对原丝起加热和拉伸作用,能够使纤维达到生产所需的力学特性和物理特性,是化纤生产机械的核心部件之一[1]。热辊轴承长期在高温高速状态下运行,相对于一般旋转机械的轴承更易损坏。对热辊的运行状态进行监测,特别是对热辊轴承寿命状况和受损状况进行监测,有助于降低设备维护成本,保证设备安全稳定运行,避免因轴承故障造成经济损失[2-3]。
旋转机械的轴承检测诊断方法,比较常见的有模式识别法、人工神经网络和仿生模式识别[4-6]。模式识别法是通过获取机械运行时的振动、温度和应力应变等信号,对信号进行相关分析得到机械的运行状态。其中通过振动信号对机械运行状态进行分析能够占到总分析方式的70%[7]。Aurelien等采用时频转换法对电机运行时轴承受到电流影响后产生的振动进行分析,结果显示通过T-F方法进行振动分析可以有效检测轴承的损坏状况,并且能够避免直接采用傅氏变换后信号中包含部分错误信号给分析带来误差的弊端[8]。陈东超等提出了一种基于广义回归神经网络模型的旋转机械振动特征预测策略,并应用于实际核电机组的振动特征预测,结果表明新网络模型的总体性能优异,在学习样本较少的情况下也能得到较为满意的预测结果[9]。郭玉将仿生模式识别算法应用于旋转机械故障诊断中,其试验结果表明仿生神经网络在一定程度上优于BP神经网络和 RBF 神经网络,说明仿生模式识别在旋转机械故障诊断中是一种可行且高效的诊断方法[10]。
考虑到热辊的工作环境较差、连续工作时间较长,同时监控的热辊数量较多的现状,下文优先采用模式识别法进行诊断,目的是能够简单、高效地实现热辊的检测和诊断。采用模式识别法还能将相关特征进行储存,方便专业技术人员在设备维护时查验。
1 振动检测和计算方法
1.1 振动检测
对热辊进行诊断,首先需要对热辊进行检测以获取设备运行时的相关数据。将振动传感器在出厂时预设好休眠时间和工作时间,使传感器定期采集热辊的振动信号并传输给上位机进行计算分析,具体流程如图1所示。振动信号传输到上位机后,由上位机的控制程序对信号进行处理。当处理结果显示热辊运行状态良好时,仅将结果进行储存;当计算结果显示热辊运行状态存在问题时,会通过上位机向用户发出提醒或警告。一般来讲,热辊运行状态可通过热辊振动信号中的主要振动频率和对应频率下的振动加速度幅值反映出来,因此需要对热辊的振动信号进行处理。

1—热辊;2—振动传感器;3—数据采集卡;4—上位机;5—振动分析结果。
1.2 振动计算方法
针对热辊的振动信号,可采用随机子空间识别方法(Data-SSI)进行参数识别。随机子空间识别方法抗噪能力良好,适用于密集模态识别。将运行的热辊看做具有N个自由度的系统,其振动响应可用二阶线性微分方程描述:
Mq″(t)+Cq′(t)+Kq(t)=f(t)
(1)

(2)
式(2)中,x(t)为系统的状态向量,x′(t)为系统状态向量的一阶导数。B2为激励力位置输入矩阵,u(t)为输入向量,设r为振动输入的激励点数,则输入向量应为r×1阶。I为单位矩阵。设初始时间为t0,则对变换后的式(1)进行求解可得:

(3)
式(3)中,Ac代表着式(2)中x(t)前的矩阵,表示为系统矩阵;Bc则为u(t)前的矩阵,u(τ)为输出向量的卷积表达式,τ为卷积变量。但实际采集的振动信号均为离散的数据点,因此需将式(3)进行离散化,并令:
A=eAcΔt
(4)
式(4)中,A包含系统矩阵和时间变量,即表示为系统的状态空间。通过对系统状态空间A的计算,即可得到系统的实际运行特性。为了计算状态空间,需将实际采集的数据点直接输出组成Hankel矩阵,Hankel矩阵的构造方法如下:
(5)
式(5)中,yk为k时刻下各测试通道输出的数据,k=0,1,2,…,2i+j-2。因此,最终构件的Hankel矩阵为2i行j列的矩阵,且i的取值应尽可能远大于被测试系统的振动阶次。对Hankel矩阵进行QR分解以缩减数据量,并计算出投影矩阵O:
(6)
(7)
式(6)中,Yp表示历史矩阵,Yf表示未来矩阵。对投影矩阵进行奇异值分解:
(8)
U1为左奇异向量矩阵,V1为右奇异向量矩阵,S1为奇异值矩阵。得到系统的状态空间矩阵A:
(9)
式(9)中,Λ为对角阵,Λ=diag(λi),λi为离散时间系统的复特征值;Ψ为离散时间系统的特征向量矩阵。根据λi和Ψ的计算结果,从中提取振动频率的振动加速度幅值信息进行储存。不同频率的振动可相互叠加,当不同振动波的相位差为0时,叠加后的振动加速度幅值最大。预设最大振动报警阈值,当各频率振动加速度幅值之和大于报警阈值时,即会报警。
2 试验结果及分析
2.1 振动试验结果
从某公司生产的一批未完成整机平衡的热辊中随机抽样,抽样数为3。将3台样本热辊分别编号为1号、2号和3号,图2为热辊振动试验图。将所抽样本放置在整机动平衡仪上,变频器设置为140 Hz(热辊实际转速为8400 r/min),在热辊高速旋转条件下采用加速度传感器(Miro Detectors,Italian Sensors Technology)进行数据采集,并采用1.2小节所述方法进行计算。

图2 热辊振动试验
实际计算结果显示,存在数值接近的振动频率,这是由于计算结果存在一定误差导致。为避免结果重复,将计算结果中频率间隔小于±2 Hz的频率合并,振动加速度幅值取其各合并频率中的最大值。为了验证计算结果的准确性,将原始数据进行傅里叶变换,并通过人工操作,选取计算结果频率对应的振动加速度幅值进行对比,原始数据傅里叶变换如图3所示,对比结果见表1。

表1 热辊振动检测结果及计算误差对比
从振动频率的识别结果来看,振动频谱中振动加速度幅值最大的频率均能够通过计算得到。所有试验热辊振动最大频率约为143 Hz,这是由于在进行振动试验时采用的变频器激励为140 Hz,即热辊的工况为140 Hz。而实际采集与计算得到的热辊工作频率与变频器设定值存在差异,这可能是由于电机转速存在误差。1号与2号热辊接近29.5 Hz的振动比较大,通过1.2小节中计算方法可将其计算出来。从图3中3号热辊径向振动频谱图可以看出,除了143 Hz外还有很多小的波峰,这说明3号热辊的振动情况较为复杂。采用相同的计算方法对3号热辊进行计算时的频率计算精度比1号和2号差,但依旧能够通过计算得到部分主要的振动频率。

a) 1号 b) 2号 c) 3号
从振动加速度幅值计算结果看,1号和2号热辊在29.5 Hz和143 Hz处的振动加速度幅值计算相对误差均在10%以内。3号热辊在143 Hz处的计算误差为16.7%,是3个试验对象中最大的误差值,这可能与3号辊振动状况较复杂有关。3号热辊除143 Hz外,还存在一些振动加速度幅值偏大的频率,如68.7 Hz,84.6 Hz和113.9 Hz,该3处频率的计算结果最大误差为34.2%,出现在68.7 Hz处。整体看,1.2小节计算方法能够较好得识别出实际振动加速度幅值偏大的频率,但在计算个别试验对象的振动加速度幅值时误差偏大,且在计算低频振动加速度幅值时的误差也偏大,但低频振动在实际工况下振动贡献小,因此该误差在实际判断热辊振动时可忽略。
采用随机子空间方法进行计算时,计算结果也会受计算阶数的影响。在已定阶数内如果计算结果不能稳定,则会影响计算精度。同时,随机子空间方法虽然能够计算多个振动频率及其振动加速度幅值,但相邻两频率过近时,依旧会存在计算误差。根据以往试验经验,在频率范围为0~200 Hz时,热辊的振动频率数量较少,因此预定采用最高12阶进行计算。为了确定12阶计算结果是否稳定,将计算结果由低阶到高阶进行展示,并将计算稳定的结果在图中进行连接,结果如图4所示。
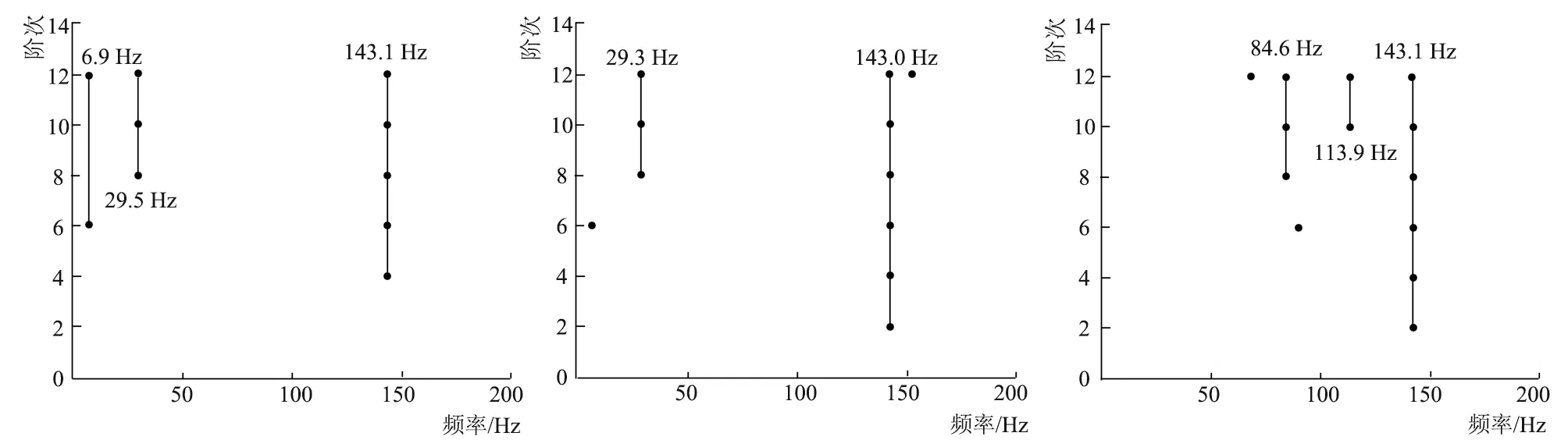
a) 1号热辊 b) 2号热辊 c) 3号热辊
由图4可知,主要振动频率均出现在第8阶处,至少连续出现2~3阶。通过多阶计算结果对比,将稳定出现的结果筛选出来作为最终计算结果。将表 1中非稳定计算结果去除后可知,稳定计算结果最大误差为28.1%,平均误差为10%。总体上说,由于热辊在0~200 Hz的振动峰较少,采用最高12阶进行计算能够满足实际应用要求。
试验结果显示,采用随机子空间法能够获取热辊不同频率的振动分量以及相应的振动加速度幅值。通过多阶频率计算结果,能够进一步去除非稳定频率,有助于提高频率计算精度和振动加速度幅值计算精度,提高频率计算结果的稳定性。这说明该方法在计算振动加速度幅值时的鲁棒性偏差,对振动加速度幅值的计算有进一步优化的空间。
2.2 振动诊断结果
为了使振动计算方法能进一步适用热辊的振动检测,并将结果应用于热辊运行状态报警,根据试验结果将计算振动加速度幅值取为实际计算值的130%。采用放大计算值的方法,给实际热辊的轴承状态留出足够的安全运行余量,以弥补计算结果带来的误差。
将各试验热辊的计算幅值按照:
(10)
式(10)中,S为试验热辊的最大振动速度幅值,fi为振动频率,Sfi为fi对应的计算振动速度幅值。根据ISO 10816《机械振动 通过非旋转部件的测量评定机械振动》可知,旋转机械的安全振动范围与机械的尺寸有关;对于中小型旋转机械,其提出的安全运转振动速度幅值应不超过2.3 mm/s,超过该振动速度幅值不利于旋转机械的长期运转。则热辊的振动可采用以下判断方式:
(11)
根据式(11)对热辊进行验证可知,3台试验热辊振动速度幅值分别为3.5 mm/s,3.0 mm/s和2.2 mm/s,判断结果为2台处于不稳定状态,1台处于稳定状态。由于实际上热辊未做整机平衡,整体振动速度幅值偏大,所以对热辊的振动检测是有效的。
3 结论
3.1随机子空间法能够比较准确地计算出热辊总体振动中各振动分量的频率。3个试验样本的主要振动频率143 Hz均能通过计算得到,1号和2号试验样本的次要振动频率29.5 Hz也能够通过计算得到,3号样本的振动分量较多时计算精度有所下降。采用12阶计算频率能够满足计算需要,但为了获得更准确的计算结论需将多阶计算结果进行对比,最终获取稳定的振动频率结果。
3.2将计算振动加速度幅值与傅里叶变换后的频谱加速度幅值进行对比得知,两阶振动频率接近时,振动加速度幅值计算结果会存在较大误差,且当振动成分比较复杂时,振动加速度幅值的计算精度有所下降。稳定频率的振动加速度幅值计算结果的最大相对误差为28.1%。
3.3将计算振动加速度幅值取为实际计算值的130%,采用放大计算值的方法,给实际热辊的轴承状态留出足够的安全运行余量,以弥补计算结果带来的误差。对改进后的样本振幅计算结果采用ISO 10816《机械振动 通过非旋转部件的测量评定机械振动》进行判断后可知部分样本振动偏大,符合试验样本未做整机平衡的情况,说明热辊的振动监测方法有效。

