25MnSiV矩形连铸坯温度场模拟研究
李海强,赵雷,徐晓林,王福星,李胜利
(1.鞍钢铸钢有限公司,辽宁 鞍山 114021;2.辽宁科技大学材料与冶金学院,辽宁 鞍山 114051)
连铸坯中心疏松缩孔对铸坯及最终产品的性能有重要的影响,疏松缩孔会降低钢的抗疲劳强度和抗拉强度[1-3],避免发生在凝固过程中的枝晶“搭桥”,能有效减轻疏松缩孔的程度[4-5]。 基于此,国内外冶金工作者做了大量深入细致的研究,P.Sivesson[6]认为,在铸坯中心部位固相率 fs=0.2 以下区域,钢液无法对铸坯中心产生的体积收缩进行有效补充几率增大而产生缩孔。G.T.Jeon等[7]分析了A356合金在铸造过程中的缩孔体积与钢液温度、模具温度和Sr含量的函数关系。在国内的研究中,颜慧成等[8]对连铸凝固过程进行传热分析,结果表明,拉速对凝固液芯长度的影响远大于过热度。陈亚楠等[9]针对连铸小方坯的中心疏松等质量缺陷建立了凝固传热数学模型,研究二冷强度对连铸小方坯凝固过程的影响规律,优化了二冷制度。但就国内外研究情况来看,针对铸坯表面温度和中心温度对其中心疏松缩孔的研究相对较少,并且这些研究中均未找出连铸过程中各工艺参数对铸坯表面温度和中心温度进而对疏松缩孔的影响规律,以及如何调整各工艺参数来确定最佳的连铸工艺。因此,本文以160 mm×220 mm矩形坯为研究对象,建立连铸数学模型,研究拉速、过热度、二冷区给水量对连铸坯表面温度和中心温度的影响规律,据此优化连铸生产工艺参数,降低铸坯疏松缩孔,指导现场生产实践。
1 数学模型的建立
1.1 几何模型建立与网格划分
采用切片法对连铸过程进行模拟,通过SolidWorks软件建立三维几何模型。为得到准确的计算结果并保证计算速度,网格元素尺寸设置为5 mm,总网格数超过442 714个,能够满足计算要求。数值模拟几何模型、网格结构三视图见图1。
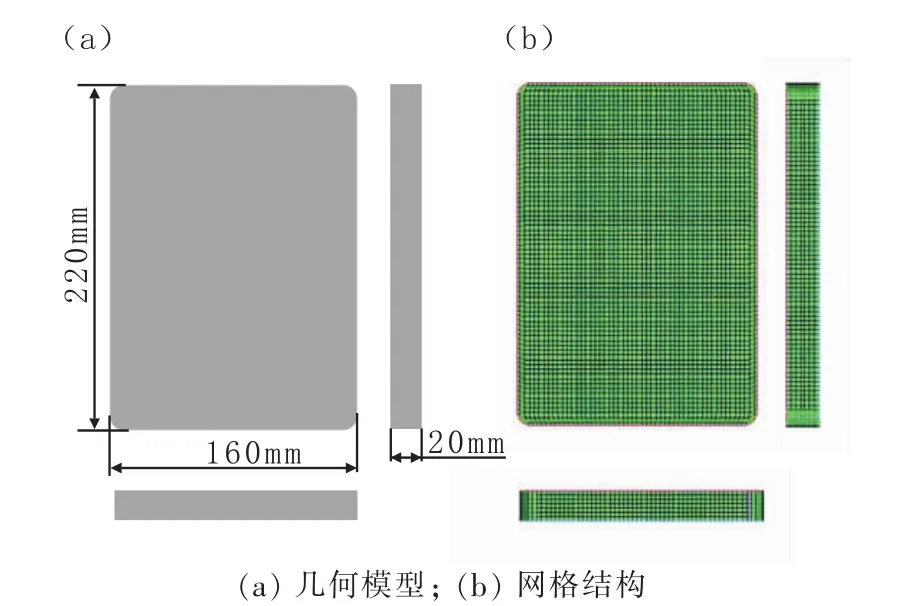
图1 数值模拟几何模型、网格结构三视图Fig.1 Orthographic Views for Geometric Model of Numerical Simulation and Lattice Construction
1.2 材料的物性参数
材料的热物理特性随时间的改变而改变,因此数值模拟过程中需要掌握材料在具体时刻的具体物性来定义边界条件。表1为25MnSiV钢化学成分。
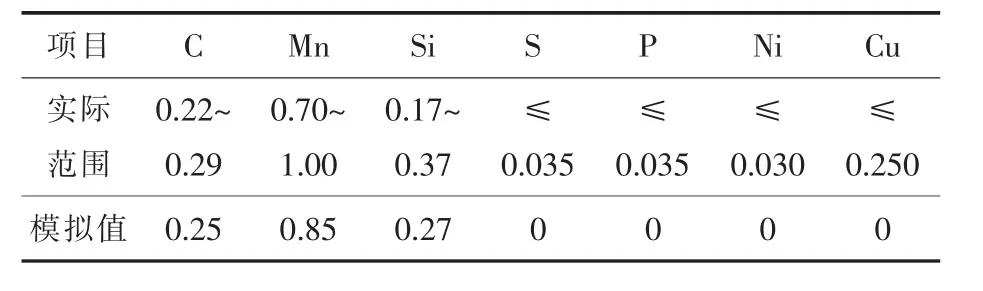
表1 25MnSiV钢化学成分(质量分数)Tab1e 1 Chemical Compositions in 25MnSiV Steel(Mass Fraction) %
液相线[10]和固相线温度计算公式[11]如下:
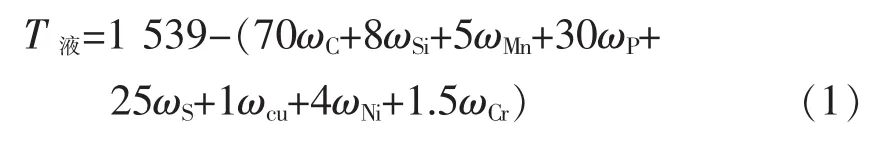
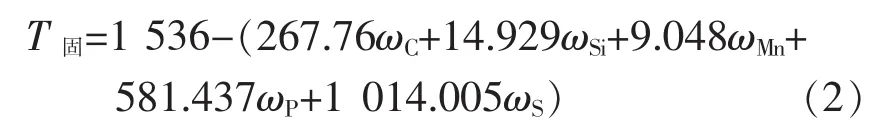
根据上式计算,得到25MnSiV的液相线温度为1 515℃,固相线温度为1 457℃。
1.3 初始条件和边界条件
钢水进入结晶器的时刻作为初始时刻,温度初始条件为浇注温度。数学模型建立的前提条件如下:
(1)用切片法进行模拟,假定铸坯任一横截面的上下部分绝热,即忽略拉坯方向的传热,模型简化为二维非稳态传热;
(2)钢液考虑为牛顿粘性不可压缩流体,凝固过程体积不变;
(3)钢种液相线和固相线不变;
(4)铸坯的物性参数视为各向同性。
由此,建立二维非稳态传热模型[12]如下:
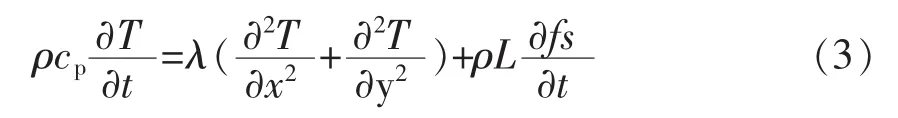
式中,ρ为密度,kg/m3;cp为比热,J/(kg·K-1);t为钢水在结晶器内的停留时间,s;λ为导热系数,W/(m·K-1);L 为熔化潜热,J/kg; fs为固相率。
结晶器内的传热可以用第二类边界条件来描述,结晶器内瞬时热流密度[13]为:

式中,q为结晶器内某一位置处钢液的瞬时热流密度,MW/m2;N为常数,由实际测定的结晶器热平衡与结晶器平均热流密度计算得出。结晶器瞬时热流密度与结晶器内平均热流密度的关系表达如下[14]:


式中,ρw为冷却水密度,kg/m3;cw为冷却水比热容,J/(kg·K-1);W 为冷却水量,m3/s;T1为结晶器出水温度,K;T2为结晶器进水温度,K;S为结晶器与钢液的有效接触面积,m2。
二冷区传热通常采用第三类边界条件描述,足辊区换热系数[16]可以表示为:
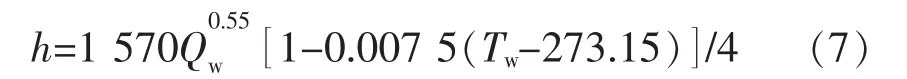
式中,h 表示足辊区换热系数,W/(m2·K-1);Qw表示二冷区冷却水流量,kg/s;Tw表示二冷区冷却水温度,K。其他二冷区换热系数可用下式[17]表示:

空冷区部分边界条件用辐射换热和对流换热描述,其热流密度可以表示为:
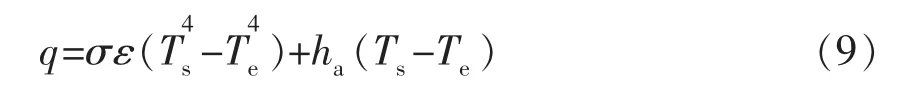
式中,σ 为玻尔兹曼常数,通常取5.669×10-8W/(m·2K4);ε为铸坯表面平均黑度,通常取0.8;Ts表示坯壳表层温度,℃;Te表示环境温度,℃;ha表示空气自然对流换热系数,通常为 5~25 W/(m2·K)。
1.4 数学模型的验证
对现场铸坯测温来验证本文模型的准确性。连铸工艺参数为:拉速1.11 m/min、浇铸温度1 530℃、结晶器水流量159.7 m3/h、结晶器水温差7.5℃、二冷足辊水流量3.4 m3/h、二冷一段水流量2.6 m3/h、二冷二段水流量1.9 m3/h、二冷三段水流量0.5 m3/h、二冷水总管温度27.3℃,测温位置分别在矫正轨之前和火焰切割前铸坯侧表面。实际测温与模拟温度对比见图2。每个点测温两次取平均值,测温点1测得温度值926℃,模拟结果测温点1温度值950℃,相对误差为2.59%;测温点2测得温度值781℃,模拟结果测温点2温度值为783℃,相对误差为0.25%。两个点实际值与模拟值相对误差均小于5%,可以认为该模型能很好地反映实际连铸过程。
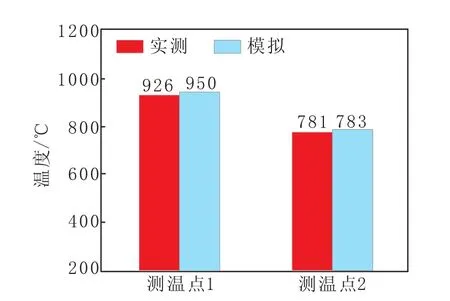
图2 实际测温与模拟温度的对比Fig.2 Comparison of Measured Temperature and Simulated Temperature
2 连铸坯凝固传热模拟结果分析
研究模拟拉速、过热度及二冷区给水量占比对铸坯温度的影响,结晶器及二冷区水流量具体参数设置见表2。

表2 结晶器及二冷区水流量具体参数设置Table 2 Special Parameters for Mould and Quantity of Water Supply in Secondary Cooling Zone
2.1 拉速对铸坯温度的影响
模拟拉速分别为1.0、1.2、1.4和1.6 m/min,过热度20℃(浇注温度1 535℃),二冷区最大给水量情况下,研究铸坯表面和中心温度变化规律,进而根据温度对铸坯疏松缩孔的影响机理确定最优拉速。图3为不同拉速下凝固末端铸坯横截面温度场分布。
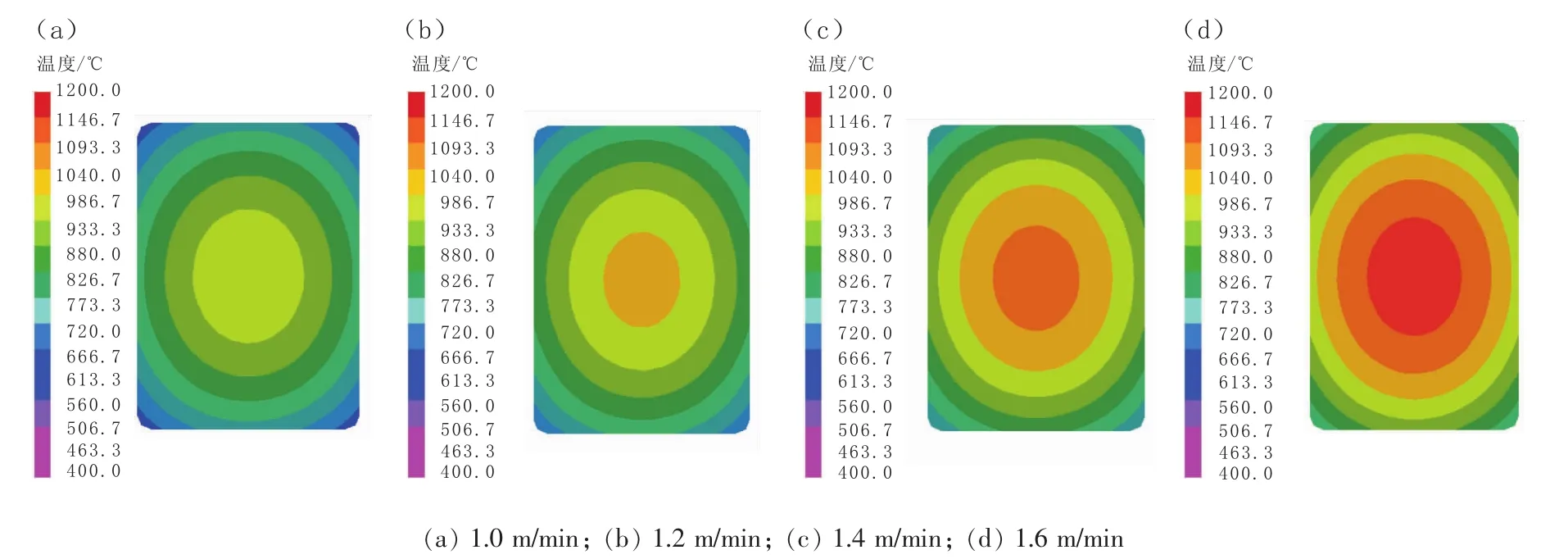
图3 不同拉速下凝固末端铸坯横截面温度场分布Fig.3 Temperature Field Distribution in Cross Section of Blank at Solidifying End-point under Different Casting Speeds
从图3中可以看出,拉速分别为1.0、1.2、1.4及1.6 m/min时,凝固末端铸坯横截面中心区域温度范围分别为 933.3~986.7 ℃、986.7~1 040.0 ℃、1 040.0~1 093.3℃及1 093.3~1 146.7℃。随着拉速的提高,凝固末端铸坯横截面中心温度逐渐增大,可以推断出铸坯液芯的长度逐渐增大,不利于钢液的补缩,因此可判断出铸坯疏松缩孔会逐渐增大。
图4为不同拉速下铸坯表面温度和中心温度随距弯月面距离的变化情况。
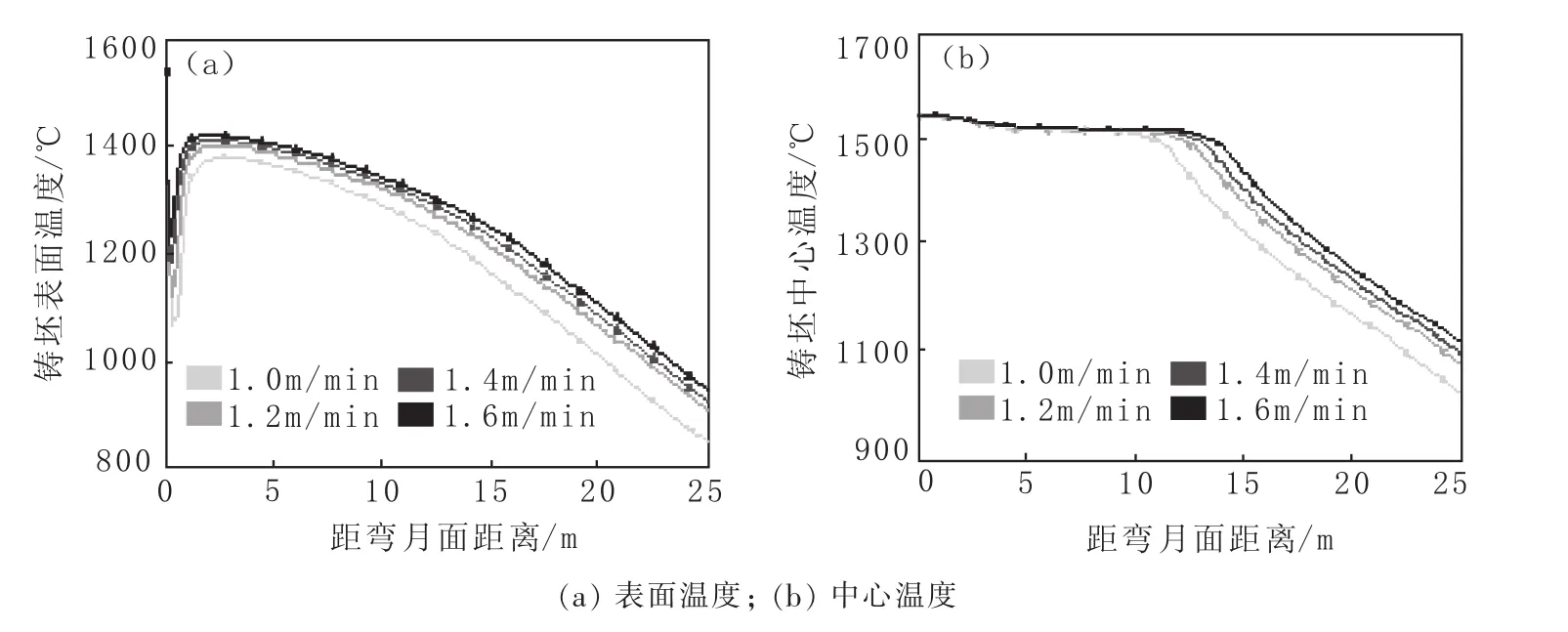
图4 不同拉速下铸坯表面温度和中心温度随距弯月面距离变化情况Fig.4 Changes of Surface Temperature and Center Temperature in Terms of Blank with Distance Changing from Meniscus under Different Casting Speeds
从图4(a)可以看出,由于结晶器内冷却强度较大,铸坯表面温度迅速下降到1 200℃以下,拉速越小,铸坯出结晶器的温度越低。拉速1.0 m/min时,铸坯表面在出结晶器时温度大约为1 050℃;拉速1.6 m/min时,大约为1 200℃,可见在结晶器内不同拉速对于铸坯表面温度的影响较大。
铸坯出结晶器后,由于冷却强度突然降低,导致铸坯表面温度出现了巨大的回升,过大的回温会导致凝固前沿拉应力的产生进而产生内部裂纹。从图4(a)看出,铸坯最大回温点出现在距弯月面距离2.5 m处,即二冷一段末端。拉速分别为1.0、1.2、1.4和1.6 m/min时,铸坯表面回温分别为325、275、240和201℃。因此可以推断,拉速越低,铸坯在出结晶器时回温现象越明显。二冷一段末端之后铸坯表面温度逐步下降,没有出现回温现象,且拉速对于铸坯表面温度的变化影响不大。从图4(b)可以看出,由于铸坯中心钢液潜热的释放,中心温度在很长一段时间保持不变。随着拉速的提高,铸坯中心温度下降的位置有所延后,拉速为1.0 m/min时,铸坯中心温度在距弯月面距离10 m处之后明显下降;拉速为1.6 m/min时,在距离15 m处之后明显下降。另外可以明显看出,在凝固末端拉速越大,铸坯中心位置温度越高,拉速1.6 m/min比拉速1.0 m/min凝固末端铸坯中心温度高100℃左右,这与前面凝固末端温度场的分布情况吻合,温度高,液芯长度大,不利于补缩的进行。
2.2 过热度对铸坯温度的影响
模拟过热度分别为 20、30、40和 50℃(浇注温度分别为 1 535、1 545、1 555、1 565 ℃), 拉速为1.0 m/min,二冷区给水量为最大给水量情况下研究铸坯表面温度和中心温度变化规律,进而确定最佳过热度。图5为不同过热度下凝固末端铸坯横截面温度场分布。从图5中可以看出,过热度在20~40℃之间变化时,铸坯中心温度位于同一温度梯度,即666.7~720.0℃。过热度从40℃增加到50℃过程中,铸坯中心温度升高一个温度梯度,大约60℃左右,这显著拉长了铸坯液芯长度,导致补缩困难,产生缩孔,这可以很好的说明疏松缩孔的产生与钢水的温度分布密切相关。
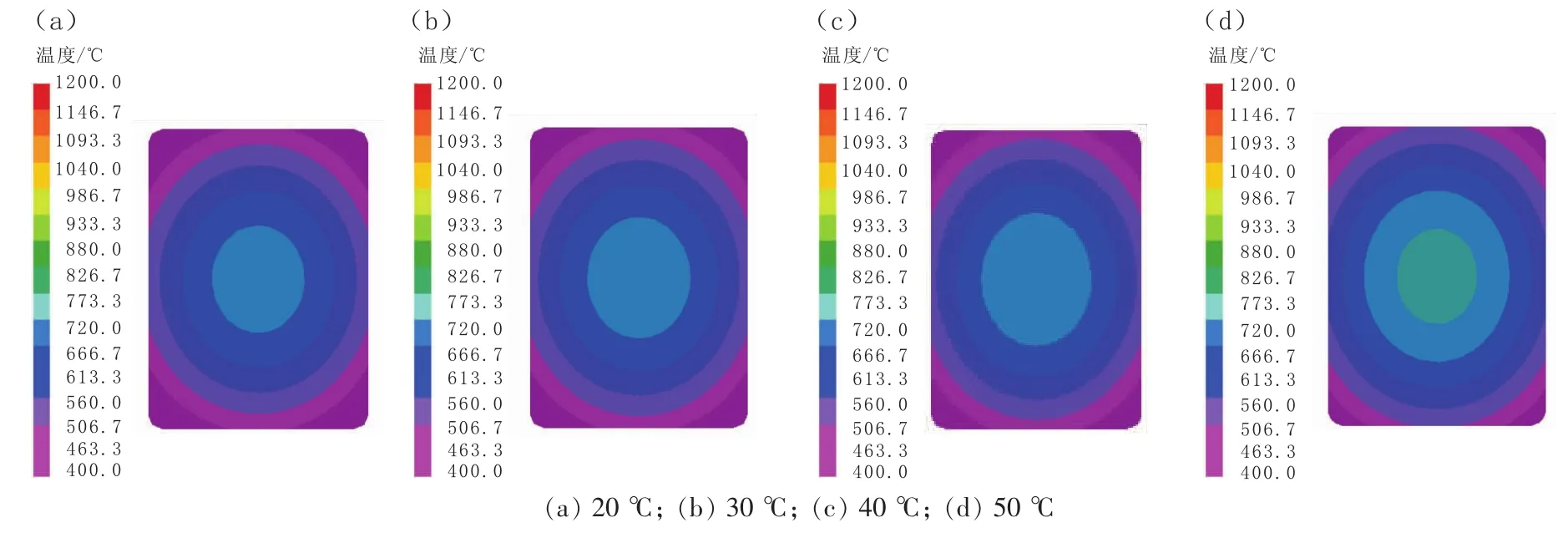
图5 不同过热度下凝固末端铸坯横截面温度场分布Fig.5 Temperature Field Distribution in Cross Section of Blank at Solidifying End-point under Different Degrees of Superheat
图6为不同过热度下铸坯表面温度和中心温度随距弯月面距离变化情况。从图6(a)看出,过热度在20~50℃变化过程中,铸坯表面温度随距弯月面距离变化趋势一致,且过热度对于连铸过程中铸坯表面温度影响不大。铸坯出结晶器时,由于结晶器的强冷作用,铸坯表面温度迅速降低到1 250℃,不随过热度的变化而改变。铸坯出结晶器后进入二冷区迅速发生回温现象,之后随着连铸过程的进行,铸坯表面温度以相同趋势逐渐下降,整个过程中,相邻过热度铸坯表面温度始终相差20℃左右。由图6(b)看出,铸坯中心温度下降的位置都出现在距弯月面距离大约12 m处,不因过热度的不同而发生改变。在整个连铸过程中,过热度对于铸坯中心温度的变化影响不大,铸坯中心温度基本相同。
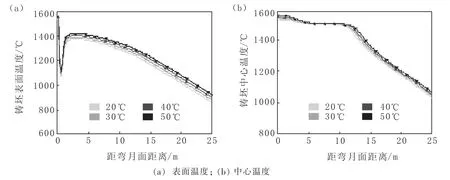
图6 不同过热度下铸坯表面温度和中心温度随距弯月面距离变化情况Fig.6 Changes of Surface Temperature and Center Temperature in Terms of Blank with Variable Distance of Meniscus under Different Degree of Superheat
2.3 二冷给水量对铸坯温度的影响
模拟二冷区给水量为最大给水量的40%、60%、80%和最大给水量,拉速为1.0 m/min,过热度为20℃,研究铸坯表面温度和中心温度变化规律,进而确定最佳给水量。不同二冷区给水量下凝固末端铸坯横截面温度场分布见图7所示。
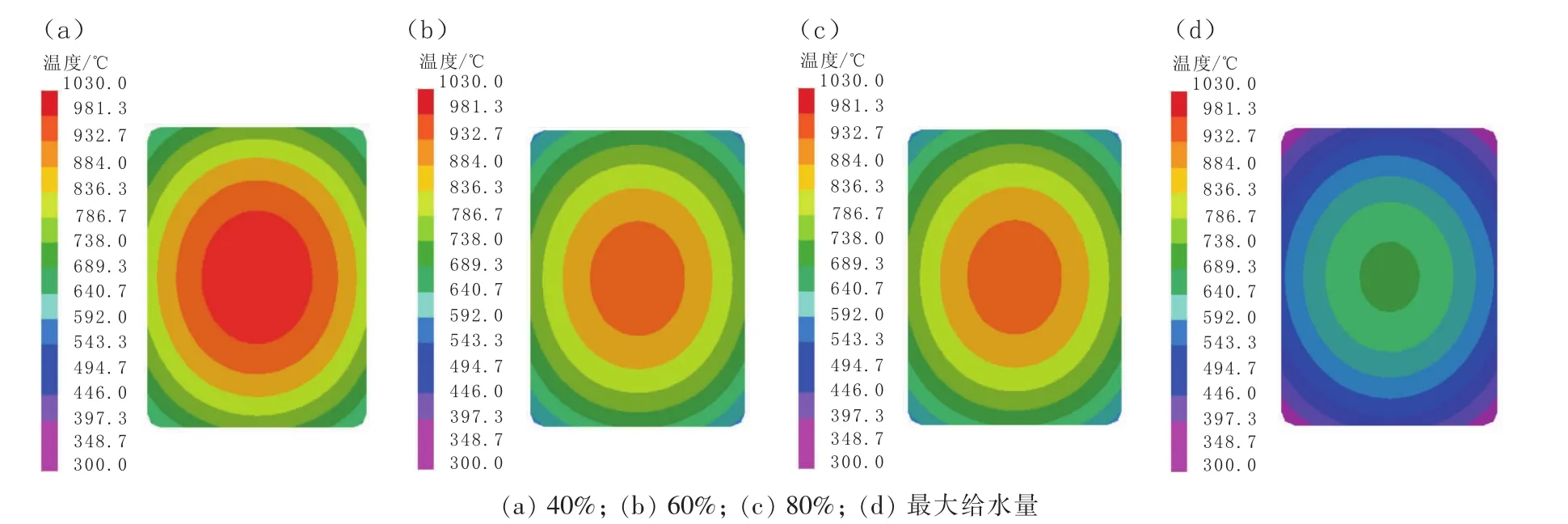
图7 不同二冷区给水量下凝固末端铸坯横截面温度场分布Fig.7 Temperature Field Distribution in Cross Section of Blank at Solidifying End-point under Different Water Supply Flow in Secondary Cooling Zone
从图7看出,随着二冷给水量不断增加,铸坯凝固末端中心温度呈下降趋势,二冷区给水量为最大给水量的40%、60%、80%及最大给水量时,凝固末端铸坯中心温度分别介于932.7~981.3℃、884.0~932.7℃、738.0~786.7℃及 689.3~738.0℃。 二冷区给水量每提高20%,凝固末端铸坯中心温度下降约50℃,可见二冷区冷却强度对铸坯温度变化影响较大,而中心温度越高,铸坯液芯越长,不利于钢水补缩。另外,二冷区给水量对铸坯表面温度和角部温度影响较大,二冷区给水量从40%增加到60%过程中,铸坯角部温度下降48℃;60%增加到80%和80%增加到最大给水量过程中,铸坯角部温度均下降146℃。
图8为不同二冷区给水量下铸坯表面温度和中心温度随距弯月面距离变化情况。
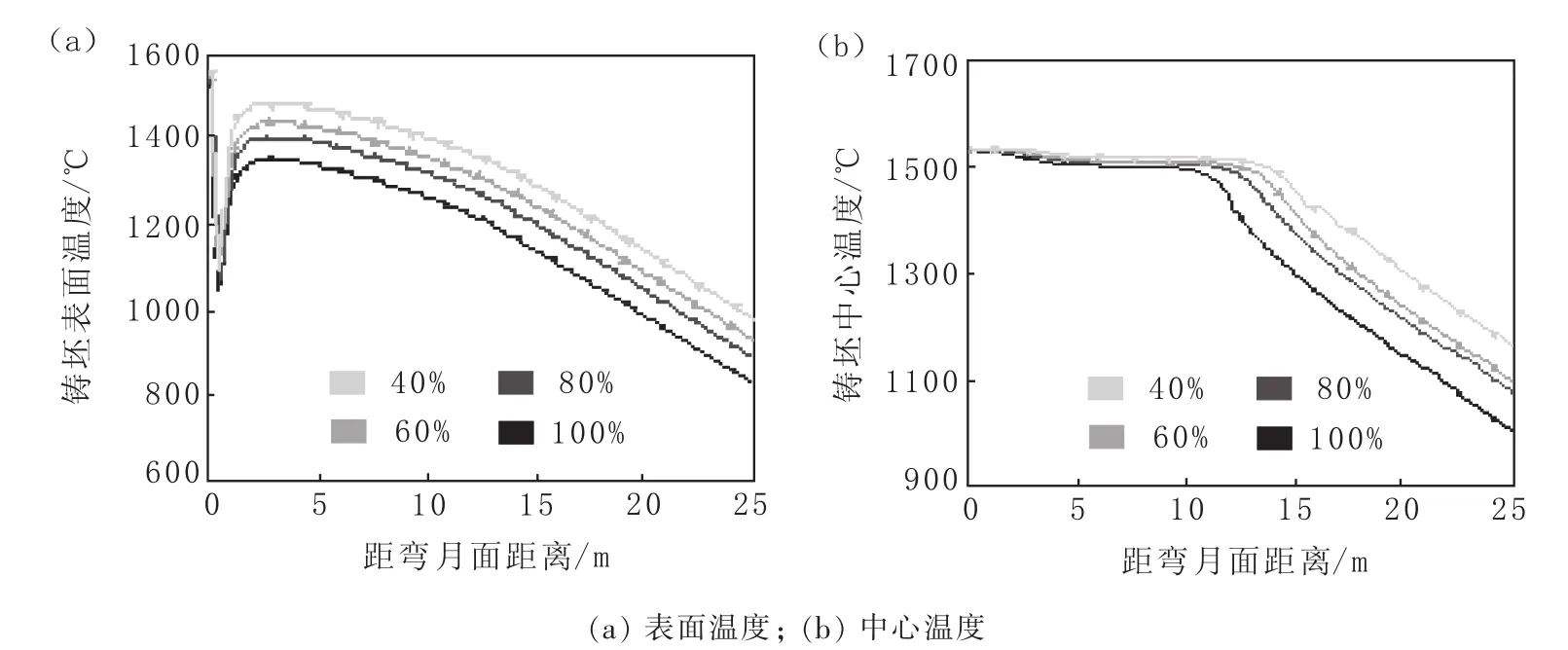
图8 不同二冷区给水量下铸坯表面温度和中心温度随距弯月面距离变化情况Fig.8 Changes of Surface Temperature and Center Temperature in Terms of Blank with Distance Changing from Meniscus under Different Water Supply Flow in Secondary Cooling Zone
从图8(a)可以看出,铸坯表面温度在出结晶器后都存在一个明显的回温趋势,这一趋势随着二冷区给水量的减少而增大。铸坯在出结晶器时表面温度降为1 050℃,当二冷区给水量为最大给水量时,铸坯表面最大回温温度为1 360℃,回温310℃;当二冷区给水量为80%、60%和40%时,铸坯表面最大回温温度分别为1 410、1 450、1 490℃,回温分别为370、410、450℃。 可见二冷区冷却强度对于铸坯表面温度影响较大,过大的回温现象会导致铸坯鼓肚以及在凝固前沿产生较大拉应力,这会促进疏松缩孔的生长。从图8(b)中可以看出,随着二冷区给水量的减少,铸坯中心温度下降临界点明显后移。当二冷区给水量分别为最大给水量、80%、60%、40%时,铸坯中心温度明显下降位置分别为距弯月面10.12、11.62、13.28、16.62 m处,铸坯中心温度下降临界点分别后移1.50、1.66、3.34 m。另外还可以看出,随着二冷区给水量的增大,凝固末端铸坯温度明显增大,40%的二冷区给水量比最大给水量的铸坯中心温度高160℃左右。而凝固末端铸坯的中心温度高,说明铸坯凝固时的液芯长度较长,不利于钢液补缩。
基于上述研究认为,凝固末端铸坯横截面中心温度高将导致液芯的长度增大,使补缩困难,从而产生缩孔,另外,铸坯表面温度的回升过于严重也将导致凝固前沿拉应力的产生进而产生内部裂纹。综合考虑,拉速为1.0 m/min,过热度为20℃,二冷区给水量为最大给水量时,对25MnSiV矩形连铸坯温度影响最小,有利于降低铸坯中心疏松缩孔比例。
3 结论
采用数值模拟的方法研究了拉速、过热度和二冷区给水量对25MnSiV矩形连铸坯表面温度和中心温度的影响,得出结论如下:
(1)拉速从1.0 m/min增大到1.6 m/min时,凝固末端铸坯横截面中心温度增加,而铸坯表面回温逐渐降低;过热度在20~50℃之间变化时,铸坯中心温度升高约60℃,而对铸坯表面温度影响不大;二冷给水量每提高20%,凝固末端铸坯中心温度下降约50℃,另外,铸坯表面回温随二冷区给水量增加而增加。
(2)拉速为1.0 m/min,过热度为20℃,二冷区给水量为最大给水量时,对25MnSiV矩形连铸坯的温度影响最小,有利于降低铸坯中心疏松缩孔比例。

