电网运行状态下的事故发生概率预测算法研究

喻寻，刘宁，严奉军，蒙雷，李义

(贵州电网有限责任公司毕节供电局， 贵州， 毕节 551700)

0 引言

在生活水平以及工业生产越来越离不开电力的现代社会中，电网早已经成为了国民经济发展的命脉，社会各阶层都对电网的性能提出了更高的要求。电网运行状态下如果发生事故，会直接导致整片区域的电力系统受到影响，进而造成巨大的经济损失，因此，保障电网的供电安全，避免大规模电网事故的发生成为了电力系统的主要任务。相关的研究人员为此设计了若干面对电网运行状态下事故发生概率预测的算法。

在现有事故发生概率预测方法研究中，有学者利用一个单调函数将所有数据特征权重串联起来，但是由于各类权重差异化较大，导致线性回归的预测模型所得到的结果数值准确性不高。有学者使用各项数据特征权重建立了多个数据树，并以此构建概率数据集，但是一旦权重发生变化，就会导致整个概率预测算法需要重新运算，不仅降低了预测效率，而且预测结果准确率无法得到保障。除此之外，还有学者利用回归分析的方式解释变量与概率之间的因果关系，一旦事件过于复杂就无法实现特征权重的量化分析[1-3]。文献[4]提出了一种基于溯因推理网络的电网故障预测方法，通过溯因推理网络对电网故障进行预测，将电网无故障运行时的数据与故障状态下运行时的数据进行对比，计算二者差值，实现故障预测。实验结果表明，该方法可以实现对故障的快速检测，但是存在检测结果准确性不高的问题。文献[5]提出一种基于历史故障信息的配电网设备故障概率建模方法，以实际历史故障记录信息为基础，分析设备故障机理。分析设备故障影响因素，分析各个故障因素之间的耦合关系，根据分析结果构建故障概率模型。实验结果表明，该方法同样存在预测结果误差较大的问题。

上述算法在高维数据融合后，在构建数据集的过程中都会出现较大的误差，导致电网事故发生概率预测算法精度较差。为解决以上问题，对数据特征提取以及融合的过程进行优化，并设计一种新的电网运行状态下的事故发生概率预测算法。该算法为了保证预测结果的准确性，在事故发生概率预测中充分考虑随机数的问题，避免模型产生过度拟合，从而实现提高预测结果准确性的目的。同时，在预测中通过放弃部分复杂数据的方式降低算法的复杂性，加快算法的响应速度，实现算法优化。

1 电网运行状态下事故发生概率预测算法设计

1.1 电网运行状态下计算数据融合特征权重

电网运行状态的数据中通常存在着较多无用以及冗余信息，因此想要得到能够代入的信息就需要对其进行筛选与提取。在表格处理工具中将原始数据按照一定的规则合并成一张大表，然后以一定的规则对数据进行过滤筛选。为了保证特征提取的准确性，所有数据必须完全从电网运行状态中复制下来，并经过噪音处理和异常值排查两个步骤。通常情况下，只有数值型的数据才可以作为能够直接进行特征提取的数据，因此需要对其中的一些文字型、符号型数据进行转换处理，然后将这些数据统一量化。量化时需要将这些数据的均值编码作为先验概率和后验概率的一个目标组合，将所有数据编制为一个训练集，并在其中使用以下计算公式计算先验概率。

(1)

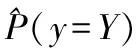
(2)

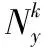
得到了先验概率和后验概率的计算方法后，就可以将这两项指标作为权重参数带入到训练集中。其后验概率越高，该概率的可信度就越高。权重参数可以通过式(3)计算：

(3)

式中，λ表示数据集的权重参数，n表示该特征值在数据训练中出现的次数，f表示该权重计算函数的参数，f越大，权重值随n变化的速度就越慢，e表示权重参数推导的量化差。如此就能够提取到电网运行状态下数据的融合特征，并计算其权重值。

根据上述分析可知，所提算法通过计算得到电网运行状态下数据融合特征的先验概率和后验概率，并将这两项指标作为权重参数带入到训练集中，得到数据融合特征的权重值。解决了传统方法由于不能准确计算各类差异化较大的事故权重数值，导致事故概率预测的精度较差的问题。

1.2 基于高维数据融合计算事故发生概率

通过上文中的先验概率、后验概率以及权重值的计算，能够得到从原因到结果的预测推理，此时应从近似推理的角度，通过一定的算法得到电网事故发生的概率，其计算的流程如图1所示。

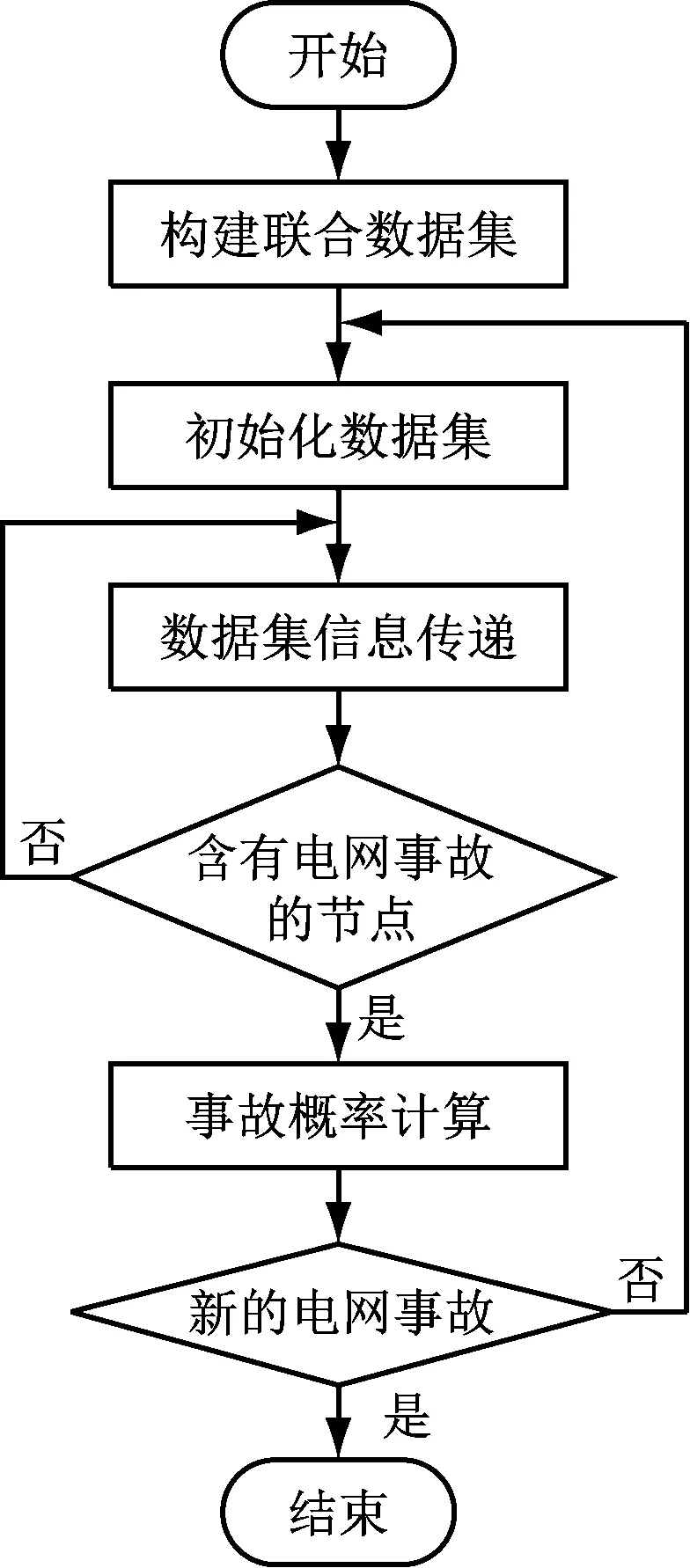
图1 概率计算流程图

如图1所示，概率计算过程中的首要步骤是进行数据集的初始化，即构建一个联合数据集，根据高维数据融合原理，设置CPT的分配参数，将G组织中的每一个团结点Xi作为一个覆盖家族的基团，然后将P(Xi|π(Xi))存储在团结点处，此时联合数据的观测值可以表示为xe:XE=xe。然后通过上文中的公式进行节点的数据传递与计算，每一个父节点都会与子节点两两相连，再经由子节点作为父节点向其他方向传递，从而形成一个树形的网络结构。信息传递主要可以分为两个主要阶段，分别是数据收集和数据分发阶段，通过选定一个包含父节点的团结点作为枢纽，从距离父节点最远处开始向父节点传递数据，直到将该条线路上的所有数据全部测定即可视为信息收集成功。而信息分发则正好相反，从父节点开始，向更远处传递数据，直至传递到最后一个子节点，如此将该数据集中的每一个节点遍历。在这个数据树中，由三角形的环是构成电网事故的节点，每一个节点包含四个或四个以上的子节点，通过以下公式可以使其三角化。

(4)

式中，P(Xf|XA)表示电网中事故概率的计算结果，Xf表示父节点，XA表示子节点，xa表示该子节点所在的节点数。每当有新的数据信息时，就需要重新初始化数据集，并再一次计算事故概率，直至所有数据计算完毕。

1.3 建立概率数据集的预测函数

根据上文中得到的概率数据，可以在设计电网事故发生概率预测算法的过程中首先构建一个基于概率数据集的训练样本X={(xa,ya)}，且a=1,2,3,…,n。上文中由树状节点预测集成函数相加所得的模型可以表示为

(5)

式中，M表示训练集数据树的分支数量，α表示最终预测值，fk(β)表示第k个分支样本的计算分值，且fk∈H，H表示一个由数据所组成的函数空间[6]。想要保证预测结果的准确性，就需要在该概率预测算法中考虑到随机数的问题，为了避免模型过度拟合，可以在数据中加入代数公式作为预测模型复杂度的控制公式：

(6)

式中，ϖ表示各概率数值的权重，λ、μ均为预测模型的参数，σ(fk)表示该数据集所得到的计算公式的复杂度，若σ(fk)>0.5，则可以放弃该部分数值，若σ(fk)<0.5，则可以将该数值作为预测算法的底层数据。通过放弃一部分复杂数据的方式降低算法的复杂性，加快算法的响应速度，对算法进行优化[7]。得到所有复杂度在0.5以下的所有数据以后，可以通过将目标函数展开为二阶泰勒公式的方式，移除常数项，并进一步提高实际预测值的精度。

(7)

式中，π(t)表示第t次迭代时的实际预测值,fi表示损失函数的一阶导数,gt表示预测算法中子节点的数目,yi表示预测遍历的次数,ti表示损失函数的二阶导数[8]。通过该公式，能够得到所有事故发生概率的预测集合，然后可以通过式(8)和式(9)选出各子空间中的最优函数值。

(8)

(9)

式中，ϖj表示第j个数据集的最优权重，Ο表示所有预测数据中的最优函数值，J表示衡量该算法精确度的函数，函数的数值越低，表示该算法预测的准确度越高[9]。如此就可以通过对观测数据预警的方式比较算法中各数据的准确度，最后选择一个数值最高的概率预测结果，作为最后的输出值，该输出值就是电网事故发生概率预测函数。

2 实验研究

2.1 实验数据准备

本文通过实验验证高维数据特征提取与融合的方法建立的概率预测算法，是否具备实效性和实时预测的准确性。在该实验中所使用的测试平台为一台具备Windows 10操作系统的计算机，其运行环境如表1所示。

表1 测试环境

将某电网系统一年内的电网运行数据作为原始资料，表2为具体的电网运行数据。

表2 电网运行数据

分别使用表格工具统计出详细的正负样本信息和特征分布结果，然后建立能够应用在函数模型中的数据集，对比基于单调函数的事故发生概率预测算法、基于数据特征权重的事故发生概率预测算法和基于回归分析的事故发生概率预测算法与所提算法的应用效果。

2.2 数据集性能测试

所提算法主要通过构建能够平衡各高维数据特征属性的数据集来对概率预测算法作出优化，因此可以通过对比数据集的方式判断不同算法的性能。为了保证实验结果的准确性，在数据集的构建中有两项必不可少的指标，分别是权重与编码，以下实验主要以这两项参数作为评价指标。权重衰减因数通常表示各项事件权重的影响参数，衰减因数越大，则该数据集的准确性越强。对编码因数的测试，则是因为通过数据子树节点可以将所有整条路径进行编码，进而实现对所有遍历路径的整理，因此编码因数越小，其所需要经历的概率数值就越小，计算结果越准确。在计算权重与编码因数时，将默认参数设置为0.063 3，得到的对比结果如表3和表4所示。

如表3所示，四种算法的权重衰减因数存在一定的差异，所提算法的权重衰减因数明显高于其他三种算法，其权重衰减因数最高值达到了0.87。表4中所提算法的编码因数均小于其他三种算法，其编码因数最低值仅为0.14。因此

表3 权重衰减因数对比

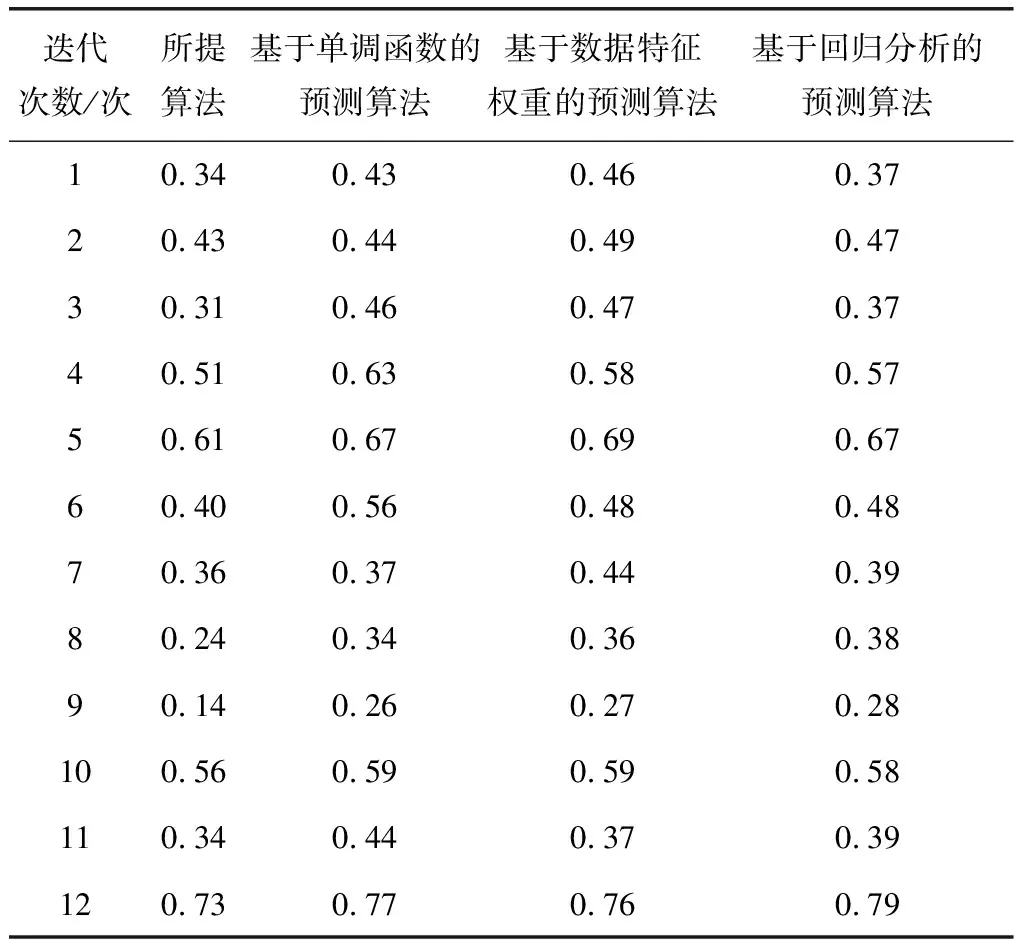
表4 编码因数对比

可以得知,所提算法建立的数据集准确度高于其他三种算法。

2.3 电网运行预测准确度测试

根据以上数据集，可以得到概率预测的函数模型，将该函数模型带入到原始数据中进行测试，通过前一刻的电网运行状态预测下一刻的电网事故发生概率。与当前的三种算法对比，以电网规模为横坐标，以预测的误差为纵坐标，得到如图2所示的实验图像。

如图2所示，曲线所代表的误差均在0以上，表示算法得到的概率预测数值均大于样本数据。而传统算法在概率预测中的误差大于所提算法，说明所提算法的预测精确度更高，误差最小。

图2 不同算法预测准确度对比

3 总结

上文基于电网运行状态下事故发生概率预测精度较低的问题构建了一个新的概率预测算法，并通过实验验证了该算法的准确性，相较于当前算法预测误差更小，能够为电网运维人员提供一定的支持。所提算法可以有效避免大规模电网事故的发生，对于电网供电安全保障领域具有一定的实际应用价值。