适用于低成本RFID系统的双向认证算法

卢爱芬

(广州科技职业技术大学，信息工程学院， 广东，广州 510550)

0 引言

射频识别系统一般包含电子标签、读写器、后台服务器三者。其中,电子标签因体积小、方便携带、易部署、成本不高、使用时间长等众多优势，使射频识别技术在很多领域中得到应用[1-3]。常见的电子标签一般有2种类型:一种是自身携带电源，可主动发起认证；另一种是自身并没有携带电源，无法主动发起认证，只能被动式响应读写器信息。现有的射频识别系统中，大多数用的电子标签还是属于无电源类型的[4-6]。

射频识别系统中经典的通信模型是读写器与后台服务器间有线链路实现交互，一般认为安全可靠；读写器与电子标签间采用无线链路，因无线链路自身具备的开放性，使得消息易被攻击者监听获取，存在安全隐患[7-8]。在早期的射频识别系统认证算法中，较多时候会采用经典的密码加密算法对所要发送信息进行加密，但现有的电子标签因低成本因素，使得电子标签计算能力受到严格限制，无法采用经典加密算法[9-10]。

文献[11]中采用简单的异或运算、与运算实现信息加密，但协议无法抵抗攻击者发起的物理攻击，攻击者物理攻击成功后，可对标签发起假冒攻击。文献[12]中采用物理不可克隆函数对信息加密，算法虽具备一定安全性，但因读写器端未存放前后轮会话共享密钥，使得协议无法抗去同步化攻击。文献[13]中采用经典的HASH函数实现信息加密，文献[14]中算法对文献[13]中算法进行了详细安全性分析，指出文献[13]中算法无法提供会话实体间双向认证缺陷，同时算法还无法抗攻击者发起的假冒攻击安全缺陷。

针对现有大多数双向认证算法或存在安全隐患或存在计算量大无法适用低成本RFID系统等不足，文中在结合众多协议基础之上，设计一个采用变形反比例函数实现加密的双向认证算法。

1 双向认证算法

本小节首先介绍算法中涉及的符号含义，然后给出文中算法加密用的变形反比例函数具体定义，最后给出算法。

1.1 算法符号含义

R表示读写器；

T表示电子标签；

ID_L表示电子标签标识符左边一半；

ID_R表示电子标签标识符右边一半；

ID表示电子标签标识符；

K表示电子标签与读写器间共享秘密值；

Knew表示电子标签与读写器间当前共享秘密值；

Kold表示电子标签与读写器间上轮共享秘密值；

Gf(x,y)表示变形反比例函数；

a表示电子标签产生的随机数；

b表示读写器产生的随机数；

&表示按位与运算；

⊕表示按位异或运算。

1.2 变形反比例函数

变形反比例函数按照如下方式定义：约定x、y都是长度为L位的二进制串；hm(x)、hm(y)分别表示二进制串x、y的汉明重量值；变形反比例函数一般形式如y=m/x+n。当hm(x)>hm(y)时，取hm(y)的值作为上述一般形式中m的值，取hm(x)的值作为上述一般形式中n的值，同时对参数y进行反比例函数加密计算。当hm(x)≤hm(y)时，取hm(y)的值作为上述一般形式中n的值，取hm(x)的值作为上述一般形式中m的值，同时对参数x进行反比例函数加密计算。为便于文中有关变形反比例函数描述，文中统一用符号Gf(x,y)表示。

即如下：

(1)

1.3 算法步骤描述

与文献[15]一样，做出如下约定：读写器与数据库间采用有线方式交互消息，安全可靠，故将二者看成一个整体。文中算法在认证之前有一个初始化过程，初始化过程完成，R端储存信息有ID_L、ID_R、K，T端储存信息有ID_L、ID_R、K。具体流程如图1所示。

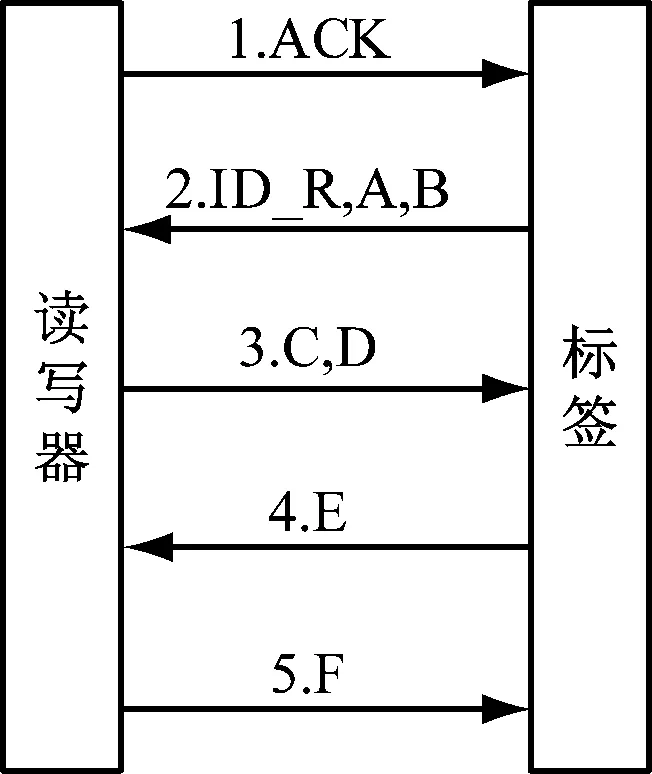
图1 双向认证算法

结合图1可将文中基于变形反比例函数的双向认证算法具体步骤描述如下。

步骤1 R向T发送ACK认证请求命令，开始认证过程。

步骤2 T产生随机数a，计算得到消息A=a⊕ID_L、消息B=Gf(a,ID_L)，并将ID_R、A、B发送给R。

步骤3 R将依据收到的ID_R在数据库中查找是否存在该数据。未找到，则算法停止。找到，R可将与ID_R相关联的信息全部取出来。先对A进行变形A⊕ID_L可得到随机数a′，然后计算得到B′=Gf(a′,ID_L)，接着对比B′与B的关系。

B与B′不等，算法终止;如果相等，说明T通过R的验证。R开始产生一个随机数b，计算得到消息C=a⊕b、消息D=Gf(a,b)，并将C、D发送给T。

步骤4 T将对C进行变形处理C⊕a可得到随机数b′，计算得到D′=Gf(a,b′)，然后对比D′与D的值。

D与D′不等，算法终止;如果相等，说明T对R的验证完成。T计算得到消息E=Gf(a⊕D,b)，并将E发送给R。

步骤5 R计算得到E′，对比E′与E的大小关系。

E与E′不等，算法终止;如果相等，说明R完成对T的验证。R计算得到消息F=Gf(a&b,K)，开始更新信息，信息更新完成后，将F发送给R。

当*=old时，Knew=Gf(a,b⊕Kold)。

当*=new时，Kold=Knew、Knew=Gf(a,b⊕Knew)。

步骤6 T收到信息后，T计算得到F′，并比较F′与收到F的大小。

F与F′不等，算法终止。如果相等，表明R通过T的验证。T开始更新信息K=Gf(a,b⊕K)。T信息更新完成后，则双向认证完成。

2 算法安全性分析

双向认证。通信实体间能够对彼此的真伪进行验证是算法最基本的安全需求。文中算法R与T间的双向认证都分2次进行，在步骤3中,R通过A、B完成第一次对T的认证；在步骤5中,R再次通过E完成第二次对T的认证。在步骤4中,T则是通过C、D第一次完成对R的认证;在步骤6中,T将再次通过F完成第二次对R的认证。基于上述，文中算法可以实现通信实体间的双向认证。

假冒攻击。当攻击者假冒成R时，攻击者可以接收到合法T发送来的消息ID_R、A、B，但因攻击者不知晓ID_L值，攻击者无法从消息A、B中破解出有用的隐私信息，使得攻击者计算的消息C、D值并不是正确的值；当T收到攻击者发送来的C、D消息时，T只需要进行简单的计算，即可识别出消息来源是攻击者伪造的。当攻击者假冒成T时，攻击者会随机选择数据进行消息A、B的计算；当R收到攻击者发送来的消息时，R对A、B进行简单验证，即可辨别出消息发送方是攻击者伪造。基于上述，算法可以抵抗假冒攻击。

重放攻击。攻击者窃听当前会话过程，可以获取当前会话过程中所有消息，在下一轮会话过程中重放当前窃听所得消息，以企图通过某会话实体验证，从而达到破解隐私信息目的。文中算法采用信息加密过程中混入随机数方法来解决攻击者发起的重放攻击，当攻击者重放上轮消息时，本轮消息加密过程中用到的随机数已发生变更，使得攻击者重放的消息无法通过验证。鉴于随机数由随机数发生器随机产生，具有无法预测性，因此攻击者无法预测下轮会话用到的随机数。基于上述，文中算法可抵抗重放攻击。

追踪攻击。文中算法所有消息都是加密之后在发送，攻击者获取的消息都是密文，无法直接破解出有用信息。信息加密通过混入随机数方式，使得前后两轮会话同一个会话实体计算所得消息值也是不同的，这样攻击者就无法从获取的消息中分析出电子标签的位置，无法实施追踪攻击。基于上述，文中算法可抵抗追踪攻击。

异步攻击。文中算法在R一端存放有当前会话、上轮会话过程中R与T间的共享秘密值，以此来抵抗异步攻击。具体在算法步骤5中，R会先用Knew来发起对T的验证，验证通过，可直接进行后续操作；若验证失败，则R会再次用Kold来发起对T的验证。当且仅当，前后两次对T的验证都失败，算法才会终止。基于上述，文中算法可抵抗异步攻击。

后向安全。攻击者想要从获取的当前会话消息中分析部分隐私信息，然后用此信息再来逆推出上轮会话中部分隐私信息，该种攻击方式称为后向安全攻击。文中协议在信息加密时候引入随机数，使得前后消息值不同；加之随机数具有随机性、前后无关联性、互异性等特征，使得攻击者无法从当前获取消息逆推出上轮消息加密用到隐私信息。基于上述，文中算法具备后向安全性。

将本文算法与其他算法之间进行安全性对比分析结果如表1所示。在表1中，√表示能够抵抗该种类型攻击，×表示无法抵抗该种类型攻击。

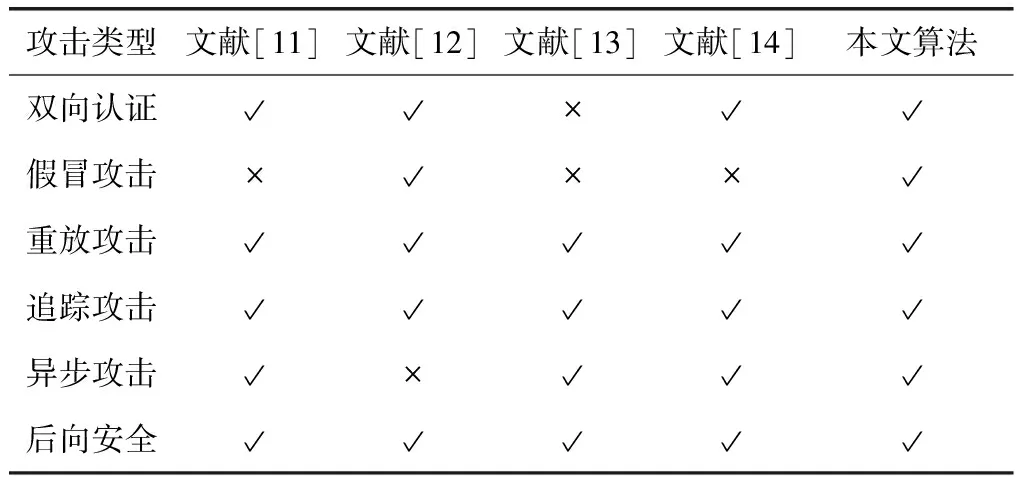
表1 不同算法间安全性对比

3 算法性能分析

本文选择电子标签作为性能分析对象，选择电子标签为对象的因素有：电子标签满足低成本要求，使得电子标签计算能力及存储空间严重受到制约。从电子标签一端的计算量及存储量角度出发，将本文算法与其他算法进行性能比较，分析结果如表2所示。

对表2中出现的符号所表示的含义解释如下：AND符号表示按位与运算、OXR符号表示按位异或运算、PUF符号表示物理不可克隆函数、HASH符号表示哈希函数、Gf符号表示变形反比例函数、L符号表示会话消息长度。

在上述不同的运算算法中，不同的算法自身具备的计算量大小不同，其中AND、XOR、Gf三种运算都是基于按位运算实现，因此三者都属于超轻量级的运算；而PUF、HASH两种运算则是属于轻量级的运算。基于上述，本文算法与文献[11]中算法在电子标签一端的计算量应是大致相当；本文算法在电子标签一端的计算量要优于文献[12-14]中电子标签一端的计算量。

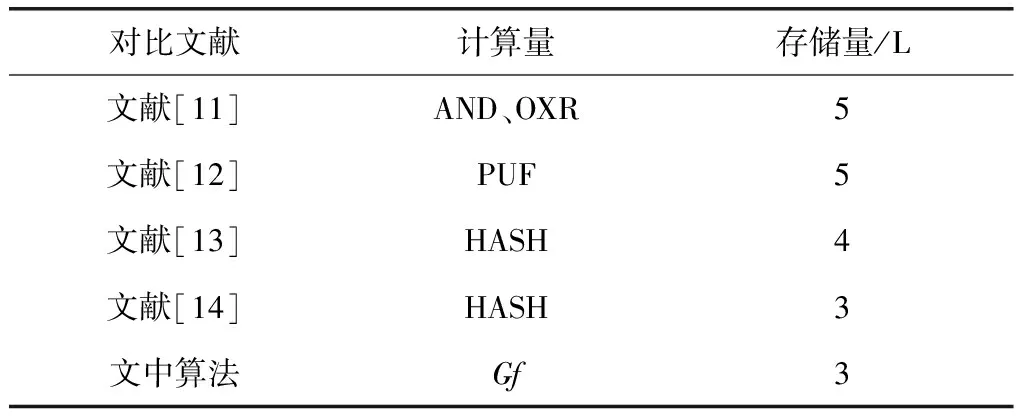
表2 不同算法间性能对比

从电子标签一端的存储量角度分析，本文算法电子标签一端需要存放的信息有：ID、K、a，因此存储量大小为3L。与其他算法相比较，要少于其他算法电子标签一端存储开销。

综合表2中计算量、存储量角度分析，文中算法虽与文献[11]中电子标签一端计算量相当，但存储量角度有减少，且文中算法可以弥补文献[11]中算法存在的安全不足；文中算法计算量要少于文献[12-14]中电子标签计算量，具备推广优势，同时文中算法可以弥补上述文献中算法存在的安全漏洞。

4 总结

本文给出一个基于变形反比例函数实现的双向认证算法。算法采用变形反比例函数实现对信息加密，根据变形反比例函数定义可得，算法计算量能够达到超轻量级别；同时变形反比例函数充分利用加密参数自身汉明重量参数，能够减少参量的引入，从而可降低存储量。文中最后从多个角度对文中算法进行了详细的安全分析，表明文中算法可抵抗重放攻击、异步攻击、假冒攻击等常见类型的攻击，具备较高的安全性能；性能对比角度，表明文中算法具备低计算量特征，能够在现有低成本RFID系统中推广使用。