基于灰色关联法与FAHP的磨煤机能耗分析

刘文静,靳 岚,张金刚,乔 治

(1.兰州信息科技学院,甘肃 兰州 730300; 2.兰州理工大学机电工程学院,甘肃 兰州 730050;3.天津国投新能源有限公司,天津 300100; 4.冠一科仪集团有限公司,广东 广州 510630)

磨煤机工作效率高、出力大、解耦性强,是燃煤火力发电机组制粉系统的重要设备[1]。双进双出钢球磨煤机属于低速磨煤机,具有生产效率高、无故障运行时间长、性能稳定、适应性范围广等优点,被广泛应用于不同行业[2-3]。建立煤粉粒度与制备过程能源消耗的平衡关系,可以在确保煤粉粒度的同时,使生产能耗达到最优[4-6]。

谷俊杰等[7]考虑质量与能量平衡,建立了双进双出磨煤机制粉系统模型,提高了系统运行的安全性与经济性。曹丽华等[8]运用灰色关联度方法对五家电厂节能减排指标进行了分析,得出准确评价指标,经验证与实际情况一致,该综合评价方法有较强的可操作性。王群等[9]计算出电力系统通信预案的可靠程度量值,是运用模糊层次分析法定性定量分析的结果,在量化分析过程中对应急预案的薄弱环节查缺补漏,提高和优化了安全体系。

运用灰色关联法建立复杂生产系统多目标的影响因素模型,定量分析各因素的关联程度。模糊层次分析法(FAHP,fuzzy analysis hierarchical process)对目标函数评估时的不确定性进行量化,便于分析多目标多因素的权重及影响程度,大量有益的研究也充分证明模糊层次分析法的有效性。通过此方法可观察系统因素与主体要素之间变化趋势的关联性[10-11]。

1 灰色关联度分析

运用灰色关联度理论,建立采集数据动态GM数学模型,结合灰色关联度分析理论,确定各因素的影响程度及预测模型[12]。

1.1 建立数据库

评价指标体系对模型的影响至关重要,根据评价目的确定评价指标体系。原始序列为

(1)

其中:m为指标的个数;n为采集样本数。影响因素数列构成参考数据X′i，即

X′i=(x′i(1),x′i(2),…,x′i(m))T,i=1,2,…,n

(2)

评价目的选择主体要素X′0,即

X′0=(x′0(1),x′0(2),…,x′0(m))。

1.2 数据无量纲处理

为了消除数据之间不同数量级的影响,将不同单位的数值进行标准化处理,无量纲化后的数据序列矩阵如下:

1.3 关联系数

关联系数ξi表示为

(3)

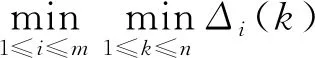
文献[13]中采用数学推倒的方法对分辨系数做了定量分析,可以有效提高各因素之间关联度的判别能力。所有差值绝对值的均值Δv表示为

且Δi(k)=|x0(k)-xi(k)|,故上式可表示为

(4)

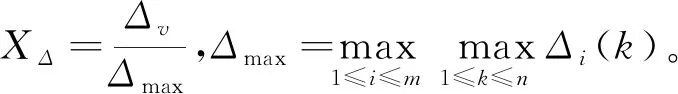
要求ρ的取值范围为ρ∈[XΔ,2XΔ];若Δmax>3Δv时,XΔ≤ρ≤1.5XΔ;若Δmax≤3Δv时,1.5XΔ≤ρ≤2XΔ。

1.4 关联度

关联度大小可以表征各因素的影响程度,即各影响因素与参考序列对应元素的关联系数的均值，关联度记为γi，表示为

(5)

其中：k=1,2,…,n;i=0,1,2,…,m。

2 模糊层次分析法(FAHP)理论

为了验证关键影响因素,采用模糊综合评判方法分析影响能耗的重要因素。模糊综合评判方法[15]可以定性评估各因素的影响层次,运用专家估计法两两对比进行量化分析,确定各因素的重要性。

层次分析法(AHP,analysis hierarchical proces)可以对影响因素进行两两对比,用量化指标表示对比结果,定性定量处理影响主体目标的各个因素的重要性,具有全面、便捷的优点[16]。模糊层次分析法(FAHP)分析多因素对主体目标的影响程度时,在数据样本量受限制的情况下,可对不同维度的指标定量化分析,增强模型的辨识能力,解决各因素之间的相似性或模糊性。

2.1 建立分析要素

建立因素集,即影响主体目标的各因素集合，记为C,C={c1,c2,…,ci}。建立评判集,即被评判因素的评价集合，记为V,V={V1,V2,…,Vi},Vi代表第i个因素的评价指标。

2.2 构造模糊判断矩阵

FAHP引入了模糊综合评价法来改进AHP,任意一个模糊集都对应一个隶属函数,选用不同的隶属函数可以提高模型评价效果[17]。FAHP常用隶属函数中的三角模糊数是特殊的梯形分布函数,可以很好地表达某一因素的影响程度。

构造正互反模糊判断矩阵,记为M：

(6)

2.3 计算初始权重

初始权重表示为

(7)

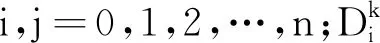
2.4 去模糊化,计算最终权重

初始权重去模糊化,得到各因素的最终权重。若D(ci)=(li,mi,ui)为影响因素ci的初始权重,D(cj)=(lj,mj,uj)为影响因素cj的初始权重,则D(ci)≥D(cj)的可能度为K,用三角模糊函数定义为

K(D(ci)≥D(cj))=

(8)

d(ci)=∧(K(Di>D1),…,K(Di>Dn)),

(9)

其中：d(ci)为影响因素ci的最终权重。

以此类推,得出所有影响因素的最终权重集,设为W:

W=(d(c1),d(c2)，…，d(cn))。

(10)

2.5 权重值标准化

将ci的最终权值进行权重标准化,即归一化处理:

(11)

以此类推,得到c1,c2,…,ci归一化权重集为

ω′ci=(ωc1,ωc2,…,ωci)。

(12)

3 实例分析

3.1 建立模型

针对兰州某火电厂300 MW燃煤机组,制粉系统选用双进双出BBD3854磨煤机进行建模,电动机型号为YTM560-6,1 120 kW,6 kV,985 r/min。

3.2 模型量纲化

运用Matlab建立灰色理论分析模型,根据评估目标设定耗电量为主体参数,记作

X′0=[84 85 84 83 81 81 78 81 78]。

影响电能消耗的各因素分别为:二次风压x1,磨煤机入口热风开门度x2,磨煤机入口压力x3,磨煤机进、出口压差x4,钢球装载量x5,即

运用Matlab建立分析预测模型,采用初值化变换法进行数据处理:

3.3 计算关联度

计算磨煤机能耗评价对象指标与其他参考序列对应项的绝对差值Δi(k),代入式(3)中计算关联系数,确定各因素与能耗的关联度。

依此方法选择不同的分辨度系数,运用Matlab软件进行对比分析,以期达到准确的重要度排序。选择多个分辨度系数作对比分析,可以提高分析的准确性,确定模型分析能力。分辨系数及关联度排序如表2所列。

表2 关联度排序

分辨度系数不同时会引起各因素关联度的排序变化。表2数据排列顺序中都可确定x1、x4、x3的影响程度均小于x2及x5,当ρ取值0.23、0.3、0.35、0.5、0.8时x1、x4、x3的排列顺序一致,仅当ρ取值在计算区域之外为0.1时,影响各因素的重要度x1、x4、x3排序发生变化,虽然整体比较相近,但是影响较小的因素序列改变。对比生产实际情况,关联度序列对分辨系数依赖性较大,依据文献[13]中计算的分辨系数取值范围与通常取值0.5得出结论一致,即x5>x2>x4>x3>x1,即钢球装载量>磨煤机入口热风开门度>磨煤机进、出口压差>磨煤机入口压力>二次风压。

分辨系数取值大小会对关联度分布区间产生影响,如图1所示。ρ取值大小影响各因素的关联度序列,但是辨识度系数大小仍体现了系统的整体性,主要影响因素序列平稳,仅在小范围局部发生波动。通常ρ取值0.5可以减少运算时间,提高分析效率,有效得出关键影响因素,具有客观依据和更好的适应性。

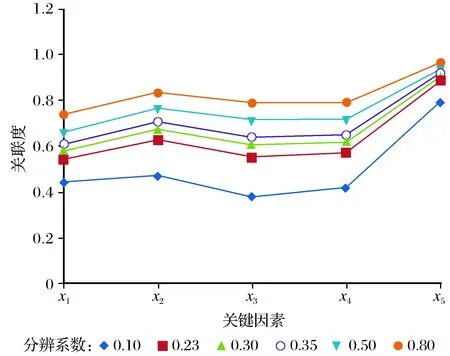
图1 关联度分布

分辨系数从0.1到0.8时关联度发生变化,分辨系数取值增大时重要度区间减小,影响程度相近的因素辨识度下降,需要提高计算精度,增加运算时间,降低了分析效率;分辨系数取值减小时重要度区间增大,各因素之间的分辨能力增加,特征明显,但是取值过小会影响关联度序列,增大误差。

3.4 FAHP分析重要度

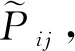
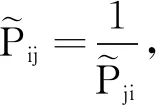
将模糊判断矩阵M代入式(7)计算得

Dc1=(0.155 63,0.256 17,0.379 60),Dc2=(0.119 95,0.153 40,0.191 99),

Dc3=(0.163 82,0.206 59,0.287 46),Dc4=(0.170 50,0.222 76,0.286 70),Dc5=(0.121 73,0.161 08,0.211 07)。

将上述各因素影响权重去模糊化处理,计算可能度:

∵K(D(c1)≥D(c2))=1，K(D(c1)≥D(c3))=1，

K(D(c1)≥D(c4))=1，K(D(c1)≥D(c5))=1。

根据三角模糊函数计算式(8)和式(9),可以得出初始权重d(ci)为

∴d(c1)=∧(K(D1>D2),…，K(D1>D5))=

∧(1,1,1)=1。

同理计算d(c2):

∴d(c2)=∧(K(D2>D1),…，K(D2>D5))=∧(0.261 3,0.346 3,0.236 5,0.901 4)=0.236 55。

同理可得

d(c3)=0.726 99，d(c4)=0.796 87，

d(c5)=0.368 28。

所有影响因素的最终权重集W为

W=(1,0.236 55,0.726 69,0.796 87,0.368 28)。

将上述最终权重集数据归一化处理,进行重要因素排序,权重集为

ω′ci=(0.319 65,0.075 61,0.232 29,0.254 72,0.117 72)。

根据以上分析因素进行排序,为c1>c4>c3>c5>c2,即影响因素从大到小的顺序依次为钢球装载量>磨煤机入口热风开门度>磨煤机进、出口压差>磨煤机入口压力>二次风压。

运用FAHP分析得出的重要度排序与灰度理论分析的关联度结论一致,对比建立的理论模型与专家评估结果一致,有效验证了各因素的重要程度,结论为优化生产指标提供了参考依据。

4 结论

应用灰色理论对磨煤机的运行参数进行分析,建立各因素对能耗指标关联度的预测模型。关联度大小表征了对能耗指标的影响程度,并且当分辨系数取值较小时分布区间增大,增强了分辨效果;当分辨系数取值较大时,分布区间缩小,可辨效果下降,因此分辨系数取值对各因素的分布区间及辨别效果影响较显著。但分辨系数取值不同时,得出的结论总体趋势相似，局部特征有差异,为今后相关理论分析提供了参考。

通过灰色关联度计算结果可以直观看出主体因素与各相关影响因素的关联度程度,其中钢球装载量对主体因素影响明显,其他因素对电能消耗影响程度不同,该结论与FAHP分析各因素最终权重相一致,与生产实际相符。经过验证研究所运用的方法对电能消耗的控制可行并且有效,该预测模型预测较准确,符合实际作业状况。依据输入参数影响程度调整磨煤机运行参数,用此模型优化系统指标,可以在生产运行中确保磨煤效率和出力的基础上,控制能源消耗,降低生产成本,减少能耗,从而逐步实现绿色生产。