uBlock类结构最优向量置换的高效搜索

李晓丹 吴文玲 张 丽

1(中国科学院软件研究所可信计算与信息保障实验室 北京 100190) 2(中国科学院大学 北京 100049) 3(中国星网网络系统研究院有限公司 北京 100083)

在分组密码的设计和分析中，整体结构是首要的研究对象.作为分组密码的重要特征，整体结构对于分组密码的轮数选取、软硬件实现性能都有非常大的影响.常用的分组密码整体结构有：Feistel结构、SP结构、广义Feistel结构、MISTY结构、Lai-Massey结构以及由上述结构彼此嵌套形成的细化整体结构.其中，SP结构非常清晰，是直接基于香农的“混淆”和“扩散”原则实现的整体结构，通常包含一个可逆的非线性函数S和一个可逆线性变换P，其中S层起混淆作用，线性层P起扩散作用.当给定S层和P层的某些密码指标，设计者可给出SP密码抵抗差分分析和线性分析的可证明安全.相较于Feistel结构，SP结构扩散速度更快，但是为达到加密和解密的相似性需要合理设计密码部件.SP结构的分组密码算法有：AES[1],ARIA[2]和Serpent等.其中AES无疑是目前最重要的分组密码，它的扩散层由2部分组成，也被称为两级扩散层，一部分是选取分支数最大的MDS矩阵作为列混淆，另一部分是行移位操作.特别地，许多分组密码和杂凑函数的设计都是从AES的初始设计结构开始，对一个或多个部件进行调整以满足其设计要求，如Anubis[3]，LED[4]，Midori[5]，PHOTON[6]，QARMA[7]，SKINNY[8]和Whirlpool[9].此类算法的线性层本身由2部分组成:一部分类似于AES的列混合操作，另一部分类似于AES行移位操作，我们称这类密码算法为类AES密码算法.列混合操作是对状态列的矩阵乘法，行移位操作是对状态字的置换.对于前者，研究结果较多，只需要保证其具有高的分支数，分支数越高，对应的活跃S盒数越多，则抵抗差分分析和线性分析的能力越强.AES选取的列混合操作为分支数最大的MDS矩阵，而出于轻量化考虑的一些算法，如Midori，SKINNY等，则采用非最优分支数的二元矩阵.而对于字换位操作，当仅考虑超过2轮的情形时，字换位的选取极大影响活跃S盒的数量，因此，对于好的设计来说，精心选择字换位操作至关重要.对于AES，得益于宽轨迹设计策略[10]，可以获得数学上可证明的最小活跃S盒数的界限，保证4轮后至少有25个活跃S盒.Midori算法设计的初衷是减少硬件资源损耗，它采用类似于AES算法的结构，与SKINNY算法类似，它们都属于类AES算法，但是在列混淆部分选用非最优分支数的矩阵.Midori设计者发现使用分支数为4的二元矩阵时，4轮后活跃S盒数下降到16个，但改变字换位操作可显著提高活跃S盒数.2015年，文献[11]证明了对于选用最优分支数的列混合操作的算法，用任意置换替换字换位操作不能增加活跃S盒的数量.2016年，文献[12]给出，用B表示矩阵的分支数，对于经典字换位操作，则对于列混合为MDS矩阵的，4轮后至少有B2个活跃S盒；对于列混合为二元矩阵的，4轮后活跃S盒的下界可能大于B2，且对于某些二元矩阵，下界可达到B(B+2).2018年，文献[13]提出一种加速搜索字换位操作的技术，并应用于Midori和SKINNY算法，寻找使得整体扩散性更好的字换位操作.这也是现在轻量级分组密码的一个设计趋势，扩散层选择非MDS矩阵，虽然扩散效果没有MDS矩阵好，但是实现效率会有很大提高,这在资源受限的环境下有很大优势，而且在结合合适的向量置换操作后，整体算法也可以达到较好的扩散性和安全性.因此，使用类AES结构来设计轻量级分组密码是一个不错的选择，特别是列混合操作选用最优二元扩散层,并结合恰当的向量置换，可以很好地平衡安全性和实现代价，然而在选定列混合操作后，搜索合适的向量置换并不容易，这也是这类算法在设计时需要花费大量精力的部分.

uBlock算法[14]是全国密码算法设计竞赛中的获胜算法.该算法是经典的SP结构，是一种典型的类AES算法，线性层选用的是16维的最优二元扩散层与向量置换的组合，扩散速度快且可以在各种软硬件平台上高速实现.受文献[13]的启发，本文研究了uBlock类结构的扩散性，并给出了寻找最优置换的搜索策略.通过对uBlock类结构中二元扩散层性质的研究，我们给出uBlock类结构全扩散轮数的下界.根据结构特点，我们揭示了uBlock类结构等价类的划分准则，并基于此给出了uBlock类结构最优向量置换的搜索策略.最后根据128 b和256 b分组的uBlock类结构的特点，进一步优化了搜索策略，并依据全扩散轮数、性能和超级扩散层的分支数3个指标，给出了128 b和256 b分组的uBlock类结构的一系列最优向量置换.我们的方法可以大幅度降低需要测试的置换对，为后续uBlock类算法的设计提供技术支持.

1 基础知识

本节介绍相关的基础概念和定义.

1.1 符号表示

表1给出了本文中使用的符号:

Table 1 Symbols

1.2 分支数

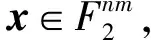
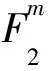
M的线性分支数定义为

分支数反映了密码方案的扩散性，此外也与差分分析和线性分析相关.分支数达到最大的矩阵称为MDS矩阵，分支数达到次优的矩阵称为Near-MDS矩阵.基于分支数，密码方案的设计者和分析者可以估计活跃S盒的下界，从而评估算法抵抗差分分析和线性分析的能力.

1.3 uBlock算法描述

uBlock算法的整体结构采用PX(Pshufb-Xor)结构(SP结构的一种细化结构)，Pshufb和Xor分别是向量置换和异或运算指令.算法设计采用S盒和分支数的理念，对差分分析和线性分析具有可证明的安全性，同时对于不可能差分分析、积分分析、中间相遇攻击等分析方法具有相对成熟的分析评估理论支持.此外，uBlock算法适应各种软硬件平台，充分考虑了微处理器的计算资源,可以利用SSE,AVX2和NEON等指令集高效实现；硬件实现简单而有效,既可以高速实现，满足高性能环境的应用需求,也可以轻量化实现,满足资源受限环境的安全需求.

uBlock是一族分组密码算法，分组长度和密钥长度支持128 b和256 b，分别记为uBlock128/128,uBlock128/256和uBlock256/256，迭代轮数分别为16,24和24.加密算法由轮迭代变换组成，轮变换如图1所示:

图1中，基本模块为：

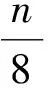
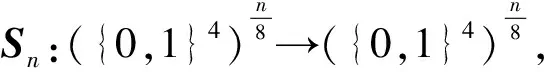
4 b的S盒如表2所示：

Table 2 The 4 bit S Box of uBlock Algorithm

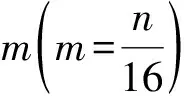
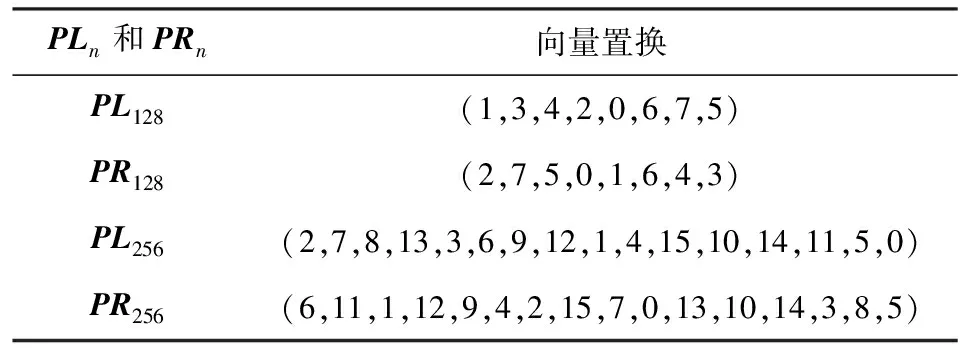
Table 3 PLn and PRn

比如PL128表示为

PL128:({0,1}8)8→({0,1}8)8

(y0,y1,…,y7)→(z0,z1,…,z7)

z0=y1,z1=y3,z2=y4,z3=y6,

z4=y0,z5=y2,z6=y7,z7=y5.

2 uBlock类结构

uBlock算法采用的整体结构是PX结构，其扩散层由2部分组成：一部分是线性变换，即由Feistel结构构造的二元最优扩散层；另一部分是向量置换.在本节中，我们探索一类PX结构的扩散特性，即线性变换部分选取与uBlock算法相同的二元扩散层，向量置换部分与uBlock算法不同的结构，称之为uBlock类结构，形式如图2所示：

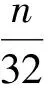
此外，我们观察到M16用矩阵形式表示出来，恰好为如下形式的分块矩阵：

其中,

A=Circ(0,0,1,1,1,0,1,1),

B=Circ(1,1,0,1,0,1,1,1),

C=Circ(1,0,1,1,0,0,1,1).

由于

因此

其中Am,Bm,Cm指对角线元素分别为A,B,C，而其余元素为零矩阵的m×m分块矩阵，即有

我们的目标是探索uBlock类结构的扩散性，并寻找最优的向量置换使得整体结构的扩散性和安全性达到最优，即我们需要考虑的指标有3个：

1)全扩散轮数.全扩散轮数越小，算法的扩散性越强，且可以根据全扩散轮数大致估计算法抵抗不可能差分、积分分析等结构性分析方法的能力.因此，我们旨在寻找可以达到最小全扩散轮数的置换.

2)实现性能.尽可能减少软件实现中的指令数.

3)4轮超级S盒下的分支数.我们可以根据分支数的概念给出算法活跃S盒的下界，并基于此估计其抵抗差分和线性分析的能力.因此，我们希望分支数越大越好.

2.1 全扩散轮数

扩散最初是由香农在文献[15]中定义的，意思是一个子块的输入影响全部子块的输出.文献[16]证明了抵抗饱和攻击和不可能差分攻击的轮数与称之为全扩散轮数的概念相关,用DR表示全扩散轮数.同时，证明了给定的结构需要至少2DR+1轮来抵抗上述攻击.因此，在设计分组密码时,全扩散轮数是一个重要的参考指标.接下来,我们研究uBlock类结构全扩散轮数的下界,首先给出M16的扩散性质：

性质1.输入向量的汉明重量为1时,经过M16均可扩散到11个位置.

性质2.输入向量的汉明重量为2时，有如下8种情形在经过M16后可全扩散：

(1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0),

(0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1),

(0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0),

(0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0),

(0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0),

(0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0),

(0,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0),

(0,0,0,0,0,0,0,1,0,0,0,0,0,1,0,0).

性质3.输入向量的汉明重量为3时,有400种输入在经过M16后可全扩散,剩余160种输入均可扩散到15个位置.

性质4.输入向量的汉明重量为4时,有1 740种输入在经过M16后可全扩散,剩余80种输入均可扩散到15个位置.

性质5.输入向量的汉明重量为5时,有4 352种输入在经过M16后可全扩散,剩余16种输入均可扩散到15个位置.

性质6.输入向量的汉明重量大于5时,经过M16后均可全扩散.

根据上述6个性质可知,要使经过M16后全扩散,输入向量的汉明重量至少为2.则对于uBlock类结构,假定输入向量的汉明重量为1,则经过1轮轮函数后可扩散到11个位置,这11个位置经过2轮至多可扩散到16×5+11=91个位置,经过3轮至多可扩散到45×16+11=731个位置.因此,我们可以给出一系列uBlock类结构的全扩散轮数下界,如表4所示.表4显示了uBlock类结构具有极强的扩散性.

Table 4 Lower Bound of Full Diffusion Round for uBlock-like Structures

2.2 超级S盒

为了进一步估计算法抵抗差分和线性分析的能力，我们引入超级S盒的概念.uBlock类结构连续4轮轮函数作用在中间状态X上可以表示为

P∘T2∘M∘T1∘S∘P∘T2∘M∘T1∘S∘P∘T2∘

M∘T1∘S∘P∘T2∘M∘T1∘S(X).

(1)

注意到S和T1,T2,P可以交换位置，因此式(1)等价于

P∘T2∘S∘M∘S∘T1∘P∘T2∘M∘T1∘P∘T2∘

S∘M∘S∘T1∘P∘T2∘M∘T1(X),

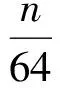
相应的Msuper=T1∘P∘T2∘M∘T1∘P∘T2为超级线性层.因此，可以通过Msuper的分支数来估计算法的活跃S盒数，进而估计其抵抗差分和线性分析的能力，即

Msuper=T1·P·T2·M·T1·P·T2=

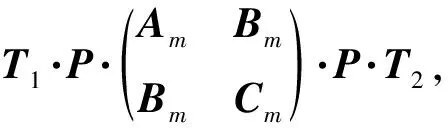
(2)

因此，我们可以直接通过式(2)来计算Msuper的分支数.

2.3 等价类划分准则

为了减少搜索空间，我们进一步探索uBlock类结构的等价类划分准则，并给出最优向量置换的搜索策略.首先，uBlock类结构可用图3描述：

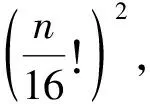
显然，图4(a)和4(b)两种形式是等价的，此时假若MQ=QM，则图4(c)与图4(a)和4(b)也是等价的，即可得到图4(d)与4(a)等价，即假若MQ=QM，则P与QPQ-1在uBlock类结构中具有相同的密码学性质.

于是，我们可以给出如下搜索策略：

策略1.uBlock类结构最优向量置换的搜索策略.

步骤1.确定使得MQ=QM的所有置换Q；

步骤2.对得到的所有置换Q，则P与QPQ-1属于同一个等价类.

步骤3.对每一个等价类中的代表元，测试算法整体的全扩散轮数.

步骤4.对全扩散轮数最小的置换，检测Msuper及其逆变换的分支数.

3 应 用

我们将第2节的搜索策略应用于128 b分组和256 b分组的uBlock类结构中，寻找最优向量置换.对于128 b和256 b分组的uBlock类结构，我们选择与uBlock算法中的结构相同，即P层是PL和PR的并置，且均为面向字节的向量置换，因此我们可以进一步优化搜索策略1.

3.1 128 b分组

128 b分组的uBlock类结构的扩散层描述如图5所示:

其中

则

其中，I为单位矩阵，O为零矩阵.

由表3可知，128 b分组的uBlock类结构至少需要2轮全扩散.因此，我们仅需要寻找2轮全扩散下的最优向量置换.出于性能的考虑，若PL或PR是恒等变换，则轮函数少一个指令，此时算法软件性能会有所提升.使用等价类划分技术，我们发现PL和PR是恒等变换时均有27个等价类满足2轮全扩散.部分具体实例在附录中给出.

此外，我们考虑4轮超级S盒下，扩散层的分支数达到最优的情形.由于

我们可将扩散层看作一个2×2的分块矩阵，考虑其为MDS矩阵，即分支数为3.此时，根据超级S盒和分支数的概念，可知其4轮至少有24个活跃S盒(与uBlock-128中选择的向量置换在4轮时的活跃S盒数一致).

Q1A2=A2Q1,Q2C2=C2Q2,

Q1B2=B2Q2,Q2B2=B2Q1.

策略2.uBlock-128最优向量置换的搜索策略.

步骤1.寻找使得Q3·A2=A2·Q3的所有置换Q3，记为集合SQ3；

步骤2.寻找使得Q4·C2=C2·Q4的所有置换Q4，记为集合SQ4；

步骤4.使用集合对SQ1,Q2中的置换，对P的全空间做等价类划分，若

则

步骤5.对每一个等价类中的代表元，输出4轮超级S盒下扩散层的分支数为3的置换P.

此时，当PL,PR其中一个为恒等置换时，不存在MDS矩阵.所以我们进一步将PL,PR其中一个放宽为循环移位，此时，满足2轮全扩散且超级扩散层为MDS时的等价类共有3 556个.部分具体实例在附录中给出.这一结果显示uBlock-128算法选择的向量置换是最优的，不存在可进一步减少指令数的最优向量置换对.受益于我们的等价类划分方法，最优向量置换对的数量大幅减少，这对后续进一步筛选满足其他安全性指标时提供了便利.

3.2 256 b分组

256 b分组的uBlock类结构的扩散层描述如图6所示.其中，

T1=(1,5,2,6,3,7,4,8),

T2=(1,3,5,7,2,4,6,8)，

我们首先关注256 b分组的uBlock类结构的全扩散轮数，得到定理1.

定理1.对于256 b分组的uBlock类结构，PL,PR选择基于字节的向量置换时，其全扩散轮数的下界为3.

证明.将256 b分组的uBlock类结构看作是8个分支的输入，从左到右依次是第1到第8个分支，每个分支都为8 b.我们假定输入向量汉明重量为1，为(0,1,0,…,0)，则经过一轮轮函数的输出为：

第1个分支为(a1,a2,a3,a4)，其中

a1=(0,0),a3=(0,1),a2=a4=(1,1).

第5个分支为(b1,b2,b3,b4)，其中

b1=b2=(1,1),b3=b4=(1,0).

其余分支的汉明重量均为零.注意到，(a1,a2,a3,a4)中的元素只能置换到下一轮M16输入的左半支，(b1,b2,b3,b4)中的元素只能置换到右半支.然而，要使2轮全扩散，进入下一轮4个M16的向量汉明重量只能为(2,2,3,4)和(2,3,3,3)，且汉明重量为2的部分只能有4种搭配，即(a1,b1),(a1,b2),(a3,b3)和(a3,b4).然而由第2节可知，对于M16，输入向量汉明重量为2时，只有8种情形可以全扩散，这8种情形左右半支汉明重量均为1，且非零位置只有(1,0)与(1,0)搭配和(0,1)与(0,1)搭配.因此，256 b分组的uBlock类结构至少需要3轮全扩散.

由表3可知，若256 b分组的uBlock类结构的P层使用更加细粒度的置换，则可能会在2轮达到全扩散.考虑到在算法实现时大置换实现效率不佳，因此我们并未尝试寻找大置换下2轮达到全扩散的情形.

接下来，我们试图寻找3轮全扩散下256 b分组的uBlock类结构的最优向量置换.对于PL和PR，我们与uBlock-256一样，考虑面向字节的向量置换.考虑到软件性能的提升，我们假定PL或PR其中一个为恒等变换，此时我们找到大量满足3轮全扩散的置换，在附录中我们给出了部分实例.

此外，我们考虑4轮超级S盒下，扩散层的分支数为4的情形.由于

我们可将扩散层看作一个4×4的分块矩阵，考虑其分支数为4的情形.此时，根据超级S盒和分支数的概念，可知其4轮至少有32个活跃S盒(与uBlock-256算法中的置换在4轮时的活跃S盒一致).

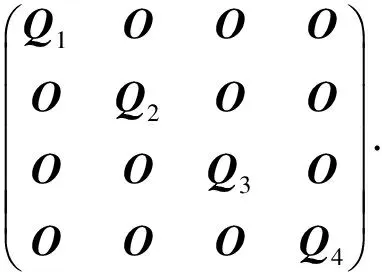
Q1A2=A2Q1,Q2A2=A2Q2,

Q3C2=C2Q3,Q4C2=C2Q4,

Q1B2=B2Q3,Q2B2=B2Q4,

Q3B2=B2Q1,Q4B2=B2Q2.

因此，我们给出如下搜索策略3:

策略3.uBlock-256最优向量置换的搜索策略.

步骤1.寻找使得Q3·A2=A2·Q3的所有置换Q3，记为集合SQ3；寻找使得Q4·C2=C2·Q4的所有置换Q4，记为集合SQ4.

步骤2.寻找集合对SQa,Qb，使得Qa∈SQ3,Qb∈SQ4满足Qa·B2=B2·Qb；寻找集合对SQc,Qd，使得Qc∈SQ3,Qd∈SQ4满足Qd·B2=B2·Qc.

步骤3.取(Q1,Q2)∈SQa,Qb,(Q3,Q4)∈SQc,Qd,对P的全空间做等价类划分，即若

步骤4.对每一个等价类中的代表元，输出3轮全扩散且4轮超级S盒下扩散层的分支数为4的置换P.

经过实验，当PL和PR其中一个为恒等变换时，我们并未找到3轮全扩散且在4轮超级扩散层分支数为4的置换对.对于PL和PR均为一般置换时，存在大量3轮全扩散且在4轮超级扩散层分支数为4的置换对，部分具体实例在附录中给出.

在仅考虑全扩散轮数、性能和超级扩散层的分支数这3个指标时，我们的结果与uBlock-256使用的向量置换是一致的.然而，本文中给出的等价类划分规则可以将满足条件的置换对缩小到较小的范围，这将为后续进一步测评其抵抗其他分析方法时提供便利.

4 总 结

在本文中，我们探索uBlock类结构最优向量置换的选取.对于uBlock算法族，扩散层分为2部分：一部分是由Feistel结构构造的16维最优二元扩散层，另一部分为2个向量置换的并置.我们的目标是在二元扩散层固定的前提下，寻找最优向量置换来提升算法整体的安全性和实现效率.本文中，我们主要的评价指标为算法的全扩散轮数、软件性能和4轮超级S盒下扩散层的分支数.

首先，我们探索uBlock类结构的扩散性，给出了不同规模下uBlock类结构全扩散轮数的下界.其次，为了减少搜索复杂度，基于uBlock类结构的特点，我们提出了等价类划分技术.进一步，基于全扩散轮数最优、软件性能优良和超级扩散层的分支数，我们设计了uBlock类结构最优向量置换的搜索策略.最后，将搜索策略应用于128 b和256 b分组的uBlock类结构中.在具体应用时，结合不同分组长度下算法的特点，我们进一步优化了最优向量置换的搜索策略，并给出具体实例.

对于128 b分组的uBlock类结构，若PL和PR其中一个为恒等变换时，存在满足2轮全扩散的置换对；然而，不存在2轮全扩散且超级扩散层分支数最优的置换对.因此，我们将PL或PR放宽到循环移位后，给出了全扩散轮数及超级扩散层分支数均最优的置换对.对于256 b分组的uBlock类结构，我们证明了其最优全扩散轮数为3轮，若PL或PR其中一个为恒等变换时，存在3轮全扩散的置换对，然而不存在全扩散轮数为3且超级扩散层的分支数为4的置换对.与uBlock算法相比，在仅考虑全扩散轮数这一指标时，算法所需的向量置换指令更少，从而有更高的软件实现效率.在考虑全扩散轮数和超级扩散层分支数2个指标后，我们的结果与uBlock算法中使用的向量置换是一致的，表明uBlock算法选择的向量置换是最优的，不存在可进一步减少指令数的向量置换对，但是我们提出的等价类划分规则可以将置换对的数量大幅减少，为后续uBlock类算法的设计提供技术支持.

作者贡献申明：李晓丹提出了算法思路，撰写论文；吴文玲提出指导意见并修改论文；张丽提出修改意见.