效用优化的本地差分隐私集合数据频率估计机制

2022-10-14 06:02:22曹依然朱友文贺星宇

计算机研究与发展 2022年10期

曹依然朱友文,2 贺星宇张跃

1(南京航空航天大学计算机科学与技术学院南京 211106) 2(广西可信软件重点实验室(桂林电子科技大学) 广西桂林 541004)

随着经济科技的飞速发展和信息技术的普及应用，人们时时刻刻都在不断地产生大量的数据信息.作为一种重要的数据形式，集合数据在日常生活中有着广泛的应用场景，如购买过的物品、近期到过的地点等，都可以表示为集合数据.通过对这些数据进行收集、记录和分析，可以挖掘出它们中的隐藏信息，对学术、工业、社会服务等多个领域都有重要意义.例如通过分析用户的购买记录，可以得出用户购买需求，从而提高交易成功率；通过分析车联网系统中的GPS数据，可以得出实时路况和拥堵情况，从而提供交通流量控制服务.但这些数据中往往包含着大量隐私信息，如购物数据会反映个人生活习惯和财务状况、轨迹数据会包含家庭和工作地址，如果直接将这些数据提供给其他人使用，不仅会对个人的人身安全、财产安全造成极大的威胁，也会使得用户不再愿意共享数据.目前，区块链[1]、边缘计算[2]、机器学习[3-4]等领域已经关注到了隐私保护问题的重要性，并针对特定问题提出了隐私保护的解决方案.然而，如何在保护用户隐私的前提下对数据进行收集，仍是学术界亟待解决的问题.

当今，针对隐私保护，主要的解决方案可以分为3类：匿名化技术[5-6]、密码学技术[7-8]，以及差分隐私[9-10].差分隐私拥有严格的形式化安全模型，并具有高效低开销的特点，是当今研究的热点方向.作为差分隐私的一大变种，本地差分隐私(local differential privacy, LDP)[11]在继承了差分隐私优点的基础上，摒弃了对可信第三方的需求，大大提高了模型的实用性.自从2013年被正式提出至今，本地差分隐私技术已经有了长足的发展与改进，其应用场景也十分宽泛，如机器学习[12-13]、网络服务[14]、数据的统计与优化[15-17]，等等.同时，本地差分隐私也已经广泛部署到工业界实际应用中，苹果公司将其应用到手机上来保护用户的使用数据[18-19]，谷歌公司也设计了基于本地差分隐私的组件RAPPOR[20]来采集用户行为数据.

但是，现有的本地差分隐私机制大多并未考虑到，针对实际应用中不同数据的隐私保护需求差异，可以通过降低对非敏感数据的保护程度来减小估计误差.为此，Murakami等人提出了效用优化本地差分隐私(utility-optimized local differential privacy, ULDP)模型[21]，通过对不同的数据处以不同的扰动方法，从而在保障敏感数据隐私安全的前提下提高数据效用.然而，ULDP模型仅仅可以处理用户数据均为敏感值或均为非敏感值的情况，当用户数据为集合数据，并且既包含敏感值又包含非敏感值时，ULDP模型难以直接适用.在很多现实应用中，用户的集合数据会同时包含敏感值和非敏感值，比如，一位用户的购物订单记录为{梳子，洗发水，卫生纸，胃药}，此时梳子、卫生纸和洗发水是非敏感值，而胃药则是敏感值，ULDP模型无法直接处理该类数据.因此，需要提出一种新的模型，来处理用户数据且既包含敏感值又包含非敏感值的情况，保证在不降低对敏感数据保护效果的前提下，提高频率估计结果准确度.

本文首先定义了针对集合数据的效用优化本地差分隐私模型，该模型是ULDP模型在集合数据上的理论拓展，可以处理用户数据且既包含敏感值又包含非敏感值的情况，具有更广泛的适用性.随后，本文基于集合数据效用优化本地差分隐私(set-valued data utility-optimized local differential privacy, SULDP)模型提出了5种频率估计机制，并通过理论分析证明了所提出的5种机制能够对敏感数据实现与现有的本地差分隐私机制完全相同的保护效果，同时通过降低对非敏感数据的保护效果，提高频率估计结果的准确度.最后，本文在多个真实数据集和模拟数据集上展开了实验，结果表明本文所提机制可以有效降低估计误差，提升整体数据效用.

概括地说，本文的主要贡献包括3个方面:

1)定义了SULDP模型;

2)基于传统频率估计机制，本文提出了符合SULDP模型的5种频率估计机制suGRR,suGRR-Sample,suRAP,suRAP-Sample和suWheel;

3)通过理论分析和实验对比了提出的5种机制，证明了这5种机制相较于原始机制均在效用方面有所提升，其中suWheel机制表现最优.

1 相关工作

针对用户集合数据进行的统计分析在推荐系统等领域都有着重要的研究意义，直观地，我们可以将针对类别数据的方法应用到集合数据的每一个条目上，但同时为了满足差分隐私的定义，还需要根据条目数量对隐私预算进行划分，当数量较大时，会导致数据效用急剧降低.

文献[22]基于RAPPOR实现了集合数据频率估计，虽然比直接划分隐私预算的效果要好，但是在进行扰动时仍然需要将隐私预算除以集合数据条数，集合变大时数据效用仍然很低，并且通信代价也很高.文献[23]提出了PrivSet机制，它是基于指数机制实现的，输出域为数据域的大小固定为k的所有子集，根据与输入集合是否相交来确定各个子集的输出概率，数据效用相较于文献[22]有所提升，但是k的最优取值是需要根据理论分析的均方误差(MSE)来确定的，由于分析结果非常复杂，无法直接计算出最优的k，只能通过顺序查找来找到，当数据域较大时就会造成很高的计算代价.文献[24]提出了Wheel机制，这也是目前效果最好的集合数据频率估计机制.Wheel机制通过哈希将原始集合数据映射到[0,1)上，然后以一定的概率密度从[0,1)上取值作为输出，Wheel机制的通信代价比RAPPOR和PrivSet都要低，并且文献[24]还证明了Wheel机制的MSE达到了集合数据频率估计MSE的理论最优下界.但是Wheel等机制都是在LDP的定义下实现的，LDP模型为所有用户和所有输入提供同等的隐私保护.

文献[21]将输入域分为敏感数据和非敏感数据，在保证敏感数据的不可区分性的前提下，以一定的概率降低对非敏感数据的保护效果，提高了整体的数据效用.类似的机制还有文献[25-26]提出的个性化本地差分隐私，为用户提供了个性化的隐私需求，但并未考虑到数据层面.而文献[27]提出的地理位置不可区分性则主要根据不同数据之间的距离来确定它们输出同一结果的概率，距离越近则概率越大，这也可以在一定程度上提高数据效用，但是由于距离度量需要满足三角不等式，因此针对某些数据类型是不适用的.

但是ULDP是基于类别数据提出的，如果想直接应用到集合数据就需要划分隐私预算，这会对数据效用产生极大的影响.综上，现有方法均存在不足之处，本文针对集合数据的效用优化频率估计机制进行了研究.

2 背景知识

2.1 本地差分隐私

在本地差分隐私中，由用户自己在本地对数据进行扰动，然后将扰动后的数据发送给服务器，服务器再利用这些数据计算得到所需的统计信息.由于服务器无法接触到用户的原始数据，因而无法获得用户的隐私信息.本地差分隐私的形式化定义如下.

定义1.ε-LDP[11].给定隐私预算ε≥0，对输入域为X、输出域为Y的扰动机制M:X→Y，该扰动机制M满足ε-LDP，当且仅当对于任意输入x,x′∈X，得到任意输出y∈Y的概率满足

M(y|x)≤eεM(y|x′).

(1)

不难看出，ε-LDP保证了任意攻击者无法从输出结果推断出确切的原始输入，并且当隐私预算ε趋近于0时，X中所有数据都以几乎相同的概率输出同一结果，即隐私预算ε越小，对用户隐私保护程度越强.

2.2 效用优化本地差分隐私

LDP并未考虑用户不同数据的敏感度差异，如统计用户身体状况时，对于“癌症”和“感冒”都使用了同样的扰动方法，这会使得对一些非敏感数据“感冒”保护效果过强，使得数据效用减弱.效用优化本地差分隐私就是针对这一问题进行了改进.ULDP将原始数据集X划分成敏感数据集Xsen和非敏感数据集Xnon,将输出集划分为保护数据集Ypro和可逆数据集Yinv，它的形式化定义如下.

定义2.(Xsen,Ypro,ε)-ULDP[21].给定Xsen⊆X，Ypro⊆Y，ε≥0，对输入域为X、输出域为Y的扰动机制M:X→Y，当且仅当扰动机制M满足以下性质时，M满足(Xsen,Ypro,ε)-ULDP.

1)对于任意y∈Yinv，有且仅有一个x∈Xnon，

M(y|x)>0,

(2)

且对于任意x≠x′，有

M(y|x′)=0.

(3)

2)对于任意输入x,x′∈X，得到任意给定输出y∈Ypro的概率满足

M(y|x)≤eεM(y|x′).

(4)

2.3 现有的频率估计机制

我们介绍了3种常见的本地差分隐私频率估计机制GRR(generalized randomized response)机制、RAPPOR机制和Wheel机制的扰动过程.这3种机制均可应用于保护隐私的集合数据频率估计，然而都难以应对集合数据中同时包含敏感值和非敏感值的情况.

2.3.1 GRR机制

在GRR机制[28]中，输出域与输入域相同，即X=Y，给定ε≥0，则GRR以表达式(5)所示的概率将x扰动成y，

(5)

式(5)表示了GRR处理类别数据的方式，若要处理集合数据，则需要先对数据进行抽样，将其转化为类别数据，或者根据集合数据条数划分隐私预算，再对集合中每条数据分别处理.

2.3.2 RAPPOR机制

RAPPOR机制[20]需要先对原始数据进行编码，通过独热编码将x映射为向量c，然后再对c进行扰动，当用户数据为类别数据时，c中只有1位为1，这一位以p=eε/2/(eε/2+1)的概率保持不变，其余为0的位则以q=1/(eε/2+1)的概率反转为1.

随后工作[22]又对RAPPOR进行了改进，使之可以处理集合数据.设每个用户有m条数据，则编码后的向量c中有m个1，为了满足ε-LDP，这些位保持不变的概率为

(6)

相应地，为0的位反转为1的概率为

(7)

此外，与GRR类似，RAPPOR也可以直接从集合中抽样出一条数据，然后直接使用原始的RAPPOR进行处理.

2.3.3 Wheel机制

Wheel机制[24]是由Wang等人在2020年提出的用于集合数据频率估计的机制，具有通信代价低、估计误差小的优点.Wheel机制用户端的扰动过程主要分为2步：第1步是将x通过哈希函数映射到v∈[0,1)，第2步则是根据式(8)所示的概率密度得到扰动结果y

(8)

其中v={v1,v2,…,vm}是用户数据哈希后的结果；Cv={t|t∈[vi,vi+p)或[0,vi+p-1),i∈{1,2,…,m}}表示总体覆盖区域；参数p=1/(2m-1+meε)表示覆盖长度；l是Cv的长度，即总覆盖长度；参数Ω=mpeε+1-mp则是正则化因子.注意扰动结果y∈[0,1)，也就是输出域是[0,1).

3 针对集合数据的效用优化本地差分隐私模型

3.1 符号描述

本文中所用到的主要符号描述如表1所示：

Table 1 Notations Description

3.2 效用优化本地差分隐私模型的建立

ULDP模型虽然就数据敏感性问题进行了研究，但是仅能处理用户输入均为敏感值或均为非敏感值的情况.当用户集合数据中既包含敏感值，又包含非敏感值时，ULDP模型就无法直接处理了.例如统计用户购物数据时，假设某一位用户的购物记录为{香蕉，牛奶，洗衣液，心脏病药物}，此时心脏病药物为敏感值而其他数据则为非敏感值，ULDP模型就难以直接适用了.因此我们提出了SULDP模型，通过降低对集合中非敏感数据的保护效果，来提高统计结果的准确性.这里我们首先给出SULDP的形式化定义.

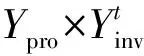
1)对于任意yi∈Yinv，其中1≤i≤t，有且仅有一个x∈Xnon可以映射到yi，即

当x∈s时，

M(yi|s)>0,

(9)

当x∉s时，

M(yi|s)=0.

(10)

2)对于任意输入集合s,s′⊆X，得到任意输出y0∈Ypro的概率满足

M(y0|s)≤eεM(y0|s′).

(11)

在定义3中，式(11)保证了对敏感值的保护程度不会降低；式(9)和式(10)则对应非敏感值，允许通过降低对其保护效果来提高统计结果的准确性.同时，如果限定每个输入集合大小为1时，即|s|=1，那么SULDP将退化到ULDP模型.因此，ULDP模型是我们SULDP模型的一种特殊情况.SULDP模型是ULDP模型在集合数据上的理论拓展，具有更广泛的适用性.

3.3 问题定义

本文专注于在保证用户敏感数据保护效果的前提下，提升频率估计结果准确性.我们考虑的系统模型中包含n个用户和1个服务器.其中，每个用户i持有一个私有的集合si={x1,x2,…,xm}，s⊆X，即X为原始数据的全集，令|X|=d.我们假设X中既包含敏感值，又包含非敏感值，所有敏感值构成的集合记为Xsen，所有非敏感值构成的集合记为Xnon，Xsen∪Xnon=X.

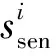
定义3中我们假设用户手中数据条数是一定的，但通过简单扩展可以处理用户手中数据条数不同的情况.即通过填充采样[29]的方式，将用户数据条数统一为m.具体扩展方式为：首先由服务器根据前期调研或实际情况指定m.然后由用户在本地对自己数据进行预处理.若数据条数小于m，则使用虚假数据补齐到m条；若数据条数大于m，则从中随机抽取m条，然后再对数据进行后续处理.

3.4 效用评价标准

本文采用MSE对机制的效用进行评估.MSE表达式为

(12)

4 机制设计及理论分析

4.1 基于GRR的机制设计

4.1.1 方案描述

我们首先基于GRR提出满足SULDP模型的suGRR(set-valued utility-optimized GRR)机制.在suGRR中，保护数据域Ypro是敏感数据域Xsen子集构成的集合，可逆数据域Yinv与非敏感数据域Xnon相等，令p=eε/m/(eε/m+|Xsen|-1),q=1/(eε/m+|Xsen|-1)，r=(eε/m-1)/(eε/m+|Xsen|-1)，给定集合数据s，则suGRR以表达式(13)所示的概率对s中每一条数据x进行扰动，然后将属于Xsen的输出z看作一个集合，即为suGRR输出部分的y0，余下属于Xnon的输出z则分别对应y1,y2,…,yt，

(13)

相应地，当服务器收到用户发来的数据后，首先需要对X中所有数据出现的次数进行统计，设x出现次数为Fx，然后再以表达式(14)所示的方法计算出其频率估计值，

(14)

(15)

4.1.2 理论分析

定理1.suGRR和suGRR-Sample均符合SULDP模型.

证明.suGRR中，对任意y∈Yinv，有且仅有一个x∈Xnon可扰动至该可逆数据，即当且仅当x∈s时，以r的概率输出该可逆数据，因此满足SULDP定义中式(9)、式(10)所规定的第1条性质.

对于任意s,s′⊆X，输出同一结果y0的概率为

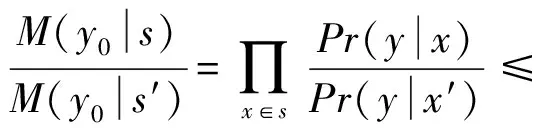
因此满足式(11)所规定的第2条性质.

综上，suGRR符合SULDP模型，同理，我们也可以证明suGRR-Sample符合SULDP模型.

证毕.

定理2.suGRR和suGRR-Sample频率估计结果均为无偏估计.

证明.在suGRR中，x∈Xsen时，Fx可以看作是nf(x)个成功概率为p和n(m-f(x))个成功概率为q的伯努利变量之和，因此，

x∈Xnon时，由扰动过程可知

因此，suGRR的频率估计结果为无偏估计，同理，suGRR-Sample的频率估计结果也是无偏估计.

证毕.

定理3.suGRR的MSE表达式如式(16)：

(16)

suGRR-Sample的MSE表达式如式(17)：

(17)

证明.由定理2可得，式(14)为无偏估计，因此MSE就等于方差，当x∈Xsen时，

当x∈Xnon时，

将p,q,r带入，即可得到式(16).同理，也可以证明suGRR-Sample的MSE表达式为式(17).

证毕.

4.2 基于RAPPOR的机制设计

4.2.1 方案描述

基于GRR的扰动过程虽然简单、易于实现，但是当数据域很大时，p,q,r会趋向于0，会使得数据扰动概率过大，数据效用降低，而RAPPOR则不会受此影响.因此，基于RAPPOR，我们提出满足SULDP模型的suRAP(set-valued utility-optimized RAPPOR)机制.

在suRAP中，首先会对数据进行独热编码，即将用户手中的集合数据s编码为一个d比特的向量a，每一位都与原始数据域中的一条数据相对应，若s中包含有xi，则令a的第i位为1，即a中有m个1，其余位为0.

不失一般性，我们假设{x1,x2,…,x|Xsen|}为敏感数据Xsen，{x|Xsen|+1,x|Xsen|+2,…,x|X|}为非敏感数据Xnon，则Ypro={(y1,y2,…,y|X|)|y1,y2,…,y|X|∈{0,1}}，Yinv=Xnon.令p=eε/2m/(eε/2m+1),q=1/(eε/2m+1)，r=(eε/2m-1)/eε/2m，则suRAP以表达式(18)所示的概率对a中每一位ai进行扰动得到bi，

(18)

则y0就等于向量b，同时，若xi∈Xnon且bi=1，则表示输出了可逆数据xi，即我们可以直接使用b来表示(y0,y1,…,yt),t≤|snon|.

服务器端收到用户发来的数据后，首先需要对b中所有位出现1的次数进行统计，设x对应位出现1的次数为Fx，则其估计频率为

(19)

类似地，为了避免划分隐私预算ε，我们也基于采样提出了suRAP-Sample，此时p=eε/2/(eε/2+1)，q=1/(eε/2+1)，r=(eε/2-1)/eε/2，用户从s中随机抽取一条数据并编码为a，注意这时a中只有一位为1，然后同样使用式(18)进行扰动并提交结果给服务器，服务器统计出x对应位出现1的次数Fx后，即可根据式(20)计算出x的估计频率，

(20)

4.2.2 理论分析

定理4.suRAP和suRAP-Sample均符合SULDP模型.

证明.suRAP中，对于任意s,s′⊆X，输出同一结果y0的概率为

因此满足式(11)所规定的第2条性质.

对任意y∈Yinv，有且仅有一个x∈Xnon可扰动至该可逆数据，即当且仅当x∈s时，以r的概率输出该可逆数据，因此满足SULDP定义中式(9)、式(10)所规定的第1条性质.

综上，suRAP符合SULDP模型，同理，我们也可以证明suRAP-Sample符合SULDP模型.

证毕.

定理5.suRAP和suRAP-Sample频率估计结果均为无偏估计.

证明.当x∈Xsen时，有

x∈Xnon时，由扰动过程可知：

综上，suRAP的频率估计结果为无偏估计，同理，suRAP-Sample的频率估计结果也是无偏估计.

证毕.

定理6.suRAP的MSE表达式如式(21)：

(21)

suRAP-Sample的MSE表达式如式(22)：

(22)

证明.与定理3证明过程类似.

4.3 基于Wheel的机制设计

4.3.1 方案描述

虽然基于RAPPOR处理集合数据相较于基于GRR的效果有所提升，但是其通信代价很高，并且效果也并非目前最优的，因此我们在本节提出满足SULDP模型的suWheel(set-valued utility-optimized wheel)，具体的扰动算法如算法1所示.

算法1.suWheel用户端扰动算法.

输入：集合数据s={x1,x2,…,xm}、敏感数据域Xsen、非敏感数据域Xnon、隐私预算ε、用户数据条数m、覆盖长度p=1/(2m-1+meε)、正则化因子Ω=mpeε+1-mp、哈希函数h:X→[0.0,1.0)；

输出：三元组z=〈z0,z1,h〉，其中z0=y0表示保护数据，z1={y1,y2,…,yt}(t≤|snon|)表示可逆数据，h为该用户使用的哈希函数.

①v={h(x1),h(x2),…,h(xm)}={v1,v2,…,vm}；/*将原始数据映射到[0.0,1.0)上*/

②Cv={t|t∈[vi,vi+p)或[0,vi+p-1),i∈{1,2,…,m}}；

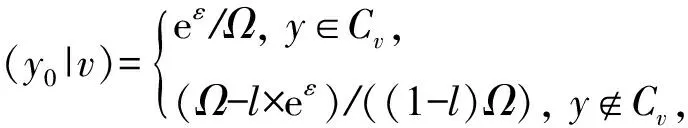
以Q(y0|v)所示概率密度得到扰动结果y0，其中l是Cv的长度，令z0=y0；

④z1=∅；

⑤ fori=1 tom:

⑥ ifxi∈Xnon:

⑦ ify0∉[vi,vi+p)且[0,vi+p-1)

⑧ addxiintoz1；

⑨ end if

⑩ end if

其中z0对应的是y0，z1则对应yi(1≤i≤t).令Cvx为元素x对应的覆盖区域，当x∈s时，输出的z0属于该区域的概率为Ptrue=peε/(mpeε+1-mp)，当x∉s时，概率则为Pfalse=p.

算法2.suWheel服务器端聚合算法.

①Fx=0；

② ifx∈Xsen

③ fori=1 ton

④v=hi(x)；

⑥Fx=Fx+1；

⑦ end if

⑧ end for

⑩ end if

4.3.2 理论分析

定理7.suWheel符合SULDP模型.

证明.suWheel中，对任意y∈Yinv，有且仅有一个x∈Xnon可扰动至该可逆数据，即当且仅当x∈s时，以r=1-eεp/Ω的概率输出该可逆数据，因此满足SULDP定义中式(9)、式(10)所规定的第1条性质.

对于任意集合s,s′⊆X，输出同一结果y0的概率为

令

(23)

(24)

化简得l(eε-1)≤mp(eε-1)，因为l为覆盖区域的总长度，并且各个元素覆盖区域之间可能会存在相交的情况，因此l≤mp，又有ε≥0，所以式(24)恒成立.即满足SULDP定义中式(11)所规定的第2条性质.

综上，suWheel符合SULDP模型.

证毕.

定理8.suWheel频率估计结果为无偏估计.

证明.当x∈Xsen时，Fx可以看作是nf(x)个成功概率为Ptrue和n(1-f(x))个成功概率为Pfalse的伯努利变量之和，因此

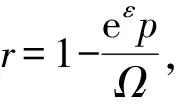
综上，suWheel的频率估计结果为无偏估计.

证毕.

定理9.当ε=O(1)时，suWheel的MSE表达式如式(25)：

(25)

证毕.

4.4 理论结果对比

我们首先对suGRR，suGRR-Sample，suRAP，suRAP-Sample，suWheel等5种机制的效用进行评估.因为

根据定理3、定理6和定理9，我们可以计算得到ε=O(1)时本文机制与现有本地差分隐私机制分别所对应的MSE，结果如表2所示.

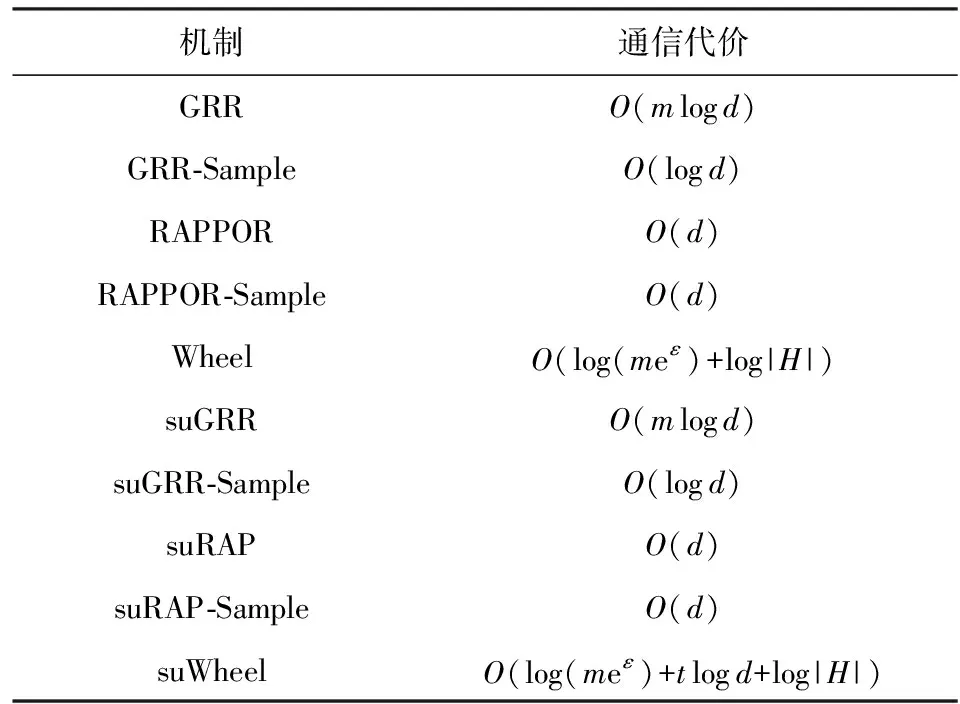
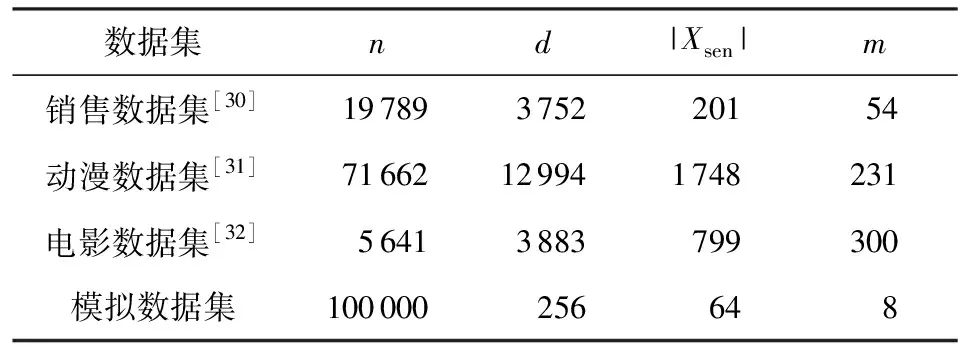
f(Xnon)表示非敏感数据的真实频率总和，因此MSE的前半部分，即敏感数据造成的误差在实际应用中占主导地位.而在实际应用中，敏感数据在总体数据中的占比往往很小，即|Xsen|

Table 2 Comparison of MSE when ε=O(1)

除了数据效用，通信代价也是评价一个机制好坏与否的重要标准，假设suWheel中使用的哈希函数是从集合H中选取的，表3给出了相应的结果.可以看出suWheel虽然比suGRR-Sample略高，但是仍然是可以接受的.

Table 3 Comparison of Comunication Cost

5 实验

5.1 实验设置

我们的实验环境设置如下：操作系统为Windows 10，处理器为Inter i7-6700 CPU，内存为32 GB，实验所用的语言为Python 3.6.

我们在4个数据集上进行了实验，表4展示了它们的参数信息.销售数据集[30]包含了英国一家商店一年的在线交易信息，该商店主要销售成人、儿童和家居用品，我们将敏感数据设置为儿童用品；动漫数据集[31]则描述了用户对一些动漫的评分，我们将每位用户评分的动漫作为一条集合数据，并将类别为成人、惊悚、恐怖的动漫作为敏感数据；对电影数据集[32]也是类似的处理.

Table 4 Description of Dataset Parameters

我们是将常规意义上可能会泄露用户隐私的数据设置为敏感值.比如销售数据集中儿童用品会泄露用户孩子的性别和年龄；动漫数据集和电影数据集中给成人、惊悚等类别的动漫、电影评价的信息则会泄露用户的观影偏好，而针对此类特殊类别的影视的喜好信息对于用户而言往往也是较为敏感的.在实际应用中，针对敏感值和非敏感值的划分，可以由服务器根据常识和专业知识决定，同时根据用户的使用反馈来进行补充，也可以通过问卷调查等调研方式收集各个用户认为的敏感数据，然后由服务器取并集作为敏感值划分结果.

此外，我们所使用的3个真实数据集都是不定长的，因此需要对它们进行预处理，通过填充采样的方法将之转换为定长数据.同时，我们还使用蓄水池抽样的方法生成了模拟数据集.

实验采用MSE作为评估标准，用以评价频率估计准确性.同时，为避免随机性影响实验结果,本文中每一项实验重复进行10次,并取平均值作为结果.

5.2 实验结果

5.2.1ε对MSE的影响

本节对比了5种机制在不同隐私预算ε下的性能差异，实验结果如图1所示.可以看出，随着隐私预算ε的增大，5种机制的MSE都在减小，相应地，频率估计结果会更加准确，数据效用也就越高.即ε越大，隐私保护程度越低，MSE越小，数据效用越高.

同时，基于GRR的2个机制的效用要明显低于另外3个，这是因为实验中数据域都很大，suGRR和suGRR-Sample中数据被扰动的概率会很大，频率估计效果就会很差，这也与GRR的特性一致.

除此之外，文献[21]提出了基于ULDP的uRR和uRAP机制，并建议通过划分隐私预算来实现对集合元素的频率估计需求，划分隐私预算的uRR实际上就等同于本文所提出的suRR，而suRAP则是基于改进的RAPPOR[22]实现的，效果比划分隐私预算的uRAP要更好.因此，无论是与本文所提出的4种机制比较，还是与文献[21]比较，suWheel都是表现最优的机制.

5.2.2 |Xsen|对MSE的影响

本节通过随机抽样的方法选取敏感数据，来调整敏感数据域在全体数据域中的占比，进而评估|Xsen|对MSE的影响.我们将隐私预算ε固定为1，结果如图2所示.可以看出，随着|Xsen|的增大，5种机制的MSE都会增大，即敏感数据越多，需要的扰动就越多，估计结果的准确度就越低，数据的整体效用就会越差.

此外，当|Xsen|/|X|=1，即用户数据均为敏感值时，等同于直接使用原始的GRR，RAPPOR等机制进行处理，此时效果是最差的.这也证明了通过对数据进行划分，然后根据敏感与否加以不同的处理方式，确实可以在一定程度提高整体数据效用.

5.2.3d对MSE的影响

数据域大小d也对数据效用有一定的影响.由于真实数据集的数据域是固定的，因此本节通过不同大小的模拟数据集来进行评估.实验设置的d的取值范围为{16,32,64,…,1 024}，并且敏感数据占比为0.25，隐私预算ε=1，m=8，结果如图3所示:

根据实验结果来看，随着d的增大，suGRR和suGRR-Sample的MSE呈现不变的趋势，这是因为基于GRR的2种方法的敏感数据部分的MSE与|Xsen|2正相关，这使得2方面的影响相互抵消了.而其余3种则是与|Xsen|成正相关，因此前者的影响占了主导地位，MSE呈下降趋势.

5.2.4m对MSE的影响

本节则主要评估了m对MSE的影响，同样是通过构造不同模拟数据集来进行实验.令敏感数据占比为0.25，隐私预算ε=1，数据域大小d=256，设置m的取值范围为{1,2,4,8,…,64}.

与5.2.3节的分析类似，m对MSE的影响也包括2方面：1)其余参数一定，m越大，每条数据对应的真实频率就越低，相应的MSE也就越大；2)如4.4节所示，suWheel的敏感部分的MSE与m呈正相关，其余4种机制更是与m2呈正相关，因此m越大，MSE也越大.

实验结果如图4所示，随着m的增大，5种机制的数据效用都会变低，并且suWheel的MSE增大的幅度要明显小于另外4个机制.

6 结论

现有本地差分隐私集合数据频率估计机制在设计时并未考虑数据的敏感性差异，本文针对这一问题，首先定义了针对集合数据的效用优化本地差分隐私模型，并提出了符合SULDP模型的suGRR，suGRR-Sample，suRAP，suRAP-Sample和suWheel机制，在保证敏感数据隐私保护效果不降低的前提下，提高了整体的数据效用.从理论和实验的结果来看，suWheel具有低通信代价和高数据效用的特点，是整体表现最优的机制.

未来的工作包括2个方面：1)研究使用本文所提的思想，对本地差分隐私下的其他机制，如均值估计机制等进行改进；2)当前工作只是将数据分为了敏感和非敏感2种类型，那么可以通过对敏感程度进一步细分来达到更高的数据效用.

作者贡献声明：曹依然负责完成实验并撰写论文；朱友文提出了算法思路和实验方案；贺星宇和张跃协助设计了实验方案和对比分析.