雾辅助物联网中公平节能的计算迁移

陈思光，尤子慧

1) 南京邮电大学江苏省宽带无线通信和物联网重点实验室，南京 210003

2) 南京邮电大学江苏省通信与网络技术工程研究中心，南京 210003

随着5G 技术的不断推进和发展，智能感知设备也将保持高速增长的趋势[1]，主要包括智慧医疗设备[2]、车载感知设备、工业控制设备[3]、智能家居设备、智能电表[4-5]以及智能手机等.为了实现人、机、物的互联互通，物联网(Internet of things，IoT)应运而生，它将智能设备与互联网结合起来，进行信息交换与通信[6-7].由于本地设备的计算资源和计算能力有限，难以承担大规模密集型任务的处理，因此传统物联网一般利用云服务器为各种物联网应用提供支持[8].然而，随着物联网中海量数据的生成，云计算中的带宽消耗和数据处理负担愈加沉重，任务处理过程将面临高延迟、高能耗以及网络拥塞等各种问题.

为了应对云计算中的这些挑战，2012 年，思科提出了雾计算[9-11]的概念.相比于云计算，雾计算更接近终端设备，数据处理时延低，移动性强，能够有效降低核心网络压力，减少能耗.在此基础上，为了进一步提高任务处理效率，缓解本地设备的资源约束问题，计算迁移理论也受到了学者们的广泛关注，其中，基于雾计算的计算迁移[12-13]作为一种解决物联网中大数据处理问题的有效方法，近年来受到学界与业界的特别关注.在雾计算环境下，物联网设备可以将计算任务迁移至附近的雾节点进行处理，能够有效缓解物联网设备的计算压力，提高任务处理速度.目前，在基于雾计算的计算迁移方案中，能源消耗以及时延问题一直备受关注.在时延方面，在文献[14]中，Chen 等设计了一种完成时间最小化的迁移机制，该机制联合优化了雾辅助物联网的计算资源分配和迁移决策.文献[15]在车辆雾计算系统中，将802.11p作为车辆之间通信的传输协议，以最大程度提高系统的长期收益（主要考虑延迟、资源与任务多样性）为目的，提出了一种最优任务迁移方案，能够为一些延迟敏感的应用提供服务.而在能耗方面，文献[16]提出了一种雾辅助物联网中隐私和能量协同感知的数据聚合计算迁移方案，在有效解决物联网设备计算受限问题的同时，在数据处理和转发过程之中提供安全保障.

当前，也有许多学者基于能耗与延迟的联合优化，构建了一系列解决方案，例如，文献[17]研究了具有不同计算能力的异构雾节点所组成的雾计算网络中的任务迁移方案，提出了一种最小化每个终端用户的任务处理总延迟和能耗的加权和的迁移策略.文献[18]，针对混合能源供应的无线接入雾计算网络提出一种延迟感知的节能计算迁移方案，能够有效降低电网功耗.为了解决一些延迟敏感的计算密集型任务所带来的挑战，文献[19]提出了一种基于深度学习的联合迁移决策和资源分配算法，该算法通过联合优化迁移动作、带宽、本地和外部CPU 的占用率来解决任务完成时间和能量消耗加权和的最小化问题.文献[20]研究了一种能量约束的能量收集任务迁移方案，使得能耗和时延的加权和最小.然而，上述任务迁移方案虽然能够在能耗以及时延方面表现不错，但都缺乏对雾节点能耗公平性的考量，这极有可能导致接近终端设备的雾节点或是处理能力高、计算资源丰富的雾节点负担沉重.

在雾辅助物联网中，雾节点可以大致分为电网供电雾节点和电池供电雾节点两类，雾节点可能是处理能力强，且有电网供电的边缘服务器，也有可能是电池供电的网络节点，如空闲状态的智能手机等.而对于电池供电的雾节点来说，电池寿命是至关重要的[21].因此，若在追求计算迁移方案中最小化能耗和时延的同时，能够关注异构雾节点各自的处理能力及可持续性的不同，加强对雾节点能耗公平性的考量，就可以达到网络寿命最大化的目的.在目前的研究中，文献[22]提出了一种两步公平任务迁移方案，该方案根据公平性度量选择迁移的雾节点，然后根据任务延迟最小的规则将任务迁移给所选择的节点.在此基础上，文献[23]提出了一种基于公平性调度度量的任务迁移算法，该算法考虑了任务迁移的能量消耗、雾节点的历史平均能量和雾节点的优先级三个重要特征，以提高雾节点能耗公平性并实现总能耗最小化.而在这些现有的方案之中，却仍然缺乏对雾节点距离、计算能力以及剩余能量等的联合考量，这可能会导致一些通信能耗的浪费或是雾节点的不合理分配.

基于上述挑战，本文提出了一种雾辅助物联网中公平节能的计算迁移方案，主要贡献总结如下：

● 通过对迁移决策以及雾节点分配给各个任务的计算和信道资源占比的联合优化，构建了一个最小化所有任务完成总能耗的优化问题.特别地，在迁移决策过程中融合考虑了公平性指标，该指标由雾节点的计算能力、剩余能量值、历史平均能耗值以及距离组成，通过考量该指标获得对雾节点能耗公平性最优的迁移决策.

● 基于上述混合整数非线性规划问题，提出基于动量梯度和坐标协同下降的公平性能耗最小化算法(Momentum gradient and coordinate collaboration descent based fair energy minimization,MGCCDFEM)，用于求解最小化能耗.该算法通过融合坐标下降法[24](Coordinate descent,CD)和动量梯度下降法[25](Momentum gradient descent，MGD)，获得雾节点分配给各个任务的计算和信道资源占比的最优值，从而实现总能耗最小化.

● 仿真结果进一步验证了上述算法的有效性，相比于传统梯度下降法，所提算法的收敛速度提升了35%.同时，相比于其他两种基准迁移方案，网络寿命分别平均提升了23.6%和31.2%.进一步地，该算法在不同雾节点数量以及不同任务大小的环境下仍然能够保持性能优势，体现了本文算法在环境免疫性上的优势.

本文其余部分组织如下：第一节介绍了本文的网络模型；第二节是对优化问题的描述；第三节是对本文所提出的MGCCD-FEM 算法的具体介绍；第四节是仿真结果与分析；最后，第五节总结全文.

1 网络模型

1.1 系统模型

本文构建了一个三层的物联网雾计算迁移模型，如图1 所示，分别包含云层、雾层和感知层，每层的具体功能定义如下.

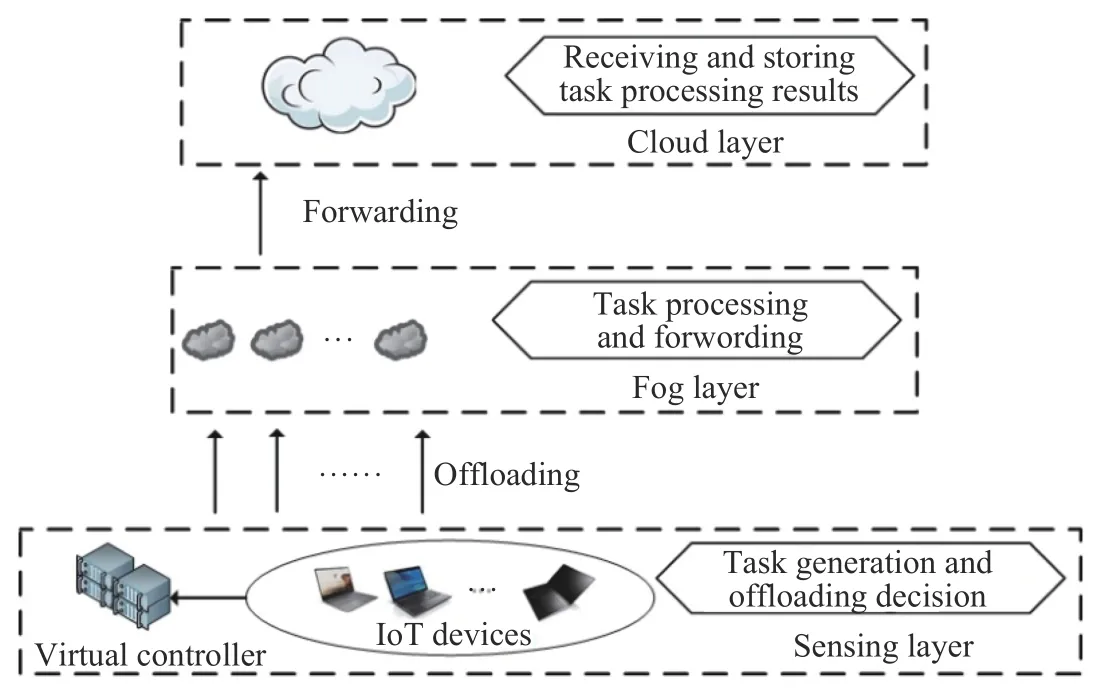
图1 网络模型Fig.1 Network model

感知层：感知层由m个物联网设备组成，部署在相应场所进行数据收集，该物联网设备（或由其生成的任务）表示为集合M.在每个时间段T内，各个物联网设备都会生成一个计算任务待处理.由于在每个时间段内，每个设备只会对应一个任务，因此本文将任务i（i∈M）表示物联网设备i生成的任务，且不同的物联网设备产生的任务大小不同.同时，感知层生成的全部任务都将迁移至雾节点进行处理.感知层存在一个虚拟控制器，其功能是每隔时间段T，按照任务生成顺序，选择对每个任务而言，公平性指标最高的雾节点进行迁移.

雾层：雾层作为感知层和云层的中间层，部署在网络边缘.该层包含n个用于处理任务的雾节点，雾节点表示为集合N，且都能够和感知层中的物联网设备进行交互.与物联网设备相比，雾节点具有更强的计算能力.基于感知层所做的迁移决策，分配计算与带宽资源，实现任务处理能耗的最小化，处理完毕后将处理结果反馈给感知层并转发给云层做备份存储.

云层：云层接收并存储雾层传输的任务处理结果，实现数据备份.

1.2 计算模型

本文定义任务i(i∈M)大小为Li(Mb)，Cj(Mb·s-1)表示雾节点j(j∈N)的计算能力，表示雾节点j的计算功率.

（1）任务处理总时延.

(a)传输时延

任务i传输到雾节点j的传输时延表示为：

其中，Rij表示任务i传输至雾节点j的传输速率，αij表示任务i的迁移决策值（根据公平性指标决定，若任务i决定迁移至雾节点j处理，则该值为1，否则为0），具体可以表示如下：

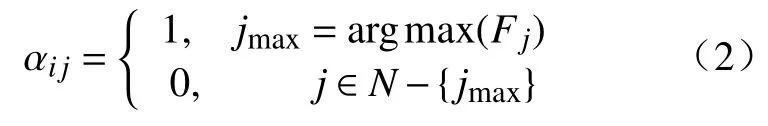
其中，Fj表示公平性指标，该指标旨在表明某个任务迁移至雾节点j时，雾节点能耗的公平性大小.本文将选择对于每个任务而言，雾节点能耗公平性指数最高的雾节点进行迁移.公平性指标Fj可以表示为：

传输速率Rij表示为：

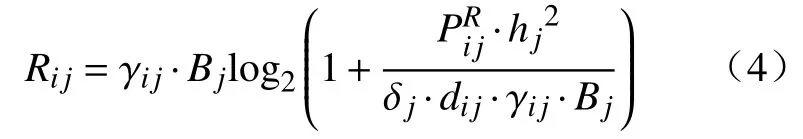
其中，γij表示分配给任务i的雾节点j带宽占比，Bj表示雾节点j的带宽，hj表示雾节点j的信道增益，δj表示雾节点j的信道噪声,表示任务i传输至雾节点j的传输功率.

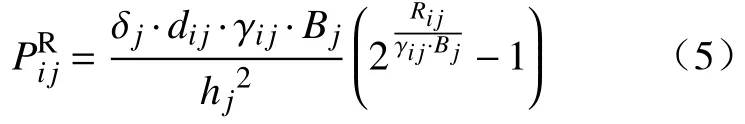
(b)计算时延

雾节点j计算任务i的计算时延表示为：

其中，βij表示雾节点j分配给任务i的计算能力占比.

则雾节点j处理任务i的总时延Tij可以表示为：

（2）任务处理总能耗.

(a)传输能耗

传输过程的总能耗ER可以表示为：

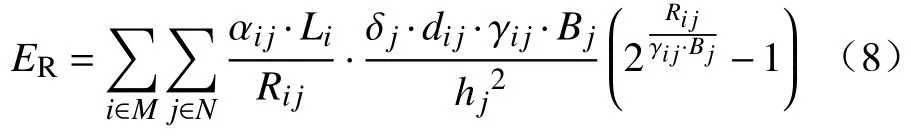
(b)计算能耗

任务计算过程的总能耗EC可以表示为：

2 雾辅助物联网中公平的任务处理总能耗最小化问题

本文的优化目标为通过联合优化任务i的迁移决策值 αij、雾节点j分配给任务i的计算能力占比 βij和带宽占比 γij，以最小化物联网中所有任务处理的总能耗.该优化问题P1 具体构建如下：

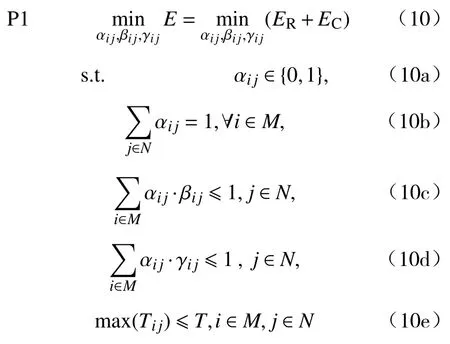
目标函数(10)即为最小化所有任务处理的总能耗E.约束(10a)表示迁移决策的取值为0 或1；约束(10b)表示设备i只会选择一个雾节点作为迁移目标；约束(10c)雾节点计算资源分配的约束，即分配给所有迁移到雾节点j的计算任务的总计算资源占比不能大于1；约束(10d)表示通信资源分配的约束，即分配给雾节点j的迁移任务的带宽总占比不能大于1；约束(10e)表示任务的最大处理时间不能大于最大容忍延迟T.

3 基于动量梯度与坐标协同下降的公平性能耗最小化算法

明显地，由于变量 αij的取值为离散的整数，而其他两个变量 βij和 γij为连续值，因此，上述优化问题是一个混合整数非线性规划问题.为了更好地求解优化问题P1，本文主要将求解过程分为以下两个部分：

(1)迁移决策求解.

由于变量 αij为离散的整数，使优化问题求解变得困难.因此，本文首先利用公式(2)确定迁移决策 αij的取值，获得最优迁移决策取值.于是，传输能耗可以进一步表示为：

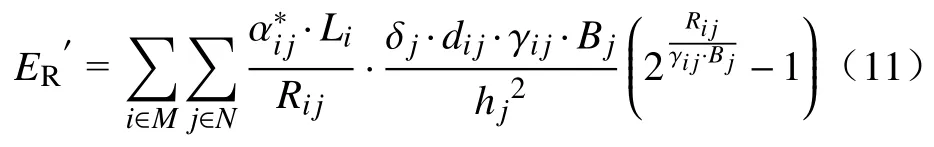
计算能耗可以表示为：

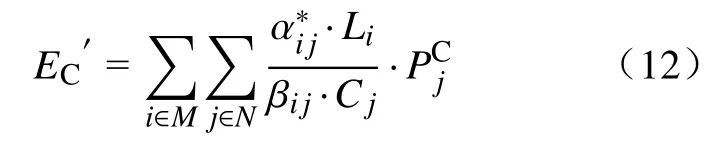
则优化问题P1 即可转换为优化问题P2，具体表示如下：

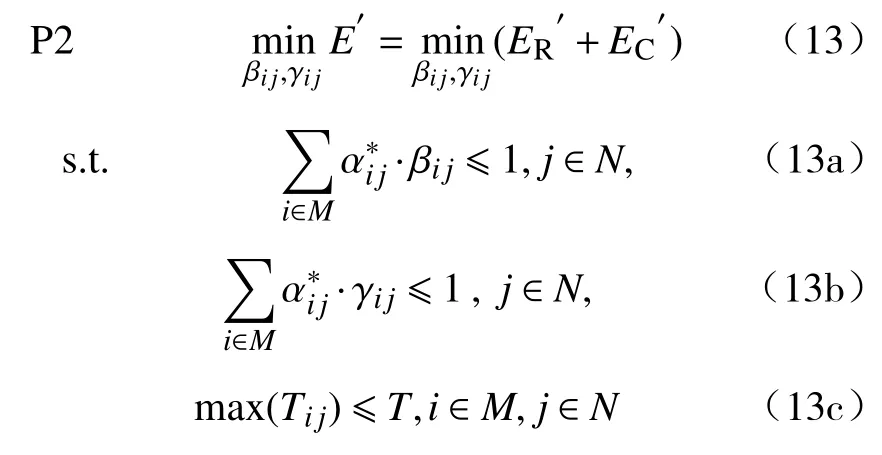
(2) 最优计算资源与带宽占比的求解.

为了更加快速和精确地求出P2 问题的最优解，融合动量梯度下降与坐标下降思想，提出了基于动量梯度与坐标协同下降的公平性能耗最小化算法（MGCCD-FEM），该算法求解过程大致如下：

首先，将优化问题P2 表示为f(βij,γij)，并选取雾节点的计算资源占比 βij以及带宽占比 γij的初值.

可证明优化问题P2 的Hessian 矩阵正定，进一步可以表明优化问题P2 是一个可微凸函数，优化问题P2 成为了一个凸优化问题.因此，问题P2 利用坐标下降法能够寻求到全局最优值.根据坐标下降法的原理，首先固定 γij，将 βij作为自变量.接着，采用协同的动量梯度下降法进行迭代得到本轮最优值，具体计算过程如下所示.

问题P2 关于 βij的偏导数可以表示为：

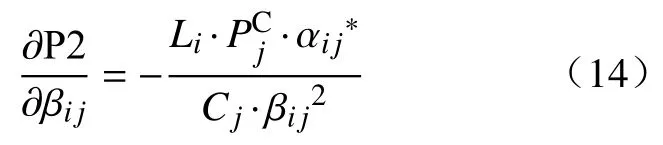
接下来，可以利用动量梯度下降法来更新变量 βij：

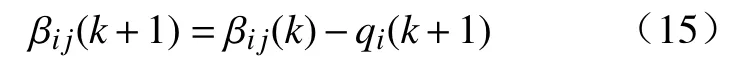
其中，累计动量qi(k+1)可以表示为：

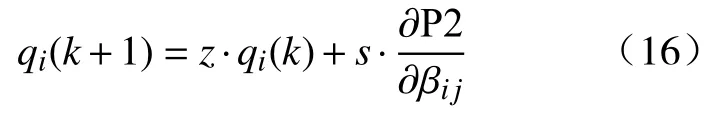
其中，k表示迭代次数，s表示迭代步长，z表示衰减值.

当达到停止条件，即达到最大迭代次数时，本轮迭代将停止，并得到本轮迭代中雾节点j分配给任务i的计算能力占比的最优值 βij*.

随后，同理可得，将得到的 βij*代入原函数，将γij作为自变量.同样的，通过数学证明，问题P2 关于 γij的二阶偏导数为正，因此问题P2 是关于 γij的可微凸函数.因此，也同样能够利用协同的动量梯度下降法进一步迭代得到本轮的最优值f(βij*,γij)，具体的计算过程如下所示.

问题P2 关于 γij的偏导数可以表示为：

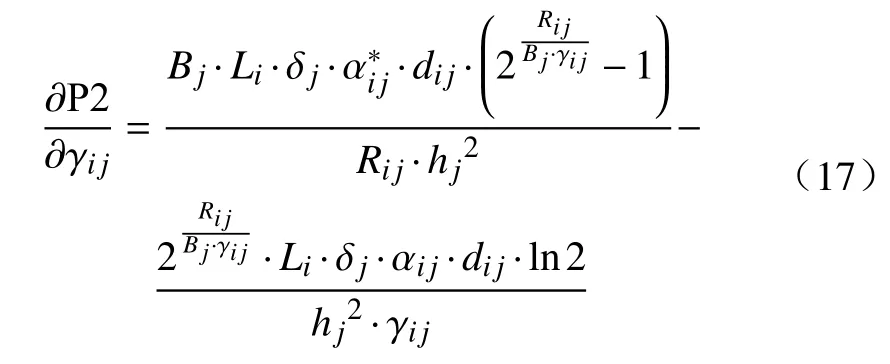
接下来，可以利用动量梯度下降法来更新变量 γij：

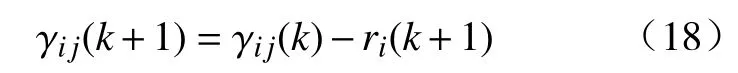
其中，累计动量ri(k)可以表示为：

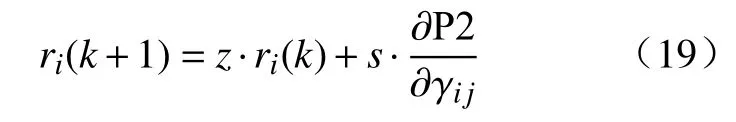
当达到停止条件，即达到最大迭代次数时，本轮迭代将停止，并得到本轮迭代中分配给任务i的雾节点j带宽占比的最优值 γij*.

在得到本轮迭代后的一组最优值 (βij*,γij*)之后，若满足全局迭代终止条件，则得到最终的雾节点j分配给任务i的计算能力占比及分配给任务i的雾节点j带宽占比的最优值 (βij**,γij**)，否则进入下一轮迭代.本文设定迭代终止条件为达到预定迭代次数k或是不满足约束条件(13a)，(13b)和(13c)中的某一个.

相对传统梯度下降法而言，MGCCD-FEM 算法在每步迭代中仅需求解一维搜索问题，所以对于某些复杂的问题计算更为简便.为更好地理解本文所提出的MGCCD-FEM 算法，算法1 将上述计算过程表示如下：

4 仿真与性能评估

本节通过仿真实验评估MGCCD-FEM 算法的有效性，并将本文所提方案与其他经典方案进行对比，以证明本文所提出的计算迁移方案的性能优势.

在本仿真环境中，假设存在10 个雾节点以及20 个本地物联网设备.核心的参数值设置如下：每个时间周期内的任务大小设置为10～50 之间的随机值；各个雾节点的计算能力分别设置为25,16,18,30,28,16,29,40,15,24 Mb·s-1;各个雾节点的计算功率设置为12,13,16,20,17,18,10,8,14,15W;所有物联网设备初始能量值设置为200 J,雾节点的满能量值设置为1500 J，各个雾节点的初始剩余能量占比设置为0.8,0.7,0.6,0.8,0.4,0.6,0.75,0.5,0.9,1;各个雾节点的历史平均能耗初值设置为85,60,90,100,78,75,50,110,99,87 J;各个雾节点的带宽设置为20,23,25,17,29,30,20,29,18,19 Mb·s-1；各个物联网设备的传输功率设置为2,1,1.3,1.4,1.8,1.6,2,2.2,1.1,1,1.8,1.9,2.1,2,2,1.4,1.7,0.5,2,1.6 W;每个时间周期设置为5 s.

图2 描绘的是在MGCCD-FEM 算法中的每一轮迭代中，采用传统梯度下降法和采用动量梯度下降法的不同情况下对总能耗的影响.从图中可以看出，在相同步长条件下，与传统梯度下降法相比较，动量梯度下降法的收敛至最优值的速度更快.同时，结果表明，步长越大，收敛速度越快.然而，为了获得更快的收敛速度而无休止地增加步长是不可取的.若步长超过一定限制，收敛值波动会变得极大，最终导致其无法收敛到最优值.仿真结果验证了动量梯度下降法的有效性以及与传统方法相比在收敛速度上的优势.

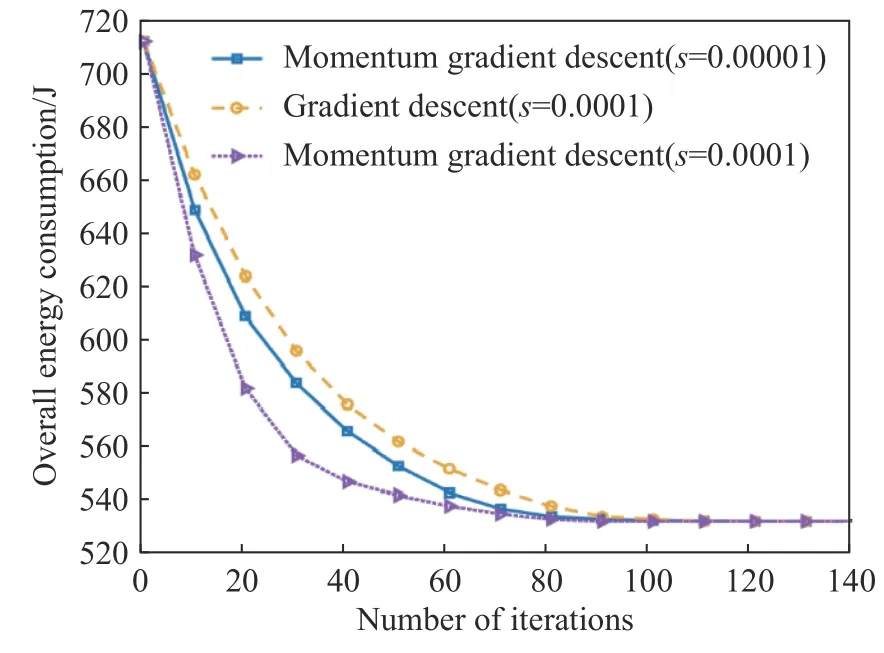
图2 动量梯度下降法和传统梯度下降法的总能耗对比Fig.2 Comparison of the total energy consumption between the momentum gradient descent and gradient descent

接下来的图3 至图5 所展示的仿真结果是通过将本文所提出的方案与其他两种相关方案进行对比，从而进一步突出本文方案的性能优势.“Proposed method”表示本文提出的方案；“Random selection scheme”表示雾节点随机选择迁移方案，该方案在进行迁移决策时，不设定迁移标准，在雾节点中随机选择；“Greedy task offloading (GTO)”方案代表文献[23]所提出的贪婪任务迁移方案，该方案倾向于选择迁移过程中计算能耗最低的雾节点.

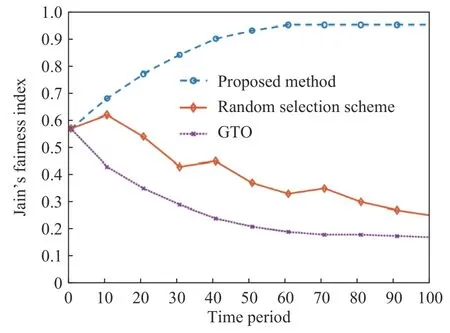
图3 Jain’s 公平指数三种方案对比Fig.3 Comparison of the Jain’s fairness index for the three different schemes

图3 描述了三种方案随着时间周期的迭代，Jain’s 公平指数的不同变化情况，Jain’s 公平性指数f表示如下：

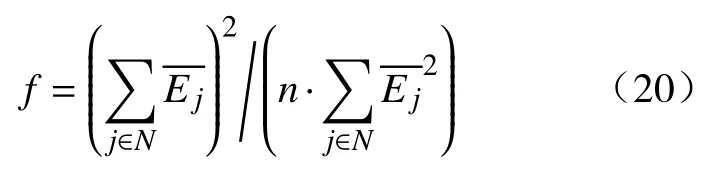
该指标用来评价本文所提出的迁移机制在能耗均衡性方面的优劣，从图中可以看出，本文提出的迁移方案的Jain’s 公平指数随时间不断增高，这是由于该迁移方案按照雾节点能耗公平性指标进行迁移决策，提高了雾节点能耗的公平性.同时，很明显能够看出本文方案的Jain’s 公平性指数要远远高于其他两种方案，这是由于另外两种方案的迁移决策分别聚焦于随机选择和能耗最小化，而忽略了雾节点能耗的公平性.最后，本文定义网络寿命为雾节点能量全部耗尽或物联网设备能量全部耗尽的时间，本文方案相较于其他两种方案，网络寿命分别平均提升了23.6%和31.2%，验证了该方案最大化网络寿命的有效性.

图4 展示了三种方案随着时间周期的迭代，总能耗的不同变化情况.显然地，由于每个时间周期内都会产生相应能耗，因此，三种方案的总能耗曲线都呈上升趋势.此外，从图中可以看出，最初总能耗最低的是GTO 方案，这是由于该方案倾向于迁移到计算能耗最低的雾节点，而在持续迁移过程中，通信能耗不断增长，最终难以抵消降低的计算能耗，因此后续总能耗的数值较本文迁移方案更高一些.而本文的迁移方案由于考虑了雾节点与本地物联网设备的距离因素，偏向于选择距离更近的雾节点，因此其通信能耗会较其他两个方案有所降低，后续的总能耗表现最优.

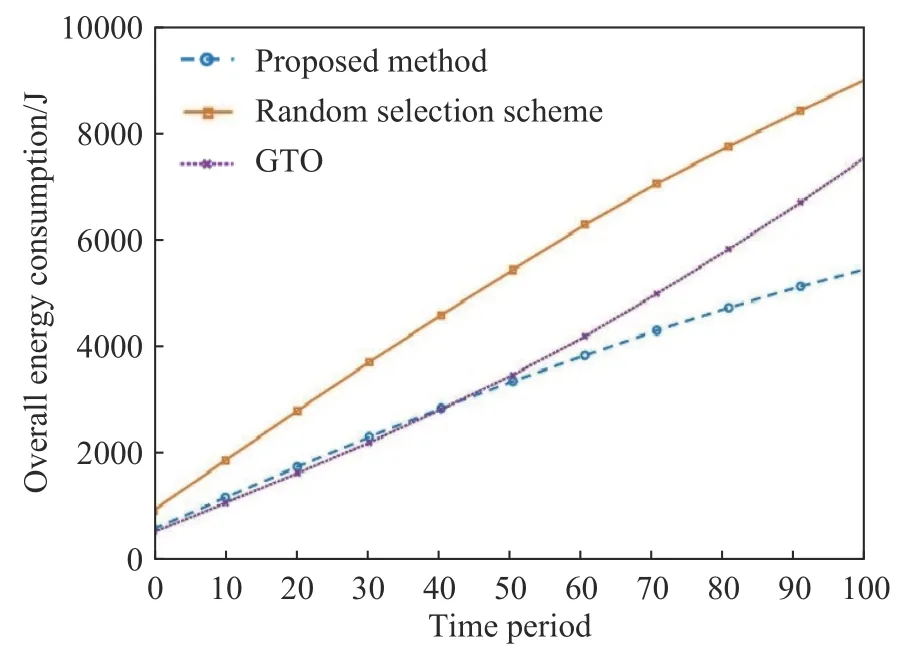
图4 总能耗的三种方案对比Fig.4 Comparison of the total energy consumption for the three different schemes

图5 分析了三种方案随着时间周期的迭代，雾节点总历史平均能耗的不同变化情况.同样的，由于每个时间周期内都有相应数量的雾节点产生计算能耗，因此三种方案的曲线都呈现上升趋势.其中，GTO 方案的雾节点总历史平均能耗最低，本文方案其次，随机选择方案最高.这是由于GTO 方案始终以最小计算能耗雾节点作为迁移对象，因此其雾节点的历史平均计算能耗也最低，但其在总能耗和雾节点能耗公平性方面表现远远不如本文所提出的方案.

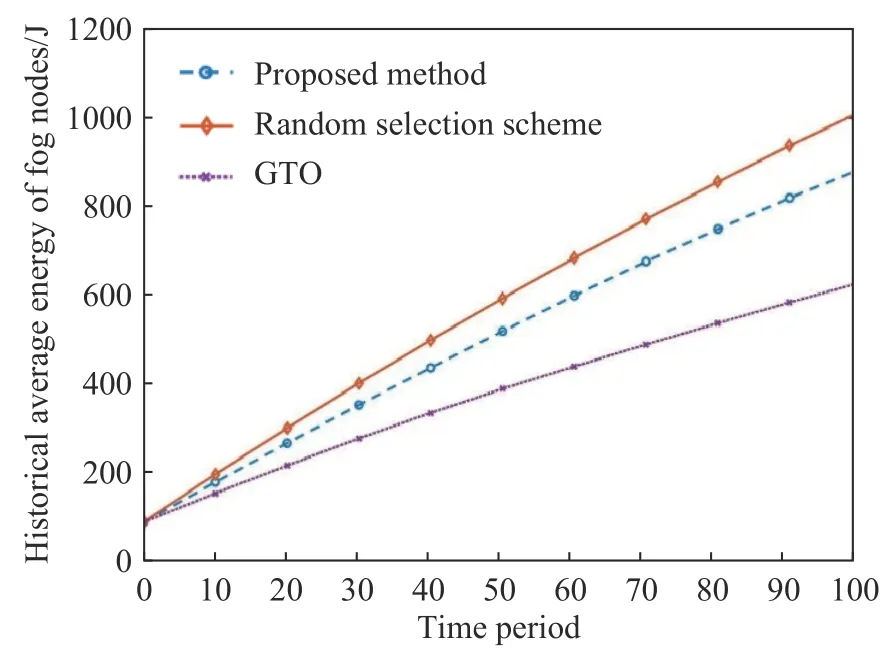
图5 雾节点总历史平均能耗的三种方案对比Fig.5 Comparison of the total historical average energy consumption for the three different schemes

图6 展示随雾节点和本地物联网设备的平均距离的增加，在不同平均任务大小的情况下，总能耗的变化情况.从图中可以看出，在平均距离一定的条件下，平均任务大小越大，总能耗越高.明显地，若平均任务大小越大，处理这些任务的计算能耗和传输能耗越大，总能耗也会随之增加.同时，在平均任务大小一定时，平均距离越大，总能耗越高.这是由于若平均距离越大，说明雾节点和本地的物联网设备距离越远，传输任务所需要花费的传输能耗越大，导致总能耗增加.

图6 总能耗关于平均距离以及平均任务大小的对比Fig.6 Comparison of the total energy consumption versus the average distance and average task size

图7 表明了随雾节点和本地物联网设备的平均距离的增加，在不同雾节点数量的情况下，Jain’s公平性指数的变化情况.由图可知，在雾节点数量一定的情况下，若平均距离越大，Jain’s 公平性指数越低.这是由于随着平均距离增大，距离较远的雾节点被选择的几率不断下降，导致雾节点的能耗公平性不断降低.而同时，在平均距离一定的情况下，随着雾节点数量的增多，Jain’s 公平性指数也会降低.这是因为雾节点数量增多时，具有高处理能力的空闲雾节点出现的概率就会增大，未被选择的雾节点数量也会增多，导致雾节点能耗的公平性不断降低.

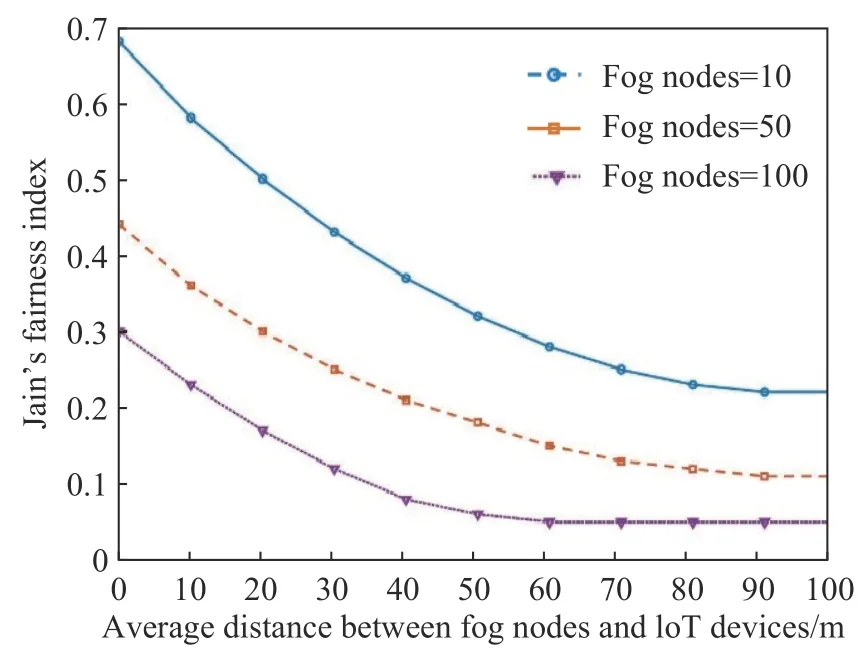
图7 Jain’s 公平指数关于平均距离以及雾节点个数的对比Fig.7 Comparison of the Jain’s fairness index versus the average distance and number of fog nodes

5 结论

为了进一步提高物联网的生命周期并降低任务处理过程的总能耗，本文提出了一种雾辅助物联网中公平节能的计算迁移方案.通过对迁移决策、雾节点分配给各个任务的计算和信道资源占比的联合优化，构建了一个最小化所有任务完成总能耗的优化问题.基于上述混合整数非线性问题，提出了MGCCD-FEM 算法.首先，根据能耗公平性指标来计算能耗公平性最优的迁移决策；随后，通过所提出的基于动量梯度和坐标的协同下降法，得到最优的计算和信道资源占比，达到最小化总能耗的目的.最后，经过大量仿真与分析，与其他几种迁移方案相比，本文方案能够获得最低的总能耗以及最高的公平性，并且该方案在不同环境下都能够保持自身稳定的性能优势.