RDX分子内振动能量重分配的动力学研究

张伶育，张继龙，曲泽星

（吉林大学化学学院,理论化学研究所,长春 130023）

环硝胺六氢-1，3，5-三硝基-1，3，5-三嗪（RDX）在分解过程中可释放大量的能量，是推进剂和炸药的主要成分［1～3］.RDX在外界能量加载下，最终分解并释放能量的过程可分为以下4个阶段：（1）声子激发过程，在外界能量加载过程中（如冲击波），首先产生机械波，这些机械波将激发晶格间的声子［4～7］；（2）分子间到分子内振动能量传递过程（Vibrational Energy Transfer，VET），晶格间振动产生的声子可通过多声子的“上泵”（Up-pumping）过程，将能量传递到分子内的振动模式上（Doorway模式）［8～11］；（3）分子内振动能量重分配过程（Intramolecular Vibrational Energy Redistribution，IVR），当多声子的“上泵”能量高于分子内振动模式的基态振动能级时，这些振动模式会被激发到更高的振动能级上（即发生振动激发），同时，这些被激发的振动模式还可通过与其它振动模式之间的耦合进行能量传递，并将多余能量重新分配，其中包括将能量传递到那些可促进RDX分解所需的N—N键的振动模式上［12～15］；（4）RDX分解放热过程，当能量持续汇集到N—N键的振动上时，其振动能量提高到超出N—N键解离能的水平，导致N—N键的断裂，继而引发后续的分解反应并释放大量的热量.在上述的4个阶段中，RDX分子内振动态被激发并将能量重新分配、转移到N—N键的振动模式上是其分解反应的关键，对其振动耦合能量转移过程的研究，有助于更加深入地理解RDX的分解及能量释放机制.

通常，最低频率的分子内振动模式具有最快的激波诱导转变速率，同时这些低频的分子内振动模式（通常为弯曲振动）的振动频率跟晶格间的声子振动频率最为接近，因此多声子的“上泵”激发应该首先激发这些低频的分子内振动模式.Yang等［16］利用宽带“fs-CARS”光谱技术，通过同时集体激发RDX分子晶体的多个振动模式，并观测各振动模的耦合动力学过程，发现振动频率约为466和672 cm-1两个振动模式是声子进入分子的两个重要的Doorway振动模式.最近，Kumar等［17］基于“三声子”（3-Phonon）模型，计算并统计了RDX分子内所有振动模式间的“模间散射率”及“带间散射率”.通过计算发现，分子内的低频振动模式之间存在较强的耦合，其模式之间的能量传递十分迅速，而这些低频振动模式与N—N伸缩振动模式之间的耦合较小.因此，通过低频振动模式的激发，仅会将极少的能量直接传递到N—N伸缩振动模式上.然而，中频振动模式，特别是457～462 cm-1及831～1331 cm-1的中频振动模式，则与N—N伸缩振动模式耦合较大，是将能量汇集到N—N键上并引发N—N键解离的关键振动模式.除了振动模式耦合的影响，外界加载能量的不同也会对分子内的振动能量转移过程产生较大的影响.Zerilli等［18］基于理论模拟，通过对硝基甲烷固体中激波诱导的内模态之间的非辐射跃迁率的研究发现，硝基甲烷在50～300×108Pa的冲击下，其跃迁速率比正常情况下提高了6～10个数量级，这意味着不同的加载能量会显著影响分子内模间跃迁速率.

分子内不同振动模式间的耦合来源于其振动的非谐性［19］，基于传统分子力场的动力学模拟无法描述分子振动模式间的耦合，因此必须基于量子力学水平下的分子动力学模拟才能充分考虑其非谐效应［20］.本文以RDX单分子为模型，通过从头算分子动力学模拟（BOMD），构建其分子内振动模式间耦合矩阵，基于该耦合矩阵，搜寻能量从低频振动模式到高频振动模式的最优传输路径，揭示能量在RDX单分子内传递的微观机制.

1 计算方法

1.1 构型优化及频率分析

首先，在B3LYP/6-31+G（d）［21］和PM6［22］基础上分别优化了单分子RDX的几何构型，并计算了相应的振动频率.经比较发现，对于单分子RDX基态构型的优化及频率计算，半经验的PM6方法可以较好地重现DFT方法的计算结果（详细数据见表S1～表S3，本文支持信息）.考虑到计算成本，后续基于Born-Oppenheimer近似的分子动力学模拟（BOMD）［23，24］，将在PM6水平下进行.

1.2 从头算动力学模拟

在BOMD计算中，对RDX单分子中的57个简正振动模（Normal mode）分别进行激发（加载能量），之后在微正则系综（NVE）下，基于不同的加载能量进行BOMD模拟，从而获得一系列的动力学轨迹.

1.3 构建“模-模耦合图”

为了获得RDX单分子中不同振动模式之间的耦合，用下式将某一加载条件下BOMD得到的动力学运动轨迹与RDX的所有简正振动模作内积（投影）［25］.

式中：Cij为第i和j两个振动模式之间的能量转移概率；v⇀j为第j个简正振动模；V⇀it为当能量加载到第i个振动模式时，BOMD在t时间处的归一化速度；N为BOMD模拟步数.通过式（1）即可获得给定的第i个振动模式分布到其余振动模式上的概率，即能量转移概率.基于式（1）对所有加载能量进行操作，并统计平均即可获得在不同加载能量下所有振动模式之间的能量转移概率.为了方便表达，借助下式获得不同振动模式间的耦合强度因子（dij）：

通过式（2）获得所有振动模式间的耦合强度因子，可构建57×57的“模-模耦合矩阵”，由此可绘制出“模-模耦合图”.

1.4 最优路径的搜寻

基于上述得到的“模-模耦合图”，可以获得任意两个振动模式之间能量传递的最优路径.在搜寻过程中，从初始模式出发，对于每一步均选取与该振动模式具有最大耦合（耦合强度因子最小）的振动模式作为能量传输的下一振动模式.为了避免出现传输路径循环的问题，在每一步传输过程中需避免已经在前序过程涉猎的振动模式，依此类推达到目标振动模式，即可获得最优的能量传输路径.

上述所有几何构型优化、频率分析及BOMD模拟都是借助Gaussian 16软件［26］完成的.动力学轨迹分析，“模-模耦合图”的构建以及最优能量传输路径的搜寻都基于我们自编的脚本实现的.

2 结果与讨论

2.1 振动模式分析

基于优化后的RDX单分子构型，首先对其振动模式进行分析.如表1所示，将RDX单分子的57个简正振动模（N.M.）按照频谱划分为低频（Low frequency，LF）、中频（Medium frequency，MF）、高频（High frequency，HF）和超高频（Ultra-high frequency，UHF）4个频段.其中，低频包含6个简正振动模（1～6），对应频率范围为46.88～91.36 cm-1，其主要振动方式为—NNO2基团的旋转运动（见图S1和图S2，本文支持信息）.中频包含15个简正振动模（7～21），对应频率范围为204.40～696.69 cm-1，其主要振动方式为—NNO2基团和—CH2—基团的摇摆运动（见图S2～图S6，本文支持信息）.高频（22～51）可以分为5组：第一组包含6个简正振动模（22～27），对应频率范围为711.72～924.00 cm-1，其主要振动方式为—NNO2基团的弯曲运动（见图S6和图S7，本文支持信息）；第二组包含12个简正振动模（28～39），对应频率范围为956.59～1265.75 cm-1，其振动方式为—CH2—基团的旋转、剪刀、弯曲和摇摆的混合运动（见图S7～图S10，本文支持信息）；第三组包含3个简正振动模（40～42），对应频率范围为1299.18～1309.35 cm-1，其主要振动方式为—NNO2基团的伸缩运动和—CH2—基团的旋转运动的混合运动（见图S10和图S11，本文支持信息）；第四组包含3个简正振动模（43～45），对应频率范围为1327.85～1342.02 cm-1，其主要振动方式为—CH2—基团的弯曲运动（见图S11和图S12，本文支持信息）；第五组包含6个简正振动模（46～51），对应频率范围为1393.09～1787.83 cm-1，其主要振动方式为—NNO2基团的对称与反对称伸缩运动.其中，3个简正振动模（46～48）中两个N—O键沿着键轴方向同时伸长或缩短，为对称伸缩振动模式（见图S12）；3个简正振动模（49～51）中一个N—O键沿着键轴方向伸长的同时，另一个N—O键沿着键轴方向缩短，为反对称伸缩振动模式（见图S13，本文支持信息）.超高频包含6个简正振动模（52～57），对应频率范围为2586.50～2672.16 cm-1，其主要振动方式为—CH2—基团的不对称伸缩运动（见图S13～图S15，本文支持信息）.

Table 1 Contribution of various groups to the normal mode(N.M.)of RDX

2.2 “模-模耦合图”

计算了不同加载能量下的振动模式耦合图（见图S16～图S24，本文支持信息），通过比较低加载能量下的振动模式耦合图发现，当加载能量低于165.31 kJ/mol时，振动模式v3展示出正常的耦合方式；当加载能量高于165.31 kJ/mol时，振动模式v3展示出反常的耦合方式，因此，分别在加载能量低于和高于165.31 kJ/mol处各选取了一个典型的加载能量的耦合图作为讨论对象（图1）.值得注意的是，模拟中加载的能量是体系的总动能，伴随动力学模拟，能量会弛豫到所有振动模式上直至达到平衡.在加载能量分别为141.69 kJ/mol［图1（A）］和212.57 kJ/mol［图1（B）］时，基于RDX单分子BOMD模拟轨迹，利用式（1）和式（2）得到的不同加载能量下的“模-模耦合图”.图中颜色越趋于红色表明dij越大，振动模式之间的Cij越小；反之颜色越趋于蓝色则dij越小，振动模式之间的能Cij越大.由于处在红色区域的振动模式向其余的振动模式进行能量转移的概率很小，所以能量在这些振动模式上很容易局域化，换言之，处于红色区域的振动模式可以很好地积聚能量从而引发后续的化学反应.

Fig.1 Mode-mode interaction matrix for initiation energy of 141.69 kJ/mol(A)and 212.57 kJ/mol(B)

通过分析两种不同加载能量下的“模-模耦合图”，发现处于红色区域的振动模式主要可分为I（v20～v30），II（v33～v38），III（v40～v42）和IV（v46～v51）4组，其中第I，III和IV组中的振动模式主要集中在—NNO2基团上，第II组的振动模式主要集中在—CH2—基团上（表1），说明—NNO2基团更容易局域化能量（有利于能量累积），从而进一步引发N—N键的断裂.此外，通过对比不同加载能量下的“模-模耦合图”可见，在高加载能量下，红色区域的面积在缩小，这是因为加载能量越高，各振动模式对应的振动能级将越高，其非谐性增大，导致其与其余振动模式之间的耦合也将越大，能量更易流出（转移），dij更小，图中颜色越趋于蓝色.但有趣的是，在高加载能量下振动模式v3附近的颜色更趋于红色，表明在高加载能量下其能量转移概率反而减小.

2.3 最优能量传输路径

基于图1，可以获得任意两个振动模式之间的最优能量传输路径.通常，RDX分子中的低频（LF）振动模式的能量与声子更为接近，多声子的“上泵”能量转移更易传递到低频振动模式上，因此，着重考虑从低频振动模式出发的最优能量传输路径.表2收集了从v1～v66个低频振动模式出发，在加载能量分别为141.69和212.57 kJ/mol时，能量传输到振动模式v48的最优路径，并且在箭头上方标记出振动模式之间的能量传输概率（其余加载能量下的能量最优传输路径见表S4～表S10，对应的耦合大小见表S11～表S17，本文支持信息）.此处，高频振动模式v48是典型的N—N伸缩振动，所以这一过程相当于模拟能量如何从低频振动模式传递到N—N伸缩振动模式上.从表2可见，对于两种能量加载情况，最优传输路径均与振动模式v3和v4有关.因此，这两个振动模式在RDX分子内振动能量传递过程中起着至关重要的作用.同时，还发现振动模式v3与v48的能量传输概率最大，如果能量通过振动模式v3进行传输，则可直接传递到N—N伸缩振动模式上继而引发后续的化学断键反应.而如果能量传输通过振动模式v4进行，则需要经过中频振动模式v15，才能将能量进一步传递到高频振动模式最终到达N—N伸缩振动模式v48.

表2中用括号标记了与v48耦合最大的振动模式v24.振动模式v24与v48之间存在很大的能量转移概率，表明二者之间很容易实现能量的双向传递.从图1中可知，处于红色区域的振动模式v24很容易局域化能量，所以振动模式v24可被看作是一个“能量聚集器”，其在RDX单分子N—N键的断裂解离过程中扮演十分重要的角色.

Table 2 Optimal energy transfer pathway from low frequency normal modes(N.M.)to normal mode v48

2.4 振动模式v3和v4的比较

由上述研究发现，振动模式v3和v4在从低频振动模式到高频振动模式的能量传输过程中起着十分重要的作用，特别是振动模式v3在高加载能量下其耦合强度表现出截然相反的趋势（图1）.为了探究此现象的本质，分别计算了v3和v4两个振动模式沿着各自的振动方向扫描获得的势能曲线以及用二次函数拟合的势能曲线.如图2所示，振动模式v3表现为—NNO2基团的旋转运动，振动模式v4表现为—NNO2基团的弯曲运动.对于振动模式v4，其振动势能曲线可借助一个二次函数很好地拟合，且其势阱很浅（约20.91 kJ/mol）［图2（B）］，表明振动模式v4的势能面很平缓，具有很强的非谐效应，较易发生能量转移；而对于振动模式v3，单一二次函数很难拟合其势能曲线，但借助一个在平衡位置附近以及一个远离平衡位置的两个二次函数则可以很好拟合其势能曲线.振动模式v3在平衡位置附近，表现出与振动模式v4类似的平缓势能面（势阱约20.91 kJ/mol）；而在远离平衡位置时，表现出一个深势阱的振动模式图2（A），因此v3是一个包含两种振动方式的“双谐振耦合模式”.在低加载能量下，振动模式v3与其它振动模式耦合很大，容易发生能量转移；而伴随着加载能量的升高，振动模式v3则转变为一个深势阱的振动模式，反而有利于能量局域化，导致其在图1（B）中“变红”.

通过振动模式的分析，也可以进一步理解振动模式v3的“双谐振耦合模式”的本质.振动模式v3主要是—NNO2基团的旋转运动，当—NNO2基团旋转时，由于N—N键具有单键性质，所以其旋转较容易，对应其势能面也表现平缓.另一方面，由于—NNO2基团是一个具有四中心六电子的共轭Π键，其N—N键并不是一个真正的单键，只是当—NNO2基团旋转角度比较小时，由于共轭效应较弱，可近似看作是N—N单键的旋转；但当—NNO2基团旋转角度很大时，就会破坏整个体系的共轭效应，从而导致能量的急剧上升，使得—NNO2基团旋转不再容易，表现出较深的势阱.值得注意的是，从前面的讨论发现，低频振动模式v3与高频振动模式v48具有很强的耦合，可以直接发生能量转移.振动模式v48主要表现为—NNO2基团上N—N键的伸缩运动，而振动模式v3对应—NNO2基团上围绕N—N键的旋转运动，当围绕N—N键的旋转角度较大时，此时旋转破坏Π键所需的能量远比拉伸所需的能量大，则会发生从旋转到伸缩的转变，导致能量从振动模式v3直接转移到振动模式v48.由于在高加载能量下v3还更易发生能量局域化，因此在高加载能量下，v3→v48的能量传输路径，是一种十分重要且有效的能量传输方式.

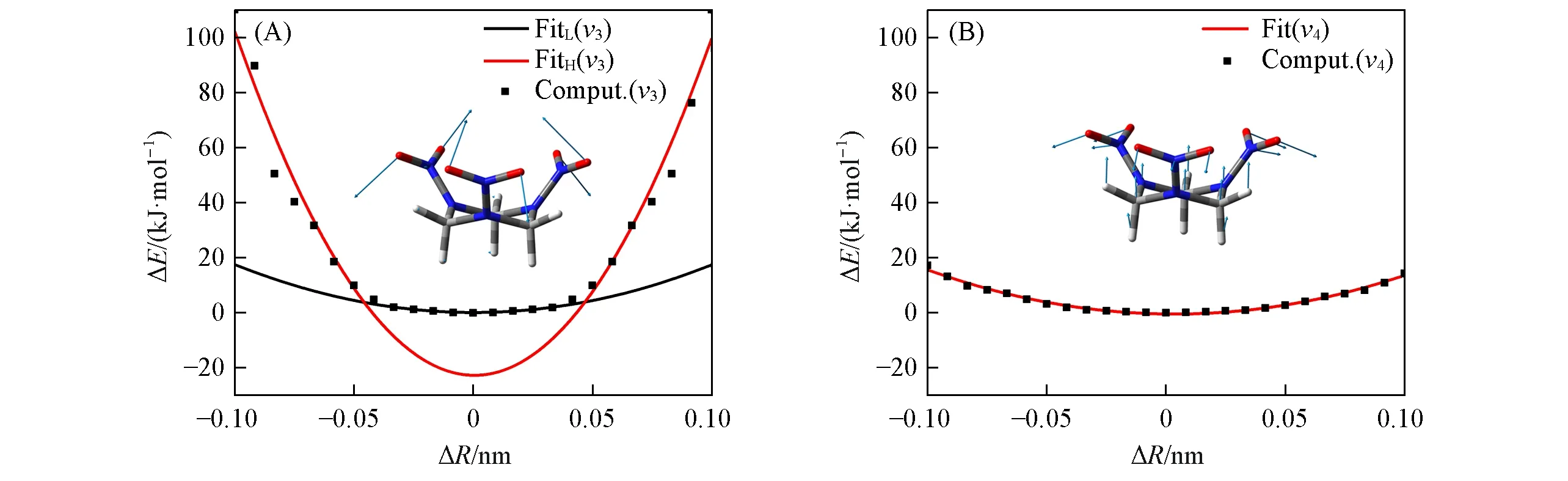
Fig.2 Potential energy curves computed with PM6 along normal mode v3(A)and v4(B)

3 结 论

借助从头算分子动力学模拟获得了RDX单分子振动耦合矩阵（“模-模耦合图”），基于该矩阵进一步找到了RDX单分子在不同加载能量下从低频振动模式到高频振动模式（主要是N—N伸缩振动）的最优能量传输路径.结果表明，RDX单分子中—NNO2基团往往表现出较弱的模间耦合，因此更有利于能量局域化.研究发现，在从低频振动模式到高频振动模式的能量传输过程中，振动模式v3和v4扮演十分重要的角色，它们在“机械能”到“化学能”的转换过程中起着“承上启下”的作用.通过对v3和v4两个振动模式的进一步分析，发现加载能量的不同，会导致RDX单分子能量传输路径的不同.当加载能量较低时，RDX单分子倾向于从低频振动模式到中频振动模式再到高频振动模式的能量传输路径；当加载能量较高时，低频振动模式v3则扮演十分重要的角色，从而导致能量从低频振动模式直接传输到高频振动模式上.本文研究揭示了RDX分子内振动耦合能量转移的微观机制，为进一步探索RDX将“机械能”转化为“化学能”的微观过程提供了理论基础.

支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20220393.