电主轴最佳跨距理论计算与仿真分析

刘永连,耿继青,何圳涛

(1.广东省高性能伺服系统企业重点实验室,广东珠海 519000;2.珠海格力电器股份有限公司，广东珠海 519000)

0 前言

主轴的跨距设计对主轴的力学性能有较大影响。目前，已有学者对主轴跨距的优化设计进行了相关研究[1-4]，但是大多数研究成果仅限于理论公式计算或仿真分析，未能对两者进行综合分析及评价，以提供有效的建议及方案，而且研究对象通常是结构十分简单的阶梯状光轴，与实际复杂的电主轴转动组件结构差异较大。陈维范和薛丹[1]对最佳跨距经验公式进行了详细推导，并利用有限元方法对车床机械主轴进行了静力学及模态分析仿真，但仅针对经验公式的计算结果进行了验证与对比，并未进行不同跨距的仿真分析，也未对固有频率及静刚度2种评价指标进行评估。李英明等[2]针对高速电主轴的光轴轴芯进行了以静刚度为优化目标的理论计算，同时建立以固有频率为优化目标的仿真计算方法，但未对这2种优化目标的合理性进行综合评估。刘军和周留洋[3]针对铣削加工中心电主轴进行了以静刚度及固有频率为优化目标的仿真计算，同样未对这2种优化目标的合理性进行评估。王晓明[4]针对阶梯状光轴进行了主轴静刚度实验验证与仿真，误差在3.11%以内，所研究的轴芯为实心光轴，与实际电主轴转动组件结构存在一定差异，并且未对优化目标的合理性进行评估。

本文作者基于现有研究成果，分析主轴变形形式，初步判断不同类型主轴可能的变形形式。针对某型电主轴，结合现有最佳跨距迭代经验公式进行理论计算；以径向1阶固有频率及径向静刚度为评价指标，建立仿真模型，计算不同跨距下评价的指标；总结各评价指标对跨距的影响规律，结合仿真结果及理论最佳跨距计算值，综合评价以径向1阶固有频率及径向静刚度为评价指标的合理性；提出电主轴跨距设计的一般原则，为主轴结构设计提供参考。

1 电主轴主要变形形式及最佳跨距理论计算公式

1.1 主轴主要变形形式分析

文献[2]中给出了电主轴的一般变形形式，但是不同类型电主轴的变形形式存在一定差异。车床电主轴轴芯直径较大且为空心结构，其轴芯弯曲刚度较高；高速电主轴轴芯直径较小，弯曲刚度远低于车床电主轴。根据材料力学理论[5]，电主轴模型可简化为简支梁结构，主轴静刚度主要由前轴承刚度、后轴承刚度及轴芯结构的弯曲刚度组成。当三者存在差异时，会表现为如图1所示的4种不同变形形式。

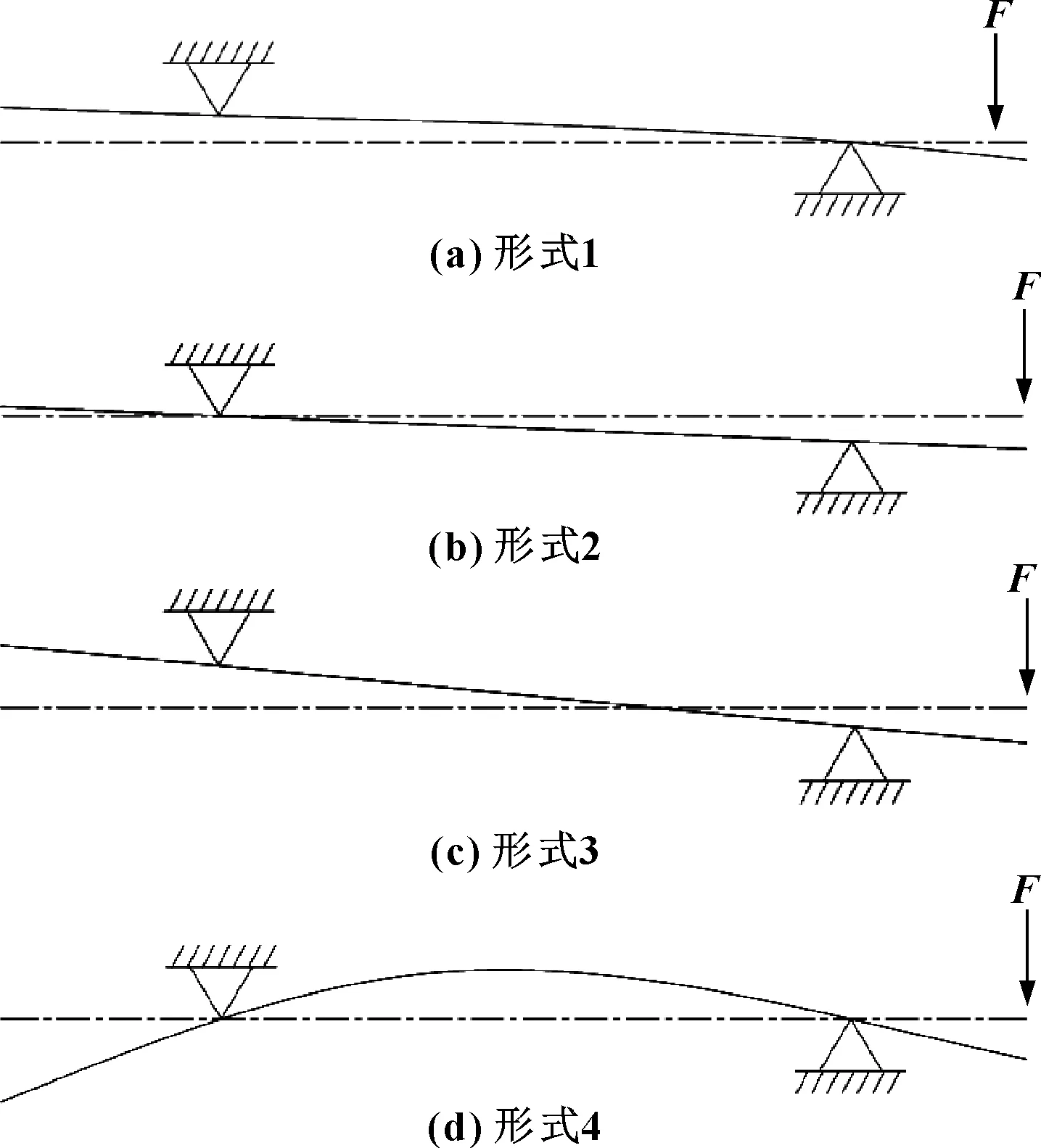
图1 主轴主要变形形式

当轴芯弯曲刚度相对前/后轴承偏高、后轴承刚度偏弱时，可能出现绕前轴承前俯后仰形式(变形形式1)。当轴芯弯曲刚度相对前/后轴承偏高、后轴承刚度偏大时，出现绕后轴承前俯后仰形式(变形形式2)。当轴芯弯曲刚度相对前/后轴承偏高、前/后轴承受力与变形量相当时，出现绕主轴中间某位置前俯后仰形式(变形形式3)。当轴芯弯曲刚度相对前/后轴承较弱时，出现主轴中间部分向上弯曲、轴头与轴尾向下弯曲的变形形式(变形形式4)。

一般情况下，车床电主轴倾向于变形形式1与形式3，而高速电主轴倾向于变形形式4，变形形式2出现的情况较少。不同变形形式的跨距变化对径向1阶固有频率及径向静刚度的影响可能会有一定差异。本文作者重点研究车床电主轴不同跨距下的径向1阶固有频率及径向静刚度的变化规律。

1.2 最佳跨距理论计算公式

参考文献[1-4]中的理论计算公式，利用Excel软件编制迭代算式，计算某型电主轴最佳跨距，结果如表1所示。

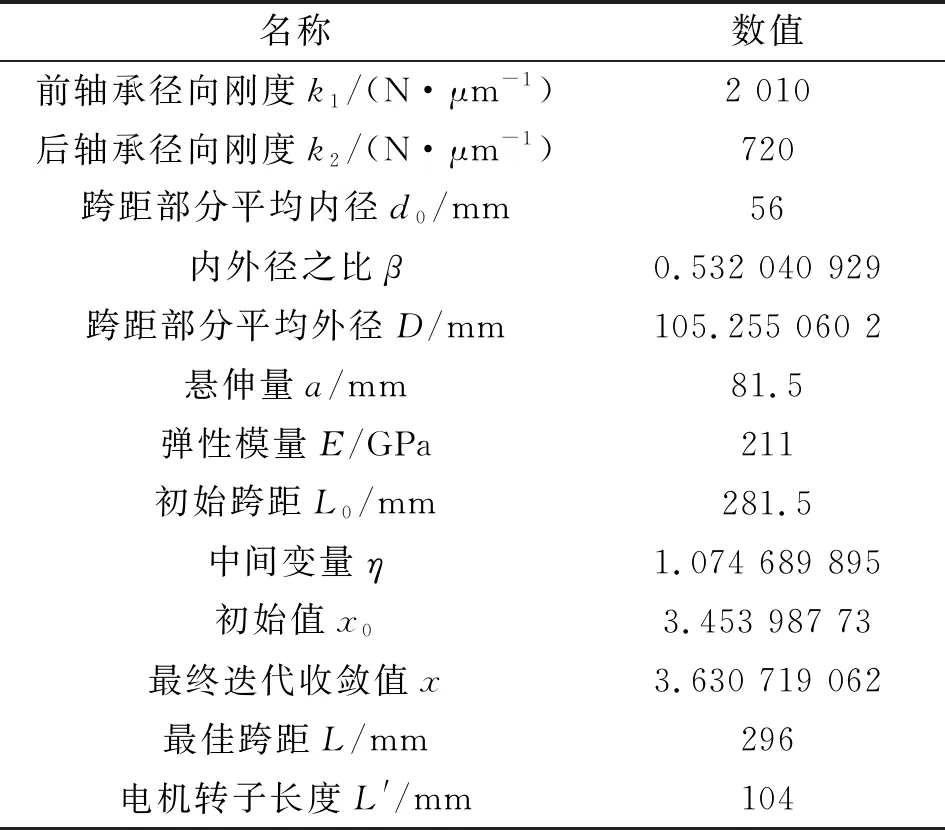
表1 某型电主轴最佳跨距理论计算结果

迭代以单位载荷下挠度最小为目标，公式为

y/F=a3/(3EI)·(L/a+1)+1/k1·[(a/L)2·

(1+k1/k2)+2a/L+1]

其中：y为主轴鼻端挠度，mm；F为主轴鼻端载荷，N；I为跨距部分截面平均惯性矩，mm4。

对上式中的跨距L进行求导，并令导数d(y/F)/dL=0， 得到：

(L/a)3-6η(L/a)-6η(1+k1/k2)=0

其中：

η=EI/(k1a3)

令x=L/a，利用牛顿迭代法，可得迭代算式：

(3xi2-6η)i=0,1,2,…

通过迭代计算可知，某型电主轴初始跨距为281.5 mm，而迭代后最佳跨距为296 mm。

2 电主轴跨距设计仿真模型验证

基于文献[1-4]中的仿真建模方法，以某型电主轴为例，取转动部分为对象进行仿真建模，如图2所示。电机转子及其他零部件或以锁紧螺母方式紧固在轴芯上，或以键连接方式固定在轴芯上。前轴承与后轴承内圈分别与主轴转动部分连接；外圈与轴承座连接，为非转动件。轴承起支撑转轴的作用，具有一定的刚度属性，在仿真模型中施加轴承模块进行仿真。

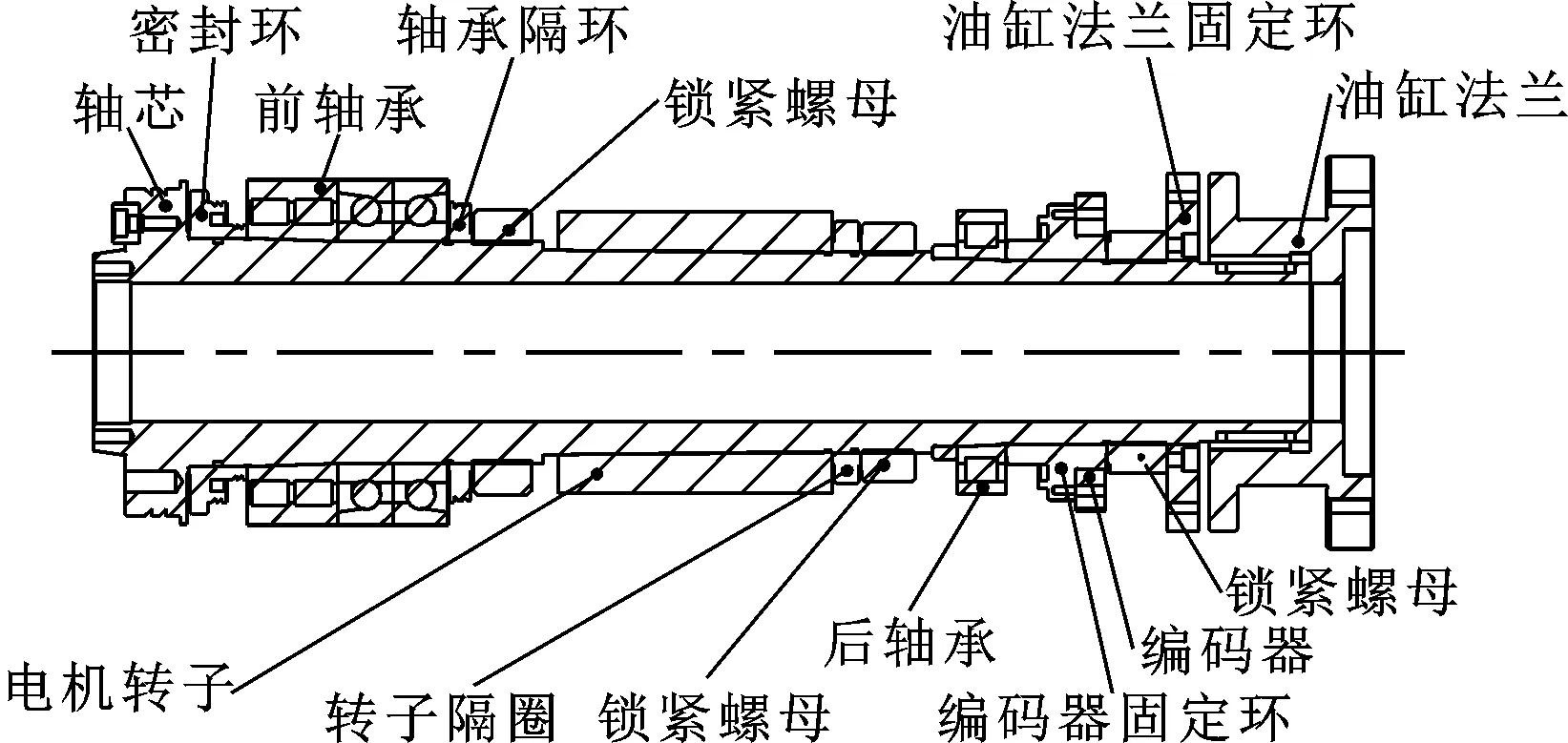
图2 某型电主轴结构示意

从简支梁模型可知，轴承处的支撑刚度对固有频率及静刚度的计算精度具有决定性作用。因此，利用主轴静刚度测试设备对该型车床电主轴进行轴向与径向静刚度测试，验证轴承处的支撑刚度。

实验测试现场如图3所示，其中：千分表4用于监测主轴轴芯径向位移；千分表7用于监测主轴轴芯轴向位移；千分表11用于监测主轴箱体轴向位移；千分表12用于监测工装轴向位移。主轴静刚度计算结果主要由监测轴芯的千分表决定，其他部位的千分表仅用于评估测试工装的刚性。

图3 某型电主轴径向与轴向静刚度测试现场

分别进行加载与卸载,重复测试3次，记录位移数值以及载荷数值, 提取规律变化明显及重复性较好的曲线数据,在Origin软件中进行加载阶段线性部分的拟合,得到主轴轴向与径向静刚度分别为378.8、478.8 N/μm，如图4所示。

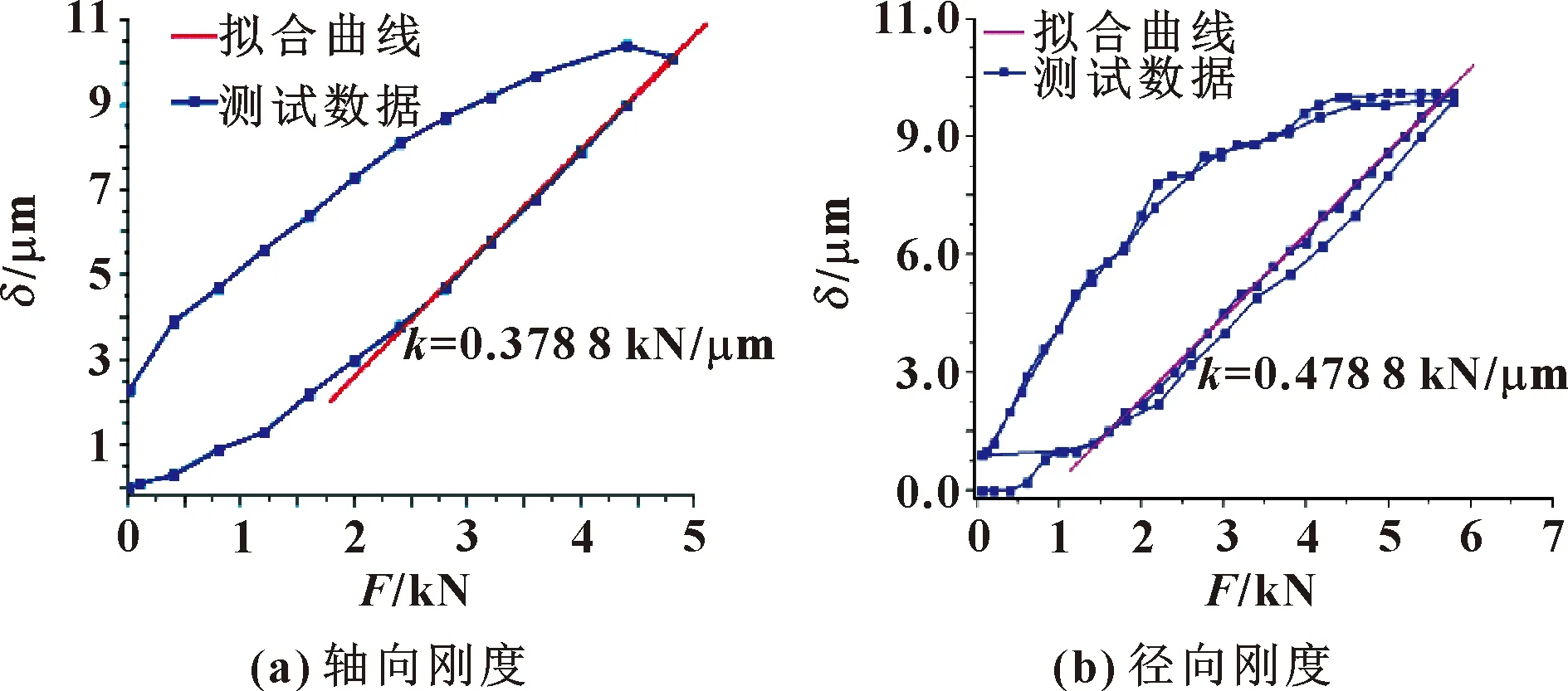
图4 某型电主轴轴向与径向静刚度拟合结果

基于上述主轴静刚度测试结果，建立有限元仿真模型。其中电机转子部分的各向异性弹性模量数值参考文献[7]进行计算。在主轴鼻端施加与实验一致的恒载荷，得到相应测点部位的变形量，如图5所示。可知：在3 000 N载荷下相应测点位移为6.1 μm，计算得到静刚度为491.8 N/μm，与实验测得的拟合结果的误差为2.7%，满足建模分析要求。

图5 某型电主轴径向静刚度仿真变形云图

3 不同跨距下固有频率与静刚度仿真计算

基于第2节中实验验证的仿真模型，建立电主轴模态分析模型及静力学仿真模型，在轴承部位施加相同的支撑刚度。由于跨距主要受电机转子长度的影响，改变电机转子长度(为保证主轴输出力矩及功率一致，相应的电机转子直径也发生变化)来达到不同的跨距设计值。基于文献[1-4]，受跨距影响明显的指标是径向1阶固有频率及径向静刚度。因此，从不同跨距的仿真模型计算结果中提取径向1阶固有频率及径向静刚度，如表2所示。

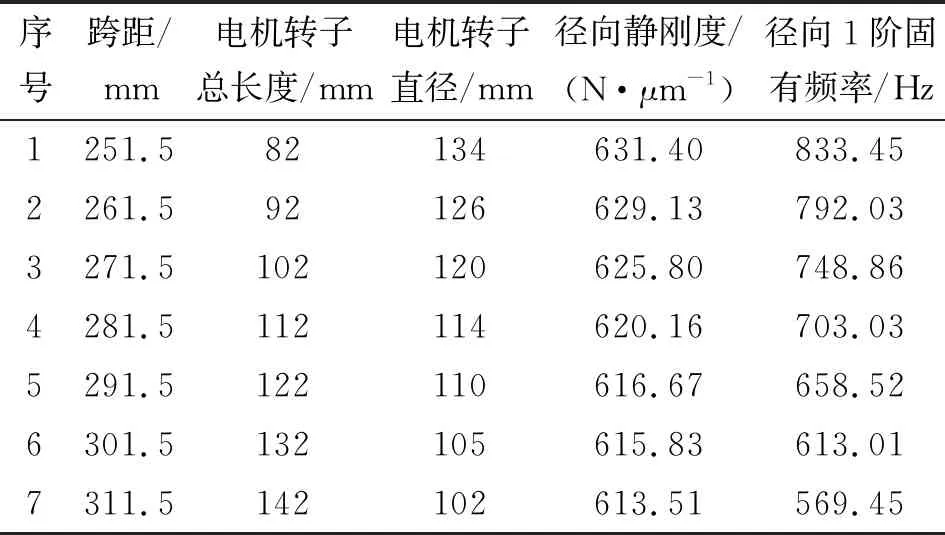
表2 某型电主轴不同跨距下径向1阶固有频率及径向静刚度

表2中序号4对应的变量为当前跨距设计方案，可以看出：随着跨距的增大，主轴径向1阶固有频率与径向静刚度均逐渐减小，但固有频率的减小幅度远高于主轴径向静刚度的减小幅度。

图6所示为跨距逐渐增大时径向静载荷下变形云图。可以看出：当跨距较小或较大时，主轴尾端变形相对偏大，而主轴前端的变形基本不发生变化，原因可能是前轴承静刚度远高于后轴承。

图6 主轴受径向载荷随跨距L增加的变形云图

图7所示为跨距逐渐增大时径向1阶固有频率对应的振型云图。可以看出:跨距变化时，振型基本不发生改变，均为轴尾的弯曲变形。

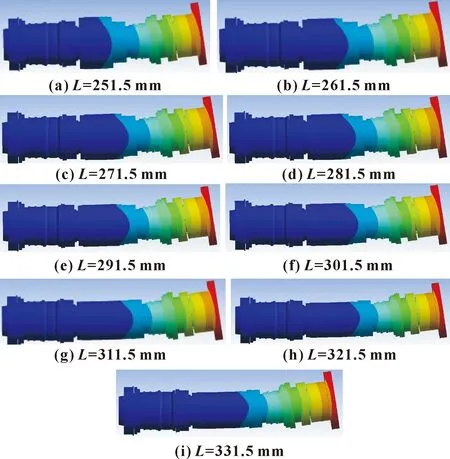
图7 径向1阶振型随跨距变化云图

结合前面最佳跨距的理论公式计算结果，可知最佳跨距296 mm处于仿真模型的中间偏后序号位置，而通过有限元仿真提取的径向1阶固有频率及径向静刚度，并不能从趋势上得到最佳跨距。从云图中只能发现轴尾变形存在一定差异，因此从静刚度仿真模型结果中提取轴尾平面的位移进行趋势分析，结果如表3所示。

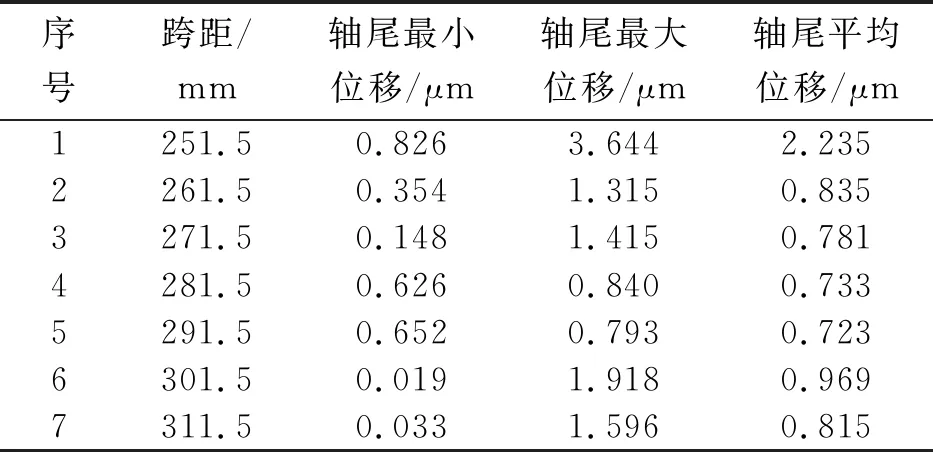
表3 某型电主轴不同跨距时静载荷下轴尾变形

从表3中可以看出:在最佳跨距计算值296 mm附近,其轴尾平均位移最小，而跨距较小时，虽然仿真提取的径向1阶固有频率及径向静刚度较高，但是轴尾的变形量偏高。因此评价电主轴最佳跨距设计时应考虑从仿真模型中提取轴尾平均位移，同时以最佳跨距理论计算公式进行迭代计算，若计算得到的数值十分接近，说明该值就是主轴的最佳跨距值。从文中所示案例来看，轴尾平均位移较小时其跨距在291.5 mm附近，与最佳跨距理论计算公式迭代得到的数值296 mm十分接近，可认为296 mm即为最佳跨距设计值。

4 结论

通过对某型电主轴跨距进行理论计算及仿真分析，得出如下结论：

(1)电主轴最佳跨距的设计可同时结合最佳跨距理论计算公式的迭代值及有限元仿真方法;采用有限元仿真方法时应将轴尾位移变化量作为评价指标之一，适用于径向1阶固有频率或径向静刚度随跨距单调变化的情况;

(2)采用有限元方法分析跨距设计值时，跨距设计值对径向1阶固有频率的影响程度远高于对径向静刚度的影响程度;

(3)车床电主轴轴芯刚度较高，区别于高速电主轴轴芯结构，两者变形形式存在一定差异;

(4)本文作者以某型电主轴为例，由最佳跨距理论计算公式迭代得到的最佳跨距为296 mm，仿真计算得到的最佳跨距为(291.5 ±10)mm，两者十分接近，可认为最佳跨距即为296 mm，可为电主轴的跨距设计提供参考。