基于液动力的水压阀阀口设计及试验研究
赵瑞豪,廉自生,廖瑶瑶,张恒,李润泽
(1.太原理工大学机械与运载工程学院,山西太原 030024;2.煤矿综采装备山西省重点实验室,山西太原 030024)
0 前言
电液方向阀是煤矿液压支架液压系统的核心控制元件。随着液压支架智能化的不断发展,支架用比例方向阀得到诸多学者的关注[1-2]。煤矿液压支架使用乳化液(95%的水+5%的乳化液)或者纯水作为传动介质,且工作流量大(≥200 L/min),阀芯所受的液动力成为比例方向阀设计中不可忽略的因素。近年来随着对水压比例阀的深入研究,非全周开口水压阀的流场分析成为了研究热点[3]。
滑阀结构和锥阀结构均是液压阀常采用的结构,滑阀在设计加工非全周节流口具有天然的优势[4],但是水介质黏度低、润滑性能差,滑阀结构的零位密封特性限制了此类阀向高压大流量的方向发展[5]。锥阀由于密封性好、抗污染能力强、结构简单等优点,在水压阀应用中非常普遍[6]。为了能设计成非全周开口,各类比例阀都对锥阀作了改进,使其成为“锥滑阀”结构,利用锥阀线密封特点保证零开口情况下无泄漏,利用滑阀结构设计合理的非全周节流口。大量的学者对此进行了研究:HAN等[7]针对大流量水压比例阀非完整阀腔阀口液动力进行了研究,通过合理设计非全周节流口尺寸减小了阀口液动力大小;LIU等[8]针对非完整阀腔提出了增加减震尾来减小阀口液动力的方法;谢海波等[9]利用CFD仿真软件研究了不同阀口形态对内流式锥阀液动力的影响。
由于“锥滑阀”结构将密封与节流两个功能分开考虑,因此存在先节流后密封和先密封后节流两种设计方案,尚没有学者对上述两种结构进行对比分析。本文作者首先建立了新型比例方向阀的数学模型,分析了液动力对比例阀性能的影响;利用CFD流场仿真软件,分析了上述两种结构中阀芯所受液动力的影响规律,并设计搭建了试验系统对仿真结果进行了验证。研究结果可为液压支架比例方向阀的设计提供参考。
1 工作原理
图1为新型比例方向阀结构和工作原理,它由主级和先导级组成。先导级由先导级1和先导级2组成,其中先导级2为由脉宽调制技术(PWM)控制的高速开关阀。主级由进、回液阀芯组成。图1所示为比例控制模式,此时先导级2先通电,PWM占空比调为1,在由先导级2和位移反馈槽组成的液桥作用下,容腔2压力为p2;先导级1随后通电,容腔1的压力升高,回液阀芯运动关闭回液口,进液阀芯在容腔2和容腔3压力的作用下不动作;容腔2的压力受控于液桥,当减小PWM的占空比,先导级2流量减小,容腔2压力随之降低,进液阀芯平衡状态被打破,开始运动并打开进液口,与此同时位移反馈槽的过流面积减小,容腔2的压力再次升高,当进液阀芯受力平衡时便不再运动;反之,当增大PWM占空比进液阀芯将会朝着关闭进液口的方向移动。

图1 新型比例方向阀结构及工作原理
根据比例阀工作原理建立其数学模型,通过先导级2流入容腔2的流量为
(1)
经过位移反馈槽流出容腔2流量为
(2)
容腔2内流量与压力变化关系为
(3)
忽略进液阀芯受到的摩擦力,其动力学方程可表示如下:
(4)
整理式(1)—(4)可得:
(5)
式中:qy为先导级2的流量;D为PWM占空比;Cy为阀口流量系数;Ay为先导级2阀口过流面积;ρ为介质密度;ps为供液压力;p2为容腔2压力;qc为位移反馈槽的流量;wc为位移反馈槽宽度;xc为矩形反馈槽初始长度;x为进液阀芯位移;V2为容腔2的体积;β为介质的体积模量;Fs为稳态液动力;mx为进液阀芯质量;Bv为黏性阻力系数;εx为进液阀芯截面积比,可用下式表示:
(6)
由式(5)可知:进液阀芯位移与PWM信号占空比成线性反比例关系。当供液压力恒定时,阀芯稳态液动力是影响阀性能的重要参数,考虑稳态液动力方向朝向阀口关闭方向,那么稳态液动力越大阀芯稳态位移越小;稳态液动力的非线性特性会影响阀芯位移的线性度,稳态液动力越大,阀芯线性度越差。相同工况下,稳态液动力小的阀口形式应当是比例阀设计的首选。
2 阀口结构及流道模型
2.1 阀口形式
稳态液动力的重要影响参数之一是阀口的结构形式。比例阀的设计整体采用“锥滑阀”的结构形式,图2所示为两种不同结构的“锥滑阀”结构示意,在先节流后密封式结构中,非全周节流口设置在阀套位置,在先密封后节流式结构中,非全周节流口设置在阀芯位置。密封锥半角选择30°和31.5°,非全周节流窗口选择为矩形,两种不同结构形式的节流口面积梯度、过流面积均设计为相同。

图2 不同“锥滑阀”结构示意
2.2 几何模型与网格划分
利用SolidWorks分别建立不同阀口开度下,两种“锥滑阀”结构的流道三维模型。图3所示为开口量为3 mm的流道三维模型。将上述两种流道模型导入ICEM软件中进行网格划分,图4为开口量3 mm时的网格模型,在阀口以及几何尺寸突变的位置进行了局部网格加密处理。

图3 开口3 mm时三维流道及流体作用面示意
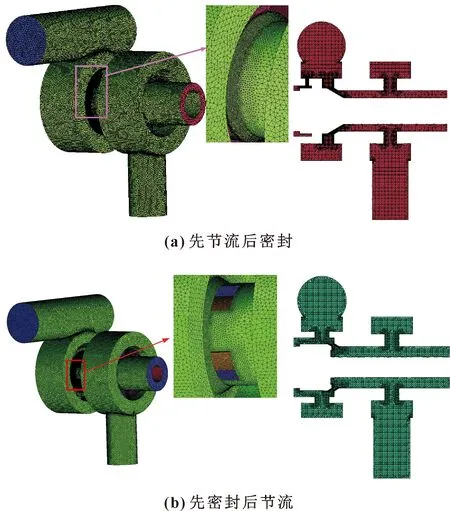
图4 开口3 mm时流道模型网格划分
3 CFD仿真研究
3.1 CFD仿真设置
液流在阀腔内部流动时,作用于阀芯的稳态液动力,一部分是以压力的形式作用于阀芯各截面,还有一部分以黏性力的形式出现。图3定义了阀芯各主要受力面,因此阀芯所受稳态液动力可由下式表示:
Fs=Fpn·a+Fvn·a
(7)
式中:Fs为阀芯受到的稳态液动力;Fpn为阀芯受到的压力;Fvn为阀芯受到的黏性作用力;a为阀芯轴向矢量分量,方向指向阀口关闭的方向。
Fluent中Standardκ-ε湍流模型计算精度高、运算量小,被广泛用于仿真液压阀内部流场问题。其中湍动能κ以及耗散动能ε由下列方程限定:
(8)
(9)
式中:ρ为介质密度;xi、xj是坐标分量;ui是速度分量;μ为介质黏度;Gκ为平均速度梯度引起的湍动能;Gb表示浮力引起的湍动能;YM代表了可压缩湍流向整体耗散率的波动扩张;C1ε、C2ε和C3ε为经验常数;σκ和σε分别为湍动能κ和耗散率ε相关的普朗特数;Sκ和Sε为用户定义的源项。湍流黏度μt用下式表达:
(10)
式中:Cμ为模型常数,仿真时采用水介质,并考虑其为不可压缩流体。C1ε、C2ε和C3ε取值为默认参数,各参数取值为:Gb=0,YM=0,C1ε=1.44,C2ε=1.92,Cμ=0.09,σκ=1.0,σε=1.3。边界条件设置为流量入口,压力出口,出口压力设置为0 MPa,阀芯最大位移量为5 mm。
3.2 仿真结果分析
流道网格数量往往会影响到Fluent求解的精确性,因此有必要对流道网格质量进行无关性检验。如图5所示,分别设置最大网格尺寸为0.8、1.0、1.2 mm,3种情况下分别监测液动力和阀口压差,对比发现最大网格尺寸设置为1.0、0.8 mm时无明显差异,且最大网格为1.0 mm时网格数量达到了370万。为兼顾计算机运算速度与求解精确性,以下的仿真均基于最大网格为1.0 mm时的模型。

图5 不同结构“锥滑阀”模型网格无关性检验
图6为在不同阀口压差和阀口开度条件下不同结构的“锥滑阀”液动力变化曲线。可知:两种不同结构的阀口液动力均为正值,即朝向阀口关闭的方向,易于阀芯稳定;当阀口开度一定时,随着阀口压差的增加,液动力单调递增;当压差一定时,随着位移的增加,液动力先增大后减小,两种结构的“锥滑阀”阀口液动力变化趋势是一致的,阀口开度在1.75 mm时达到最大;同等压差和阀口开度下,先密封后节流结构“锥滑阀”液动力的值要明显小于先节流后密封结构“锥滑阀”的液动力,出现这种现象的原因是由于锥面face2(密封面)在两种结构中分别位于节流口的下游和上游。
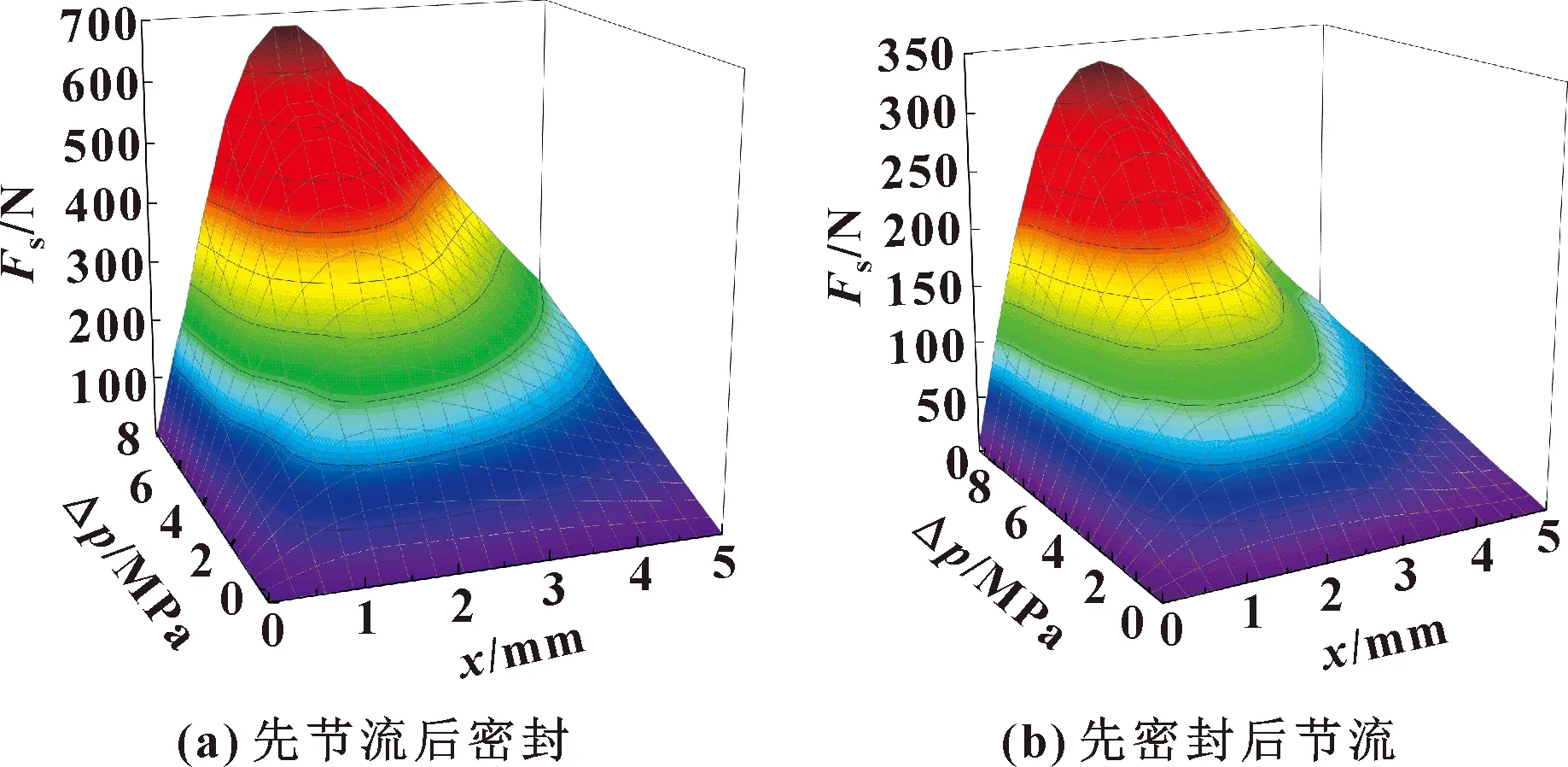
图6 不同结构“锥滑阀”液动力曲线
图7所示为入口流量为50 L/min时,两种不同结构的“锥滑阀”所受液动力以及锥面face2上的轴向作用力。同样可以看到:相同开口量的情况下先密封后节流结构阀口液动力小于先节流后密封结构的阀口液动力,随着阀口开度的增大这种差异在减小,开口量达到5 mm时,两者差距不大。对于先节流后密封结构,锥面face2位于节流口下游,作用于锥面face2的力是经过阀口节流后的低压;而对于先密封后节流结构,锥面face2位于节流口上游,作用于锥面face2的力为阀口节流前的高压;随着阀口开度的增大,阀口节流作用减小,因此二者差距也在减小。值得注意的是:先节流后密封结构的“锥滑阀”,锥面face2的轴向作用力随着阀口开度的变化方向发生了改变;先密封后节流结构的“锥滑阀”,锥面face2的轴向作用力方向不随阀口开度的变化而改变。
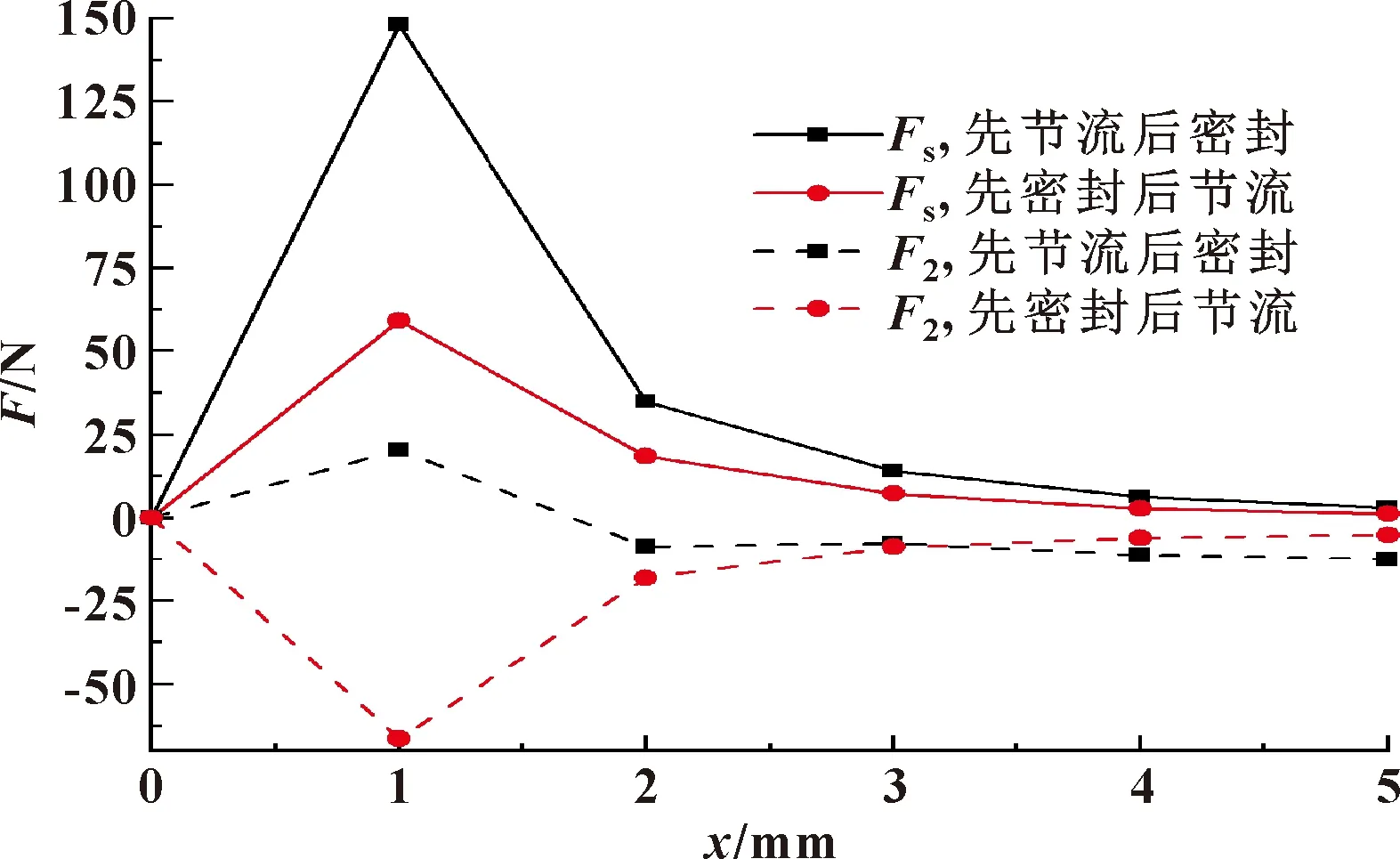
图7 阀口液动力及face2轴向力曲线
4 试验研究
油基液压阀的阀口液动力可以直接测量是因为油液黏度大,阀芯与阀套之间依靠间隙密封,且阀芯与阀套之间存在油膜,因此阀芯受到的摩擦力很小[10]。水介质阀由于水黏度小,阀芯与阀套之间通常采用密封圈进行密封,因此会引入较大的摩擦力,且这个摩擦力是非线性的、难以测量的,因此水压阀阀口液动力无法直接测量,文中采用间接的方式验证液动力的大小。
稳态液动力是液压阀内流体流动过程中没有时变流动的情况下,由于液体流动而引起的液体介质对阀芯的附加作用力[11]。因此阀芯在阀口部分受到的作用力包括液流流动对阀芯施加的反作用力和阀口压差施加给阀芯的作用力,根据比例阀流道模型可得:
Fs=-ρQv1cosα1-ΔpA1
(11)
(12)
式中:负号表示朝向阀口关闭的方向;ρ为介质密度;Q为阀口流量;v1为流入阀腔流道的流速;α1为流入阀腔流道的入射角;Δp为阀口压差;A1为face1面积;Ain为阀口过流面积。上式可以简化为
(13)
式中:Ain和入射角α1与阀芯位移相关。因此,当阀芯位移一定时,液动力的大小只与阀口流量和压差有关,因此只需将试验所得阀口流量和阀口压差与仿真对比即可间接验证阀口液动力的正确性。
图8所示为阀口液动力测试原理,动力源由泵站、蓄能器组等组成,阀芯位移通过位移平台10进行调节,阀芯通过两端螺杆进行定位,负载压力由手调溢流阀14进行调节,利用NI 6251进行传感器信号的采集。对先密封后节流的阀口形式进行了试验研究,测量了不同工况时的阀口流量和阀口压差。图9所示为试验结果与仿真结果的对比,仿真结果与试验结果相近,由公式(13)可知CFD仿真分析结果是可信的。

图8 液动力验证试验原理

图9 试验与仿真结果对比
5 结论
液动力是影响比例阀性能的重要因素,较小的液动力有利于阀芯的控制。本文作者利用CFD仿真和试验,针对“锥滑阀”先节流后密封与先密封后节流两种结构进行了阀口液动力的分析,得出如下结论:
(1)两种“锥滑阀”结构阀口液动力变化趋势相同,相同阀口开度下,阀口压差越大液动力越大;相同阀口压差下,随着阀口开度的增加,液动力先增大后减小,最大值出现在开度1.75 mm位置。
(2)相同阀口压差和阀口开度情况下,先节流后密封结构“锥滑阀”的阀口液动力远大于先密封后节流结构“锥滑阀”的阀口液动力,随着阀口开度的增加,这种差距在减小。位于节流口附近的锥面face2是造成两种结构阀口液动力差异的主要原因,先节流后密封结构“锥滑阀”的锥面face2在阀口小开度时所受轴向力朝阀芯关闭方向,随着阀口开度的增加,其所受轴向力方向发生改变;先密封后节流结构“锥滑阀”的锥面face2所受轴向力方向不随阀口开度的变化而变化。
(3)通过对液动力产生的理论分析可知:在阀口开度一定时,液动力大小只与阀口流量与压差有关。根据这一原理搭建了液动力验证试验台,先密封后节流阀口形式的试验结果与CFD仿真结果符合度较高,间接地验证了CFD仿真结果的正确性。先密封后节流的“锥滑阀”结构是水压比例阀阀口形式的优先选择,文中研究为水压比例阀的进一步优化设计提供了参考。

