基于平滑指数法的废旧零部件再制造成本预测

何钱，张旭刚，张华，江志刚

(1.武汉科技大学冶金装备及其控制教育部重点实验室, 湖北武汉 430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室, 湖北武汉 430081)

0 前言

随着经济的飞速发展，我国制造业也得到了空前的发展，大量的机电产品得到广泛的应用。机械产品的不断推陈出新，极大地满足了人们的生活需求，但也伴随着大量的不可再生资源的消耗和对环境的破坏[1]。此时，对废旧零部件进行再制造就显得尤为重要。根据废旧产品的失效特征、失效形式以及制造工艺路线判断其剩余价值，然后选择最佳的再制造、修复方案使其重新获得使用价值[2-3]。为满足经济学价值，在进行废旧产品再制造之前对其进行可再制造性分析是十分必要的，而再制造成本的预测是可再制造性分析中的重要环节[4]。经过调查分析，大量的废旧机电产品被淘汰是由于过度的使用和恶劣的工作环境导致其零部件的失效，所以根据零部件失效特征建立一种再制造成本预测模型十分必要。

在再制造成本预测方面，国内外众多学者进行了一定的研究，并取得了大量的研究成果。桑凡等人[5]分析了影响再制造成本的因素，建立了灰度理论和统计粗糙理论相结合的再制造成本预测模型；宋守许等[6]通过对机械零部件寿命周期的分析，提出了同时同态的产品设计要求，证明了主动再制造对机械全生命周期和社会效益都有实际的提高；DU等[7]从废旧零部件再制造工艺流程中材料消耗和劳动力成本的角度，对再制造成本进行了预测；王涵等人[8]从再制造成本、能量和材料消耗的角度建立了再制造的多目标优化设计模型；刘志峰等[9]构建了产品失效信息与再制造成本之间的线性回归模型；张旭刚等[10]从资源、人力消耗的角度，建立了一种基于作业动因的再制造成本预测模型；敖秀奕等[11]针对目前成本分析数据少的问题，提出了半监督学习再制造成本预测模型；赵京菊等[12]从零部件寿命周期的角度提出了再制造成本预测的改进方法；向红等人[13]通过对再制造成本的分析，提出了一种再制造成本多维预测模型。

以上研究中，从技术、经济、环境以及再制造工艺流程和生命周期等方面展开了再制造成本预测的研究工作，但从失效特征的角度对废旧零部件再制造成本进行研究的较少。俞超等人[14]虽然通过再制造成本的构成，建立了零部件失效特征与再制造成本之间的预测模型，但该模型算法结构复杂、参数众多。因此，本文作者从废旧零部件失效特征的角度，通过废旧零部件失效特征检测，将失效特征进行区域量化并归一化为一个[0,1]之间的标量，通过与已完成再制造的样本数据库数据进行欧氏计算，得出相似度最高的前3组数据，采用平滑指数法对再制造成本进行预测。最后，采用平滑指数法对废旧车床C6140再制造成本进行预测，并将预测值与实际值进行比较，说明了该模型有较好的预测效果和泛化能力。

1 基于平滑指数法的再制造成本分析

1.1 预测模型

在当今机械产品大量报废的情况下，废旧产品的循环再利用显得尤为重要。然而，导致机械失效的因素有很多，即使同一型号的机械设备或者零部件在不同的工作状态下其失效特征也各不相同，从而使再制造成本有较大的差异，在进行再制造之前对废旧零部件进行失效检测十分必要[15]。本文作者在零部件失效特征分析的基础上采用了平滑指数法，通过高维空间映射求解相似度[16]，结合专家评价给定平滑系数，提高了对待再制造产品的再制造成本的预测精度。废旧零部件的再制造成本预测模型框架如图1所示。

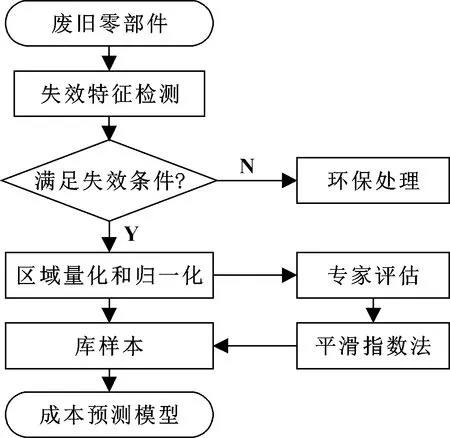
图1 废旧零部件成本预测模型框架

在进行再制造之前，对其失效特征进行检测和合理的评估十分必要，将检测到的数据进行合理的量化和归一化是进行再制造成本预测的前提和基础。根据零部件实际运行状态，采用专家模型对归一化的失效特征数据进行定量与定性分析以获取平滑系数区间。然后，依托专家平滑系数区间将废旧零部件失效特征数据与历史再制造数据进行高维空间相似度计算，实现废旧零部件再制造成本预测，同时调整平滑系数大小能够有效提高预测模型精度。

1.2 失效特征的量化和归一化

由于机械设备工作的环境和工况不同，失效特征也不尽相同。通过统计分析，机械零部件的失效形式主要有磨损、断裂和变形3种，而这3种形式的失效导致机械设备不能完成预定功能的比率高达75%以上[14]。根据设备的工况和工作环境的不同，相同设备的各零部件其失效特征和失效程度也不尽相同。在经过废旧机械前期的回收、拆卸、清洗等工序之后，采用现有的检测技术对不同零部件的失效特征进行有效的检测。由于失效特征的性质和单位不同，无法直接进行比较，必须要先进行区域量化和归一化处理，将其转换为一个标量，使其具有可比性，归一化后的数据再与数据库数据进行比较得到高维空间的相似度。

传统上对失效特征的描述过于模糊，导致对其再制造成本的预测存在很大的随机性。在实际的再制造过程中，需要根据专家评估对失效特征进行合理的区间量化，对超出可再制造阈值的废旧零部件进行绿色环保处理，将可再制造零部件的失效特征数据进行归一化处理，并在高维空间进行相似度计算，即计算其欧氏距离，欧氏距离越小表示其相似程度越高，反之则相似程度越低。最后结合专家评估对平滑系数的选取，完成对废旧零部件再制造成本的预测。文中以轴类零件为例[17]，对其失效特征进行区间量化和归一化，采用线性变换的方法归一化各损伤区间，将损伤程度转换[0,1]之间的量值，如表1所示。

表1 某零件失效特征区域量化与归一化

表1主要展现了3种失效特征不同失效程度所对应的区域量化和归一化处理结果。以某零部件的磨损量为例，当0≤ua<1.0 mm3时，此时零件为轻微磨损；当1.0 mm3≤ua<2.0 mm3时，此时零件为重度磨损；当ua≥2.0 mm3时，此时零件为严重磨损，经过专家系统评价对严重磨损的零部件将进行环保处理。数据的归一化处理是根据具体的失效程度将数据归一化为[0,1]之间的数值，便于比较和计算。将失效程度轻微的量化到(0,0.5)区间，一般程度的量化到[0.5,1)，失效严重的量化为1。以同样的方法对失效形式为裂纹和变形的失效数据进行相应的处理，具体如表1所示。

1.3 再制造成本预测

将已回收的废旧机械进行前期的拆卸、清洗等处理后，为了降低检测过程中再制造成本的增加，首先对整机进行失效分析，并获取主要失效零部件和失效特征。对导致失效且有重要经济价值的零部件进行失效检测，用ua、ub、uc分别表示磨损量、裂纹量和变形量，归一化后用xa、xb、xc表示，用M=[xaxbxc]表示零部件的失效特征向量。对已完成再制造的零部件数据建立一个样本数据库L={(M1，C1)、(M2，C2)、…、(Mn，Cn)}，其中Mi表示已完成再制造失效特征数据，Ci表示对应失效特征的再制造成本。通过高维空间中的映射，将待再制造数据遍历样本数据库，并对其求高维空间中距离，距离用di表示。

di=|M′-Mi|

(1)

C′=α·C1+α·(1-α)·C2+α·(1-α)·

(1-α)·C3

(2)

式中：C′表示待再制造零部件的再制造总成本；C1、C2、C3分别表示相似程度最高的3组数据的再制造成本；α表示平滑系数。使用平滑指数法预测再制造成本时，平滑系数的选择至关重要，直接影响到预测精度。

传统上平滑系数一般采用经验准则法、自适应选取法、0.618优选法等多种方法确定。文中综合专家系统和自适应性法选择平滑系数，这种选取方法既包含了专家来自于实践的经验，同时又兼顾实际参数的随机性，更好地提高了平滑指数法对零部件再制造成本的预测精度。平滑系数α为一个[0,1]之间的数值，在专家系统的基础上，采用自适应选取法，即从[0,1]之间依次选取1 000个数字进行模拟，再由专家指导选择再制造成本预测精度最高的平滑系数。

1.4 流程算法及具体步骤

平滑指数法不仅模型简单、计算过程简洁，而且有着较强的数据处理功能，通过改变平滑系数的大小能够有效地提高预测值的精度，该模型的具体算法流程如图2所示。文中综合使用了专家评价系统和自适应性法，既增加了数据处理过程中专家的经验指导，同时也加入了对单纯数字分析时的随机性。使用已完成再制造产品的数据建立一个样本数据库，完成对待再制造产品失效特征的检测，将其与数据库样本数据进行欧氏距离的计算，通过欧氏距离反映失效特征间的相似程度，将相似度最高的3组数据取出，采用平滑指数法对待再制造产品的再制造成本进行预测。

图2 模型算法流程

具体步骤如下：

(1)建立样本数据库。通过对少量已完成再制造的废旧零部件失效特征数据和再制造成本进行收集整理，得到样本数据库L={(M1，C1)、(M2，C2)、…、(Mn，Cn)}。

(2)检测待再制造零部件失效特征。通过对废旧零部件的整机分析，在考虑经济条件的情况下，对导致失效的主要零部件进行必要的检测，采用现有检测技术对废旧零部件的磨损量、裂纹量和变形程度进行检测。

(3)失效特征的区域量化与归一化。对严重失效的零部件进行绿色环保处理，对还有剩余使用价值的零部件归一化处理，便于后期比较和计算。

(4)相似度计算并排序。在高维空间中求归一化后的数据与样本数据库数据的欧氏距离，通过欧氏距离进行相似度排序，即距离越远相似度越低，反之则相似程度越高，并按照距离由小到大进行排序。

(5)平滑系数的选择。在专家系统的基础上，采用自适应性法计算平滑系数。在再制造成本预测中依次增大平滑系数值并计算，找到最佳的平滑系数。最佳平滑系数的选取可以通过程序算法来实现。

(6)再制造成本计算并检测。通过相似度的排列，选取相似度最接近的前3项，采用平滑指数对其再制造成本进行求解，并采用测试样本进行检测。

2 案例及结果分析

机床是工业生产中重要的设备之一，随着科技与社会的不断发展，机床生产强度不断加强，同时也加快了机床报废速度。文中以废旧车床C6140为研究对象[17]，通过整机分析可知其主要失效零部件为轴类零件蜗轮蜗杆；通过对蜗轮蜗杆进行失效特征检测，将其主要分为磨损、裂纹和变形；根据蜗轮的工作特点将磨损分为平面磨损、齿面磨损、齿面疲劳磨损、外锥面磨损和自由曲面磨损，裂变分为齿面裂变和齿根裂变，蜗轮在工作中主要的变形是蜗杆变形，具体信息可参照表2。

表2 废旧车床的主要信息

将10组已完成再制造的数据建立数据库，使用5组已知的再制造成本的数据采用平滑指数法对其进行再制造成本预测。数据库和已知的再制造成本的数据如表3、表4所示。

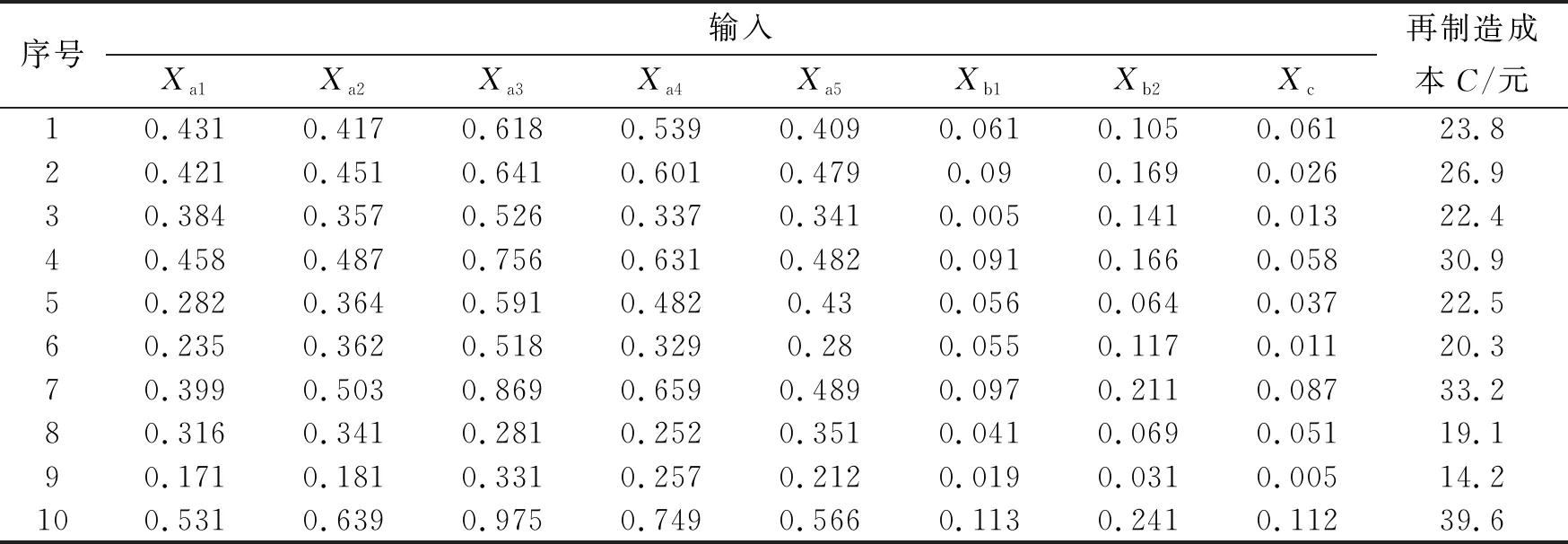
表3 数据库样本数据

表4 已知的再制造成本数据

2.1 参数的选择

对废旧零部件再制造成本的预测主要采用平滑指数法，其中平滑系数α的选取至关重要，直接影响到预测精度。为了提高预测精度和预测模型的灵敏度，在选取平滑系数α时，在专家评估指导的基础上采用自适应性选取法，在[0,1]区间上采用逐渐增大、逼近最佳系数的原则。这种方法不仅综合了实际生产过程中历史经验和对原始数据的数值分析，更提升了模型的运算效率。使用上述方法选取的平滑系数α=0.77，将归一化后的失效特征数据进行欧氏距离计算，即相似度计算，完成对待再制造废旧零部件的再制造成本预测。

2.2 预测结果与分析

采用平滑指数法对废旧零部件再制造成本进行预测。这种方法结构简单、计算量较小，而且预测精度较高能满足一般的企业需求，为再制造企业提供一种便捷的再制造成本预测模型。为了体现平滑指数法的可行性和优越性，这里采用均方误差e来衡量预测性能。

(3)

表5 实际值与预测值比较结果

由表5可知：采用平滑指数法对废旧零部件进行再制造成本预测时，由于在选取平滑系数过程中综合了专家评估和自适应性选取法的优点，使得预测结果十分准确，最大误差为5.82%、最小误差可达0.60%、平均误差仅为2.62%、预测的均方误差e=0.79，很好地显示了平滑指数法的准确性和泛化性能。

3 结论

针对废旧零部件的再制造成本预测问题，提出了基于平滑指数法的废旧零部件再制造成本预测方法，通过对整机失效分析得到主要失效零部件和失效形式，采用区域量化和归一化的方法对失效特征数据进行处理，遍历数据库数据进行相似度计算，结合专家评估和自适应性选择最佳的平滑系数。最后，以废旧车床C6140的再制造为例，采用平滑指数法对废旧零部件再制造成本进行了准确的预测，验证了该方法的有效性。该方法算法结构简单、计算量小，并结合了经验丰富的专家评价系统和对原始数据分析的自适应性选择，在一定程度上满足了一般再制造企业对废旧零部件再制造成本进行快速判断并做出决策的要求。因为样本数据库数据较少，导致采用平滑指数法对再制造成本预测精度还有待进一步提高。

失效特征只是导致机械零部件失效的一个方面，影响零部件失效的因素众多，如环境因素、材料因素、实际工作载荷等。该模型依然对历史数据的依赖程度很高，然而对于历史数据的获取在一定程度上又有一定的难度，并且这还为零部件整体设计再制造过程增加了一定的成本。未来将致力于针对待再制造机械的历史维修数据、实际使用工况和材料性能等进行分析，研究其再制造成本预测方法。