基于流固耦合的供水管道的振动特性分析

李明华，冯佳荟，韩雯静

(南昌交通学院土木建筑学院，江西南昌 330013)

0 前言

由于压力管道的安全性和经济实用性较高，可将它应用于燃气、输水等领域。管道系统在工作过程中会产生流量脉动和压力脉动，引起严重的管道振动[1]；异常或者过度的振动将会引起管道共振，引发管道破裂、腐蚀和其他安全问题。下穿铁路桥梁的供水管道由于受列车经过时产生的较大振动作用，容易发生弯曲和扭转，严重情况下会与列车经过时产生的振动频率发生共振现象，造成管道破裂、路基不夯实和轨道下沉等现象。

钱继春[2]采用功率谱分析、相干分析的办法对高层供水系统动态特性进行初步分析和减振降噪研究，对管道系统的结构特性进行了有限元分析，从而实现管道结构减振降噪的目的。闫彩云等[3]在充分考虑不同约束、不同管径、不同壁厚和不同材料损耗因子等因素后，通过建立模型研究管道对供水管道振动与噪声辐射特性的影响。赵信智和白双宝[4]使用ANSYS Workbench，从管道支撑结构管夹间距布置、管道壁厚及内流体流速对管道振动影响的角度进行了仿真设计，对液压管道进行流固耦合振动分析。干梁[5]以某型民机废水管路系统为研究背景，采用有限元法仿真分析管道在周期脉动流作用下的单双向流固耦合动力学特性及气液两相流作用下的动力学响应。周知进等[6]利用有限元方法，研究了流固耦合作用下不同曲率管道的等效应力、位移变形和流体流动特性规律。赵江等人[7]针对由流体引发的T形管振动问题,采用基于双向流固耦合的模态分析方法,对流体作用下的T形管模态进行分析，在双向流固耦合基础上分析流体压力、流体速度和流体密度对管道固有频率的影响。钟永恒等[8]基于特征线性方程模型,对充液管路系统中弯头处的流固耦合进行了建模研究,得出了弯头处的平衡方程及弯头对管道流固耦合振动特性的影响，验证了所建模型的正确性。郑瑞[9]对管道进行流固耦合模态分析,研究了管道长度、管道形状及管道材料对其固有频率的影响。夏永胜和张成龙[10]以噪声试验台液压系统的折弯式管道为例,采用ANSYS Workbench进行有限元联合仿真,研究了流固耦合作用对管道振动的影响。

国内外学者对管路流固耦合的特性已有一定的研究，并取得了丰硕的成果，但是目前尚未查到针对下穿铁路桥梁供水管道的文献。供水管道下穿铁路桥梁时，需要考虑列车经过铁路路基时的共振与压力脉动突变的问题。本文作者首先建立国内某段下穿铁路桥梁的供水管道的模型，基于所建立的模型的管道和流体部分分别进行网格划分；利用Workbench软件进行流固耦合模拟；在单向流固耦合的基础上分析流体的速度、密度和管径厚度对管道固有频率的影响。

1 流固耦合数值模拟理论分析

1.1 管道的流体运动分析描述

流固耦合问题是流体力学与固体力学交叉而生成的力学问题。在分析流固耦合问题时，既要分析流体运动，又要分析固体的形变，是从流体力学N-S方程和固体力学小变形弹性理论导出的求解流固耦合(Fluid-Structure Interaction，FSI) 的基本方程，流体控制方程和固体控制方程均可满足，且流体流动计算符合质量守恒及动量守恒方程。对于一般可压缩的流体，其控制方程[9]如下：

质量守恒方程：

(1)

动量守恒方程：

(2)

式中：t表示时间；ff表示体积力矢量；ρf表示流体密度；v表示流体速度矢量；τf表示剪切力张量。

在柱坐标系下流体的连续性方程为

(3)

管道轴向方向的运动方程：

(4)

管道横向方向的运动方程：

(5)

式中：fr表示横向体积力密度;fz表示轴向体积力密度;vr表示流体横向速度矢量；u为管道的运动速度。

1.2 湍流模型

在下穿铁路桥梁的供水管道试验中，流体的雷诺数较大，可视为湍流流动。在数值计算中，选择标准κ-ε模型作为流动方程，表达式[11]为

κ方程为

(6)

ε方程为

(7)

式中：Sε、Sκ表示湍能耗散率及湍动能的源项；C1、C2、C3表示设定的经验系数;YM表示可压缩流体中脉动扩张量;Gb表示由于浮力引起的湍动能κ的产生项；Gκ表示由于速度梯度所引起的κ的产生项。

1.3 液压管道流固耦合的边界分析

液压管道中的流体及管道壁接触，从而产生相互作用，在忽略管道径向惯性作用力对管道运动的影响，同时不考虑离心力和哥氏力对管道轴向运动的影响时，分析得出管道和流体的流固耦合振动方程。

液压管道内流体轴向方向的流动方程：

(8)

液压管道轴向方向的运动方程：

(9)

式中：vf为流体流动的平均速度；ρp为管道的密度；δ为管壁的厚度；τw为管道内部的流体和管道之间的摩擦力。

2 管道的几何模型及模态分析

2.1 几何模型

选择国内某段下穿铁路桥梁的供水管道作为研究对象，管道的三维图形和中间截面剖面分别如图1和图2所示。管内径为100 mm，管道壁厚5 mm，AB=300 mm，BC=3 000 mm，BD=300 mm；A为进水口，D为出水口。

图1 供水管道三维模型

图2 管道几何结构示意

2.2 模态分析

模态是结构系统的固有振动特性，每阶模态都有对应的固有频率和振型。对供水管道的三维模型进行网格划分，将管道外部和管道内部的膨胀层分别划分为固体网格和流体网格，采用四面体网格划分模式，如图3所示。利用ANSYS Workbench的Modal和Fluent模块对供水管道的流体动力学和自由状态下的模态进行计算，同时，对供水管道的外壁面和流体域(膨胀层)进行单向流固耦合分析，流体计算结束后利用Transient structure和Modal模块，将计算得到的流体域载荷加到供水管道的内壁面上，求解瞬态结构动力学耦合计算下的模态，计算流程如图4所示。在计算过程中，定义管道的材料为Q235B，其主要参数为密度7 800 kg/m3、弹性模量201 GPa、泊松比0.3。为研究下穿铁路桥梁供水管道的动态特性，设置管路的入口和边界条件为压力入口、出口边界条件设置为压力出口；湍流模型选择RNGκ-ε模型，壁面采用无滑移面，计算过程中不考虑传热效应；根据现有供水管道的技术标准[12]，设置供水管道的进水口流速为4 m/s、压力为5 MPa。供水管道内自来水的密度为1.225 kg/m3，将收敛精度设定为0.01、迭代步数为100，迭代数据每步保存一次，然后进行初始化并求解，残差曲线如图 5所示。

图3 供水管道的流固耦合网格划分

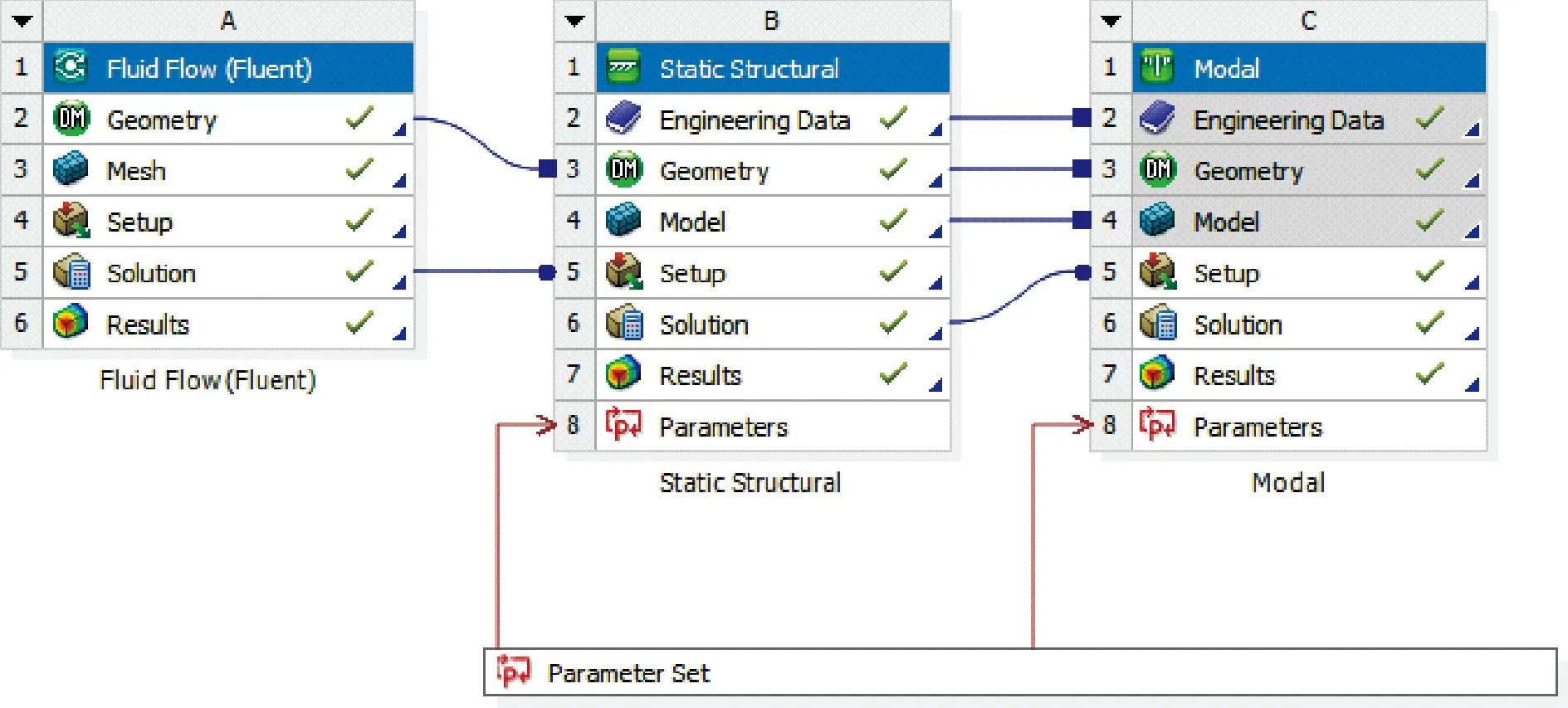
图4 流固耦合计算流程

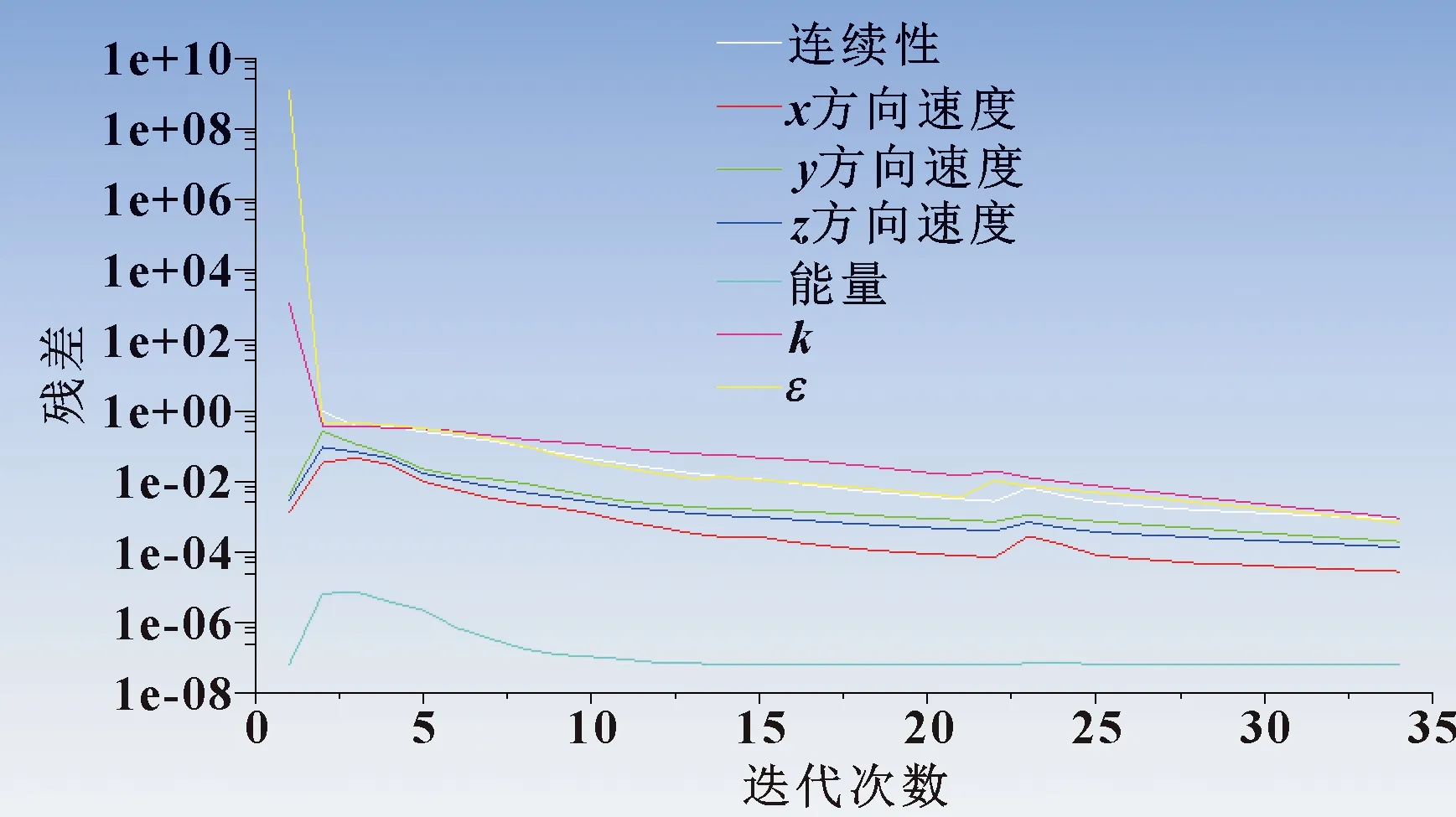
图5 残差曲线

3 试验仿真

3.1 供水管道单向流固耦合作用下的速度和压力云图分析

通过图6和图7可以看出：供水管道内的水流速度最大达到了3.813 m/s，水流速度沿着管道中心轴线的位置对称分布，水流的流速呈现一种螺旋式环绕趋势，在管道的弯曲处会出现紊流现象；管道内的压力在水流入口处呈现较大值，管道弯曲处的压力分界面呈现弯曲的状态，说明水流在管道的弯曲处会产生较大的波动效果。因此，在管道的设计过程中，应重点考虑管道弯曲接头处的压力作用。

图6 供水管道速度云图

图7 供水管道中间位置的压力云图

3.2 供水管道在自由状态和单向流固耦合作用下的固有频率分析

由表1可以看出：供水管道在流体的作用下，其固有频率受到较大的影响，管道前6阶固有频率和单向流固耦合作用下的固有频率相差不大，差值最大达到了1 Hz，不超过2%；管道6阶到10阶的固有频率和单向流固耦合作用下的固有频率相差较大，特别是7阶和9阶时，固有频率相差达到了8%～10%，这是因为管道在流固耦合作用下，水流的速度和压力对管壁产生了冲击作用，得到的管道预应力比较大，造成固有频率存在较大的差异。

表1 不同方式下供水管道的固有频率 单位：Hz

3.3 供水管道在自由状态和单向流固耦合作用下的振型分析

在进水口速度均为4 m/s的情况下，分析管道自由状态和单向流固耦合下的变形，得到管道在不同情况下前6阶的振型如图8、图9所示。由图8、图9可以看出：管道在自由状态下最大的变形量0.429 m，比单向流固耦合作用下的变形增加了5%；管道出水口附近的变形量较大，出水口弯管接头附近的变形呈现突变状态；观察管道单向流固耦合的4～6阶振型发现，在管道BC段的位置出现了变形量较大的球状区域，可能是因为管道BC段发生了弯曲，水流经过BC段区域时出现局部脉动压力，对管道产生一个较大的局部应力，产生了变形量较大的区域；随着管道变形量增大，流动侵蚀加剧，由于长时间处于高应力条件下，容易导致管道壁面侵蚀、焊缝开裂、寿命减少。

图8 不同计算方法的1～3阶振型

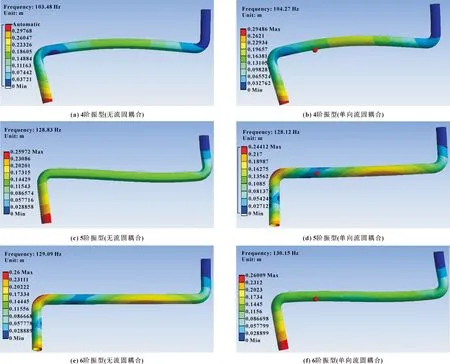
图9 不同计算方法的4～6阶振型

4 结论

本文作者以下穿铁路桥梁供水管道为研究对象，基于流固耦合的分析方法，采用RNGκ-ε的湍流模型，分析管道的速度和压力分布情况；对比管道在自由状态下和单向流固耦合作用下的固有频率和振型。结果表明：管道内的水流速度沿着管道中心轴线的位置对称分布，水流的流速呈现一种螺旋式环绕的趋势，在管道的弯曲处会出现紊流现象；管道在自由状态下和单向流固耦合作用下的固有频率相差8%～10%；管道在自由状态下最大的变形量为0.429 m，比单向流固耦合作用下的变形增加了5%；观察管道单向流固耦合的4～6阶的振型发现，在管道BC段出现了变形量较大的球状区域，可能是BC段发生了弯曲，水流经过该区域时出现局部脉动压力，对管道产生一个较大的局部应力，因此产生了变形量较大的区域；管道变形量增大，导致流动侵蚀加剧，而管道长时间处于高应力条件下容易发生壁面侵蚀、焊缝开裂，使得使用寿命减少。