小天体导航陆标深度学习预测框匹配算法
肖 扬,李 帅,王光泽,邵 巍,姚文龙
(青岛科技大学 自动化与电子工程学院,青岛 266100)
引言
近些年来,小天体着陆和采样返回任务成为研究热点,因其具有重大的科学意义和工程价值[1-3]。利用陨石坑、岩石等自然陆标是实现探测器自主导航的一种重要手段。但与火星、月球不同,小天体具有暗弱不规则、地表特征复杂和先验信息匮乏等特点,使得导航陆标的提取和匹配存在一定的困难[4-7]。
近年来,为满足图像处理问题的各类需求,以卷积神经网络为代表的深度学习理论取得不断突破。深度学习在特征提取与图像识别方面有巨大的潜力和优势,在轨道交通、生物医药、经济金融、工业生产及自动驾驶等领域得到了广泛应用。基于深度学习的导航陆标检测方法比传统的图像处理算法具有更高的识别率[8]。Emami等[9]利用Faster R-CNN网络实现了对陨石坑的自动识别。Wang等[10-11]利用U-net开发的DeepMoon网络对识别陨石坑的圆心和半径进行了标记。Lee等[12]同样采用U-net网络结构对陨石坑进行了检测,并结合数字地形模型(Digital Terrain Models,DTM)数据克服了光照等因素对检测结果的影响。Chen等[13]提出了能同时识别陨石坑、沟谷等多个特征的高分辨率模型,并利用迁移学习解决了数据缺失的问题。郑磊等[14]利用改进的非极大值抑制的深度学习算法在其构建的大型陨石坑数据集上实现了多尺度多分类陨石坑自动识别。Furlán等[15]提出了一种使用卷积神经网络(Convolutional Neural Network,CNN)检测岩石的方法,提高了分割图像的速度并取得了较好效果。Li等[16]基于U-net网络,结合视觉几何组及残差卷积神经网络,对岩石进行了检测。基于视觉的探测器自主导航是深度学习网络估计方法最有潜力的关键领域之一,通过从已有数据中自动地学习各种地形深层特征,并对导航陆标进行准确的分类识别,具有较高的准确率和鲁棒性,因此适合在小天体未知复杂环境的精确附着探测任务中应用,是未来自主导航技术潜在的替代方案[17]。
基于深度学习的识别算法给小天体导航陆标的识别提供了新思路,但对于视觉导航来说还需完成识别结果的匹配。目前相关匹配算法在应用于探测器绝对导航时还有局限性[18-21]。Danelljan等[22]在滤波器的跟踪框架下设计的多域网络(MultiDomain Network,MDNet)结构提高了目标的跟踪性能,但算法适用于序列图像间的跟踪,在绝对导航中效果不佳。Held等[23]提出基于回归网络的通用目标跟踪算法(Generic Object Tracking Using Regression Networks,GOTURN)提高了匹配速度,加入CIR单元模块增强了匹配精度。Danelljan通过训练基于尺度金字塔表示的双滤波器实现复杂序列图像中平移跟踪和尺度跟踪,但仅在相对导航中目标运动模糊、光照变换下具有好的跟踪效果[24]。Zhou等[25]提出一种新的基于Transfomer的结构用于全局多目标跟踪,搭建的网络可以直接从32帧的图像中学习匹配结果,并不是逐帧匹配。Possegger等[26]提出统计颜色特征方法,减小了边界效应并能实现快速运动目标的跟踪,但不适应存在光照变化和背景相似颜色的目标。综上所述,现有算法是基于序列图像的匹配且在旋转、光照、尺度变换下鲁棒性较差,影响导航陆标的匹配率,因此难以实现探测器的绝对导航。
为实现小天体附着过程的高精度自主视觉导航,克服现有算法在绝对导航需求中的局限性,提出一种基于特征描述符的识别预测框匹配算法。在小天体的精确附着探测过程中应用深度学习网络识别未知自然陆标,针对识别结果选取支撑区域,求取区域像素梯度构建不变性特征描述符,通过阈值限制实现识别结果的匹配,在光照、尺度及旋转变换下分析实验结果并对文章进行总结。
1 深度学习陆标识别
在探测器自主导航任务过程中采用YOLOv4网络对小天体导航陆标识别[27]。通过局部方差均衡算法增强图像中陨石坑、岩石和沟壑等地形特征,并采用透视变化等多种数据增强方法构建小天体表面地形特征基准数据集和自适应切分图像检测方法解决小特征漏检问题,结合小天体自身特点采取深度学习算法实现对小天体导航陆标的智能识别。小天体导航陆标智能检测算法的识别结果如图1所示,该算法能够更好地完成小天体导航陆标的检测任务,小天体导航陆标的识别率达到86.75%。
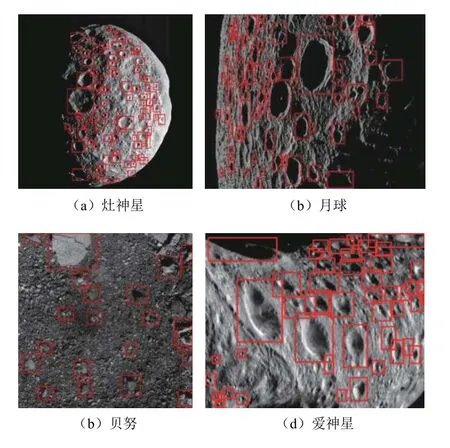
图1 小天体导航陆标检测结果Fig.1 Detection results of small celestial navigation landmarks
2 预测框描述符
导航陆标识别结果以矩形预测框形式输出,利用图像像素信息构建预测框特征描述符。预测框描述符(Prediction Frame Descriptor,PFD)的建立,采取一种在圆形支撑区域内划分梯度方向区间构建归一化描述符的方法,构建流程图如图2所示。

图2 预测框描述符构建流程图Fig.2 Prediction box descriptor build
2.1 支撑区域建立
针对着陆过程中可视区域逐渐变小造成的图像尺度变化,对图像进行降采样和高斯模糊来构建尺度空间金字塔,如图3所示,通过模拟图像数据的多尺度特征,对金字塔中每幅图像的预测框描述,以保证构建的描述符具有尺度不变性。降采样因子为以此保证在空间的连续性。输入图像大小与高斯金字塔层数关系为
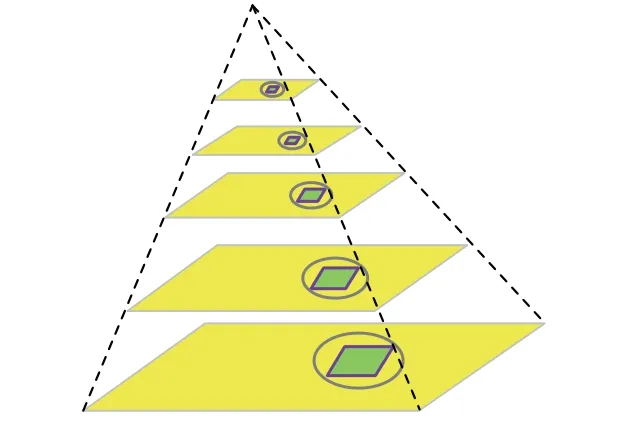
图3 预测框高斯金字塔Fig.3 Prediction frame gauss pyramid

其中:width、height分别为原图像的尺寸;min()为选取原图像宽和高的最小值。

描述符支撑区域的选取影响预测框匹配率和匹配速度。若选取矩形预测框作为支撑区域,当图像发生旋转变化后,预测框内的信息将会发生变化,如图4(a)所示。通过等比例扩大支撑区域构建描述符提高预测框匹配率,但同时也提高了算法运算复杂度,如图4(c)所示。因此采用圆形支撑区域代替矩形区域,增强了特征区域旋转变换的鲁棒性,降低了构建描述符的运算复杂性,如图4(c)所示。

图4 支撑区域选取Fig.4 Support area selection
2.2 主方向确定
计算支撑区域内像素点(x,y)的梯度幅值m(x,y)及方向α(x,y)。支撑区域中靠近中心的像素具有更高的权重,因此采用高斯模板进行权重赋值,梯度计算如图5所示。高斯函数在取权重时采用式(2)所示二维正态分布形式,即

图5 支撑区域梯度计算Fig.5 Support zone gradient calculation
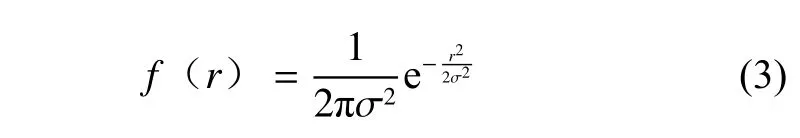
其中:r为支撑区域内像素点(x,y)到圆形支撑区域圆心的距离。
将支撑区域内的像素点按其梯度方向划分为n个区间,如图6所示,按照划分的梯度方向对各区间内像素点梯度幅值进行求和并统计梯度直方图。对于第Fi个方向区间梯度幅值求和表示为
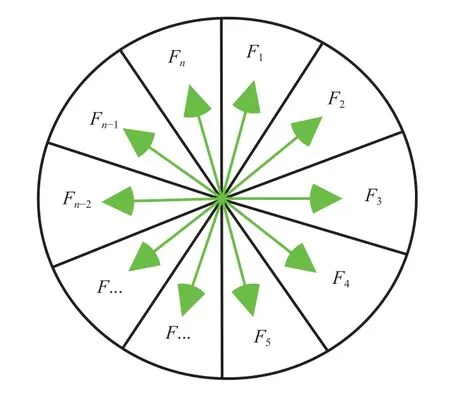
图6 支撑区域梯度方向划分Fig.6 Gradient direction division of support area
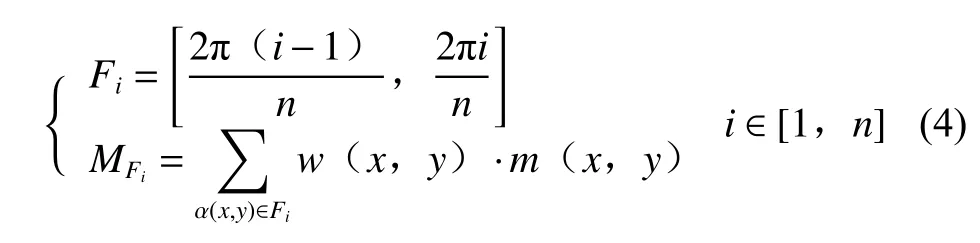
其中:w(x,y)为像素点(x,y)对应的权重系数。横轴为所划分的n个梯度方向区间,纵轴为对应方向区间内梯度幅值总和,如图7所示。
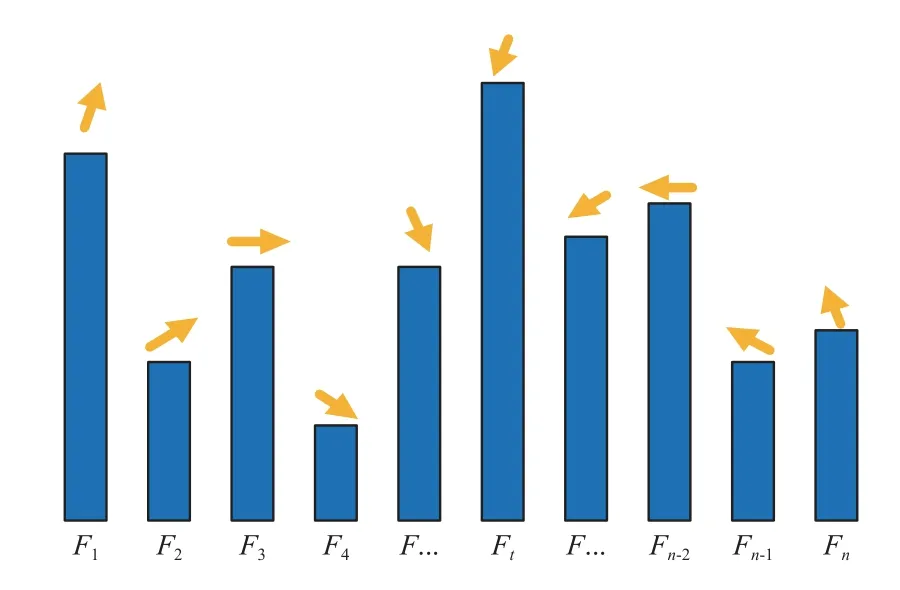
图7 支撑区域梯度直方图Fig.7 Histogram of gradient in support region
2.3 描述符生成
梯度直方图的峰值代表了预测框的主方向,并以此方向作为起始区间遍历所有区间构建描述符。描述符的向量表达式中第一个元素为主方向所在区间,其
他区间按照顺序进行排列。对应描述符可表示为

其中:第Ft区间为主方向区间。
为保证特征描述符具有整体亮度不变性,对描述符D进行归一化处理。令D中元素最大值为Mmax,最小值为Mmin,则归一化后描述符可表示为
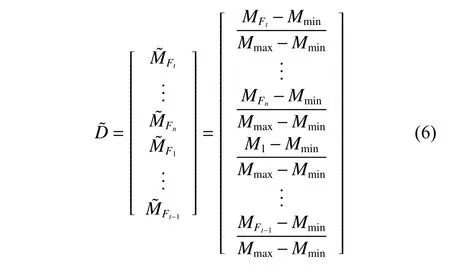
根据划分区间生成生成具有尺度、平移旋转、光照不变性的n维预测框描述符。针对描述符最优维数的选取问题,在后续3.1节中通过实验进行选取,最优参数选取为10。
2.4 描述符的匹配
为提高正确匹配率,通过计算两描述符向量间相对距离对匹配效果进行衡量。对描述符进行匹配时,若其最近邻描述符为判断匹配成立条件为

其中:参数γ 为描述符相对距离的阈值。
3 仿真验证
3.1 参数选取
为验证不同支撑区域选取范围、划分梯度区间个数和描述符间相对距离阈值对匹配结果的影响进行相关参数选取实验。
针对支撑区域的范围,选取同时具有旋转和尺度变换的测试图像对两种支撑区域进行实验测试,如图8所示,红色曲线表示支撑区域范围为预测框的外接圆,蓝色曲线表示预测框等比例矩形且与外接圆等面积的支撑区域。在其他参数不变的情况下圆形区域的匹配数高于矩形区域,验证了选择外接圆作为预测框的支撑区域优于矩形区域。

图8 支撑区域形状与预测框匹配数关系曲线Fig.8 Curves of matching numbers between different support areas and prediction boxes
针对最优划分梯度区间个数选取问题,梯度区间个数与正确匹配率关系曲线结果如图9所示,可以看出,在相同支撑区域中,预测框匹配数随描述符维数的增加而减小,描述符维数与匹配率之间的关系如图10所示,由拟合的实验关系可知预测框正确匹配率开始随描述符维数的增加而增加,当描述符维数达到10维时,维数增加正确匹配率保持不变。梯度方向按照每36°为一个区域划分为10个区间,即生成10维预测框描述符,相对尺度不变特征变换(Scale-invariant feature transform,SIFT)、SURF(Speeded Up Robust Features)等匹配算法降低了特征描述符的维数。
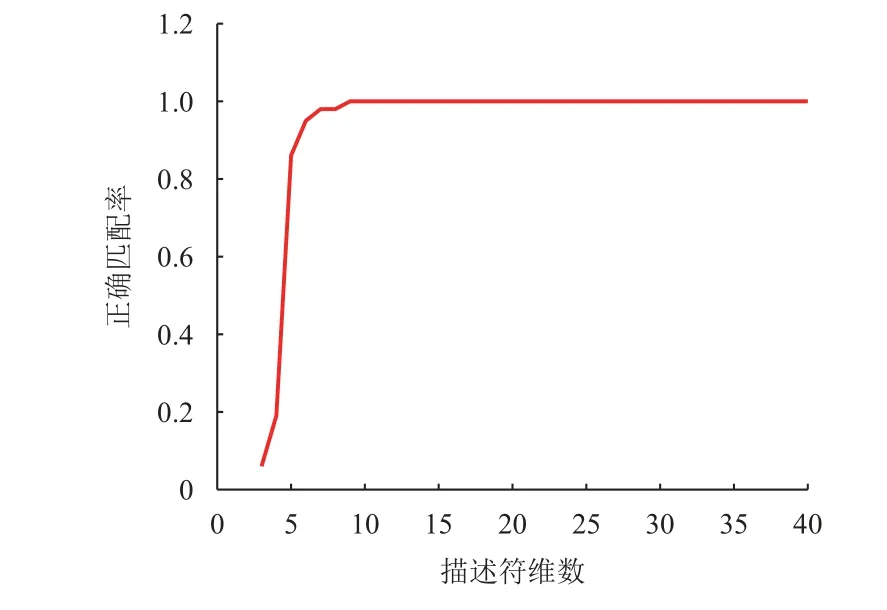
图9 梯度区间个数与正确匹配率关系曲线Fig.9 Relation curve between number of gradient intervals and the matching accuracy rate
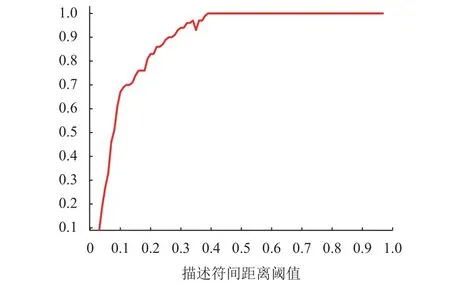
图10 不同阈值与相对匹配数之间关系曲线Fig.10 Curve of relationship between different thresholdsγ and number of matches
符间欧氏距离阈值 γ从0.01~ 0.99变化时,预测框匹配数和正确匹配率的对应关系统计曲线如图11所示。由图11可知,随着阈值γ 的提高,预测框匹配数开始增加,当参数 γ为0.1时匹配率达到最大值,随误匹配数的增加匹配率逐渐减小。因此,选择 γ为0.1作为描述符欧氏距离阈值。
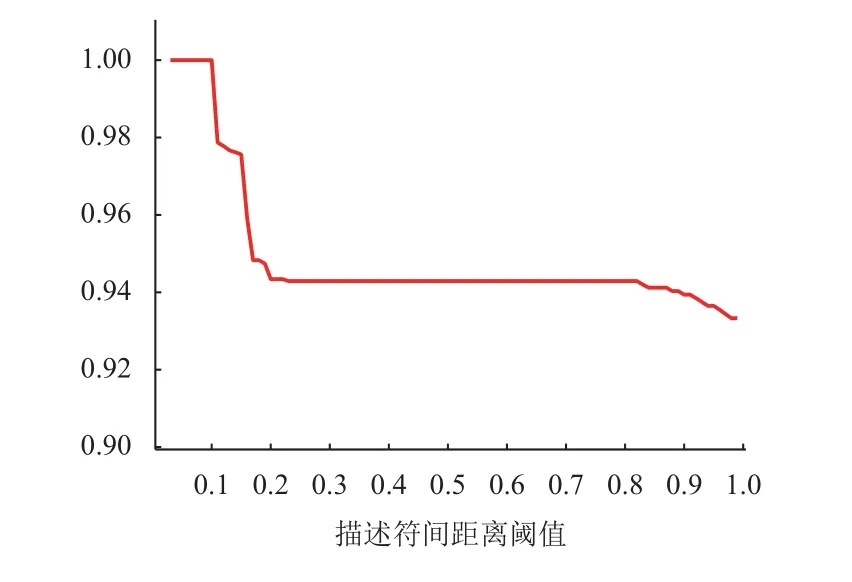
图11 不同阈值与匹配率间关系曲线Fig.11 Relationship curves between different thresholds and matching rates
3.2 实验测试
采用YOLOv4网络检测小天体陨石坑的识别结果对算法的匹配率进行验证,实验所用为美国国家航空航天局(National Aeronautics Space and Administration,NASA)官网得到的小天体Ceres(谷神星)图像[22]。实验包括尺度变换、旋转变换、亮度变化、高斯模糊及同时具有上述变换。实验结果如图12~16所示。

图12 尺度变换匹配结果Fig.12 Matching results of scale transformation

图13 旋转变换匹配结果Fig.13 Matching results of rotation transformation

图14 亮度变化匹配结果Fig.14 Matching results of brightness changes

图15 高斯模糊匹配结果Fig.15 Matching results of Gaussian fuzzy

图16 全部变换匹配结果Fig.16 Matching results of all changes
预测框匹配结果如表1所示。从表1可以看出在尺度变换、旋转变换、光照变化与高斯模糊下陨石坑匹配正确率达到90%以上。
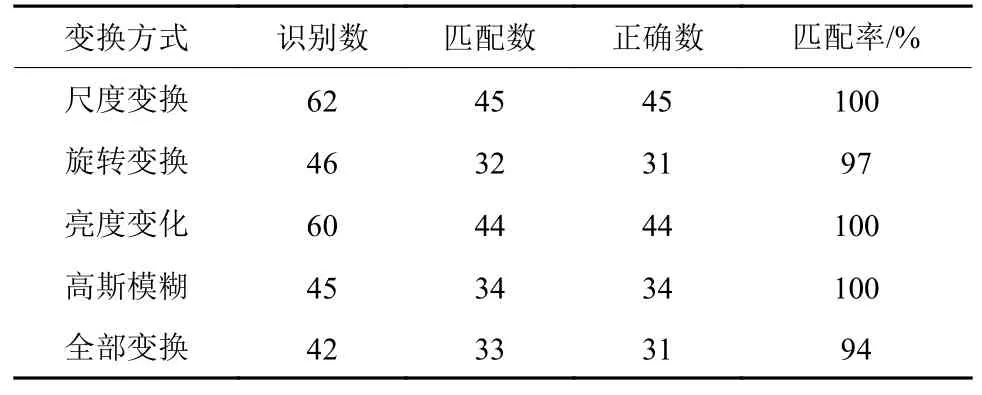
表1 预测框匹配结果Table 1 Prediction box matching results
4 结论
本文提出一种采用特征描述符实现深度学习预测框的匹配方法,主要包括导航陆标识别、预测框描述符构建、描述符匹配3部分。针对现有的以预测框为识别结果的检测网络均能实现导航陆标的匹配。通过优化支撑区域与描述符维数的选取,构建具有旋转平移、尺度、高斯模糊及光照不变性10维特征预测框描述符,与传统描述符算法相比降低了描述符维数,运算复杂度减小。后续将在保证识别结果匹配率的前提下结合误匹配剔除算法,使描述符在视角变化下具有鲁棒性。

