与地共轨小行星附近测绘轨道的性能分析与评估

石 玉，舒磊正，张 皓

（1.中国科学院 太空应用重点实验室，北京 100094；2.中国科学院 空间应用工程与技术中心，北京 100094）

引言

在小行星探测任务中，对小行星表面测绘是航天器抵近小行星后需完成的最基本且至关重要的任务，既能测量小行星形状、大小、表面地形和引力场等基本信息，又能为后续着陆、采样或撞击任务提供支持。

在小行星测绘中，对于不同的小行星探测任务，选取的测绘轨道都不尽相同。日本的“隼鸟2 号”（Hayabusa 2）探测器对小行星“龙宫”（Ryugu 162173 ）的探测选择了悬停与飞掠的测绘方案[1]，美国的“欧西里斯号”（OSIRIS-REX）探测器则选择了飞掠与绕飞的方案[2]。因此在小行星探测任务设计中，有必要对不同的轨道在小行星测绘方面的性能进行评估。

根据航天器与小行星的相对运动关系，测绘轨道主要分为悬停、飞掠和环绕3种方式，且已得到了较为充分的研究，小行星附近航天器的悬停控制研究[3-5]，小行星附近的周期轨道的计算与延拓[6-8]、小行星不规则引力场对环绕和飞掠轨道的影响等[9-12]。目前对于小行星测绘轨道的研究主要集中在动力学与控制领域，即根据小行星附近的复杂动力学环境，分析轨道的动力学特性，并在此基础上设计相应的控制器结构。而在轨道的测绘性能方面的研究非常少，即从实际的测绘任务指标出发，分析轨道的特性。

本文分析了小行星附近的动力学环境，计算了小行星附近的环绕型和飞掠型轨道，并提出了考虑小行星表面遮挡的观测覆盖模型与计算方法。论文以近球形小行星Bennu 101955和细长型小行星Eros 433为例，计算分析了其附近环绕型轨道和飞掠轨道的覆盖性、测绘时间、燃料消耗、鲁棒性等性能指标，从而衡量不同类型测绘轨道对小行星的观测效果，为未来小行星探测任务中的测绘方案规划提供支持。

1 小行星附近的动力学环境

在小行星附近，小行星的中心引力为航天器所受到的主导作用力，航天器所受到的主要摄动力为小行星非中心引力、太阳光压和太阳引力摄动。

假设小行星运行在半径1 AU的圆轨道上，其自转轴与公转轴平行，则定义如下坐标系。太阳-小行星旋转坐标系：原点在小行星质心；x轴方向沿太阳指向小行星方向；z轴沿轨道平面法向。定义小行星惯性坐标系与初始时刻的太阳-小行星重合。定义小行星本体坐标系，其中z轴沿自转轴方向，初始时刻本体系与惯性系重合。

设航天器在小行星惯性系中的位置为r，航天器运动的动力学方程可表示为

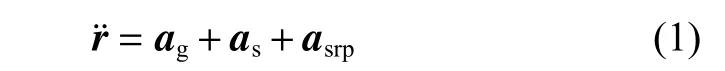
其中：ag为小行星引力；as太阳引力摄动；asrp为太阳光压。

采用球谐函数模型描述引力场，在本体坐标系中有

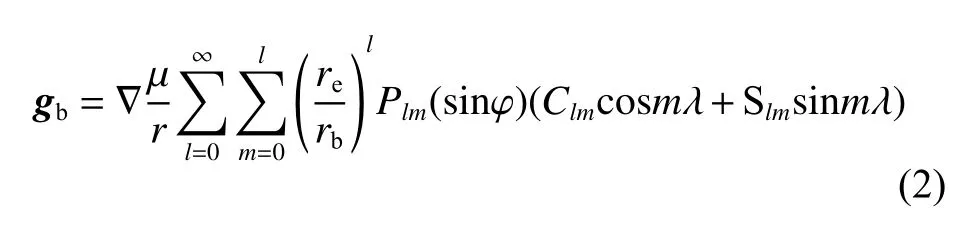
其中：µ为小行星引力常数；

re为小行星参考半径；rb、φ、λ 分别为航天器在本体系中的距离、纬度和经度，则惯性系中的小行星引力为

其中：T为本体系到惯性系的转换矩阵。

航天器所受太阳光压作用为

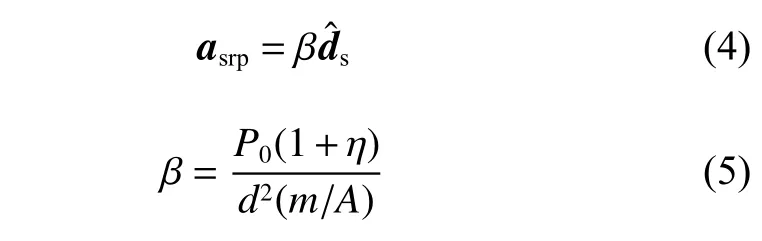
太阳引力摄动可以表示为

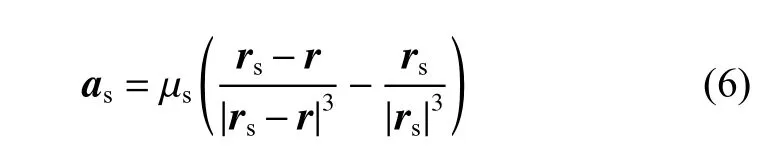
其中：µs为太阳引力常数；rs为太阳相对小行星的位置矢量。

本文选取尺寸较小，近似球形的小行星Bennu 101955和尺寸较大，细长型小行星Eros 433 的物理参数作为算例，分析小行星附近的动力学环境，其基本参数如表1所示。

表1 小行星参数信息Table 1 Physical parameters of asteroids

取航天器的反照率 η为0.4，质量与面积之比62，航天器在距离小行星不同距离下所受各个作用力的大小如图1所示，横坐标为航天器距离小行星距离与小行星平均半径的比值。可以发现，对于尺寸较小的小行星，其引力场较弱，太阳光压的影响非常明显。当航天器距离小行星Bennu约3倍平均半径时，太阳光压成为最主要的摄动力，且数量级逐渐逼近中心引力，因而分析附近轨道的动力学特性时，太阳光压是最重要的影响因素。当小行星尺寸较大时，引力场较强，此时非中心引力是最主要的摄动力，太阳光压远小于中心引力。此外，航天器在小行星附近时，所受到的太阳引力摄动非常小，其影响最弱。

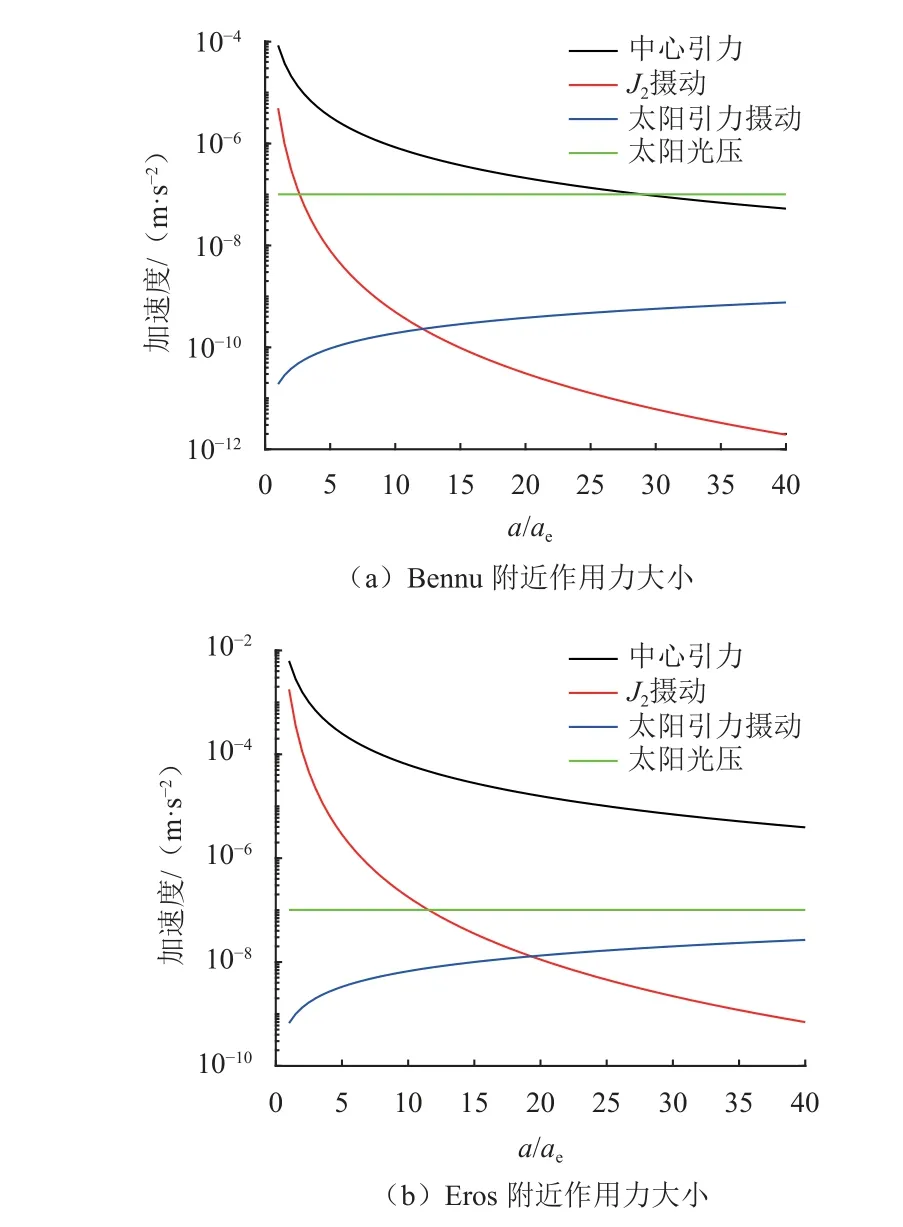
图1 小行星附近航天器所受各个作用力大小Fig.1 Magnitudes of forces of spacecraft in the vicinity of asteroids

2 小行星附近的测绘轨道

2.1 环绕型轨道

环绕型轨道是一种经典的测绘轨道，可以实现对小行星表面的周期性观测。而由于小行星附近复杂的动力学环境，环绕型轨道会受到极强的扰动，从而影响轨道的稳定性，增加撞击和逃逸的风险。因此，在设计环绕型的轨道时，一般需要考虑相对稳定的轨道作为测绘轨道。

本节采用数值方法分析小行星附近环绕型轨道的稳定性。取飞行时间为60 d，如果航天器到小行星的距离始终维持在给定的范围内，则认为该轨道适合作为小行星的环绕轨道。在数值仿真中，以Eros和Bennu为例，选取轨道的初始偏心率为0，计算不同半长轴和升交点赤经的轨道，选择轨道到小行星的距离的允许偏差范围为30%。在Bennu附近，分别计算初始距离为3、5、10倍小行星平均半径下的轨道演化情况如图2所示，其中标记颜色的区域为飞行60 d后仍处于允许距离范围内的轨道。结果表明，轨道的倾角为90°附近，升交点赤经为90°或270°附近时，轨道能够稳定飞行。其余状态下，轨道均无法实现稳定绕飞。这主要是因为Bennu附近的主要摄动力为太阳光压，绝大多数轨道在太阳光压的影响下偏心率逐渐增大，使得近星点高度逐渐降低，从而无法实现稳定绕飞。事实上，这类能够实现稳定绕飞的轨道称为晨昏线轨道[15]，其轨道平面始终近似垂直于太阳矢量方向。

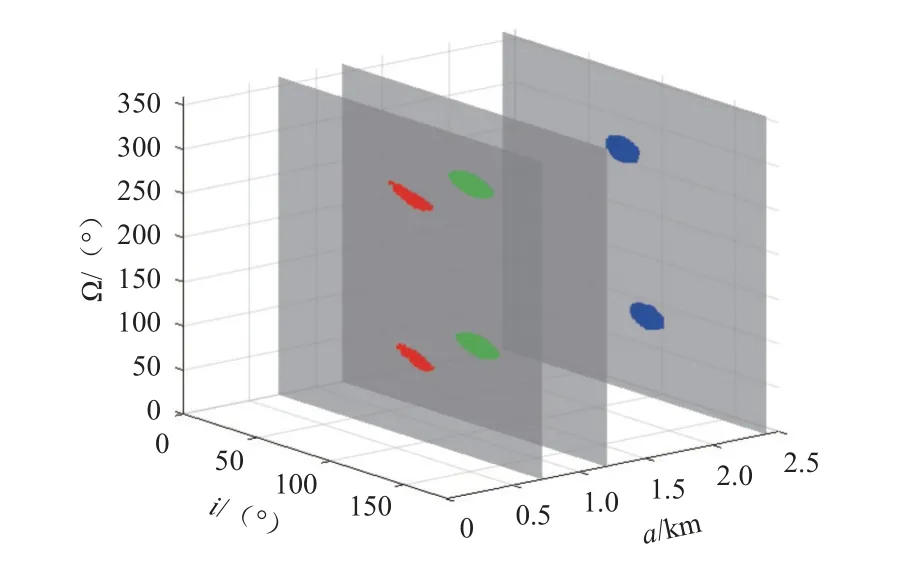
图2 Bennu附近稳定绕飞的区域Fig.2 Stable region for fly-around orbits near asteroid Bennu

Eros附近，初始距离为3、4、5倍和10倍小行星平均半径下的轨道演化情况如图3所示。其中标记颜色的区域为飞行60 d后仍处于允许距离范围内的轨道。可以看到，与Bennu不同，Eros附近的轨道演化情况与轨道半径密切相关，这主要是由于Eros附近的主要摄动力为非中心引力，其作用会随着轨道高度的增加逐渐减弱。当航天器处于3倍平均半径时，顺行轨道均不能稳定绕飞，只有大倾角的逆行轨道才能实现相对稳定的绕飞。这种现象是由C22项摄动引起的，由于C22项摄动与小行星自旋相关，从而对顺行轨道与逆行轨道有不同的影响，与已有文献结论相吻合。即小行星附近的C22项摄动会使得顺行轨道的稳定性发生变化，而对逆行轨道的影响则由于小行星的相对快速自旋而平均化，具体分析见文献[16～17]。而随着航天器距离增加，C22项摄动的影响逐渐减弱，稳定的区域逐渐增加，直到当航天器处于5倍平均半径时，绝大多数轨道均能实现稳定绕飞。这是由于航天器所受的非中心引力作用降低，轨道的稳定范围增加所致。当航天器处于10倍平均半径时，非中心引力作用继续降低，太阳光压的摄动作用逐渐明显，稳定范围减小。在特定的升交点赤经下，轨道无法实现稳定绕飞。因此，考虑到测绘轨道一般需要较大的轨道倾角增加对表面的覆盖区域，在近距离时，环绕型的轨道只适用于对低纬度地区的测绘。对高纬度地区的观测需要增加环绕轨道的高度。

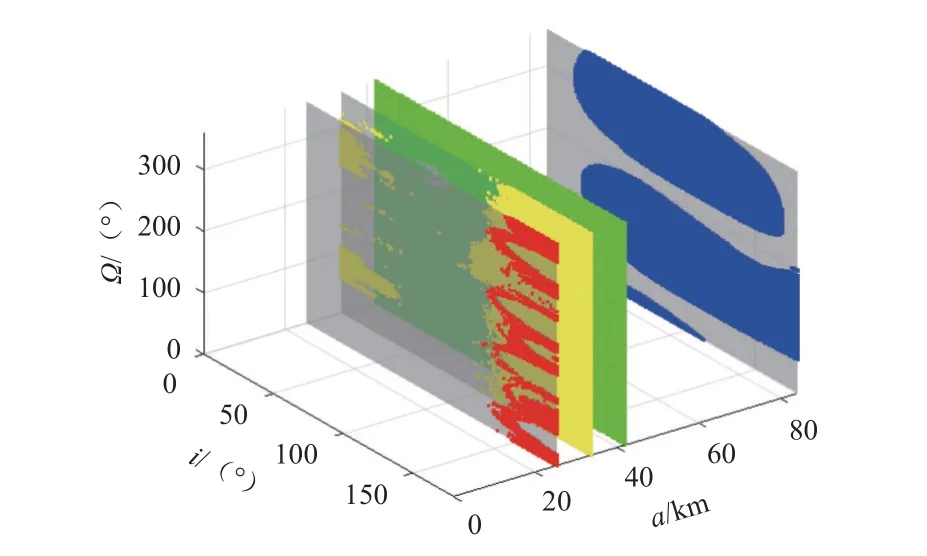
图3 Eros附近稳定绕飞的区域Fig.3 Stable region for fly-around orbits near asteroid Eros

2.2 飞掠型轨道

小行星引力场较弱，轨道机动可以显著改变飞行轨迹，因而可以通过双曲线轨道飞掠小行星的方式实现对小行星的观测。在设计飞掠型轨道时，不需要考虑轨道的长期稳定性，而更多需要关注飞掠轨道近星点附近的状态。

采用二体模型中的双曲线轨道设计飞掠轨道，其中近星点的位置由近星点的赤经和赤纬（λ，φ）和近星点距离rp描述，而近星点的速度大小由双曲线的转向角δ 确定，速度方向与当地子午面的夹角记为γ，则轨道偏心率为

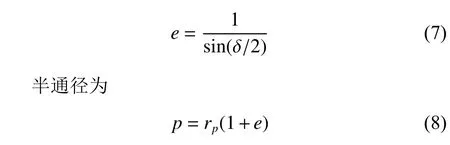
值得注意的是，轨道只有在飞掠近星点附近的较短时段内受到的非中心引力场较为显著，其余轨道段受到的非中心引力场较弱，且会随着小行星的自旋而被平均化，因而近星点时刻对轨道的影响相对较弱。

为了修正摄动力对轨道的影响，设航天器初状态的时间和位置为t0和x0，末状态的时间和位置为tf和xf，构造两点间转移的Lambert问题，即求解初始速度v0满足

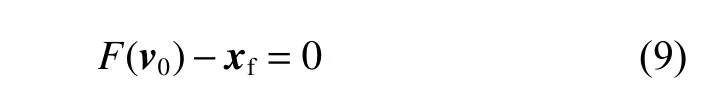
其中：F(v)为t0时刻，初始状态为[x0,v0]运动至tf时刻的位置。

以二体模型下的双曲线轨道为初始猜测，数值迭代求解方程零点，从而得到修正后的飞掠轨道。

近星点距离为5倍平均半径时，Bennu 和Eros附近从不同经度飞掠赤道面的双曲线轨道如图4所示，其中黑色轨迹为二体下的轨道，蓝色轨迹为受到扰动后的轨道，绿色轨迹为修正后的轨道。可以看到，在Bennu附近轨道飞掠轨道受到的扰动较强，使得近星点的位置产生变化，这与Bennu附近的主要摄动力是太阳光压相关，经过数值修正后，轨道可以实现对指定区域上空的飞掠。Eros附近光压影响相对较弱，因而飞掠轨道受到的影响较小。

图4 Bennu和Eros附近的飞掠轨道Fig.4 Flyby orbits around asteroid Bennu and Eros

总的来看，飞掠轨道大体沿双曲线飞行，虽然扰动会使得轨道产生偏差，但从覆盖性的角度看，由于小行星快速自旋，轨道受到的扰动对覆盖性的影响较小。

3 轨道对表面的覆盖性

3.1 观测模型

小行星表面区域的可见性取决于航天器、小行星和太阳的相对几何关系。如果太阳的入射光线照射到小行星表面，经过反射后的光线能够被航天器捕捉到，则该区域视为可见，如图5所示。对小行星表面上的区域，设其法向量为n、光线的入射角为φ、反射角为 ε、相对于航天器的视角为θ、航天器的位置为rsc，则可观测条件需满足

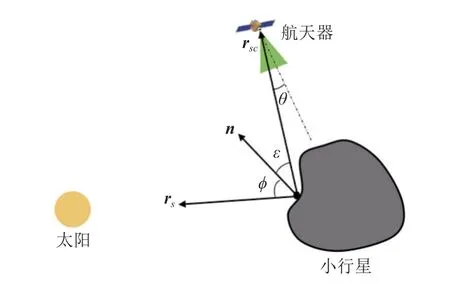
图5 小行星表面观测模型Fig.5 Observation model of the asteroid’s surface

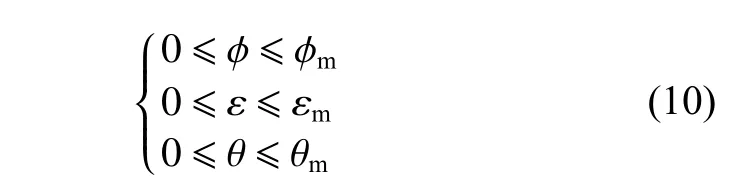
其中：φm和εm为限定的最大入射角与反射角，即当地太阳高度角和卫星高度角；θm为航天器的视场角。除此之外，航天器需要在特定的高度范围内对地面进行观测，即高度约束满足

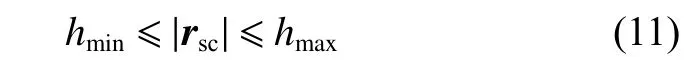
影响上述几何参数范围的最主要因素是航天器上的载荷性能，如相机的分辨率、视场角等极大的影响轨道对小行星的覆盖性。然而，这类参数的影响趋势是显而易见的。例如，增大视场角，增大允许的最大入射角和反射角，均可以极大的提高观测效果。本文主要研究测绘轨道性能分析，因而在后续的仿真计算中，不再分析这类几何参数对观测性能的影响，直接选定允许的最大入射角与反射角均为75°，允许的观测高度不超过标称高度的130%，航天器的视场角设为2.5°，且航天器始终指向小行星中心。

3.2 遮挡判断

小行星的形状不规则，表面可能存在互相遮挡的情况，还需要增加入射光线和反射光线遮挡的判据。本文采用多面体描述小行星的几何形状，其表面的每个面是三角形，如果光线同时穿过多面体上两个三角形，则距离较远的三角形被遮挡。因此，遮挡问题转化为求解空间中线段与三角形的相交问题。

设反射光线的起点为小行星表面一点P，终点为航天器Q，O为天体质心，三角形ABC（顶点逆时针排列）的法向量为nt，方向指向小行星外侧，如图6所示，为了判断三角形ABC是否会遮挡光线，首先计算三角形面法向量与光线的点积，若

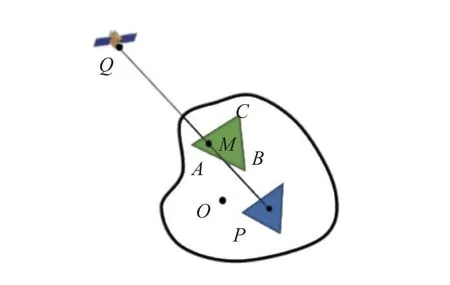
图6 小行星表面的遮挡关系Fig.6 Shading on the asteroid’s surface

则光线与三角形平行或者从三角形背面进入，不构成遮挡关系。

其次，计算光线与三角形所在平面的交点。设三角形三个顶点的坐标为（xA，yA，zA），（xB，yB，zB）和（xC，yC，zC），则三角形所在平面方程为

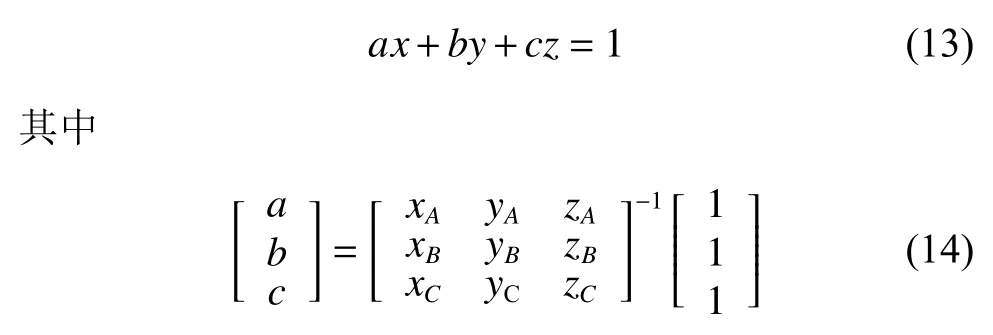
光线所在直线方程为

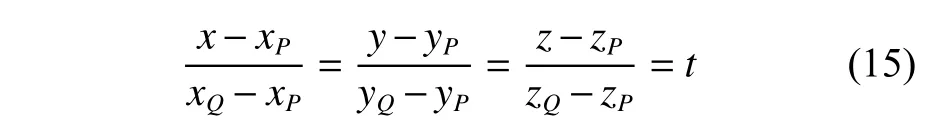
联立方程求解交点，可得

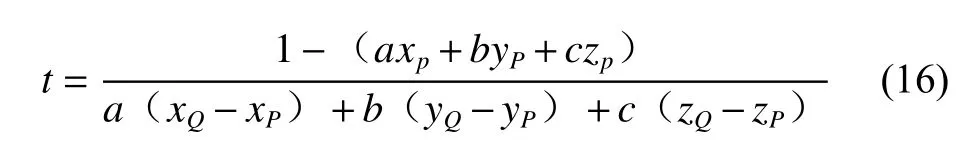
若t∉（0，1），则交点在不在线段PQ内，三角形不构成遮挡关系。

如果交点在线段上，则需要判断交点是否在三角形上，若交点M满足

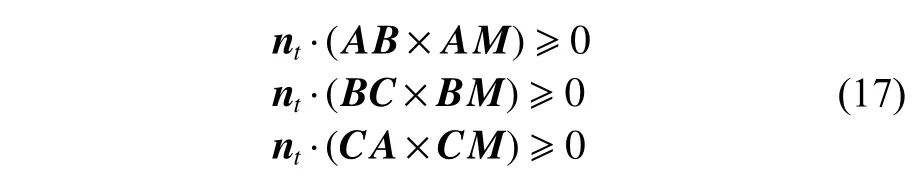
则交点在三角形ABC上。

本文在计算可见性时，以三角形形心表示该区域，如果多面体表面三角形的形心可见，则视为该三角形可见。表面覆盖率定义为已观测三角形面积的百分比。多面体表面的三角形数量众多，在计算被观测区域时，需要对其余每个三角面进行遮挡判断，会极大地增加计算量。因此可以根据小行星的多面体模型，计算得到多面体每个三角形所在地平线以上的其余三角形，并预先存储。在计算时，只需计算对应地平线上的三角形的遮挡关系即可。小行星表面遮挡指定三角形的区域如图7所示，其中绿色区域为蓝色三角形当地地平线以上，且仰角高于某一最小仰角（本文取15°）的部分，对蓝色三角形的观测构成潜在的遮挡关系。Eros表面所有可能被遮挡的三角形如图8所示，可以看到，Eros表面可能被遮挡的区域主要集中在小行星中部凹陷处，对相应的观测带来更多约束。

图7 小行星表面遮挡指定三角形的区域Fig.7 Regions of the asteroid’s surface blocking the selected triangle

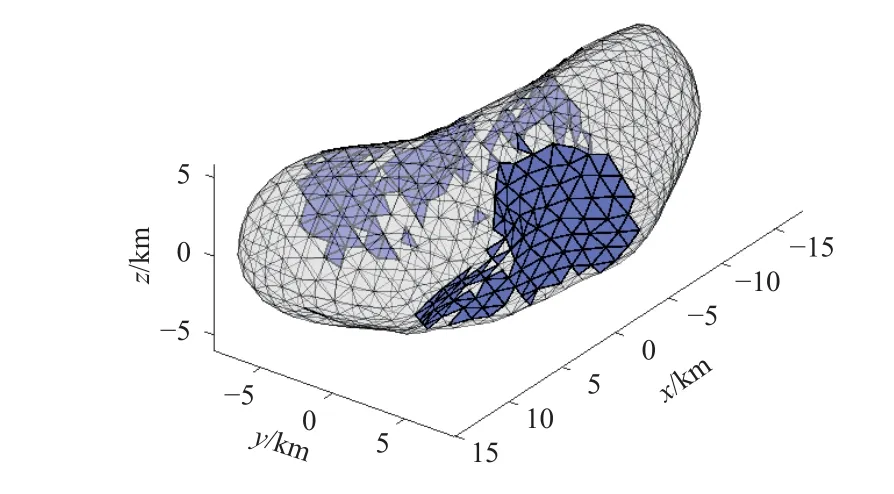
图8 小行星可能被遮挡的三角形区域Fig.8 Triangles that may be blocked by the asteroid’s surface

4 测绘轨道性能分析

4.1 覆盖性

对于环绕轨道而言，为提高覆盖率，通常会选择高轨道倾角的环绕型轨道，以实现对小行星高纬度地区的覆盖，因此，根据第2节计算得到的环绕型轨道，选定环绕型轨道的倾角为90°，轨道半径为5倍平均半径，计算不同升交点赤经的轨道在一个轨道周期内对小行星表面的覆盖率，其中观测模型的参数在第3节给出，计算结果如图9所示。结果表明，对Bennu而言，由于太阳在180°方向附近，因此当升交点赤经在180°附近时，覆盖率最高，在90°和270°时，覆盖率较低。注意到覆盖率随升交点赤经的变化曲线并非严格对称，这主要是因为轨道受到的扰动非常大，从而改变的轨道的高度，影响了覆盖率。Eros附近环绕轨道的覆盖率受升交点赤经的影响不大，可见Eros的不规则形状极大地影响了轨道对表面的覆盖率。

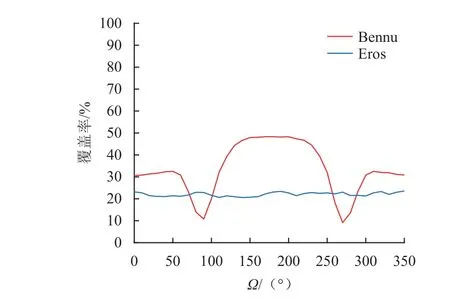
图9 环绕型轨道一个轨道周期的覆盖率Fig.9 Coverage rate of fly-around orbits in 1 revolution

对飞掠型轨道而言，由于经度的影响在环绕型轨道中已经体现，这里讨论近星点纬度和飞掠方向对覆盖性的影响。取近星点距离为5倍平均半径，转向角为60°，纬度分别取南北纬80°，南北纬40°和0°，近星点速度与当地子午面的夹角为0°～360°，计算轨道的覆盖率，结果如图10所示。可以发现，Eros的不规则形状导致其覆盖率低于Bennu。随着纬度的升高，覆盖率显著下降。这是因为赤道面地区的面积大，光照条件好，所以覆盖率高。对于单次飞掠而言，覆盖率最大的方式为从赤道附近，以较低的轨道倾角，逆着小行星的自旋方向的飞掠轨道，其覆盖的面积如图11所示。

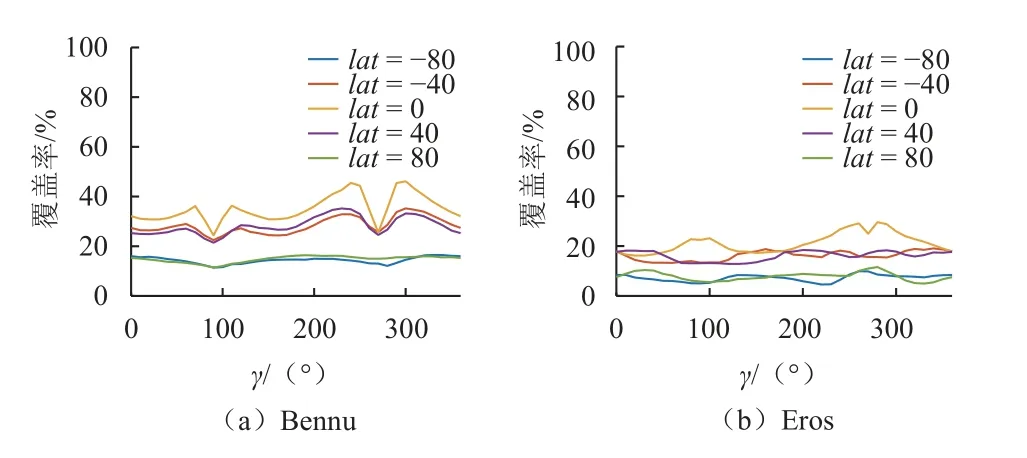
图10 Bennu与Eros附近飞掠型轨道的覆盖率Fig.10 Coverage rate of flyby orbits near Bennu and Eros

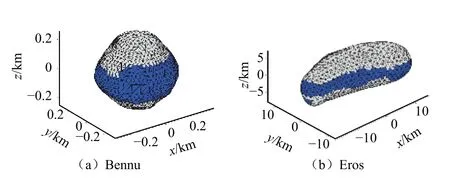
图11 Bennu与Eros附近飞掠型轨道的覆盖区域Fig.11 Covered region of flyby orbits near Bennu and Eros

4.2 时间与燃料特性

无论是环绕轨道还是飞掠轨道，无法通过短时间绕飞或单次飞掠实现对小行星表面绝大多数地区的覆盖，因而需要讨论轨道实现大范围覆盖所需的时间。对于环绕型轨道而言，长时间的环绕需要选择稳定的环绕轨道，根据第2节对轨道稳定性的分析结果，选择Bennu附近的初始倾角90°、升交点赤经80°的轨道，以及Eros附近初始倾角90°、升交点赤经180°的轨道，计算轨道飞行20 d的覆盖性曲线，如图12所示。其中Bennu附近的环绕轨道在20 d内能达到90%以上的覆盖率，并趋于稳定，Eros附近的环绕型轨道在10 d内达到80%以上的覆盖率并趋于稳定。Eros附近的环绕轨道的光照条件明暗交替，其覆盖曲线呈现明显的阶跃特征，而Bennu附近的环绕轨道位于晨昏线附近，阶跃特征不明显，但随着摄动作用的影响，轨道面产生小扰动，阶跃特征逐渐呈现。此外，由于环绕型轨道可以实现较长时间的稳定绕飞，在理想情况下环绕型轨道在测绘过程中燃料消耗为0。

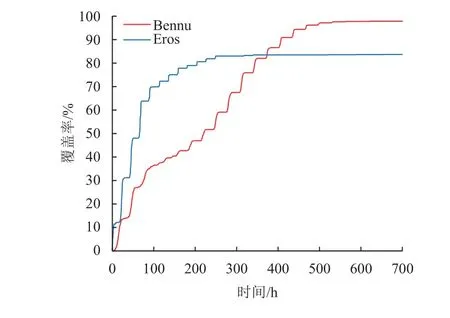
图12 30天环绕轨道时间-覆盖率曲线Fig.12 Time-coverage curve of fly-around orbits for 30 days

对于飞掠轨道而言，一般需要在飞掠过程中施加机动脉冲将多个单次飞掠轨道拼接成多次飞掠轨道，从而提高覆盖率。本文考虑南北向和东西向的两种飞掠方式，近星点距离为5倍平均半径，最远点距离为15倍平均半径，轨道转向角60°，其中南北向轨道的沿赤经为180°的双曲线轨道多次往返飞掠，东西向轨道的近星点纬度从南纬90°到北纬90°均匀分布，结果如图13所示。

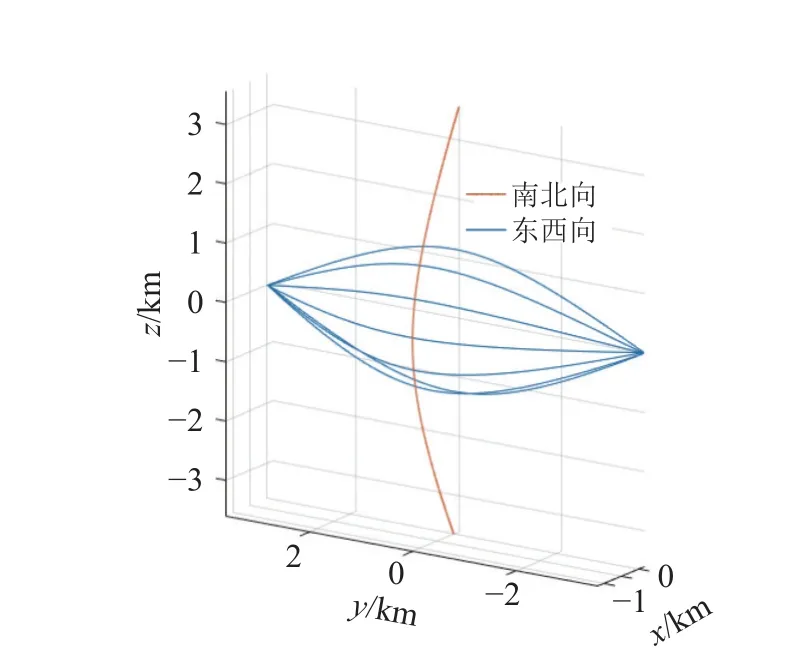
图13 飞掠轨道的两种方式Fig.13 Two types of flyby orbits

Bennu和Eros附近飞掠轨道的时间、覆盖率和燃料消耗（Δv）随飞掠次数变化的统计结果如表2所示。可以看到，随着飞掠次数的增加，两种飞掠方式的时间，燃料消耗和覆盖率均增加。与环绕轨道相比，两种飞掠方式的轨道均能通过提高飞掠次数达到与环绕轨道相当的覆盖率，并且所需时间减少了一半以上。然而在燃料消耗方面，Bennu附近飞掠轨道的消耗远小于Eros附近的轨道，这主要是由于Bennu的引力场较弱，轨道机动作用更明显。因此，对于本文所考虑的测绘问题，多次飞掠模式不适合作为引力场较强的小行星探测任务中的测绘轨道。

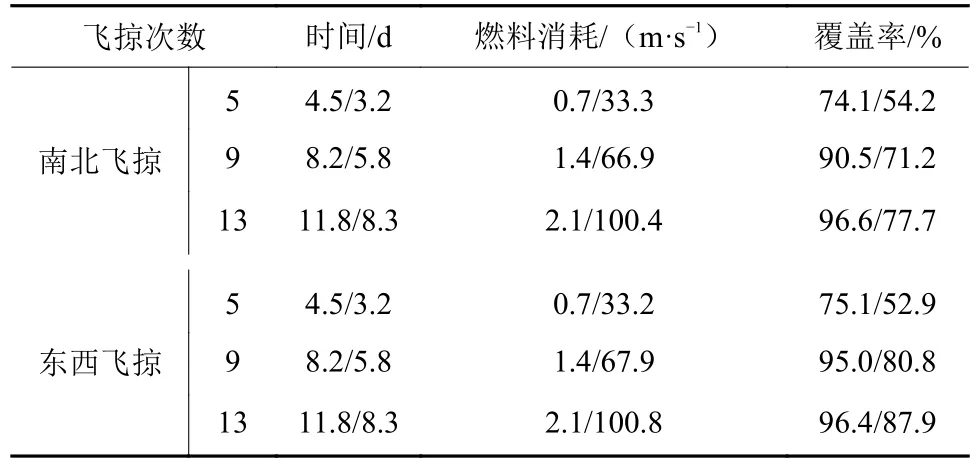
表2 Bennu/Eros附近飞掠轨道的时间、燃料和覆盖率Table 2 Time，fuel cost and coverage rate for flyby orbits near Bennu/Eros

4.3 鲁棒性

由于各种扰动的存在，航天器总会偏离预定的轨道。本节考虑模型误差对测绘轨道的影响（主要由小行星的引力场数的不确定性引起），即讨论当小行星所受到的作用力存在误差的情况下，设计的环绕与飞掠型轨道是否能够实现目标。这里将航天器所受的实际作用力按比例增大和缩小，分析轨道对于模型误差的鲁棒性。

取4.2节的环绕轨道为例，仿真时间为30 d，其最近点距离、最远点距离和覆盖率如表3所示。结果表明，在10%的模型误差范围内，Bennu和Eros的模型误差对环绕轨道的影响在允许范围内，当误差达到15%时，Eros附近的环绕轨道无法保持稳定。在覆盖性方面，模型误差对覆盖性的影响相对较小，且随着航天器所受作用力的增大，覆盖率逐渐降低。

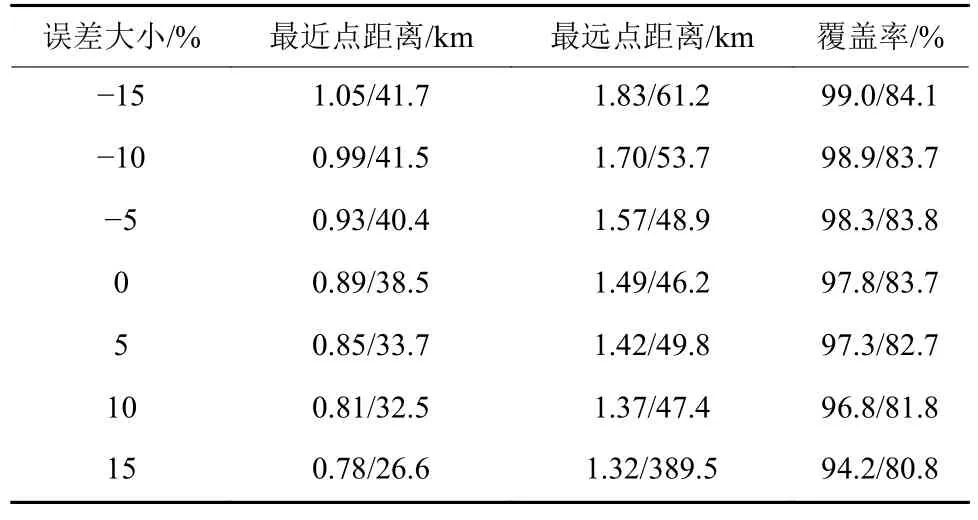
表3 Bennu/Eros附近环绕轨道的鲁棒性Table 3 Robustness of fly-around orbits near Bennu/Eros

对于飞掠轨道而言，选取4.2节中的南北向飞掠轨道，仿真结果如表4所示。结果表明模型误差对飞掠轨道的影响相对较小，可以看到，在15%的误差范围内，Bennu和Eros附近的飞掠轨道依然能够完成预定的观测，其近星点的距离和覆盖率的变化相对较小。随着航天器所受作用力增大，近星点高度降低，相应的覆盖面积减小。因此飞掠型的轨道相比于环绕型轨道更适合模型不确定性较大的小行星。

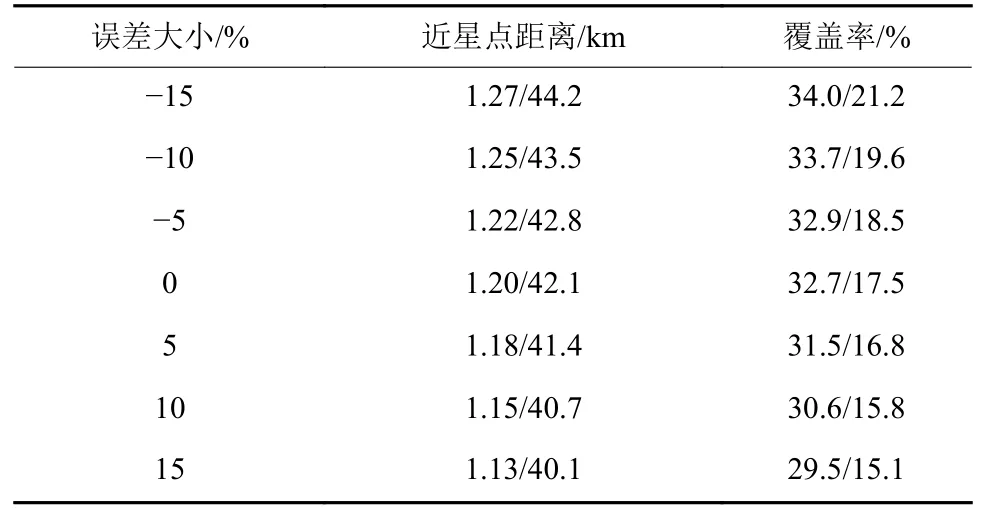
表4 Bennu/Eros附近飞掠轨道的鲁棒性Table 4 Robustness of flyby orbits around Bennu/Eros

5 结论

本文针对小行星任务中的探测侦察问题，分析比较了小行星附近的环绕型与飞掠型测绘轨道的特性。总的来看，环绕型轨道和飞掠型轨道均能实现对小行星的测绘。具体而言，环绕型轨道一般观测周期较长，燃料消耗低，但强烈依赖小行星附近的动力学环境，对于引力场较弱的小行星，多数环绕型轨道无法实现稳定绕飞。飞掠型轨道能够快速实现对小行星的观测，且对小行星的模型不确定具有较强的鲁棒性，但是需要消耗燃料进行机动实现对目标的多次飞掠，因而对于引力场较强的小行星，其燃料消耗较大。本文以近球形小行星Bennu 101955 和细长型小行星Eros 433为例，考虑小行星附近的复杂动力学环境与小行星不规则形状的相互遮挡关系，计算了环绕型轨道和飞掠型轨道的稳定性、覆盖率、测绘时间、燃料消耗以及鲁棒性等指标，并分析了环绕型轨道和飞掠型轨道的测绘特性与适用范围，为未来小行星探测任务中的测绘方案规划提供支持。