双小行星系统不规则引力场中的共振轨道动力学研究

崔书豪，王 悦，张瑞康

（1.北京航空航天大学 宇航学院，北京 102206；2.北京空间飞行器总体设计部，北京 100094）

引言

自1993年“伽利略号”（Galileo）探测器发现首个双小行星系统——Ida 243及其卫星Dactyl，越来越多的双小行星系统相继被发现，引起了广泛的关注。根据观测数据估计，双小行星系统约占近地小行星（Near Earth Asteroids，NEAs）总数的16%左右[1]。双星系统独特的形成机制有助于更好地研究小行星的演化过程；一次探测两颗小行星，可降低发射成本、丰富任务成果。因而近年来双小行星系统逐渐成为小行星探测任务的热点目标。

2021年10月美国发射的“露西号”（Lucy）探测器[2],将在未来12年中飞掠探测多个特洛伊族小行星，其中就包括Eurybates 3548和Patroclus 617 两个双小行星系统；2021年11月，美国国家航空航天局（National Aeronautics and Space Administration，NASA）发射的“双小行星重定向测试”（Double Asteroid Redirection Test，DART）[3]将访问近地双小行星系统Didymos 65803，通过动能撞击器改变小行星轨道，进而验证近地小行星的防御技术；另外，NASA的小型创新行星探测（SIMPLEx）项目还通过了“杰纳斯”（Janus）任务[4]，将以近地双小行星系统FG3 1996和VH 1991 为目标，采用2个轻质量、低成本的小型航天器对其进行高分辨率成像与高精度建模，分析双星系统的形成与演化。

在双小行星系统的探测任务中，选择合适的环绕探测轨道尤为关键。研究表明[5]，共振轨道不仅可作为长期驻留轨道，对目标进行长时间稳定的观测与成像，有些还可作为中间过渡轨道，可大幅降低轨道转移过程中燃料的消耗。现有的探测任务中，“星际边界探测器”（Interstellar Boundary EXplorer，IBEX）[6]和“凌日系外行星巡天卫星”（Transiting Exoplanet Survey Satellite，TESS）[7]分别运行在地月系统稳定的3∶1和2∶1共振轨道上，为实施任务提供了长期稳定的观测条件；欧洲航天局（European Space Agency，ESA）的“木星冰月探测者”（JUpiter ICy moons Explorer，JUICE）[8]也设计选用共振轨道作为木星系的探测轨道之一，实现对木卫二（Europa）的近距离飞掠。尽管目前共振轨道的应用主要集中在地月系统和木星系统等，但其轨道特性也能很好地满足双小行星系统探测任务的需要，因而具有重要的潜在应用价值。

轨道动力学研究依赖于适合的力学模型。然而由于小行星自身体积质量较小，几何形状不规则，简单的质点引力模型无法准确刻画小行星的弱引力场。早期学者们利用某些简单几何体近似小行星的不规则引力场，其中包括细直棒[9]、圆环[10]、立方体[11]、哑铃体[12]等等，这种方法便于理论分析与计算，但过于理想化，与实际情况存在一定的偏差；球谐函数法[13]利用Legendre级数在原有质点基础上进行摄动处理，理论上可以展开到无穷项，实际应用时可根据精度需要作任意阶截断；质点群法[14]是另一种较为直观的描述小行星引力场的方法，通过将小行星离散为若干体积单元，用所有体积单元引力场的叠加来近似小行星完整的引力场；Werner[15]于1994年提出的多面体法用上千个点与面对不规则小行星进行几何建模与物理仿真，完整包含了小行星的重要表面特征，该方法基于均匀质量分布假设，可相对精确地刻画出小行星不规则引力场；后续学者们又提出应用有限元方法[16]和虚拟边界法[17]等来处理非均匀质量分布的问题，使引力场模型更加逼近真实天体。

关于双小行星系统中共振轨道的研究，Chapped和Howell[18]在圆型限制性三体问题（Circular Restricted Three-Body Problem，CRTBP）的基础上，提出用球-椭球模型和双椭球模型刻画双星系统的引力场，计算了多组平面与三维共振轨道，并借助流形实现了共振轨道与其它类型轨道之间的相互转移。Damme等[19]利用球-椭球模型研究了近地双小行星系统 GT 1996 和FG3 1996 共振轨道的轨道寿命，发现太阳光压是影响共振轨道寿命的重要因素之一。Yang等[20]基于双椭球模型对双小行星系统Isberga 939 的共振轨道进行设计与分析，总结了不同共振比的共振轨道族的轨道特性，还针对各类微小摄动提出了一种全局收敛的滑模控制方法。对于接触式双小行星系统，Feng等[21]建立了相互接触的球-椭球模型来刻画其高度非球形引力场，经过仿真计算发现，中心天体的不同角速度会影响共振轨道在某些共振比下的存在性。然而，目前双小行星系统周围的共振轨道研究中采用的引力场模型还比较简单，球-椭球模型或双椭球模型并不能刻画小行星引力场的不规则性。

本文将采用一种多面体-椭球模型来描述双小行星系统的引力场[22]，基于双同步假设建立双星系统附近的轨道动力学方程，相对已有研究提高了计算精度；随后采用打靶法计算求解不规则引力场中的共振轨道，通过参数延拓得到不同共振比的轨道族；进而分析共振轨道族的稳定性与分岔特点，并借助庞加莱截面基于共振轨道流形设计了同宿转移轨道，对于未来的双小行星探测任务特别是强不规则小行星的探测轨道设计具有一定的参考意义。

1 动力学建模

1.1 多面体-椭球引力模型

考虑到主星的体积和质量较大，其不规则引力场影响较为显著，而从星体积和质量相对较小，且形状模型的精度没有主星高，因此采用多面体-椭球模型刻画双小行星系统的引力场。假定主从星以角速度 ω绕其公共质心进行圆轨道运动，由此建立系统的质心旋转坐标系O-xyz如图1所示，其中x轴正方向为主星指向从星的方向，z轴方向与角速度矢量方向平行，y轴满足右手定则。基于双同步假设，即主从星自旋同步，从星自旋周期与轨道周期同步，系统为自治系统，主从星的位置始终固定在旋转坐标系的x轴上。主星到从星的位置矢量为d，坐标原点到空间某一点的位置矢量为r，主星与从星的质量分别为m1、m2，定义参数µ 为系统引力系数

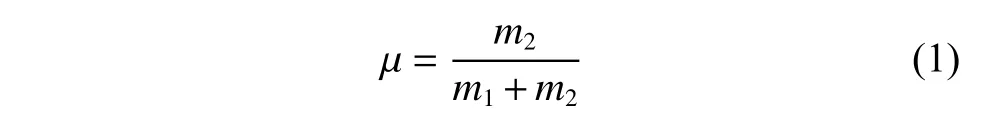
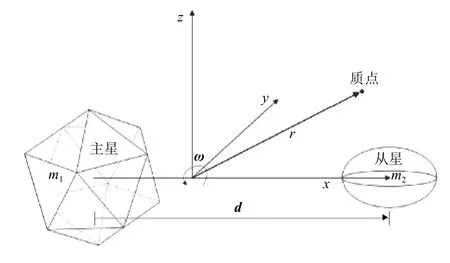
图1 双小行星质心旋转坐标系Fig.1 The rotating frame in the binary asteroid system

在此模型下，双星系统附近空间质点运动的动力学方程为

其中：Upoly与Uell分别表示主星与从星在空间中某一点的引力势。

主星采用多面体模型，多面体模型的引力势[23]可以表示为

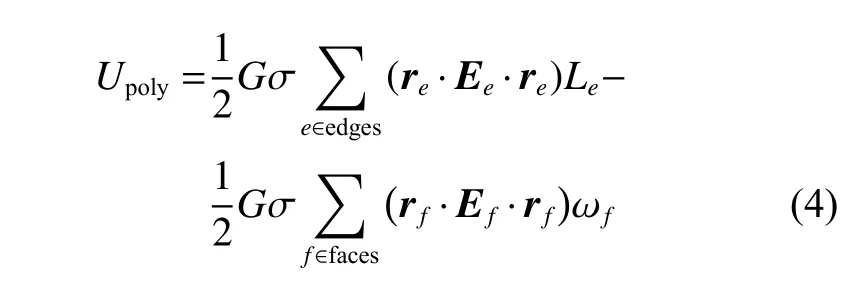
其中：σ为匀质多面体的密度；re和rf为空间任意点到多面体某楞和面上任意点的位置矢量；Ee和Ef为描述楞与面物理属性的张量矩阵。

从星采用椭球模型，椭球模型的引力势[24]可以表示为

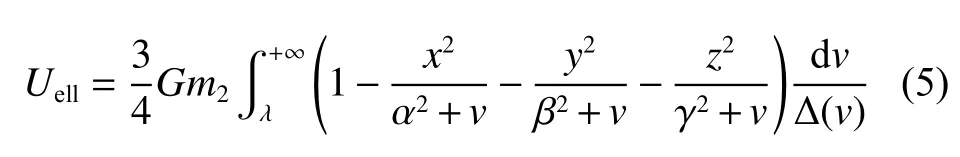
其中：α、β、γ 为椭球的3个半轴长度，0 ≤γ ≤β ≤α，参数 λ及 Δ(ν)满足下述关系

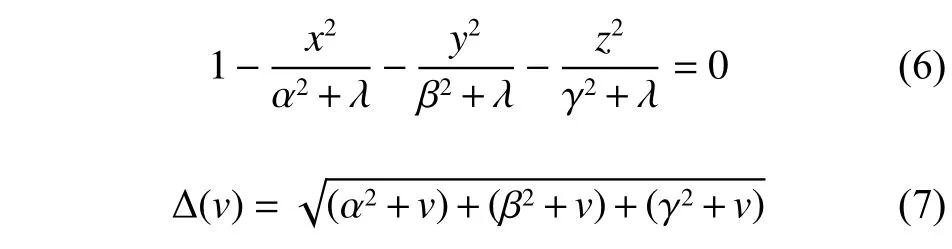
1.2 动力学环境初步分析

本文选取双小行星系统Moshup 66391 作为研究对象，其基本参数如表1所示[25-26]。

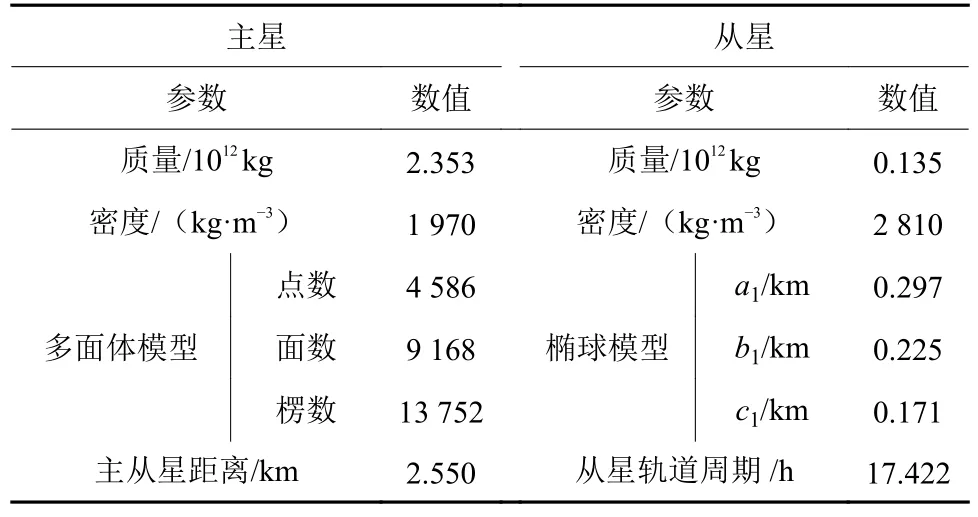
表1 66 391 Moshup双星系统参数Table 1 Parameters of the 66 391 Moshup system

应用1.1节的动力学模型，轨道运动的动能与势能分别为

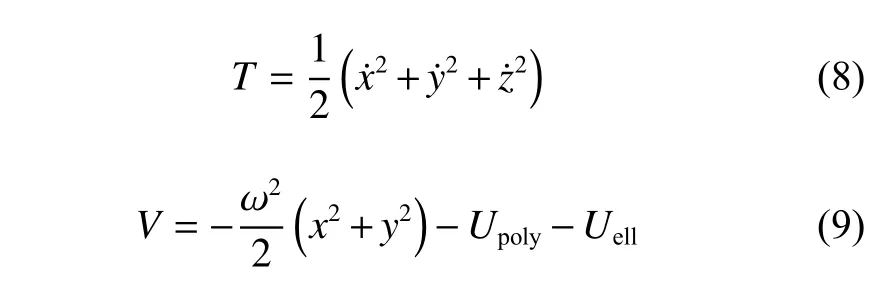
平动点是相对于旋转坐标系保持静止的点，即相对速度为零，相对位置保持不变，等效势能一阶导数为零，即

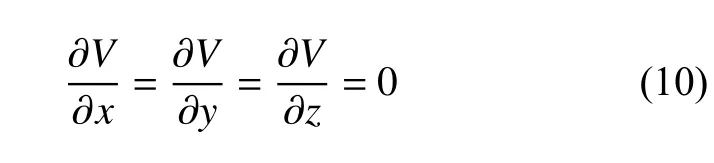
平动点是三体问题的特殊解，对研究系统动力学环境和进一步的轨道设计具有重要作用。双小行星系统Moshup 66391 的5个平动点如图2所示，具体位置数据如表2所示。可以发现在多面体-椭球模型下，平动点的主要特征基本保留了圆型限制性三体问题的平动点；但由于多面体模型的不对称性，3个共线平动点在x轴附近存在一定偏差，2个三角平动点也不再严格位于等边三角形的顶点处，同时所有平动点在z方向也存在小幅偏移。

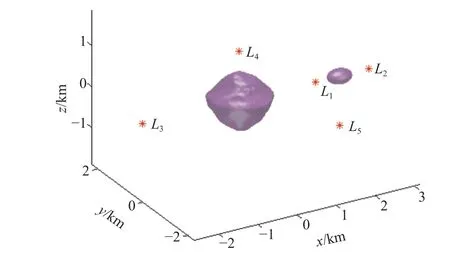
图2 66 391 Moshup 双星系统的5个平动点Fig.2 The five libration points in the 66 391 Moshup system

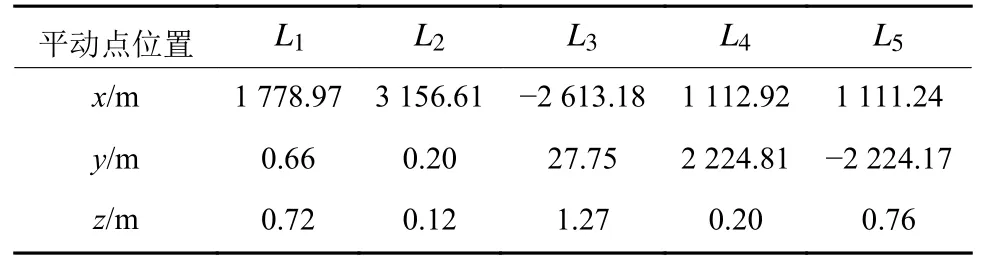
表2 5个平动点的位置数据Table 2 Locations of the five libration points

三体问题存在能量守恒关系，即动能与势能之和在不受系统外力的影响下保持不变。

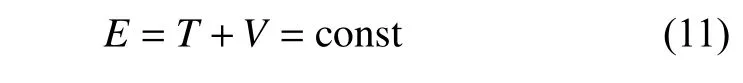
通常定义-2E为Jacobi常数，用C表示。

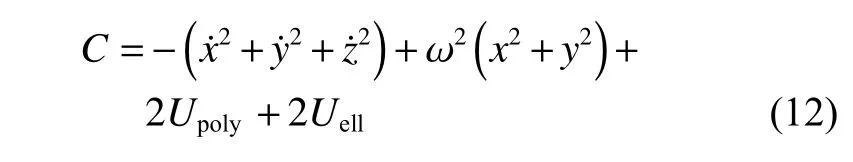
根据5个平动点的坐标得到对应的Jacobi常数如表3所示。对比圆型限制性三体问题，第4和第5个平动点的Jacobi常数不再完全相等，而是存在微小的差别。

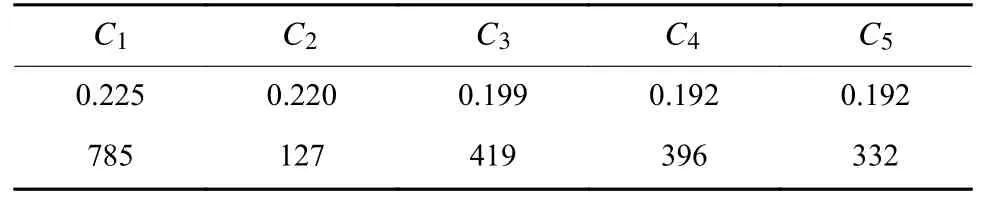
表3 5个平动点的Jacobi常数Table 3 Jacobi constant of the five libration points单位：J

当给定Jacobi常数时，令速度为零，系统的所有能量均视为势能，这样的空间集合所构成的曲面被称为零速度曲面。在曲面空间内任意点出发，到达曲面时的速度为零，运动无法穿过曲面，因而零速度曲面是空间可行区域与不可行区域的分界面，可行运动区域又称为Hill域。将零速度曲面投影到旋转坐标系的x-y平面、x-z平面、y-z平面，得到零速度曲线。根据前面计算的平动点Jacobi常数，绘制不规则引力场模型中的零速度曲线，如图3所示。

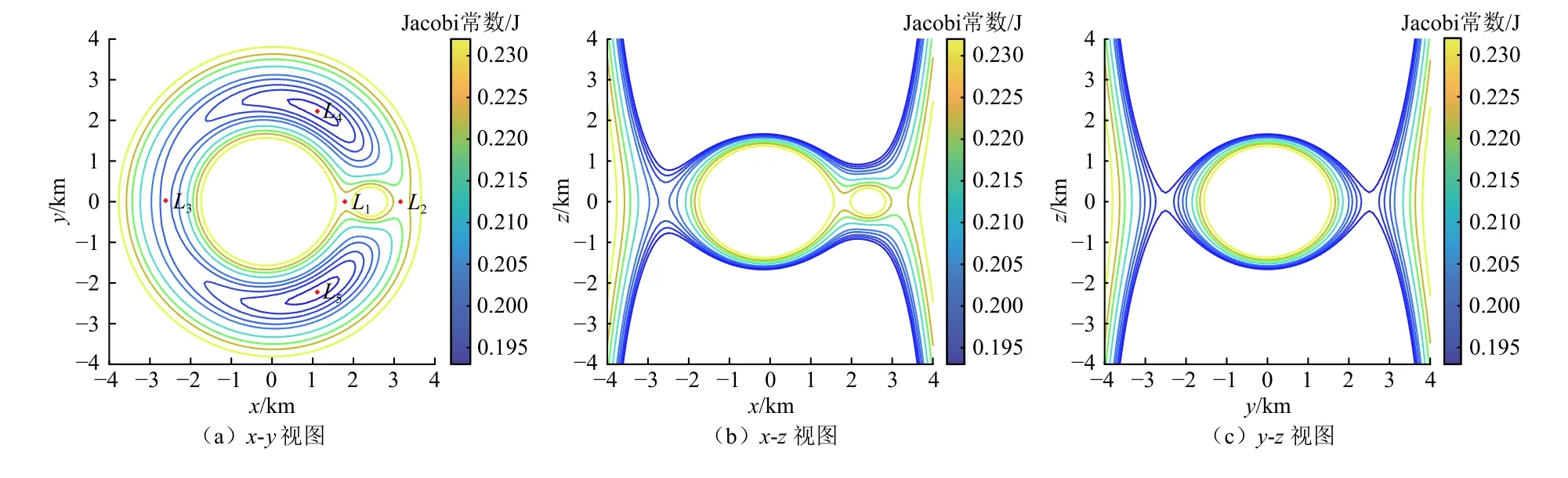
图3 66 391 Moshup 系统的零速度曲线Fig.3 Zero velocity curve of the 66 391 Moshup system

通过对双小行星系统的动力学环境初步分析，可以得到如下结论：引入不规则多面体-椭球引力场模型，使三体问题不再具有良好的对称性，在更加接近实际情况的同时，也大幅增大了系统附近轨道运动的复杂性；引力场的不规则是双小行星系统在轨道设计阶段需要考虑的重要因素之一。

2 共振轨道设计

在主星、从星和探测器构成的三体问题中，共振轨道被定义为探测器的轨道周期与从星的轨道周期呈简单整数倍关系，即p:q共振是指从星绕主星运行q圈时探测器在大致的时间内绕主星运行p圈。

由第1节对动力学模型的计算，发现引力场具有一定的不对称性，这给共振轨道的设计带来了一定的困难。现有求解共振轨道的方法主要针对引力场对称的模型，将二体问题的解作为初值进行打靶得到圆型限制性三体问题中的共振轨道。在此基础上，采用同伦法将共振轨道从三体问题延拓到不规则引力场的双星系统中，可获得一系列不同共振比的共振轨道；随后使用单参数连续法对单条轨道进行延拓，进而得到完整的共振轨道族。

2.1 共振轨道的计算

首先忽略双小行星系统的形状与次星的质量，考虑最简单的二体模型。结合轨道根数与轨道位置速度的转换和共振轨道对于轨道周期的限定条件，可以求得共振轨道在二体模型下的初值[5]。

获得轨道初值后，就可以通过打靶法求解圆型限制性三体问题中的共振轨道。打靶法，即利用微分修正的思想，不断调整控制变量的初值以达到预期的约束条件。对于共振轨道问题，控制变量为轨道初始时刻的位置与速度，即

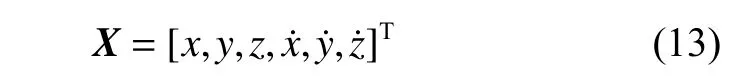
控制变量满足圆型限制性三体问题的动力学方程

约束条件为周期轨道满足初末状态的连续性，即约束方程为

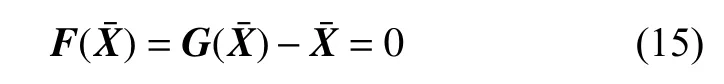
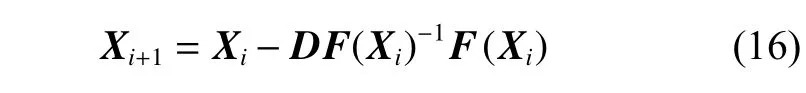
随后，采用同伦法将三体问题中的共振轨道缓慢延拓至双星系统中。同伦法的优势在于将简单问题与复杂问题建立联系，由已知的简单情况逐渐过渡到不方便求解的复杂情况中。构造基于同伦法的动力学方程

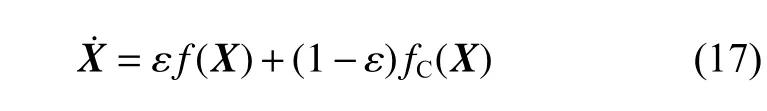
其中：f(X)表示不规则双星引力场的动力学方程右端项；fC(X)表示圆型限制性三体问题的动力学方程的右端项；ε为同伦参数。当ε=0时，系统为圆型限制性三体问题；将前面求解的三体问题共振轨道初值代入并缓慢增大ε 的取值，依次利用打靶法求解不同ε 值对应的共振轨道；当ε=1时，系统变为具有不规则引力场的双星系统，相应的共振轨道也随之获得。三体模型和多面体-椭球模型中的共振轨道如图4所示。

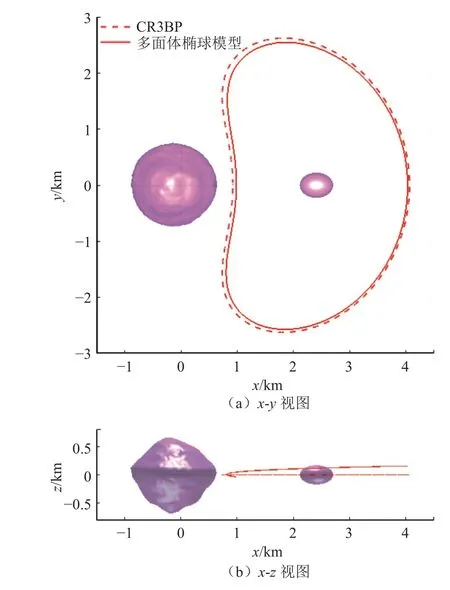
图4 不同引力模型中的共振轨道图Fig.4 The resonant orbits in different gravity models

2.2 共振轨道族的延拓

单条共振轨道往往无法体现出轨道的完整特性，通过轨道的延拓可以获得结构相似、性质接近的整族轨道，既可以把握相同共振比轨道的整体特性，分析特定参数改变对于轨道演化的影响，同时对比轨道族之间的动力学规律，又可以为探测任务提供更为丰富的轨道选择。

针对不规则引力场中的轨道，这里使用单参数连续法对轨道进行延拓。选取轨道的某一个物理参数，如轨道周期、轨道能量、轨道初值中的某一个状态量等，施加一个微小的扰动重新进行打靶，并沿着这一参数增大或减小的方向连续延拓，就可以得到一组结构相似的共振轨道族。4种不同共振比的轨道沿轨道周期延拓得到的共振轨道族如图5所示，具体的轨道初始状态如表4所示。

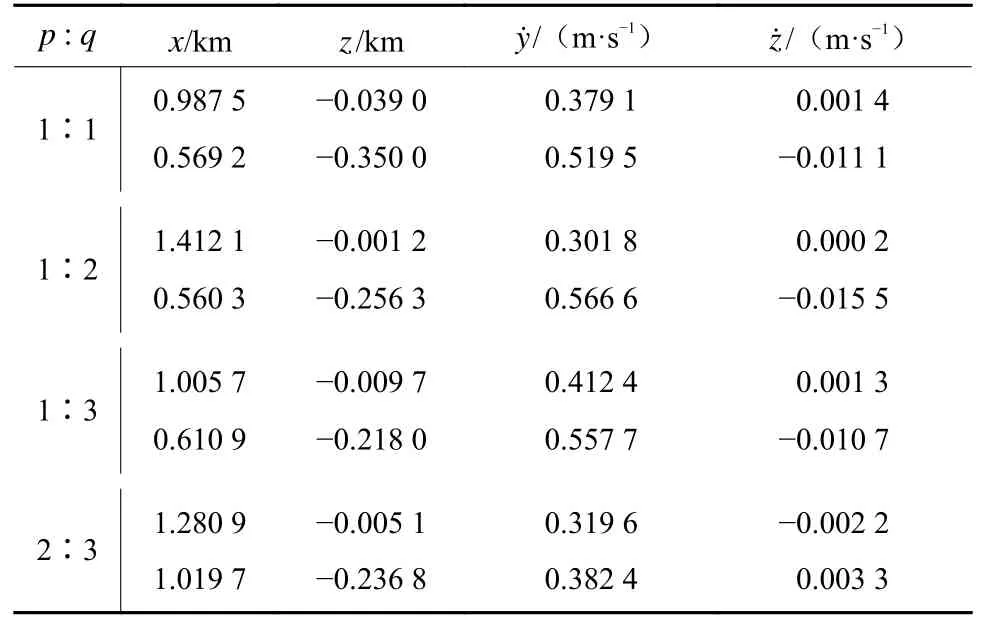
表4 共振轨道族的初始状态Table 4 Initial state of the resonant orbit families

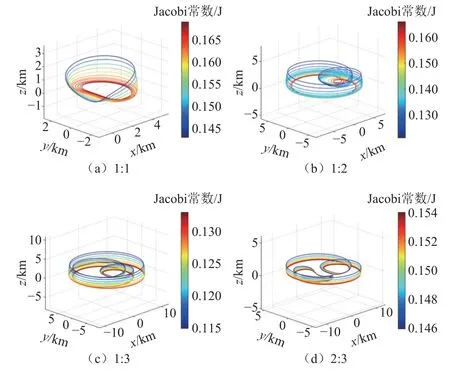
图5 66 391 Moshup 系统的若干共振轨道族Fig.5 Resonant orbit families in the 66 391 Moshup system

不难发现，在不规则引力场模型下，无法得到严格的平面共振轨道，所有轨道在z方向都存在一定的偏移。对于远离主星的共振轨道，轨道z方向幅值相对较小，将其认为近平面共振轨道；而随着轨道距离主星逐渐接近，轨道z方向的偏移愈加明显，轨道呈现出明显的三维特征。另外图5中不同颜色反映了轨道具有不同大小的Jacobi常数，可以看出随着偏移量的逐渐增大，轨道的Jacobi常数越来越小，轨道能量逐渐增大。

3 稳定性分析与应用

稳定性是周期轨道的重要特性之一。稳定的共振轨道可以长时间保持相对平稳的运行，大幅降低轨道维持所需的燃料消耗，实现目标的长期持续观测；而不稳定的共振轨道则可以作为转移轨道的中间过渡弧段，为轨道设计提供更多可能性，也可以用于对目标进行更立体全面的绕飞。

本节将首先给出周期轨道稳定性与分岔的分析方法，并结合前面共振轨道族的计算，分析不同共振比轨道的稳定性，研究同一族共振轨道稳定性随参数的变化情况；接着将轨道的稳定性应用到轨道转移设计中，针对不稳定的近平面共振轨道，计算其稳定与不稳定流形，设计基于共振轨道流形的同宿转移轨道。

3.1 稳定性与分岔特性分析

研究周期轨道的稳定性[27]，需要引入单值矩阵的概念。单值矩阵M是一个6 × 6的矩阵，为状态转移矩阵Φ在一个轨道周期T的值，反映了轨道末状态对于轨道初状态的敏感情况，具体计算公式为

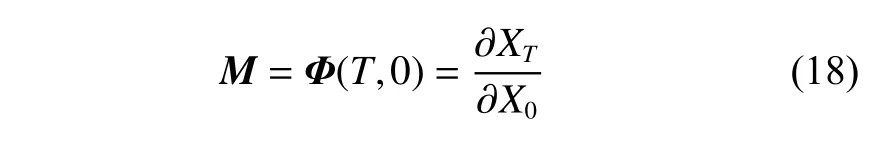
根据李雅普诺夫定理，单值矩阵的特征值总是成对出现，即若 λi是单值矩阵的一个特征值，则也是单值矩阵的一个特征值。单值矩阵有3对特征值，由于周期轨道s有一对恒为1的特征值，可以根据另外两对特征值来定量地判断周期轨道的稳定性。

给出稳定性指数ν 作为轨道稳定性的判定指标

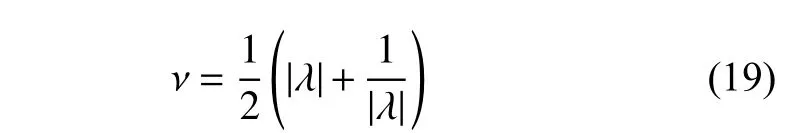
其中：λ为单值矩阵中模值最大的特征值。当ν=1时，周期轨道是稳定的；当ν>1时，周期轨道是不稳定的，此时轨道存在稳定与不稳定流形，可通过这一对模值不为1的特征值对应的特征向量方向计算。

在轨道族沿着某一个方向延拓的过程中，若对应轨道的空间结构发生显著改变，则此时轨道出现了分岔现象。分岔现象可以反映在特征值的变化上，即一对特征值在复平面上的某一点交汇，随后又沿另一个方向逐渐远离。可以根据特征值的不同变化将分岔分为多种类型，包括：正切分岔、倍周期分岔、第二Hopf分岔等，不同种类的分岔过程可能伴随着轨道稳定性的改变或新轨道族的产生[28-29]。

4组不同共振比轨道族包括稳定性指数在内的多项参数如表5所示。可以发现所有轨道的稳定性指数均大于1，轨道都是不稳定的；相较之下，1∶1共振轨道较为稳定，而其它共振轨道族的不稳定性都很强。

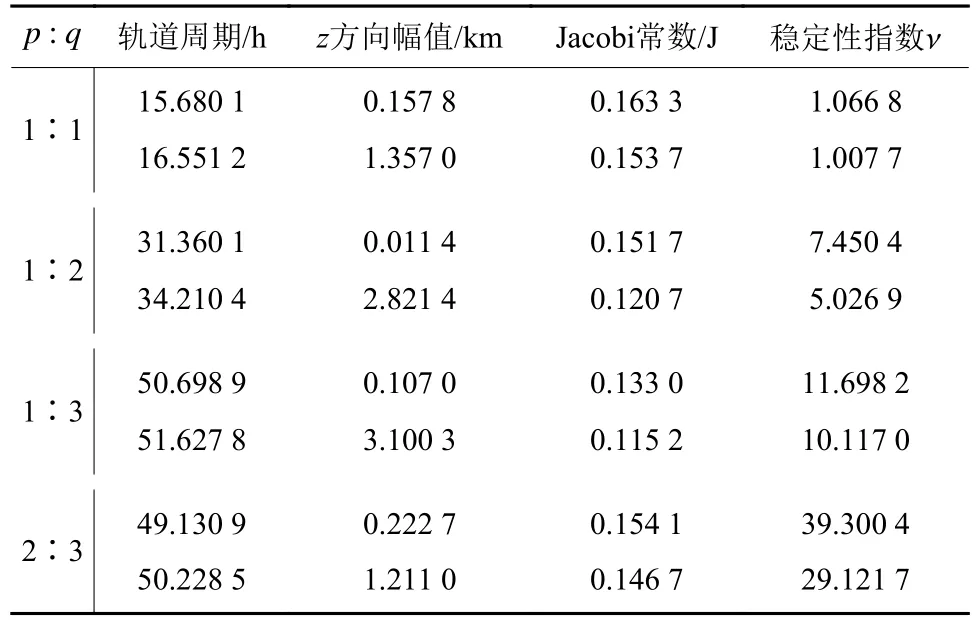
表5 共振轨道族的相关参数Table 5 Parameters of the resonant orbit families

以1∶1共振轨道族为例进行更大范围的延拓，可以得到更多种类的轨道族，如图6所示。分析轨道周期，轨道能量与轨道稳定性的关系，1∶1共振轨道族可以分为小周期轨道、中周期轨道和大周期轨道3组。其中小周期轨道对应于北向共振轨道族，其轨道周期随能量是单调变化的，且轨道的稳定性指数接近于1；中周期轨道对应南向共振轨道族和轴向共振轨道1族，两族轨道在空间上是连续的，但两者稳定阶数不同，南向共振轨道有一对大于1的特征值，轴向共振轨道1族有两对大于1的特征值；大周期轨道对应轴向共振轨道2族，在某个能量对应的轨道稳定阶数也发生改变，但并没有新的轨道族产生。

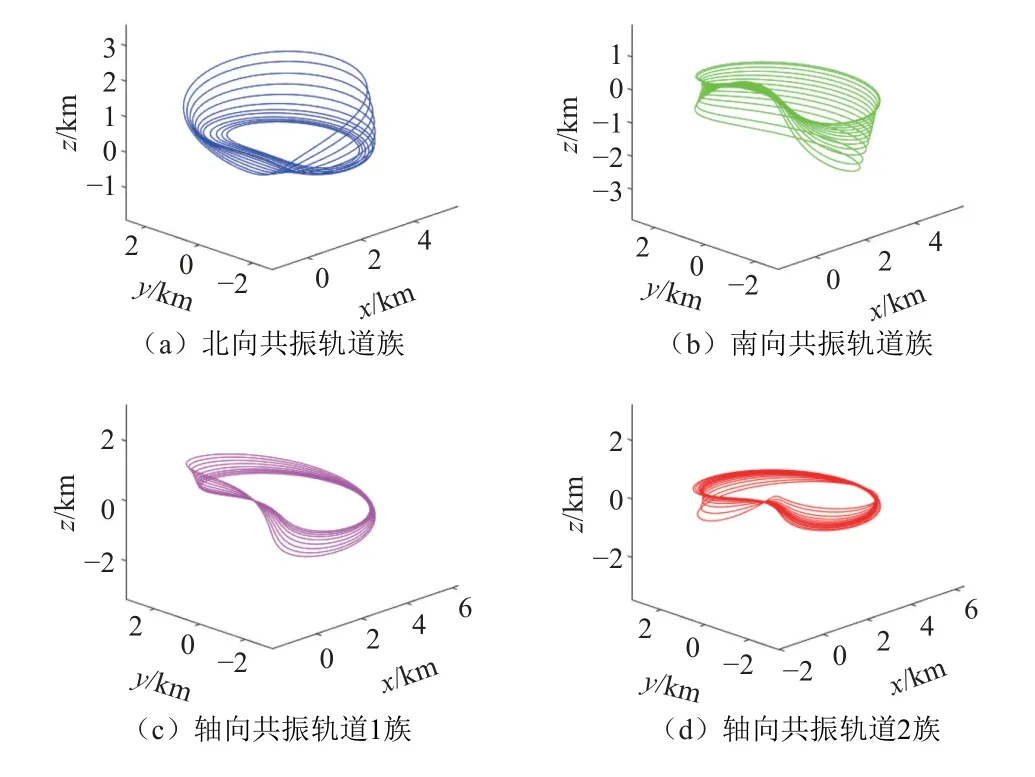
图6 大范围延拓的1∶1共振轨道族Fig.6 1∶1 resonant orbit families by wide-range continuation

双小行星系统不规则引力场中的共振轨道族可以类比球形主天体时经典圆型限制性三体问题的轨道族分岔。在经典圆型限制性三体问题中，可由平面共振轨道在两个分岔点处沿特定的特征向量方向延拓，分别分岔得到三维镜像共振轨道族和轴向共振轨道族，多种轨道族在分岔点处相连，在空间中是连续的，如图7（a）所示；而在不规则引力场中，3段周期范围不同的轨道可以直接选取轨道周期作为延拓参数通过单参数连续法得到，且轨道族在空间上不再连续，不同轨道族对应曲线没有交点，如图7（b）中所示。轨道族的不连续现象是由于小行星引力场的不对称性引起的特殊现象，在对称引力场模型中都不会出现[18,30]。

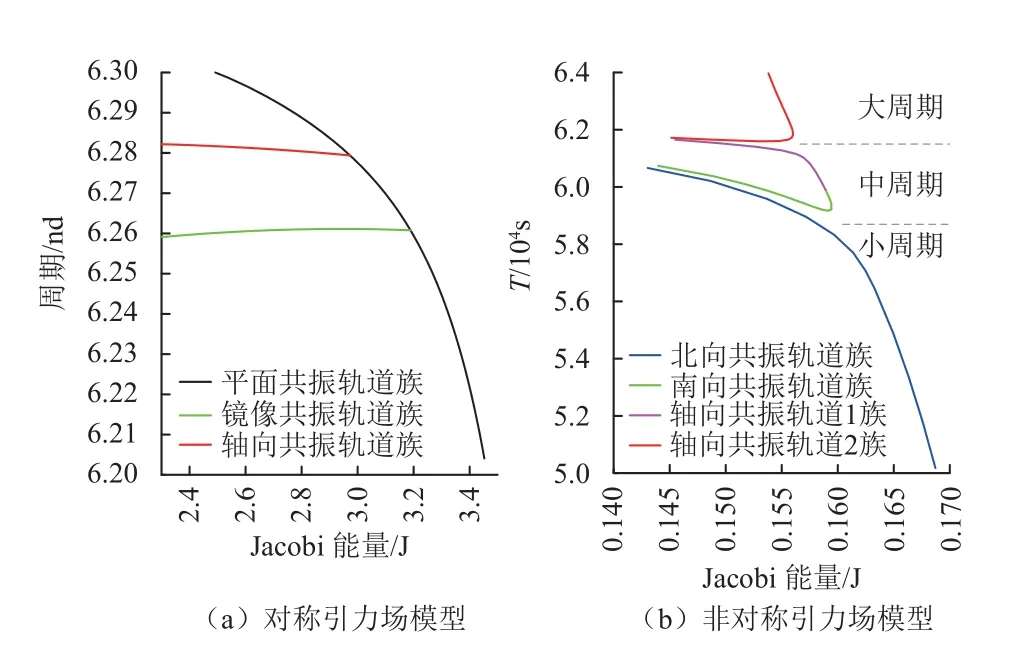
图7 共振轨道族分岔图Fig.7 A bifurcation diagram of resonant orbit families

进一步从稳定性的角度对几类轨道族进行分析，仿真结果如图8所示。可以发现整体上位于下半部分的北向与南向共振轨道相对稳定，而位于上半部分的轴向轨道具有较强的不稳定性。通过与轨道幅值进行对比，外侧包络线处的轨道都接近于平面轨道，轨道也相对稳定，而越远离外包络线轨道在z方向的幅值越大，南向北向共振轨道的稳定性指数逐渐减小，而轴向轨道的稳定性指数却逐渐增大，两类轨道在稳定性上呈现出相反的规律。

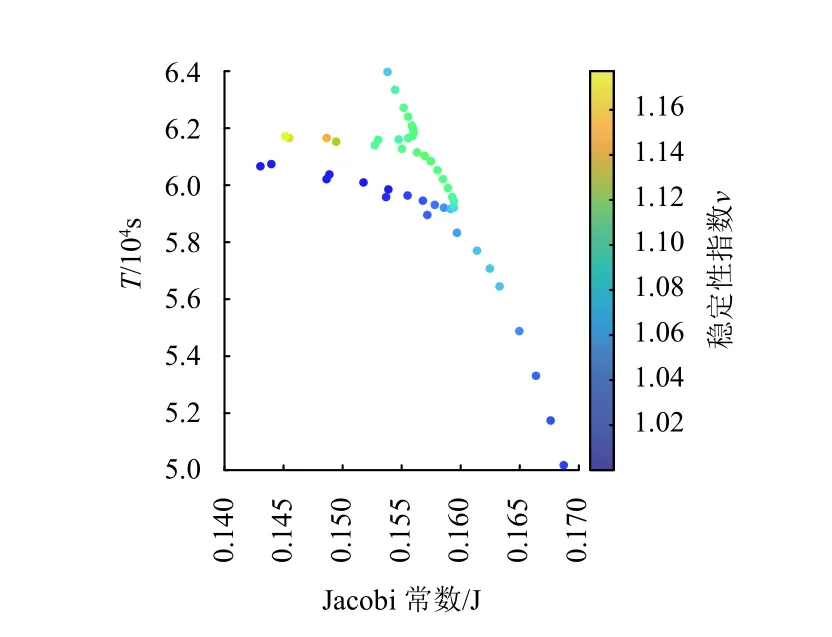
图8 共振轨道族分岔与稳定性分析Fig.8 The bifurcation diagram and stability analysis of resonant orbit families

3.2 共振轨道流形与同宿转移

利用不稳定共振轨道的流形可以进行轨道间的转移设计。目前这方面的研究集中在圆型限制性三体问题中，包括利用共振轨道实现不同平动点轨道间的转移、平动点轨道与环主从星轨道间的转移、共振轨道的同异宿转移[31]等。这里设计一种基于流形的双小行星系统附近共振轨道同宿转移方法，由于不对称引力场的引入，相对提高了轨道设计的精度，其它轨道间的转移可以类比本方法实现。

对同宿转移的轨道选择出于以下几点考虑：首先选择的轨道需要是不稳定的，且特征值相对较大比较好，这样在较小的积分时间内，流形就可以离开或靠近原始轨道；选择z方向幅值相对较小的轨道，这样可以在流形连接过程中暂时忽略z方向的位置和速度，方便采用庞加莱截面选择拼接点；另外由于双小行星系统距离相对较近，为避免与小行星发生碰撞，应尽可能选取距离主从星适中的轨道。在此选择1∶2近平面共振轨道进行同宿转移设计，流程如下：

1）计算共振轨道单值矩阵两个不等于1的特征值，确定稳定与不稳定流形的特征向量方向；

2）选择适当的扰动距离d，分别在特征向量方向上逆向和正向积分一定时间，得到轨道的稳定与不稳定流形；

3）由于共振轨道的空间流形相对杂乱，采用庞加莱截面法，选择y=0作为超平面，对计算的流形在x-坐标系上绘制庞加莱相图，如图9所示。

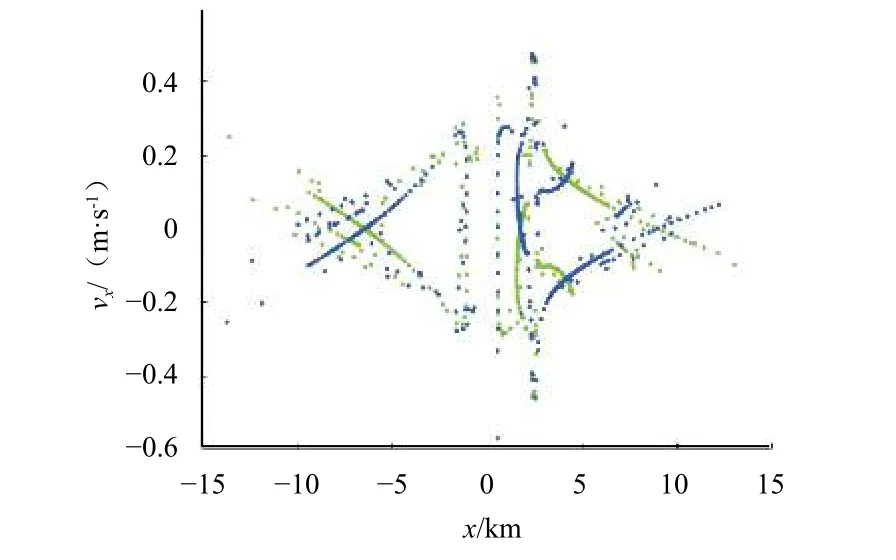
图9 稳定与不稳定流形的庞加莱相图Fig.9 Poincaré map for the stable and unstable manifolds

4）将稳定流形与不稳定流形在庞加莱相图上的交点作为拼接点，进行反向积分，可得到近似的同宿转移轨道；

5）为消除前面忽略z方向的影响，以近似同宿转移轨道为初值，在转移轨道初末状态与共振轨道满足一定连续性的约束条件下进行打靶法，最终得到完整的同宿转移轨道。

计算发现，由于引力场的不规则性，庞加莱相图也不再对称。同宿转移设计的初步仿真结果如图10所示，黑线表示双星系统的1∶2共振轨道，红线表示设计的转移轨道，星号点标注了转移轨道的起始与终止位置，整个转移过程大致需要101.497 h。

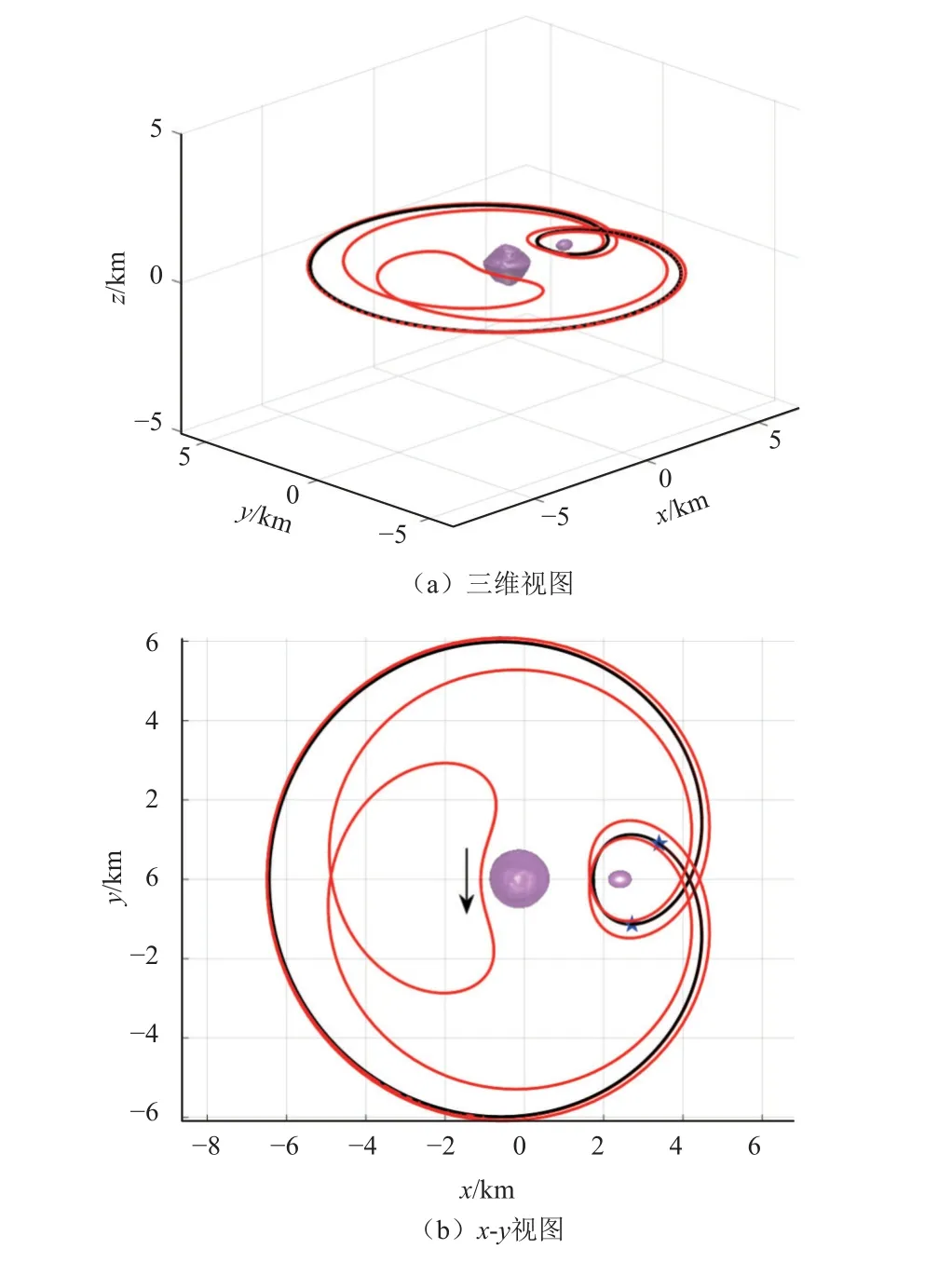
图10 1∶2共振轨道的同宿转移Fig.10 Homoclinic transfer between a 1∶2 resonant orbit

4 结论

本文基于多面体-椭球引力场模型研究了双小行星系统附近的共振轨道动力学问题。建立了双小行星系统附近的轨道动力学方程，分析了不规则引力场模型的影响，发现由于动力学环境不再具有对称性，与球形主天体时的经典圆型限制性三体问题相比，平动点在各个方向都发生了一定偏移；随后给出了共振轨道的设计方法，通过打靶法、同伦法并进行轨道延拓得到了一系列不同共振比的轨道族，计算结果表明轨道在z方向都存在幅值，且随z方向幅值的增大，轨道的能量逐渐增大；对轨道族进行稳定性分析，发现了不规则引力场模型中轨道族的不连续现象，并利用不稳定的共振轨道设计实现了基于流形的同宿转移，为小行星系统内的轨道转移设计提供了可行的思路。

本文尚未考虑主星快速自旋和从星引力场不规则性等影响因素，在实际任务设计中可以将本文的结果作为名义轨道；针对共振轨道近星点距离双星过近的问题，实际应用中可选择近拱点位于两星连线中间处的轨道以提高安全性；同时本文转移轨道的设计方法初步应用于近平面轨道，对于大范围的三维轨道转移有待后续进一步的研究。